电力系统自然频率特性系数区间预测方法

蒙永苹，张明媚，向明旭，杨渝璐，黄俊凯，杨知方

(1．国网重庆市电力公司，重庆市 400014；2．输配电装备及系统安全与新技术国家重点实验室(重庆大学电气工程学院)，重庆市 400044)

0 引 言

电力系统的安全、经济运行依赖于良好的频率质量，过高或过低的频率都将给整个系统带来严重危害[1]。自动发电控制(automatic generation control,AGC)系统是控制互联电网频率的重要手段。在AGC控制过程中，一般通过计算区域控制偏差(area control error,ACE)来确定系统有功调节量，我国电网ACE的计算周期一般为4 s[2]。AGC系统包含众多控制模式，不同控制模式具有不同的ACE计算方式。其中，联络线频率偏差控制是目前应用最为广泛的控制模式[3]。该模式的控制目标为将互联电网频率与联络线功率均控制在计划值附近。在该模式下，系数B是确定ACE的关键参数，其整定值决定了系统调整量对联络线功率偏差和频率偏差的偏向程度，将直接影响到频率控制性能的优劣。理想情况下，B系数整定值应与电力系统自然频率特性系数β相等，这样可使得互联电网中每个控制区的AGC仅负责本区域的负荷扰动[4]。当B系数略大于β系数时，系统有功调节量将大于系统功率偏差，可使得系统频率更快地恢复到计划值，但过大的B系数将使有功调节量及相关运行费用大幅增加。当B系数小于β系数时，将引起系统欠调甚至反调，危害系统频率质量。综上可见，B系数的整定原则是使其近似等于β系数，可略大于β系数，但应避免其小于β系数的情形。

目前，我国工业界主要采用固定系数法来整定B系数，即取B为年最大负荷的1%～2%，并每年调整一次[5]。而β系数受负荷波动、备用容量、机组启停方式等系统运行状态的影响，是非线性时刻变化的。因此，固定系数法难以满足B≈β，将引起系统的超调、欠调甚至反调。为使B系数更好地跟踪β系数，国内外学者提出了分段B系数整定法。文献[6]以系统频率偏差的大小为分段依据，提出了两段式B系数整定，以保障B>β。类似地，文献[4]将频率偏差量划分为了4个等级，当频率偏差量过大时，将增大B系数的整定值，以确保B>β。此外，文献[4]还根据系统运行方式建立了全天分时段B系数整定模型，使其更好地近似β系数。文献[7]根据火电、水电机组的一次调频死区设置情况，提出了三段式B系数整定方法。上述分段B系数整定法可在一定程度上缓解系统欠调、反调现象，但仍不能较好地满足B≈β。为更好地跟踪β系数的变化，有文献提出时变B系数整定方法，即通过实时在线计算β系数来整定B系数[8-9]。然而，该方法对数据的实时采集处理以及调度自动化水平提出了高要求。此外，由于β系数的在线计算需要在扰动发生后方可进行，故该方法控制时延较高，不利于频率的快速恢复。对此，文献[10]和[11]提出了β系数点预测方法，可根据系统功率扰动量对β系数的取值进行预测，为B系数的整定提供了参考。然而该方法仅考虑了功率扰动对β系数的影响，且预测误差的存在可能使得B<β的情况发生。

为更好地跟踪β系数的变化，并确保B略大于β，本文提出基于深度神经网络(deep neural network,DNN)与Bootstrap的β系数区间预测方法。该方法不仅能得到β系数的预测值，还可获得β系数的上下限，且完成DNN的训练后，所提方法可快速得到β系数的区间预测结果，能为下一个ACE计算周期中B系数的整定提供有力支撑。本文的主要贡献如下：

1)基于DNN建立了β系数点预测模型，该模型可计及系统功率扰动、备用容量以及机组启停方式对β系数的综合影响，实现β系数的准确预测；

2)在1)中所建预测模型的基础上，结合Bootstrap方法建立了β系数区间预测模型，可得到β系数预测结果的置信区间，为确保B略大于β提供了有力支撑。

1 基于深度神经网络的自然频率特性系数点预测模型

1.1 自然频率特性系数及其影响因素

电力系统自然频率特性是电网的固有特性，反映了稳定状态下系统有功功率和频率的关系，它包括负荷静态频率特性及发电机静态频率特性，常用自然频率特性系数β来表示，如式(1)所示[12]：

(1)

式中：β为系统自然频率特性系数；ΔP为系统功率偏差；Δf为系统频率偏差；KL、KG分别为负荷及发电机静态频率特性。

在电力系统运行过程中，β系数并非固定不变，它受系统功率扰动、备用容量、机组启停方式、负荷性质等因素的影响而表现出非线性和时变性[7，12]。由于负荷静态频率特性对β系数的影响较小，本文主要考虑了系统功率扰动、备用容量以及机组启停方式对β系数的影响。上述相关因素对β系数的影响如图1、表1和表2所示，相关数据由DIgSILENT/PowerFactory仿真软件生成。

由图1可见，随着功率扰动的增大，β系数也随之增大。但当扰动增大到一定程度后，发电机组的一次调频能力趋于饱和，β系数的变化曲线也趋于平缓[10]。

图1 自然频率特性系数随功率扰动的变化情况Fig.1 Variation of the natural frequency characteristic coefficient with the power disturbance

表1展示了系统功率扰动固定为80 MW，系统总备用容量为100 MW情况下，系统备用容量分配情况对β系数的影响。其中R表示机组预留备用容量，下标表示机组编号。由表1可见，具有备用容量的机组数量对β系数有着重要影响。当仅有1台机组具有备用容量时，其他机组由于满载，将不具备上调节能力，即满载机组的发电机静态频率特性为0[12]，因而此时β系数较小。随着具有备用容量的机组数量增多，将有更多机组具备调节能力，β系数随之增大。

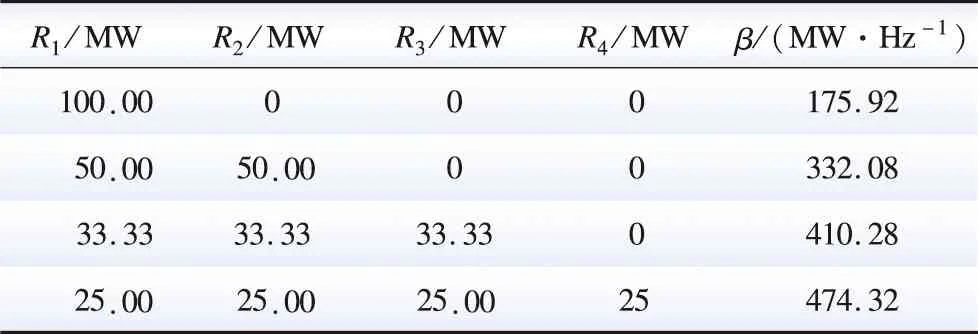
表1 系统备用容量分配情况对自然频率特性系数的影响Table 1 Impact of the system reserve allocation on the natural frequency characteristic coefficient

表2列出了固定功率扰动下(20 MW)，机组启停方式对自然频率特性系数的影响。由表2可见，当有机组停运时，由于在线机组所能提供的一次调频能力减弱，β系数将减小。且由于不同机组的一次调频能力存在差异，不同机组的停运将对β系数带来不同的影响。其中，机组1和机组2为同类型机组，故机组1或机组2停运时，β系数相同。机组3和机组4同理。

表2 机组启停方式对自然频率特性系数的影响Table 2 Impact of the unit commitment on the natural frequency characteristic coefficient

1.2 自然频率特性系数点预测模型

深度神经网络是传统浅层神经网络的拓展，它具有多隐藏层结构，具备强大的特征提取能力，可自动挖掘隐含在训练数据中的复杂非线性关系。近年来，随着深度学习技术的不断发展，DNN已被应用于电力系统中的各个领域，并取得了优异的效果[13-15]。在分析β系数影响因素的基础上，本节进一步利用DNN构建了β系数点预测模型，下面将对该模型进行介绍。

1.2.1特征向量选择

特征向量选择即确定DNN的输入向量及输出向量。本文构建DNN模型的目的在于实现β系数的预测。因此，DNN的输出即为实际的β系数。为实现β系数的准确预测，DNN的输入应为影响β系数的关键因素。由1.1节的分析可见，β系数的关键影响因素包括功率扰动量、各机组备用容量以及机组开机方式。其中，功率扰动量和各机组的备用容量可直接用相应的数值表示。对于机组开机方式，本文则采用0-1向量来表示，1表示机组运行，0表示机组停运。另外，需要说明的是，作为DNN输入的功率扰动量一般需要在扰动发生后才能获得。为提前预测未来某时刻β系数的取值，可采用该时刻功率扰动量的预测值作为DNN的输入。现有文献已提出基于极限学习机与集成学习的超短期功率扰动预测方法[16]。该文献的预测时段为4 s，与ACE的计算周期一致，预测结果的平均绝对百分比误差(mean absolute percentage error，MAPE)为3.42%，具有较高精度，可为本文所提β系数预测方法提供支撑[16]。此外，本文后续的仿真结果表明，完成DNN训练后，本文所提方法能在0.01 s内迅速得到β系数的预测结果。故借助预测时段为4 s的超短期功率扰动预测，本文所提方法能够为下一个ACE计算周期(4 s)中B系数的整定提供参考。仿真中也将验证所提方法对功率扰动预测误差的鲁棒性。

确定好特征向量后，便可收集相应数据，并形成训练样本用于DNN模型的训练。

1.2.2DNN模型

DNN的结构如图2所示。

DNN由输入层、多个隐藏层以及输出层构成。同时，层与层之间以全连接的方式连接在一起。层与层之间的数据传递公式如式(2)所示：

al=s(Wlal-1+bl)

(2)

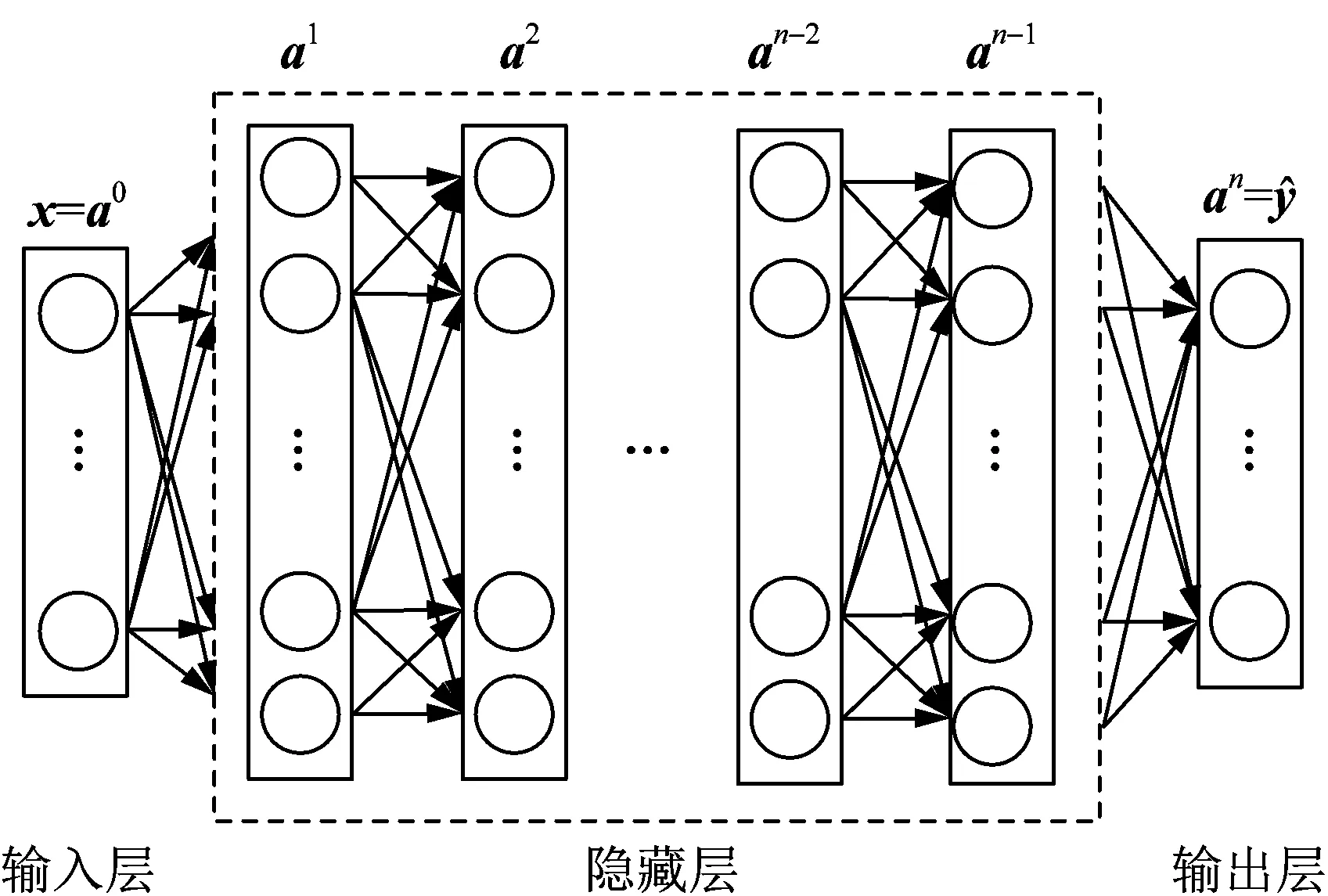
图2 DNN结构Fig.2 Structure of DNN

(3)

在隐藏层，本文选用带泄露线性整流(leaky rectified linear unit，LReLU)函数作为激活函数，可有效提高DNN模型的学习性能[17]，其表达式为：

s(z)=max(0.01z,z)

(4)

由式(4)可知，LReLU激活函数是一个分段函数，当输入值z小于或等于0时，输出值等于0.01z；当输入值z大于0时，输出值等于输入值z。

在输出层选用线性激活函数作为激活函数，其表达式如下：

s(z)=z

(5)

确定了DNN的基本框架后，便可通过训练样本对DNN进行训练。DNN的训练是利用有标签样本来调整参数θ={W,b}，使得损失函数L最小。其中θ指DNN训练所需要学习的参数，W为权重参数，b为偏置参数。本文选用的损失函数为均方差损失函数，如式(6)所示：

(6)

式中：m为样本数量；y为训练样本实际输出，即真实的β系数。

本文选用的训练算法为均方根传播算法，该算法的详细介绍参见文献[18]。训练完成后，便形成了基于DNN的自然频率特性系数点预测模型。

2 基于Bootstrap方法的自然频率特性系数区间预测模型

由第1节建立的自然频率特性系数点预测模型可预测得到β系数的取值，为B系数的整定提供参考依据。然而，该预测模型必然存在误差，若直接将B系数整定为β系数的预测值，则可能出现B<β这一不利于频率恢复的情况。为避免B<β的情况，本节进一步结合Bootstrap方法，建立了β系数的区间预测模型，能够得到在一定置信度下β系数的上下限。若将B系数整定为β系数的上限值，则可极大程度地避免B<β的情况发生。下面将对该区间预测模型进行介绍。

2.1 自然频率特性系数区间预测

对β系数的预测值而言，其误差包含两个部分：模型误差以及数据误差[19]。模型误差指模型训练效果不佳而引起的误差，引起训练效果不佳的因素包括训练过程中陷入局部最优、训练样本有限等。数据误差指因训练数据存在噪声等数据质量问题引起的误差。故存在误差的预测值可表示为：

(7)

式中：εm、εd分别为模型误差与数据误差。

本文假设模型误差与数据误差相互独立且服从期望值为0的正态分布：

(8)

现有文献已证明，即使误差的实际分布不服从正态分布，基于正态分布假设的误差分析仍可取得良好效果[20]。故本文关于误差服从正态分布的假设是合理可行的。

β系数的总预测误差ε为模型误差εm与数据误差εd的叠加，基于上述假设可知，总预测误差也服从期望为0的正态分布：

(9)

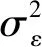
(10)

式中，Lα、Uα分别为置信水平为[100%×(1-α)]时，β系数的下限和上限。

2.2 Bootstrap方法及误差方差计算

本文采用Bootstrap方法来计算预测误差的方差。Bootstrap是一种重采样方法，其基本原理如下[21]：假设共有m个训练样本，采用有放回的方式从m个训练样本中进行抽样，抽样m次，便可得到一个新的包含m个训练样本的训练集，称为Bootstrap训练集。这样重复N次，便可得到N个Bootstrap训练集。通过每一个Bootstrap训练集都可以训练一个DNN模型，一共可得到N个DNN模型。通过N个训练好的DNN模型，可分别对模型误差与数据误差的方差进行计算。

2.2.1模型误差方差计算

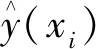
(11)

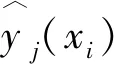
由此，可得到模型误差的方差为：

(12)

2.2.2数据误差方差计算

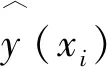
(13)

2.2.3总预测误差方差计算及β系数上下限

(14)

于是，由式(10)便可得到第i个样本对应的β系数上下限，如式(15)所示：

(15)

3 算例分析与讨论

为验证本文所提自然频率特性系数区间预测方法的有效性，本文利用DIgSILENT/PowerFactory仿真软件，通过调整自然频率特性系数的各影响因素共生成了653个样本。其中600个作为训练样本，余下53个用作测试样本。Bootstrap训练集个数N设为100，置信水平设定为95%。

本文将对比如下区间预测方法：

M1：基于DNN的Bootstrap方法，其中，DNN包含4个隐藏层，每层50个神经元；

M2：基于浅层反向传播(backpropagation，BP)神经网络的Bootstrap方法，其中，BP神经网络包含1个隐藏层，隐藏层神经元数为200[22]；

M3：基于极限学习机(extreme learning machine，ELM)的Bootstrap方法，其中，ELM包含1个隐藏层，隐藏层神经元数为200[23]。

本文所用计算机硬件环境为Intel(R)Core(TM)i7-7500U CPU @ 2.70 GHz 8 GB RAM。

3.1 自然频率特性系数区间预测准确性评价指标

为验证本文所提自然频率特性系数区间预测方法M1的有效性。本节将通过如下几个指标来衡量M1—M3的区间预测结果准确性。

β系数的点预测值可由式(11)得到，并用MAPE来衡量其点预测误差，如式(16)所示：

(16)

式中：IMAPE表示MAPE；mt为测试样本的个数。

所得预测区间是否有效涵盖了β系数的真实值由预测区间覆盖率(prediction interval coverage probability，PICP)来衡量，如式(17)、式(18)所示：

(17)

(18)

式中：IPICP表示PICP；ci用于判断第i个样本的实际值是否在预测区间内。

所得预测区间的宽度一般由平均预测区间宽度(mean prediction interval width，MPIW)来量化，如式(19)所示。为更直观展示预测区间宽度的大小，本文进一步定义相对平均预测区间宽度(relative mean prediction interval width，RMPIW)，如式(20)所示：

(19)

(20)

式中：IMPIW表示MPIW；IRMPIW表示RMPIW。

一般而言，较好的预测结果应具有较小的MAPE，较小的RMPIW以及较高的PICP。

3.2 不同方法自然频率特性系数区间预测性能对比

M1—M3所得区间预测结果对比如表3所示。由表3可见，在隐藏层神经元总数均相同的情况下，具有深层结构的M1能够取得最小的点预测误差，最小的相对平均预测区间宽度以及最高的预测区间覆盖率。其原因在于具有深层结构的DNN在特征提取方面的能力强于仅具有浅层结构的M2(采用BP浅层神经网络)及M3(采用ELM)，使得M1能更好地学习β系数的变化情况，取得更小的模型训练误差以及预测误差，进而得到更优的区间预测结果。此外，由表3可见，所提方法M1的平均单个样本预测耗时在0.01 s内，远小于ACE的计算周期(4 s)。故本文所提方法能够满足为下一个ACE计算周期中B系数整定提供参考所需的预测效率。通过将下一周期的B系数整定为β系数预测区间的上限，可有效避免B系数小于β系数的情况发生，确保系统频率控制性能。

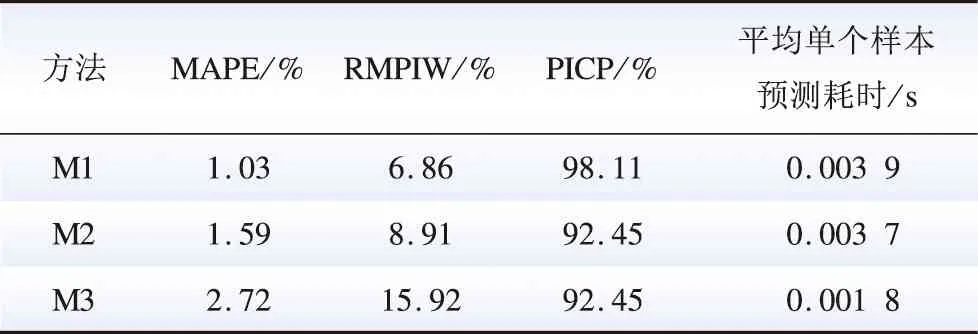
表3 区间预测结果对比Table 3 Comparison of interval prediction results

3.3 自然频率特性系数区间预测结果对功率扰动量预测误差的鲁棒性

如1.2.1节所述，本文所用特征向量包含系统功率扰动量。由于在功率扰动发生前，该扰动量是未知的，故在对β系数进行预测时，所用输入为功率扰动量的预测值。由于功率扰动量的预测存在误差，将预测值作为输入必然影响β系数区间预测的准确性。为验证本文所提区间预测方法M1对功率扰动量预测误差的鲁棒性，本节通过在真实功率扰动量的基础上添加服从正态分布的预测误差来生成功率扰动量的预测值，并测试了M1在不同功率扰动量误差情况下的预测效果，如表4所示。

表4 M1对功率扰动量预测误差的鲁棒性Table 4 Robustness of M1 to the forecast error of power disturbance %

由表4可见，随着功率扰动量预测误差的增大，β系数的预测准确性呈下降趋势。然而，在误差为1%～15%的范围内，本文所提方法M1仍能保持较高的预测准确性，β系数的点预测误差可保持在4%以内，相对平均预测区间宽度可保持在12%以内，预测区间覆盖率可保持在94%以上。由此可见，本文所提自然频率特性系数区间预测方法M1对于功率扰动量预测误差具备良好的鲁棒性，在现有功率扰动量预测精度的条件下(MAPE为3.42%)，所提方法的预测精度能够满足实际需求，可为B系数的整定提供参考。所提方法M1对于功率扰动量预测误差具备良好鲁棒性的原因可总结归纳为如下两点：1)由图1可见，功率扰动量的细微变化不会引起β系数的大幅变化。即使是在图中斜率最大处，10%的功率扰动量变化也仅会引起β系数1.2%的变化；2)训练样本输入中的功率扰动量也是预测值，通过学习训练，DNN对功率扰动量的预测误差具有一定适应性。此外，本文所采用的Bootstrap方法也可提高预测结果的鲁棒性[24]。

为进一步避免因所提方法预测结果不准确导致B系数的整定不合常理，可根据工程经验预先给B系数的整定值框定一个限制范围[Bp,γBp]，其中，Bp指电网目前实际的B系数整定值，γ为比例系数，可根据工程经验设定取值。仅当β系数的预测上限值在限制范围内时，才将B系数整定为预测上限值，否则将B系数整定为限制范围的上限或下限，从而确保B系数的整定值符合合理取值范围。

4 结 论

电力系统自然频率特性系数β随系统运行方式的变化而不断变化，这给AGC控制策略中频率偏差系数B的整定带来了困难。对此，本文在总结分析β系数主要影响因素的基础上，提出了基于DNN及Bootstrap的β系数区间预测方法。该方法可有效追踪β系数的变化情况，能够同时得到β系数的预测值及其置信区间。β系数的预测上限值可为B系数的整定提供参考，能有效避免B系数整定值小于β系数的情况发生。算例分析表明，本文所提区间预测方法能够取得良好的预测精度，且对功率扰动量预测误差具备良好的鲁棒性，验证了本文所提方法的有效性。