基于前馈自抗扰的光伏微电网混合储能控制策略

刘志坚，李晓磊，梁宁，郑峰，伍仰金，张婷婷

(1.昆明理工大学电力工程学院，昆明市 650504；2.福州大学电气工程与自动化学院，福州市 350108；3.国网福建省电力有限公司宁德供电公司，福建省宁德市 352101)

0 引 言

由于新能源发电技术存在间歇性、波动性和随机性，从而给系统带来了不平衡功率，故需要配备相应的储能控制技术保障系统的稳定性。近年来，国内外储能技术有了长足的进步，如蓄电池、超级电容、超导储能及混合储能设备都已经大量投入应用。双向DC-DC变换器是混合储能控制的关键，其控制性能决定了混合储能系统的控制性能。因此，双向DC-DC变换器的研究逐渐成为一个研究热点。

为了降低双向DC-DC的稳态误差，文献[1]提出了微分前馈的自抗扰控制策略，以实现减小逆变器稳态误差的目的。传统混合储能系统中存在电压偏差和分配精度[2]的问题，文献[3]采用基于一致性理论的分布式控制方法进行改进，以实现不同储能设备分频分配，并提高了直流母线电压的稳定性。文献[4]以混合储能系统(hybrid energy storage system，HESS)为研究对象，提出了一种分布式储能系统分层控制策略，动态调整各储能单元的输出功率，并降低了荷电状态(state of charge，SOC)差异。为了提高微网逆变器的抗扰性能和动态性能，文献[5]将线性自抗扰控制(linear active disturbance rejection control，LADRC)应用于微网逆变器的时频电压控制，具有良好的解耦性能和动态特性。多分布式能源混合微电网[6]须考虑SOC自均衡，有利于提高不同储能设备之间输出功率的均衡度，并延长储能单元的使用寿命。为提高蓄电池储能系统的动态响应速度和抗干扰能力，电流环[7]引入自抗扰控制方法，可提高储能系统的调节性能和抗干扰能力。自抗扰控制(active disturbance rejection control，ADRC)存在参数不容易整定的问题[8-10]，文献[11]提出了一种较为简单且易于实现的自抗扰控制器参数整定方法，简化了自抗扰控制器参数整定问题[12]，并总结出较为简单的参数整定规律。

混合储能系统单独采用自抗扰控制，难以有效补偿高低频分量[13]波动，采用改进的二阶低通滤波法对混合储能系统中的高低频分量进行补偿[14-16]，有利于降低蓄电池和超级电容的容量需求[17-18]。现阶段，涉及混合储能控制方面的研究较多，但结合低通滤波和前馈自抗扰控制的储能控制技术[19-20]仍具有较大的研究空间。

考虑到混合储能系统中存在储能设备间功率分配有效性差、抗干扰能力较弱及并网功率质量较差等问题，本文提出基于前馈自抗扰控制(feedforward linear active disturbance rejection control,FF-LADRC)的光伏微电网混合储能控制策略，以实现混合储能系统功率分频分配，并实现对光伏微电网进行协调控制。同时，对所提控制策略提出一种参数整定方法，有效降低控制器参数整定的难度，并对控制器进行频域稳定分析，从理论上证明所提控制策略的稳定性和有效性。通过MATLAB仿真试验进一步验证所提控制策略具有良好的动态响应速度、鲁棒性，并能精确控制系统以达到良好抑制扰动的效果。

1 双向DC-DC变换器数学模型

混合储能控制的关键是对蓄电池和超级电容双向DC-DC变换器的控制，故须对蓄电池和超级电容的双向DC-DC变换器分别进行建模。

1.1 蓄电池双向DC-DC变换器建模

1.1.1蓄电池boost电路模型

通过对蓄电池双向DC-DC变换器进行状态空间平均法和小信号建模，蓄电池在boost电路下的电流传递函数Gi-ba2(t)和电压传递函数Gv-ba2(t)分别为：

(1)

(2)

式中：V为直流母线电压；C1-ba为蓄电池侧的等效电容；Rdc-ba为直流母线侧的等效电阻；dboost-ba为蓄电池在boost电路下的占空比；IL为电流内环的实际电流信号；L为电感；C2-ba为蓄电池在直流母线侧的等效电容；Rb-ba为蓄电池侧的等效电阻。

1.1.2蓄电池buck电路模型

通过对蓄电池双向DC-DC变换器进行状态空间平均法和小信号建模，蓄电池在buck电路下的电流传递函数Gi-ba1(t)和电压传递函数Gv-ba1(t)分别为：

(3)

(4)

1.2 超级电容双向DC-DC变换器建模

1.2.1超级电容boost电路模型

通过对超级电容双向DC-DC变换器进行状态空间平均法和小信号建模，超级电容在boost电路下的电流传递函数Gi-sc2(t)和电压传递函数Gv-sc2(t)分别为：

(5)

(6)

式中：C1-sc为超级电容侧的等效电容；Rdc-sc为超级电容在boost电路下的直流母线侧等效电阻；dboost-sc为超级电容在boost电路下的占空比；C2-sc为超级电容在直流母线侧的等效电容；Rb-sc为超级电容侧的等效电阻。

1.2.2超级电容buck电路模型

通过对超级电容的双向DC-DC变换器进行状态空间平均法和小信号建模，超级电容在buck电路下的电流传递函数Gi-sc1(t)和电压传递函数Gv-sc1(t)分别为：

(7)

(8)

2 前馈自抗扰混合储能控制策略

为了提高混合储能设备中功率分配的有效性和降低直流母线电压偏差，本文提出基于前馈自抗扰的光伏微电网混合储能控制策略，在出现功率波动时，能够补偿不平衡功率，稳定直流母线电压，提高并网侧功率的稳定性。与此同时，本文所提控制策略充分利用超级电容和蓄电池的高低频特性，提高了混合储能系统的功率分配。其整体控制策略结构如图1所示。本文所提控制策略采用的是三环控制结构，包括电压环控制、蓄电池电流环控制以及超级电容电流环控制。电压环控制采用前馈自抗扰控制，并结合低通滤波将电流分量转化为高频分量的超级电容输出参考电流信号和低频分量的蓄电池输出参考电流信号，与此同时，在蓄电池电流环控制和超级电容电流环控制中分别引入线性自抗扰控制。该控制策略通过分别控制蓄电池和超级电容双向DC-DC变换器的电感电流，进而控制混合储能系统的充放电电流，可有效提高混合储能系统的动态响应速度和抗干扰能力。

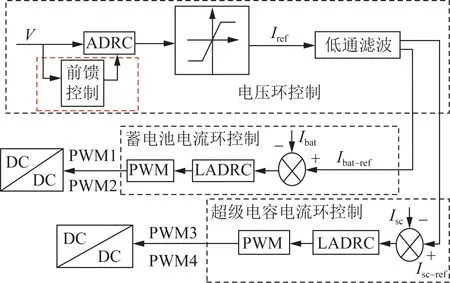
图1 混合储能控制策略整体结构Fig.1 Overall structure of a hybrid energy-storage control strategy

图中：Iref为电压环输出的电流信号；Ibat为蓄电池电流环控制中蓄电池电流的采样信号；Ibat-ref为蓄电池电流环控制中蓄电池电流的参考值信号；Isc为超级电容电流环控制中超级电容电流的采样信号；Isc-ref为超级电容电流环控制中超级电容电流的参考值信号。

蓄电池电流环控制中产生的占空比信号传送至脉冲宽度调制(pulse width modulation，PWM)产生器，产生PWM信号PWM1、PWM2来控制蓄电池电路中的开关S1、S2的开通与关断。超级电容电流环控制中产生的占空比信号，传送至PWM产生器，产生PWM信号PWM3、PWM4来控制蓄电池电路中的开关S3、S4的开通与关断。

2.1 前馈自抗扰电压环控制器

前馈自抗扰电压环控制器结构如图2所示。

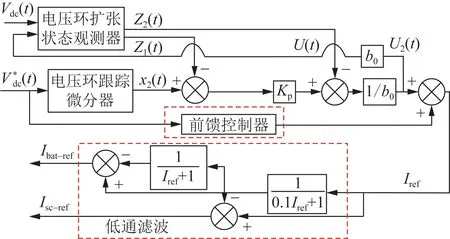
图2 前馈自抗扰电压环控制结构Fig.2 Feedforward of the voltage loop control structure of active disturbance rejection

2.1.1电压环跟踪微分器

x1(t+1)=x1(t)+λx2(t)

(9)

(10)

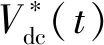
2.1.2电压环扩张状态观测器

电压环扩张状态观测器用来准确跟踪出实际电压信号V1(t)和电压环中实时估计的总扰动V2(t)。电压环扩张状态观测器的实现形式为：

E1(t)=V1(t)-U(t)

(11)

V1(t+1)=V2(t)-αV1E1(t)+b0Vdc(t)

(12)

V2(t+1)=-αV2×|E1(t)|1/2sign[E1(t)]

(13)

式中：αV1、αV2为状态观测器的增益参数，为提高状态变量和误差估计的准确性，故本次状态观测器的增益参数αV1、αV2分别设置为100、300。

2.1.3电压环线性反馈控制器

电压环线性反馈控制器对扩张状态观测器所估计的扰动进行线性化动态补偿。X2(t)为Vdc(t)经过跟踪微分器产生的微分信号，其和Z1(t)作差的误差信号将在电压环线性反馈控制器中生成控制量。其实现形式为：

(14)

2.1.4电压环前馈控制器

电压环前馈控制器是在电压环跟踪微分器输入信号位置引入一条正反馈通道，将采样电压信号和给定电压信号作差，通过前馈系数来抵消扰动信号，进而实现信号的无静差跟踪和扰动补偿，同时有利于降低混合储能控制系统的超调量和调节时间，进一步提高系统稳定性。其实现形式为：

(15)

式中：kqk为前馈系数，kqk=2。

2.1.5电压环低通滤波

为实现储能设备间的功率分频分配，采用电压环低通滤波。其功能是根据系统中功率的频率不同，将Iref进行高低频分量的划分，高频分量作为超级电容电流环输入电流参考值Isc-ref，低频分量作为蓄电池电流环输入电流参考值Ibat-ref，从而实现功率的分频分配。电压环低通滤波的实现形式为：

(16)

(17)

2.2 线性自抗扰蓄电池电流环控制器

蓄电池电流环采用改进线性自抗扰控制器，相比于传统自抗扰控制器，取消了跟踪微分器环节，这是由于蓄电池电流环需要快速跟踪指令变化，故不需要安排过渡环节。本次蓄电池电流环控制主要由两部分组成：线性扩张状态观测器和比例微分控制器。线性自抗扰蓄电池电流环控制结构如图3所示。

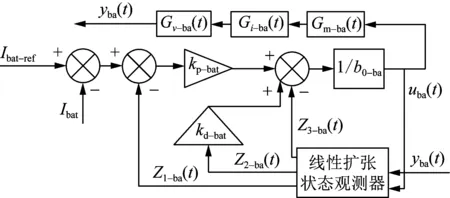
图3 线性自抗扰蓄电池电流环控制结构Fig.3 Current loop control structure of linear active disturbance rejection battery

2.2.1蓄电池电流环线性扩张状态观测器

本次蓄电池电流环中的线性扩张状态观测器提高了系统响应速度，并减小了超调量。根据输入uba(t)和输出yba(t)，准确估计系统的状态变量和作用于系统内外扰动之和。扩张状态观测器控制算法为：

(18)

式中：z=[z1-ba(t)，z2-ba(t)，z3-ba(t)]为系统状态及作用于系统内外扰动之和；L=[β1-ba，β2-ba，β3-ba]为本次状态观测器的增益矩阵；b0-ba为控制增益。

将式(18)进行转换，可得：

(19)

为实现蓄电池控制环中状态变量及总扰动的准确估计，须对β1-ba、β2-ba、β3-ba、b0-ba适当选择，并进行参数整定。

2.2.2蓄电池电流环比例微分控制器

在蓄电池电流环状态观测器扰动估计的基础上，比例微分控制器须构建出补偿反馈环节，对蓄电池电流环的扰动进行抑制，提高蓄电池电流环的抗扰能力。比例微分控制器通过补偿方式实现对扰动的抑制，增强蓄电池电流环的稳定性，使闭环系统获得较好的动态性能和稳态性能。本次比例微分控制算法为：

(20)

式中：kp-bat、kd-bat分别为蓄电池电流环的增益系数。要提高蓄电池电流环的稳定性，需要对kp-bat、kd-bat适当选择，并进行参数整定。

2.3 线性自抗扰超级电容电流环控制器

超级电容电流环的控制目标是平抑直流母线电压的波动，同时保持超级电容器端电压的一致。本次超级电容电流环控制主要由两部分组成：线性扩张状态观测器和比例反馈控制器，其结构如图4所示。

图4 线性自抗扰超级电容电流环控制结构Fig.4 Current loop control structure of linear active disturbance rejection supercapacitor

2.3.1超级电容电流环线性扩张状态观测器

本次超级电容电流环线性扩张状态观测器准确估计系统总扰动之和，提高了系统响应速度，并减小了超调量。

令z1-sc(t)-ysc(t)=e，并构造超级电容线性扩张状态观测器，如式(21)所示。

(21)

式中：z1-sc(t)、z2-sc(t)、z3-sc(t)分别为系统状态变量及作用于系统内外扰动；β1-sc、β2-sc、β3-sc为本次状态观测器的增益系数；b0-sc为控制增益。

为实现超级电容控制系统中总扰动的准确估计，须对β1-sc、β2-sc、β3-sc、b0-sc适当选择，并进行参数整定。

2.3.2超级电容电流环比例微分控制器

在超级电容电流环状态观测器扰动估计的基础上，系统须构建出补偿反馈环节，对系统扰动进行补偿，提高超级电容电流环的抗扰能力。比例微分控制器通过补偿方式实现对扰动的抑制，增强超级电容电流环的稳定性，使闭环系统获得较好的动态性能和稳态性能。

令Isc-ref-Isc=I，并构造比例微分控制规律如式(22)所示。

(22)

式中：kp-sc、kd-sc分别为蓄电池电流环中的增益系数。从式(22)可以看出，本文所提控制规律结合了比例反馈控制、输入微分前馈以及扰动补偿，具有优良的控制性能。

3 控制器参数整定及频域分析

下文以蓄电池电流环控制器为例进行参数整定和稳定性分析，超级电容电流环控制器同理。结合式(18)—(20)，可得出蓄电池电流环控制器的传递函数为：

(23)

(24)

仿真实验中，首先根据被控对象的数学模型对控制增益b0-ba进行估计，然后确定蓄电池电流环状态观测器的带宽ω0-ba和ω1-ba，采用逐渐增大的方式进行调参，进而分别确定β1-ba、β2-ba、β3-ba和kp-bat、kd-bat，通过不断调试，得到一组比较理想的控制器参数。本文所提参数整定方法较为简单且易于实现。

在控制器的频域特性分析过程中，ω0-ba分别取值为20、30、40、50、60时，频域分析特性曲线如图5所示。随着ω0-ba的增大，曲线在右移的过程中，相位滞后逐渐减小，蓄电池电流环控制器的误差估计收敛速度逐渐提高，动态响应速度逐渐提高。故实际工程应用中对ω0-ba的整定，可按照从小到大的趋势整定。但也需要注意ω0-ba的增大会放大噪声的问题，当噪声过大时，适当减小ω0-ba即可。

图5 ω0-ba变化下的频域特性曲线分析Fig.5 Frequency domain characteristic curve under ω0-ba change

在控制器的频域特性分析过程中，ω1-ba分别取值为156、160、170、180、190时，频域分析特性曲线如图6所示。随着ω1-ba的减小，曲线在右移的过程中，相位滞后逐渐减小，控制器的误差估计收敛速度逐渐提高，动态响应速度逐渐提高。故实际工程应用中对ω1-ba的整定，可按照从大到小的趋势整定。但也需要注意ω1-ba的增大会引起抖震的问题，此时，须增大ω1-ba来减小抖震。

b0-ba分别取5组不同的值，其频域特性分析线如图7所示。可以看出，当控制器参数β1-ba、β2-ba、β3-ba和kp-bat、kd-bat分别由ω0-ba和ω1-ba整定后，参数b0-ba对蓄电池电流环控制的变化具有良好的鲁棒性，有较好的控制性能。

图6 ω1-ba变化下的频域特性曲线分析Fig.6 Frequency domain characteristic curve under ω1-ba change

图7 b0-ba变化下的频域特性曲线分析Fig.7 Frequency domain characteristic curve under b0-ba change

4 仿真分析

为验证本文所提控制策略的正确性和有效性，在MATLAB中搭建了光伏微电网系统结构，仿真系统结构如图8所示。光伏微电网系统集成了光伏发电单元、超级电容储能单元、蓄电池储能单元、直流负载单元以及交流负载单元。光伏发电单元的额定容量为30 kV·A，蓄电池储能单元和超级电容储能单元的额定容量均为10 kV·A，直流负载单元和交流负载单元额定容量均为40 kV·A。为验证所提控制策略的有效性和可行性，本节将进行两组对比仿真实验，分别包括负荷阶跃变化下和阴影遮蔽下的仿真对比实验。

图8 光伏微电网混合储能系统结构Fig.8 Structure of hybrid energy storage system in photovoltaic microgrid

4.1 负荷阶跃变化下的仿真分析

本次仿真试验考虑负荷阶跃变化的情况，并将本文所提控制策略与LADRC、传统PI等控制策略进行对比，以验证所提控制策略的合理性。观察混合储能设备中各个储能设备的功率响应情况。在正常工况下，系统初始时刻接入第一组40 kW的交流负载。在1 s时，投入第二组40 kW的交流负载，2 s时切除。负荷阶跃变化下的仿真结果如图9所示。

图9(a)为混合储能系统中蓄电池和超级电容各自的功率输出曲线，即表示本文所提控制策略能够使混合储能中的超级电容模块在负载快速变化的瞬间进行快速响应，蓄电池能够响应稳态时的负荷，表明混合储能系统根据高低频分量的不同进而有效实现功率分配。图9(b)为不同控制策略下的蓄电池荷电状态(state of charge,SOC)变化趋势曲线。图9(c)表明混合储能中超级电容模块能够使其端电压在负载变化过程中始终保持一致，并且在功率波动后快速恢复到电压参考值，并且本文所提控制策略相较于传统PI、LADRC，有效降低了系统超调量和调节时间，具有更好的动态响应速度和抗干扰能力。从图9(d)可以看出，本文所提控制策略使得并网输出功率较为平滑，电能质量较高，相比于传统PI、LADRC等控制方法，具有较好的动态响应速度和调节能力。由图9(e)可知，负载变化时，直流母线电压发生抖动，但受到电压环的作用，很快恢复到电压参考值。

图9 负荷阶跃变化下的系统响应Fig.9 System response under load step change

4.2 光伏出力变化下的仿真分析

考虑到光伏发电随机性和波动性较大的特点，验证所提控制策略下储能设备的功率响应特性。图10为光伏出力变化下的光伏出力曲线及储能设备功率响应情况。

图10 光伏出力变化下的储能设备响应Fig.10 Response of energy storage devices under changes in photovoltaic output

由图10可以看出，在光伏出力波动较大的情况下，本文所提控制策略在能够对混合储能系统进行功率补偿，且蓄电池补偿功率频率较低，超级电容补偿功率频率较高，达到了控制蓄电池和超级电容功率的预期效果。

5 结 论

本文提出一种基于前馈自抗扰的光伏微电网混合储能控制策略，用于混合储能系统中不同储能设备的功率分频分配，同时提高并网侧功率的稳定性。对电流环控制器进行参数整定和稳定性分析，验证了所提控制策略的鲁棒性。与传统PI控制、LADRC的仿真对比表明，FF-LADRC具有更快的动态响应速度和抗负载扰动能力。同时，通过光伏出力变化下的仿真实验可以看出，FF-LADRC能够实现混合储能中储能设备功率的快速分频分配，其阶跃响应超调量较低，且对扰动具有良好的抑制效果。