混合型统一潮流控制器抑制风电次同步振荡控制策略

高本锋，王晓，梁纪峰，赵书强

(1.河北省分布式储能与微网重点实验室(华北电力大学),河北省保定市 071003；2.国网河北省电力有限公司电力科学研究院，石家庄市 050021)

0 引 言

输电线路装设串联补偿电容，可以大幅提高双馈风电场电能外送能力[1]。但是，双馈风机(doubly-fed induction generator，DFIG)控制系统与串补输电线路的相互作用，可能引发次同步振荡(sub-synchronous oscillation，SSO)问题[2]。

2009年10月，由于DFIG与串联补偿装置的相互作用，位于美国德州的一风电场发生系统SSO，导致大量风电机组脱网及撬棒电路损坏[3]。2012年12月底，我国华北某风电场也多次发生SSO事故[4]，研究表明，该SSO事故的发生是由于风机换流器与线路固定串补电容相互作用，引发系统发生次同步控制相互作用，最终使系统整体呈现负电阻特性。与传统火电机组SSO问题不同，DFIG经串补输电线路发生SSO的振荡频率与换流器控制系统、电气系统结构以及DFIG的出力有关[5]。而DFIG出力随机性和波动性很大，故其振荡频率具有显著的时变性[6]。因此，为增强系统稳定性，有必要研究在多种运行工况下DFIG经串补输电系统的SSO抑制方法。

目前，针对DFIG经串补输电系统SSO的抑制策略研究主要从风机侧[7-11]和电网侧[12-14]两方面开展，并取得了一些成果。在风机侧方面，抑制措施主要包括优化DFIG控制器参数[11]和附加阻尼控制[8-10]。文献[7]提出了一种减小转子侧换流器电流环比例系数的方法，以抑制DFIG经串补输电系统SSO；文献[8]通过在DFIG定子侧换流器控制策略中引入附加控制，从而产生一个与转速增量反相的附加转矩，为系统提供正阻尼，从而有效抑制DFIG经串补输电系统SSO。但大规模DFIG风电场中风机型号各异，须针对所有风机进行参数修改，工程量巨大。在电网侧装设柔性输电装置不仅可提高系统阻尼，实现DFIG经串补输电系统SSO的有效抑制[12-14]，而且可有效避免针对单台DFIG进行改造时工程量巨大的问题。文献[12]提出了一种应用静止同步串联补偿器抑制DFIG经串补输电系统SSO的方法，该方法可有效抑制DFIG经串补输电系统SSO。文献[13]通过改进统一潮流控制器(unified power flow controller,UPFC)的控制策略，以产生相应的次同步阻尼转矩，达到抑制DFIG经串补输电系统SSO的目的。文献[14]设计了一种针对UPFC的附加次同步阻尼控制器，该控制器采用模态分离控制结构，以实现多模态SSO抑制。但是，上述柔性输电装置由大容量电力电子器件构成，造价高昂，难以大规模推广应用。

混合型统一潮流控制器(hybrid unified power flow controller,HUPFC)由移相变压器(“Sen”transformer,ST)与UPFC串联构成，通过两者的优势互补，HUPFC可以实现与UPFC相同的控制功能。同时，由于ST通过变压器分接头和换向开关来控制潮流，为电磁型设备，故相比于UPFC，在达到同等容量的潮流控制下，HUPFC的造价更低，具有较好的应用前景[15-16]。从机理方面分析，HUPFC能够提供连续的补偿电压且灵活性较好，具备抑制SSO的条件。但是，目前尚未有文献开展HUPFC抑制SSO控制策略的研究。

本文提出一种HUPFC附加有源电阻控制(supplementary active resistance control,SARC)策略，以抑制DFIG经串补输电系统SSO。首先，阐述HUPFC的基本原理及其抑制DFIG经串补输电系统SSO的机理；然后，提出HUPFC的SARC策略，并给出SARC的参数整定方法；最后，在PSCAD/EMTDC环境中，以华北某风电场作为仿真算例，验证HUPFC附加有源电阻控制策略抑制DFIG经串补输电系统SSO的有效性。

1 HUPFC的基本原理

1.1 UPFC原理

UPFC结构如图1所示，UPFC由并联耦合变压器T1、串联耦合变压器T2和交-直-交变流器共同构成。其中，交-直-交变流器由VSC1和VSC2两个电压源型变流器(voltage sourced converter,VSC)组成，二者通过直流电容(C)实现解耦。VSC1经T1并联接入输电线路，VSC2经T2串联接入输电线路。

图1 UPFC结构Fig.1 Structure of UPFC

1.2 ST原理

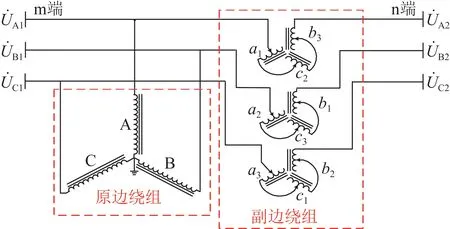
图2 ST结构Fig.2 Structure of a ST

(1)

1.3 HUPFC原理

HUPFC是由一个大容量的ST和一个小容量的UPFC串接构成，弥补了大容量UPFC成本高、损耗大以及ST离散调节的不足[17-18]。HUPFC的串联补偿电压向量如图3所示。

图3 两级调节时HUPFC补偿电压向量Fig.3 Compensation voltage vector of HUPFC when the number of taps is two

(2)

设ST的补偿电压最大值为UST，若ST级数为n，则其级电压为UST/n。由几何关系知，若要满足HUPFC无盲区补偿，UPFC的最小输出电压UUPFC为：

(3)

由于ST与UPFC串接接入线路中，通过ST与UPFC的电流相同，因此两者的容量之比为输出电压之比。从经济性考虑，在保证HUPFC无盲区补偿的前提下，所需UPFC的容量越小越好。此时ST与UPFC的容量之比满足：

(4)

2 HUPFC抑制DFIG经串补输电系统SSO原理

2.1 现场SSO事故

本文提出的HUPFC抑制系统SSO策略主要针对双馈风电场经串补输电系统的SSO问题。我国华北沽源地区已经发生了多起由于双馈风电场与固定串补作用而导致的系统SSO，给华北电网的安全稳定运行带来了极大的风险。

图4为2012年12月华北沽源系统中某风电场输出功率曲线，其详细标示了各次SSO发生的具体时间。由图4可知，2012年12月该风电场共发生7次SSO事故，因此，针对双馈风电场经串补输电系统的SSO抑制方法研究极为迫切。

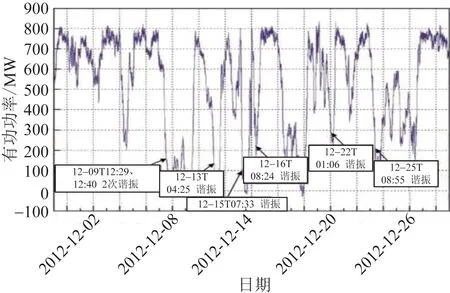
图4 某风电场输出功率曲线Fig.4 Output power curve of a wind farm

图5为华北沽源系统某次SSO事故时，该风电场输出有功功率的详细现场录波波形。从图中可以看出，从23:32:00起开始振荡，振荡大约持续了8 min，经历了部分风机脱网以及串补装置被旁路，SSO逐渐平息。

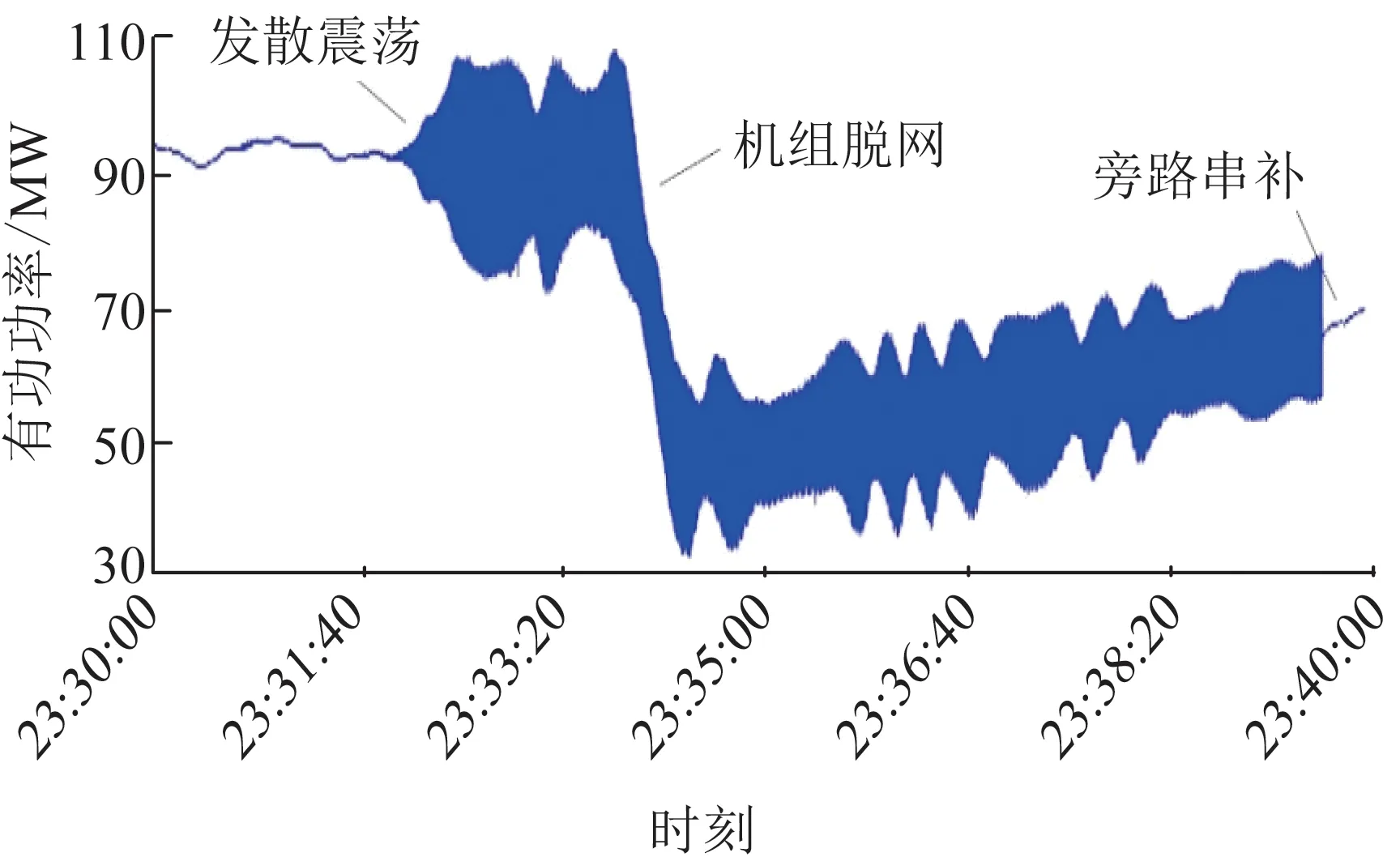
图5 某风电场输出有功功率Fig.5 Active power output of a wind farm

2.2 SSO发生机理

双馈风电场经串补输电系统SSO发生机理如图6所示。当系统受到小扰动后，电网侧产生频率为fsub的谐振电流，该谐振电流在转子上感应出相应的次同步电流。由于转子的旋转速度比次同步电流分量产生的次同步旋转磁场的转速高，故转差率为负值，致使转子的等效电阻变为负值。此时，转子等效电阻的绝对值大于谐振频率fsub下定子和输电系统的等效电阻之和，致使整个系统的等效电阻为负值，系统因缺乏正阻尼而振荡失稳[12]。

为了更加直观地阐述双馈风电场经串补输电系统SSO的发生机理，建立图6所示系统对应的等效电路，如图7所示。

忽略励磁电感Lm，将图7所示的系统等效电路进一步简化，得到图8所示的双馈风电场经串补输电系统简化等效电路。图中，s为转差率；uR为折算后的转子侧换流器输出电压；Req包括双馈风电场转子等效电阻(Rr+RRSC)、定子电阻Rs及输电线路电阻R；Leq包括转子漏感Lr、定子漏感Ls及输电线路电感L；C为线路串补电容；ωsub为次同步振荡角频率。

当图8中各电气参数满足式(5)所示的电气关系时，双馈风电场经串补输电系统将发生SSO。

(5)

由上述分析可知，当系统发生SSO时，通过增大谐振点处系统的等效电阻，使之大于0，进而为系统提供正阻尼作用，可以有效抑制系统SSO。

2.3 HUPFC抑制SSO原理

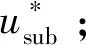
下面，通过详细的理论推导过程，进一步阐述HUPFC抑制DFIG经串补输电系统SSO的具体过程。

设线路电流iG中的次同步分量iG-sub频率为fsub，幅值为A，相位为φ，即：

iG-sub=Asin(ωsubt+φ)

(6)

图6 双馈经串补输电系统SSO发生机理Fig.6 Schematic diagram of SSO generation mechanism of DFIG-based wind farm connected to series compensated transmission system

图7 双馈风电场经串补输电系统等效电路Fig.7 Equivalent circuit of DFIG-based wind farm connected to series compensated transmission system

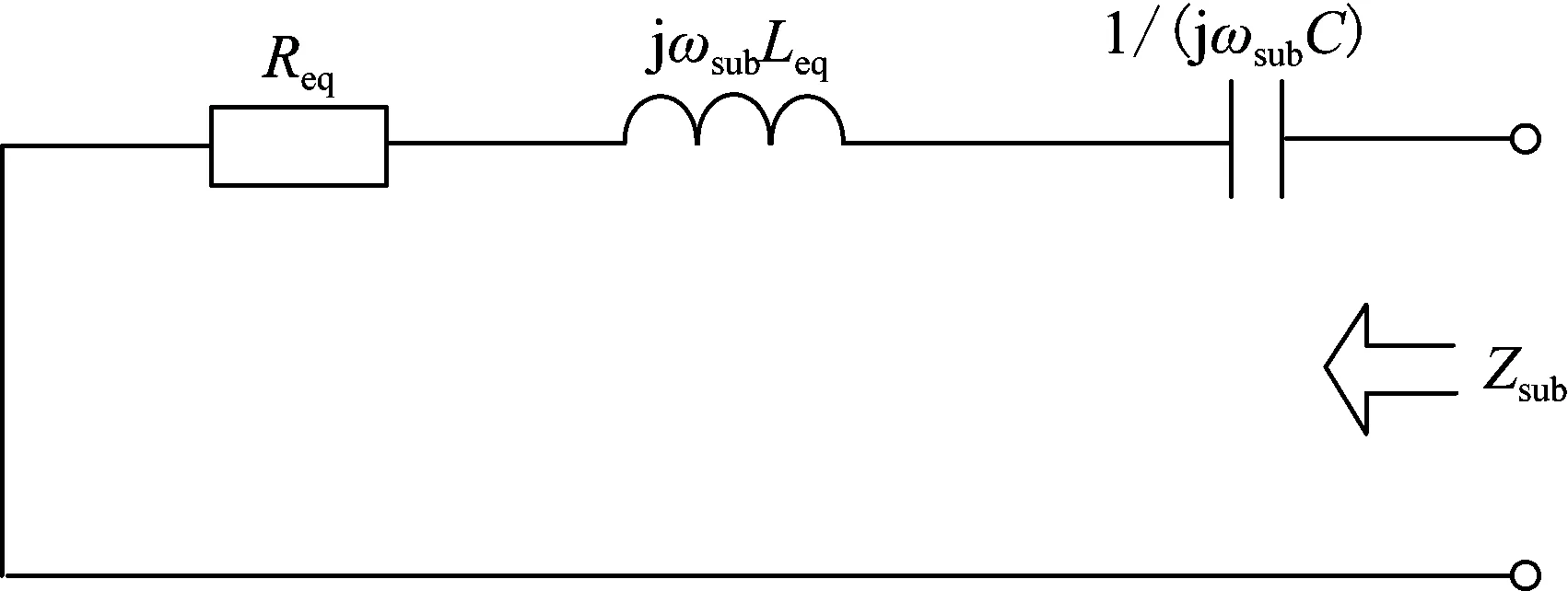
图8 双馈风电场经串补输电系统简化等效电路Fig.8 Simplified equivalent circuit of DFIG-based wind farm connected to series compensated transmission system

(7)

φ0+θ=φ

(8)

(9)

由于滤波环节对次同步电流的幅值影响特别小，近似认为As=A，即：

RHUPFC=k

(10)

此时，系统次同步振荡频率下的等效电阻Rsub为：

Rsub=Req+RHUPFC

(11)

增大k，可使RHUPFC增大，保证Rsub>0，从而抑制SSO。

若系统稳定，即A=0，则有：

(12)

可见，当系统发生SSO时，通过调整k，进而改变usub，使得系统等效电阻Rsub>0，即可实现对系统SSO的抑制。当系统稳定时，usub=0，不会影响系统和HUPFC装置的正常运行。

3 HUPFC抑制SSO控制策略

为抑制DFIG经串补输电系统SSO，提出HUPFC附加有源电阻控制策略。加入SARC的HUPFC控制系统结构如图10所示，HUPFC串联接入DFIG经串补输电系统220 kV输电线路中，用于调节线路潮流以及抑制系统SSO。

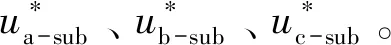
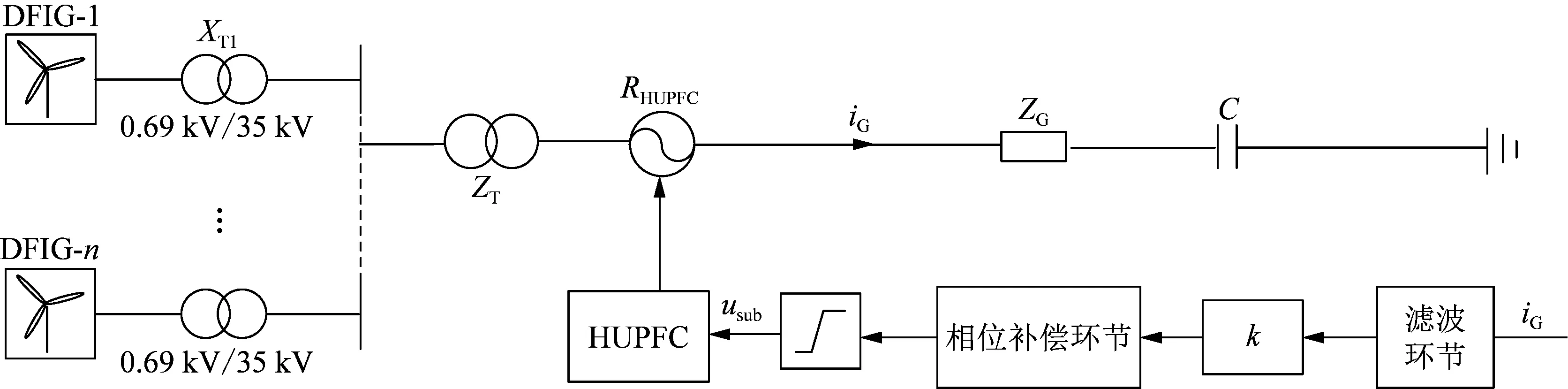
图9 HUPFC抑制SSO的原理Fig.9 The principle of HUPFC to suppress SSO

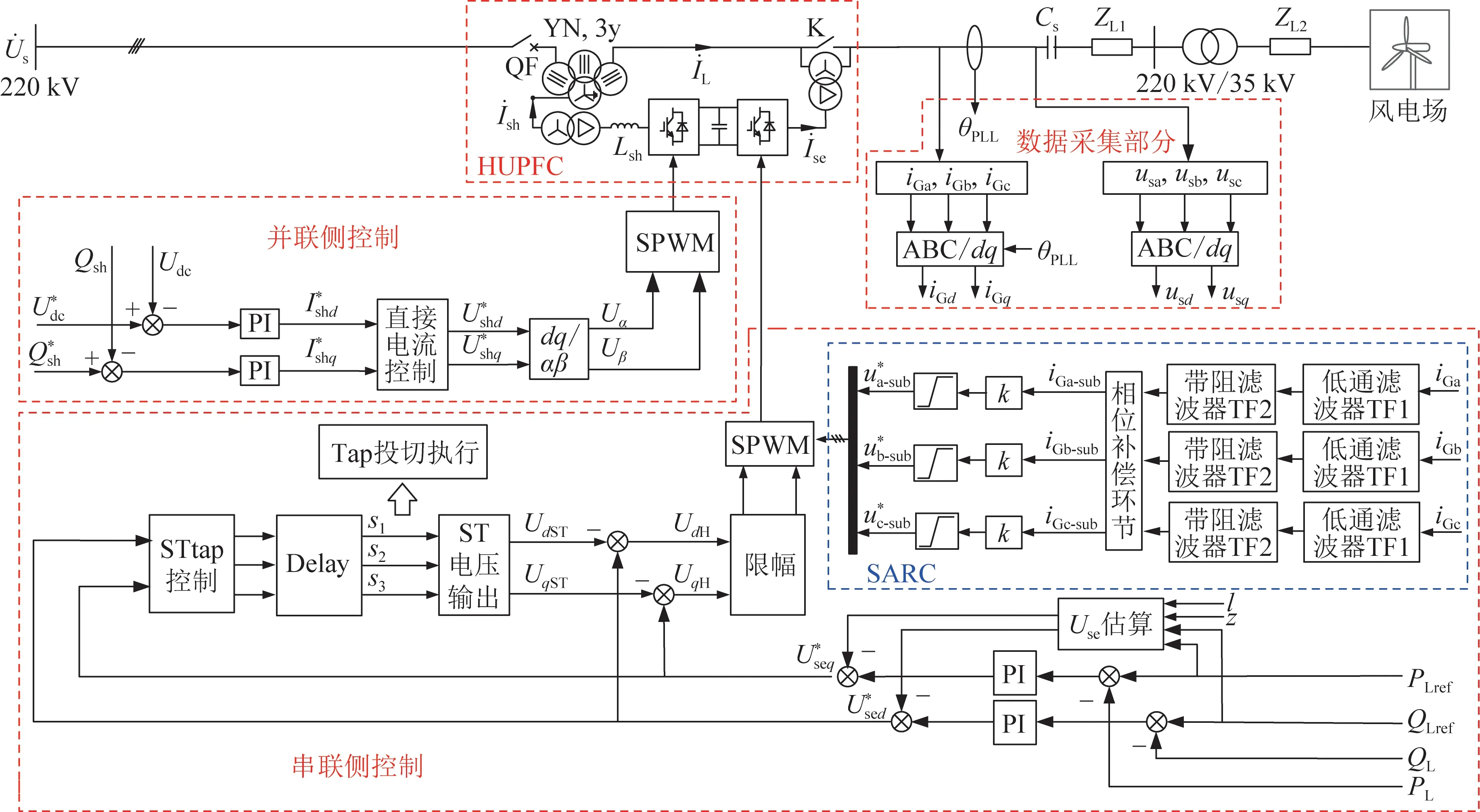
图10 加入SARC后的HUPFC整体控制策略Fig.10 Overall control strategy of HUPFC with SARC

SARC各环节的具体设计过程如下。

1)滤波环节。

如图10所示，滤波环节采用低通滤波器与带阻滤波器相组合的方式。低通滤波器的传递函数如式(13)中GTF1(s)所示；带阻滤波器的传递函数如式(13)中GTF2(s)所示。

(13)

式中：ωd为低通滤波器的截止角频率；ωc为带阻滤波器的中心角频率；ξ为阻尼系数，一般取ξ=0.7。

2)相位补偿环节。

次同步电流经过滤波环节会产生相位偏移，为减少滤波环节对次同步电流相位产生的影响，需要增加相位补偿环节。其传递函数Gp(s)为：

(14)

式中：Kp为补偿系数，保证补偿频率下次同步分量的幅值不变；τ为时间常数；λ为构造参数。

(15)

根据实际工程需求，对主要频率fm进行相位补偿，ωm=2πfm。Δθ为主要频率下经过滤波环节偏移的角度。

3)比例放大及限幅环节。

由式(10)可知，当DFIG经串补输电系统发生SSO时，Rsub=k。故可以通过增大比例放大环节中参数k，保证系统等效电阻大于0。k应在合理范围内取值，k值过小会造成SSO抑制效果不明显，k值过大会影响系统的稳定性。本文通过多次时域仿真，调整k在合理的范围内。限幅环节可以通过调整上、下限参数，保证线路电流不会超过热稳定极限值。

4 仿真验证

4.1 算例系统

基于华北某风电场实际运行参数，在PSCAD/EMTDC环境中，建立如图11所示的含HUPFC的双馈风电场经串补输电系统。如图11所示，风电场经变压器升压，并入串补度为30%、额定输送容量为130 MW的220 kV辐射型输电系统中。HUPFC串联接入220 kV输电线路，HUPFC详细参数见附表A1。

系统中，风电场由160台额定电压为0.69 kV、额定容量为1.5 MW的双馈风机构成，风机数量庞大，若对每台风机进行详细建模需要占用巨大的计算资源，普通计算机难以满足仿真需要。同时，研究表明，风电场发生SSO时，机组间的动态交互特性可以忽略，故可将整个风电场视作一个整体与外部电网相互作用[19-20]。文献[20]指出采用单机等值模型引起的等值误差在允许范围内，且次同步振荡特性与实际场景一致。因此，本文采用参数聚合法将整个双馈风电场等值为单台双馈风机，进而开展HUPFC抑制双馈风电场经串补输电系统SSO的相关研究。风电场等值参数的计算公式如式(16)所示，等值机的容量等于所有风机容量之和，其余参数采用容量加权的方式进行计算。

(16)

式中：n为等值风机的台数；下标eq表示等值之后的参数；j表示第j个风电机组的参数；S、T、Cp、C、r、H、D、K、Z分别为功率、转矩、风能利用系数、直流母线电容、叶轮半径、转动惯量、阻尼系数、扭转系数、阻抗；ρj为待聚合机组的额定容量与等值机组额定容量之比，即ρj=Sj/Seq。

双馈风电场经串补输电系统电磁暂态仿真模型中，电网侧一次系统结构与参数均与实际系统保持一致；等值机组各项参数计算过程中所用到的全部参数均为实际风电场实测数据；并且，等值机组控制系统结构与实际工程一致。双馈风电场经串补输电系统详细参数见附表A2。

4.2 SARC具体参数整定

1)滤波环节。

由式(13)可知，在滤波环节中需要整定的参数是ωd和ωc。ωd决定了低通滤波器允许通过的频率范围，考虑到衰减率的问题，取ωd为100 Hz；ωc决定了带阻滤波器能够阻断的中心频率大小，考虑到带宽对带阻滤波器阻断效果的影响，取ωc为50 Hz，带宽范围为49～51 Hz。在MATLAB环境中，对传递函数GTF1(s)、GTF2(s)进行计算，得：

(17)

2)相位补偿环节。

由式(14)可知，在相位补偿环节中需要整定的参数是Kp、λ、τ。当Δθ=-7°时，根据式(15)计算，得：

(18)

补偿前后的Bode曲线如图12所示。对于幅频特性，虽然补偿后幅值增益不再是1，但引起的偏差不足±0.8%，且在8 Hz下幅值增益仍为1。对于相频特性，补偿后8 Hz下对应的相位偏移为0°，且在4～10 Hz频率范围内相位偏移不足±2.5°，与未经相位补偿环节的相频特性相比，相位偏移情况得到明显的改善。在系统振荡频率范围下，HUPFC近似呈纯电阻特性。

图12 补偿前后Bode图对比Fig.12 Comparison of Bode diagrams before and after compensation

3)比例放大及限幅环节。

比例放大环节只有一个参数需要整定，即比例放大系数k。k越大，抑制效果越明显，但容易造成系统不稳定。本文根据多次仿真效果，确定k的取值为3。

限幅环节需要整定的参数是其上、下限值，需要根据线路电流的热稳定极限值来计算，同时留有一定的热稳定裕度。

4.3 仿真验证

分别改变线路负载度、串补度、ST与UPFC的容量配比，以验证HUPFC抑制DFIG经串补输电系统SSO的有效性。3 s时，投入串联补偿电容，待系统稳定后利用频率扫描法分析有、无SARC投入时DFIG经串补输电系统等值阻抗，并结合相应的时域仿真分析验证HUPFC附加SARC策略抑制系统SSO的有效性。

4.3.1线路负载度变化

为对线路负载情况进行有效的量化，定义负载度η为：

(19)

式中：Pa为线路实际传输有功功率；PN为线路额定传输有功功率。

在220 kV线路串补度相同，ST与UPFC的容量配比相同情况下，分别改变HUPFC目标潮流值，以使线路处于轻载(η=40%)与重载(η=80%)2种运行工况。3 s时投入串联补偿电容，待系统稳定后，运用频率扫描法分别计算出有、无SARC投入时，DFIG经串补输电系统在次同步频率4～10 Hz范围内的等效阻抗，如图13所示。

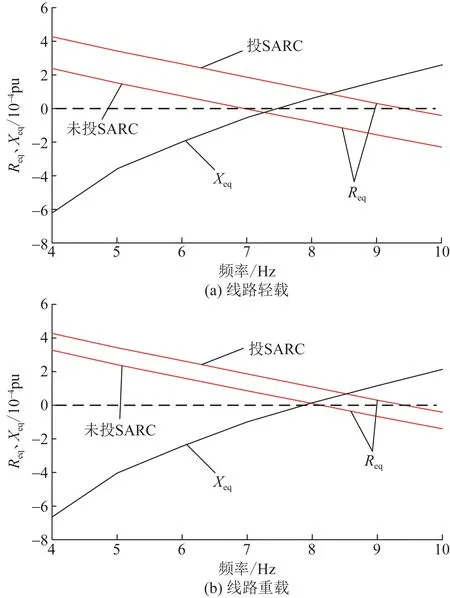
图13 不同线路负载度下，有、无SARC时系统等效阻抗Fig.13 Equivalent impedance of the system with or without SARC under different line load

由图13(a)可知，在线路轻载、Xeq=0 pu对应的振荡频率下，未投SARC时，Req为负。投入SARC时，系统等效电阻大于0，避免系统SSO的发生。由图13(b)可知，在线路重载、Xeq=0 pu对应的振荡频率下，投入SARC增大了Req，且无论是否投入SARC，系统等效电阻均大于0。

为了验证上述分析结果，分别针对上述2种工况，通过时域仿真，分析SARC投入前后，DFIG经串补输电系统输电线路传输有功功率情况。图14为2种工况下，SARC投入前后，输电线路传输有功功率P变化曲线。

由图14(a)可知，线路轻载且未投入SARC时，系统发生振荡，且幅值不断增大，系统最终失稳。快速傅立叶变换(fast Fourier transform,FFT)分析结果表明，系统失稳对应振荡频率为43 Hz，该振荡为SSO。而投入SARC时，有功功率SSO得到有效抑制，系统未失去稳定。由于线路有功功率的振荡频率与系统振荡频率互补[12]，故上述分析与频率扫描结果一致。由图14(b)可知，线路重载时，无论有、无SARC投入，系统均维持稳定。

图14 线路负载度不同，有、无SARC时线路有功功率Fig.14 Active power with or without SARC under different line load

实际上，有功功率即代表了捕获的风功率。风速越大，捕获的风功率越大，系统发生SSO的风险越低。上述仿真结果表明，线路负载度不同时，HUPFC均具有抑制SSO的效果。

4.3.2串补度变化

在HUPFC所在线路轻载运行，ST与UPFC的容量占比相同时，分别令220 kV线路的串补度为30%和50%。3 s时投入串联补偿电容，2种线路串补度下，有、无SARC投入时，线路有功功率P的变化曲线如图15所示。

由图15(a)可知，串补度为30%且未投入SARC时，系统发生振荡，且幅值快速增大，系统最终失稳。FFT分析结果表明，系统失稳对应振荡频率为41 Hz，该振荡为SSO。而投入SARC时，有功功率SSO得到有效抑制，系统未失去稳定。由图15(b)可知，串补度为50%且未投入SARC时，系统发生振荡，且幅值比串补度为30%时增大得更剧烈，系统最终失稳。FFT分析结果表明，系统失稳对应振荡频率为40 Hz，该振荡为SSO。而投入SARC时，有功功率SSO得到有效抑制，系统未失去稳定。上述仿真结果表明，在不同的串补度下，HUPFC均具有抑制SSO的效果。

图15 不同串补度下，有、无SARC投入时线路有功功率Fig.15 Line active power with or without SARC under different series compensated levels

4.3.3ST与UPFC的容量配比变化

由式(4)可知，在满足ST与UPFC最优容量分配的前提下，通过改变ST的调节级数可以改变ST与UPFC的容量配比(SST∶SUPFC)。当ST的调节级数为2时，ST与UPFC的容量配比约为3.5∶1；当ST的调节级数为4时，ST与UPFC的容量配比约为7∶1。

在HUPFC所在线路轻载运行，220 kV线路的串补度相同时，分别选取ST与UPFC的容量配比为3.5∶1和7∶1这2种工况。3 s时投入串联补偿电容，待系统稳定后，运用频率扫描法分别计算出有、无SARC投入时系统在次同步频率4～10 Hz范围内的等效阻抗，如图16所示。

由图16可知，不同容量配比下，投入SARC均增大了系统等效电阻Req。当SST∶SUPFC=3.5∶1时，增大的Req的数量级为10-3；当SST∶SUPFC=7∶1时，增大的Req的数量级为10-4。由此可知，ST与UPFC的容量配比越小，增大的Req越大，HUPFC的SSO抑制效果越显著。

为了验证上述分析结果，分别针对上述2种工况，通过时域仿真，分析了SARC投入前后，DFIG经串补输电系统输电线路传输有功功率情况。图17为2种工况下，SARC投入前后，输电线路传输有功功率P变化曲线。

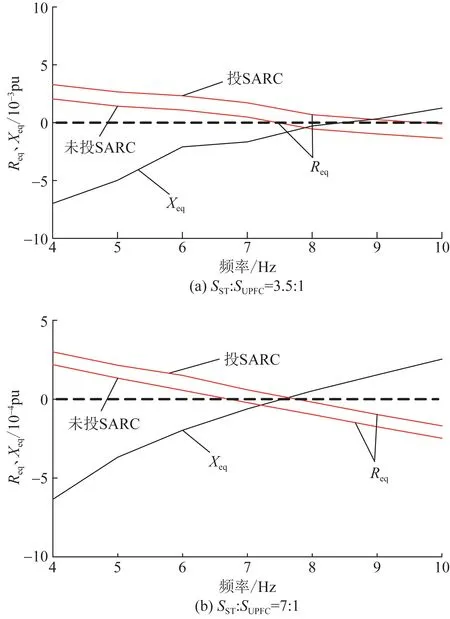
图16 不同容量配比下，有、无SARC时系统等效阻抗Fig.16 System equivalent impedance with or without SARC under different capacity ratios

图17 不同容量配比下，有、无SARC时线路有功功率Fig.17 Active power with or without SARC under different capacity ratios

由图17(a)可知，SST∶SUPFC=3.5∶1且未投入SARC时，系统发生振荡，幅值不断增大，系统最终失稳。FFT分析结果表明，系统失稳对应振荡频率为42 Hz，该振荡为SSO。而投入SARC时，系统在经历短暂振荡之后，有功功率SSO得到有效抑制，系统最终可以重新稳定。由图17(b)可知，当SST∶SUPFC=7∶1且未投入SARC时，系统发生振荡，幅值持续增大，系统最终失稳。FFT分析结果表明，系统失稳对应振荡频率为43 Hz，该振荡为SSO。而投入SARC时，系统发生等幅振荡，且振荡幅值与未投入SARC相比较小。上述仿真结果表明，在SST∶SUPFC不同时，HUPFC均具有抑制SSO的效果。

4.3.4线路故障类型变化

为验证HUPFC在不同故障类型下SSO抑制的有效性。HUPFC所在线路轻载运行，220 kV线路串补度相同，ST与UPFC容量配比相同。仿真开始前，串补电容设为投入状态，待系统稳定后，1 s时，在35 kV/220 kV升压变高压侧分别设置A相接地故障、AB相间短路、三相接地故障3种不同故障类型，故障持续时间为50 ms。检验不同故障类型下有、无SARC投入对SSO的抑制效果。不同工况下，有、无SARC投入时线路有功功率P的变化曲线如图18所示。

由图18可知，未投入SARC时，当系统发生不同类型故障后，有功功率均出现剧烈振荡，0.5 s后，出现等幅振荡，系统失稳。而当投入SARC时，当系统发生不同类型故障后，在SARC作用下，有功功率振荡均能在2 s后趋于稳定。上述分析结果表明，不同类型故障下，HUPFC均可以较好地抑制DFIG经串补输电系统SSO。

图18 不同故障类型下，有、无SARC时线路有功功率Fig.18 Active power with or without SARC under different fault types

5 结 论

本文针对DFIG经串补输电系统SSO问题，提出了一种HUPFC附加有源电阻控制策略。首先，分析了DFIG经串补输电系统SSO形成机理，系统等效电阻为负是激发系统SSO的原因。然后，基于SSO形成机理，提出了利用HUPFC产生正电阻的SARC策略。通过向输电线路叠加与线路中次同步电流相位相同、幅值可变的次同步电压，以增大系统等效电阻，从而抑制DFIG经串补输电系统SSO。最后，给出了SARC参数整定方法，以华北某风电场为仿真算例，采用频率扫描及时域仿真，验证了该策略抑制DFIG经串补输电系统SSO的有效性。本文提出的HUPFC附加有源电阻控制策略结构简单、参数整定简便，适用于工程应用。