多向大变位伸缩装置力学性能研究

钟明，赵彦龙，李轩

(西安中交土木科技有限公司，陕西 西安 710075)

1 引言

机荷高速公路作为横跨深圳东西方向的交通大动脉，车流量巨大，目前日均交通量达到12万～16万标准车。为缓解交通压力，深圳市拟在机荷高速公路原线之上架设高架桥。为避免拟建高架桥在后期运营时频繁更换支座，影响交通顺畅，拟建高架桥将采用墩梁固结结构。

采用墩梁固结结构的桥梁，整体结构承受外力或内力作用时，梁体变位均由伸缩装置实现，这对桥梁伸缩装置性能提出了更高的要求。

经分析得出，机荷拟建高架桥相邻梁体联端承受图1(a)所示不均匀荷载时，两联之间产生23 mm竖向剪刀错位[图1(b)]。目前中国主要使用的桥梁伸缩装置根据结构形式分为模数式伸缩装置、梳齿板式伸缩装置、橡胶式伸缩装置和异型钢单缝式伸缩装置4类。对于以上4种伸缩装置的小规格型号 (D160型)，规范仅要求竖向变位不小于15 mm，现有的伸缩装置无法满足小缝竖向23 mm的大变位要求。

为解决此问题，该文提出一种多向大变位伸缩装置设计方案，装置结构如图2所示。该多向大变位伸缩装置由活动齿板、固定齿板、支承横梁、变位箱体组成，其中活动齿板与支承横梁通过防松螺栓组件连接。

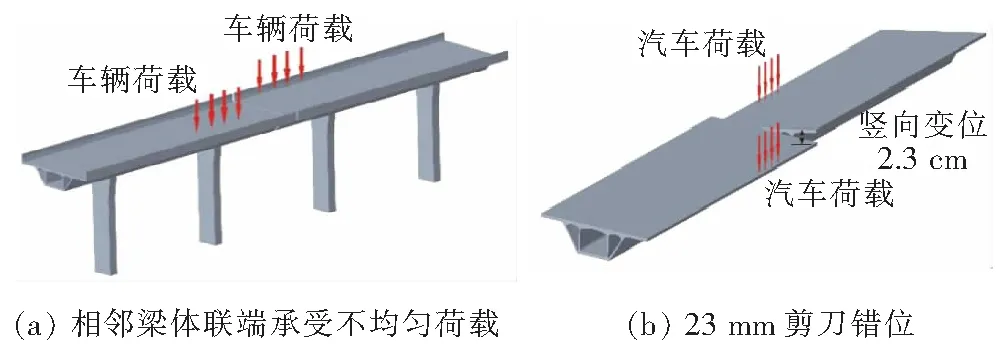
图1 桥梁联端剪刀错位

图2 多向大变位降噪型伸缩装置

变位箱内支承横梁上下方设有可自由转动的承压变位支承及弹性支承，当梁体发生竖向变位时，支承横梁可在桥梁纵向发生转动，同时带动活动齿板一起自由转动(图3)。伸缩装置被压缩至最小状态时，两侧承压变位支承间距为360 mm，承压变位转动0.07 rad即可满足竖向23 mm的变位要求。同时，通过精确设计活动齿板梳齿形状及尺寸(坡度、厚度)，能够实现齿端无上翘，可以保证伸缩装置表面的平整性和连续性，能够避免扎胎，提高行车安全性，并降低车辆通行噪声。此伸缩装置采用模块化设计，并且活动齿板与固定齿板采用螺栓连接，伸缩装置后期维修更换时，不需要对伸缩装置整幅进行更换，仅需对局部损坏部位进行维修更换，能够有效节约成本，同时最大程度减少对行车的干扰。

图3 伸缩装置变位功能示意图

要实现伸缩装置小规格(D160型)23 mm以上竖向大变位的目标，该文提出多向大变位伸缩装置以实现梁体转动与伸缩装置顺桥向伸缩的功能分离。该文首先对伸缩装置变位结构进行系统设计，然后结合有限元方法对此装置在静力荷载和动力荷载作用下的力学性能进行分析研究。

2 伸缩装置静力分析

2.1 伸缩装置有限元模型

多向大变位伸缩装置中活动齿板、固定齿板、支承横梁、变位箱等部件均采用Q355钢；承压变位支承及弹性支承中滑板采用聚四氟乙烯材料；连接螺栓采用40Cr(淬火)，10.9级高强螺栓。具体材料参数如表1、2所示。

表1 材料参数

表2 橡胶材料参数

多向大变位伸缩装置采用模块化设计，各节段间具有较强的独立性，因此该文选择单节段作为研究对象，并主要针对两种不同齿形的伸缩装置进行力学性能分析。两种型号伸缩装置除齿板外，其余部件均保持一致，且两种齿形齿板质量均为228 kg，如图4所示。

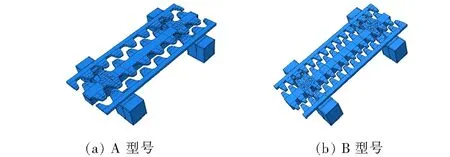
图4 不同齿形多向大变位降噪型伸缩装置

使用Solid Works建立伸缩装置三维模型后，将三维模型导入Abaqus中进行网格划分，生成有限元模型。伸缩装置有限元模型中各部件均采用缩减积分C3D8R单元进行划分，该单元在承受弯曲荷载时不会出现剪力自锁现象，并且能够应对复杂的接触问题，能够较为真实地模拟伸缩装置的受力情况。装置各部件接触通过基于罚函数的通用接触算法定义。根据伸缩装置实际工作状态，变位箱体外侧自由度全部约束，固定齿板与桥梁固结部分自由度全部约束。

2.2 静力荷载

根据JTG D60—2015《公路桥涵设计通用规范》中对车辆荷载的规定：车辆后轴重力标准值为140 kN，轴距为1.4 m，轮距为1.8 m，车轮着地面积为200 mm×600 mm。D160型多向大变位伸缩装置单节段长1.5 m，最大开启状态宽度为580 mm，可以确定仅有单轴单侧轮胎荷载作用于装置上。结合车轮着地面积及齿板尺寸，该文取表3所示两种代表工况分别对A、B型号伸缩装置进行分析，荷载作用位置如图5所示。

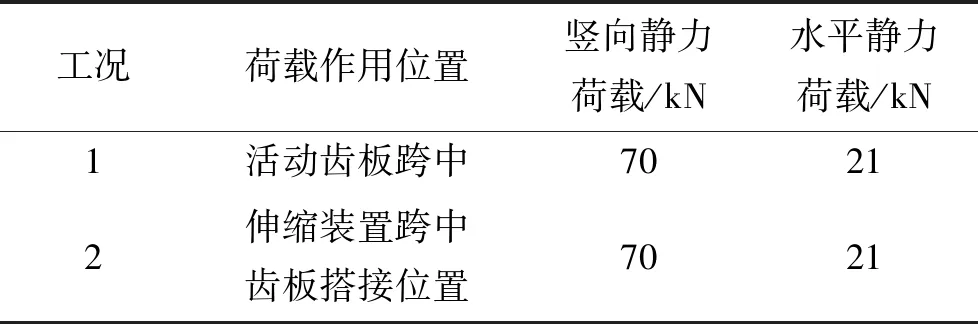
表3 荷载作用工况

图5 荷载作用位置示意图

2.3 计算结果分析

多向大变位伸缩装置中活动齿板、固定齿板、支承横梁、连接螺栓为主要强度控制元件，仅需对以上元件计算结果进行分析讨论。

(1)工况1静力计算结果

图6、7分别为两种型号伸缩装置梳齿板在工况1静力荷载作用下的Mises应力分布结果和位移结果。

图6 工况1荷载作用下齿板Mises应力分布图(单位：MPa)

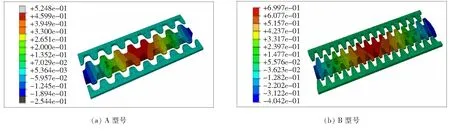
图7 工况1荷载作用下齿板位移计算结果(单位：mm)

从图6、7可以看出：A、B型号齿板在工况1荷载作用下最大Mises应力分别为92.97、93.96 MPa，均远小于屈服强度355 MPa；最大位移分别为0.524 8、0.699 7 mm，满足伸缩装置刚度要求；两种型号齿板最大Mises应力均出现在活动齿板跨中顶面齿间位置。

图8、9分别为两种型号伸缩装置支承横梁在工况1静力荷载作用下的Mises应力分布及位移结果。

从图8、9可以看出：A、B型号伸缩装置支承横梁在工况1荷载作用下最大Mises应力分别为48.47、46.76 MPa，结构未发生塑性变形；最大位移分别为0.158 3、0.232 4 mm，满足伸缩装置刚度要求；支承横梁在荷载作用下耳板与梁体连接拐角处以及螺栓孔位置有一定的应力集中，最大Mises应力出现在这两处。

图10为两种型号伸缩装置连接螺栓在工况1静力荷载作用下的Mises应力分布结果。

从图10可以看出：螺栓在弯剪组合作用下最大Mises应力出现在活动齿板与支承横梁接触截面；A型号伸缩装置螺栓最大Mises应力小于B型号，分别为64.85、72.63 MPa，这是由于工况1荷载作用下A型号伸缩装置齿板变形小于B型号齿板，连接螺栓所承受弯曲作用也相对较小导致的。

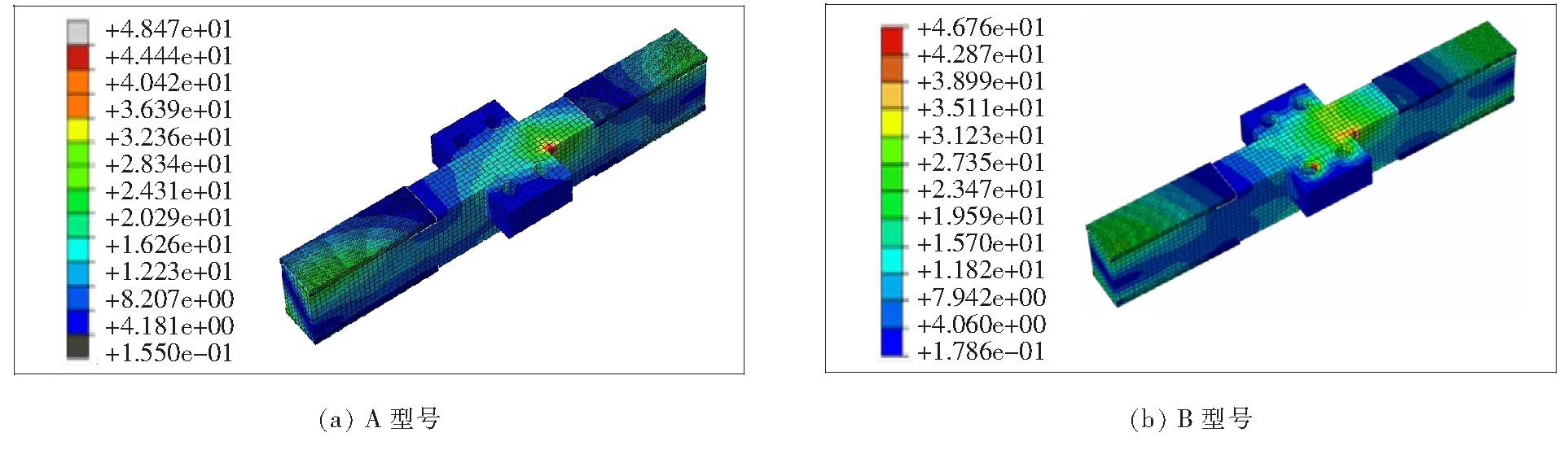
图8 工况1荷载作用下支承横梁Mises应力分布图(单位：MPa)

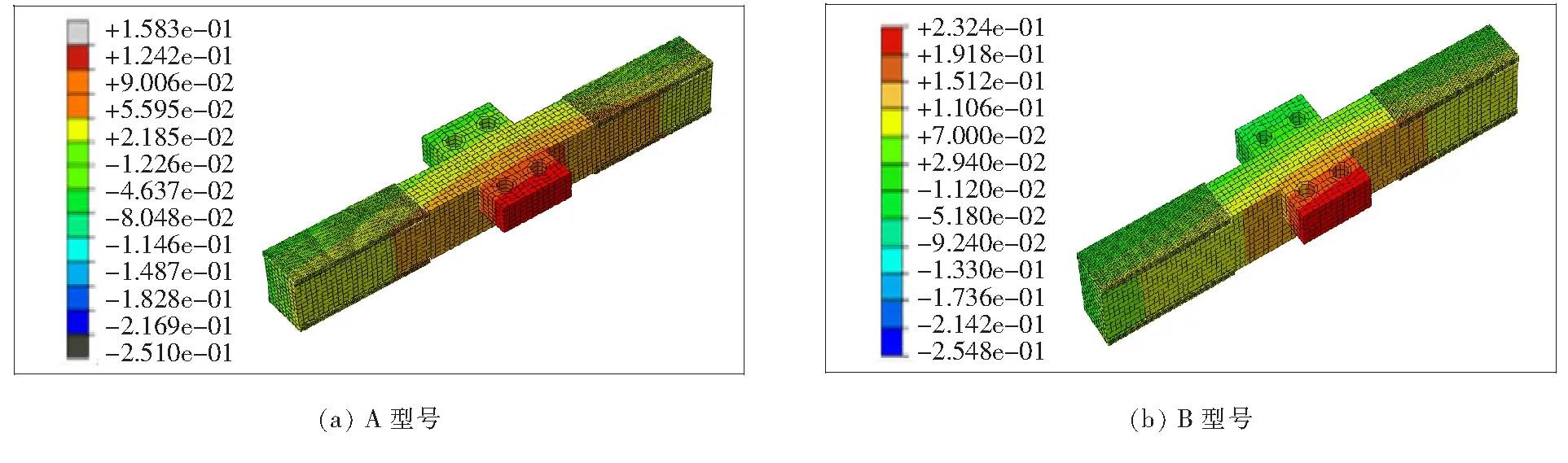
图9 工况1荷载作用下支承横梁位移计算结果(单位：mm)

图10 工况1荷载作用下螺栓Mises应力分布图(单位：MPa)

(2)工况2静力计算结果

工况2车轮荷载作用在齿板搭接位置，图11、12分别为两种型号伸缩装置梳齿板在工况2静力荷载作用下的Mises应力分布及和位移结果。

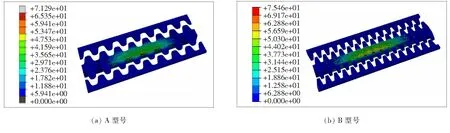
图11 工况2荷载作用下齿板Mises应力分布图(单位：MPa)

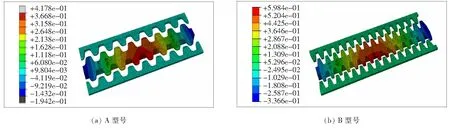
图12 工况2荷载作用下齿板位移计算结果(单位：mm)

从图11、12可以看出：A、B型号齿板在工况2荷载作用下最大Mises应力分别为71.29、75.46 MPa，均小于工况1荷载作用下的最大Mises应力值；最大位移分别为0.417 8、0.699 7 mm，满足伸缩装置刚度要求。

图13、14分别为两种型号伸缩装置支承横梁在工况2静力荷载作用下的Mises应力分布及位移结果。

从图13、14可以看出：A、B型号伸缩装置支承横梁在工况2荷载作用下最大Mises应力分别为28.03、37.85 MPa，支承横梁具有很高的安全系数；最大位移分别为0.123 4、0.178 5 mm，满足伸缩装置刚度要求。

图15为两种型号伸缩装置连接螺栓在工况2静力荷载作用下的Mises应力分布结果。

从图15可以看出：工况2荷载作用下两种型号伸缩装置螺栓最大Mises应力分别为34.93、57.33 MPa，远小于屈服强度900 MPa。

图13 工况2荷载作用下支承横梁Mises应力分布图(单位：MPa)

图14 工况2荷载作用下支承横梁位移计算结果(单位：mm)

图15 工况2荷载作用下螺栓Mises应力分布图(单位：MPa)

3 伸缩装置动力分析

为研究车辆通过多向大变位伸缩装置时引起的动力响应，对车辆后轴单侧轮胎分别以20、40、60、80 km/h的行驶速度通过多向大变位伸缩装置单节段进行动力仿真分析。

图16为齿板最大竖向位移与车辆行驶速度关系折线图，图17为齿板竖向振动加速度幅值与车辆行驶速度关系折线图。

从图16、17可以看出：随着车速的增加，活动齿板所产生的最大竖向位移及竖向振动加速度幅值均增加；相同速度下，轮胎经过A型伸缩装置时活动齿板最大竖向位移及竖向振动加速度幅值均小于B型伸缩装置。

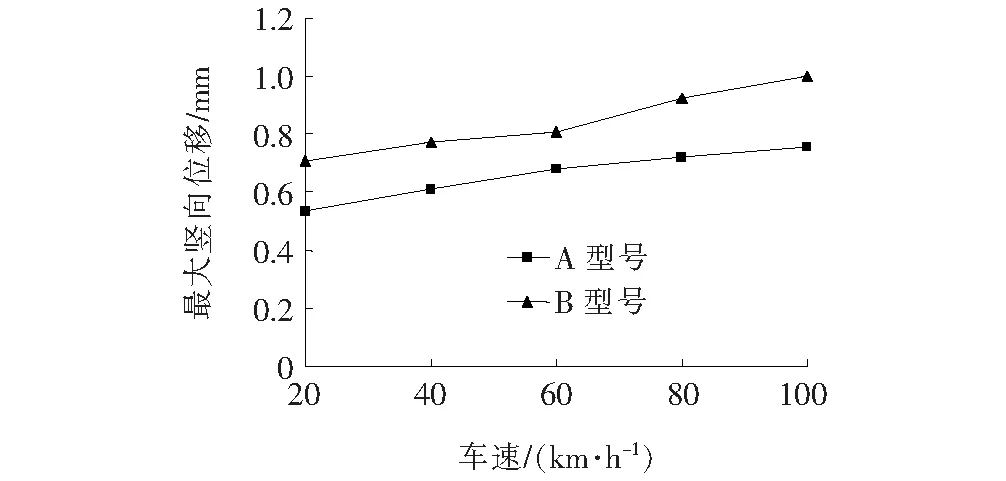
图16 齿板竖向最大位移-车速关系曲线

图17 齿板竖向振动加速度幅值-车速关系曲线

图18为支承横梁最大竖向位移与车辆行驶速度关系折线图，图19为支承横梁竖向振动加速度幅值与车辆行驶速度关系折线图。

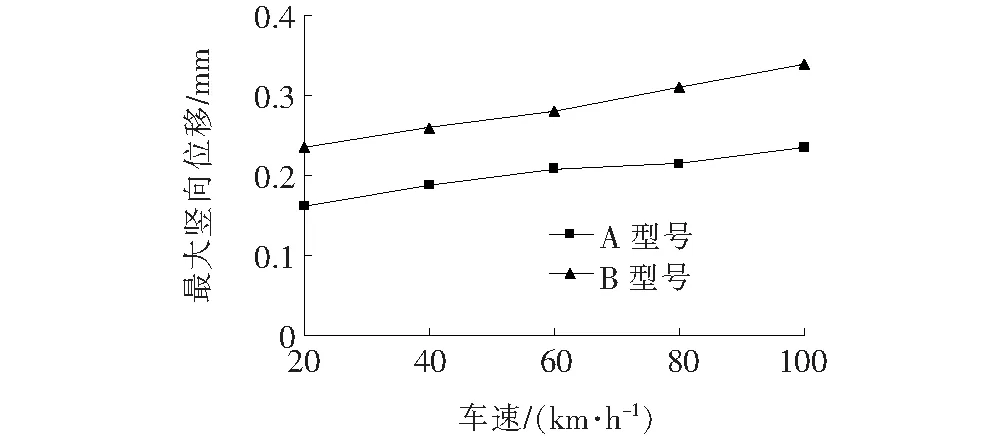
图18 支承横梁竖向最大位移-车速关系曲线

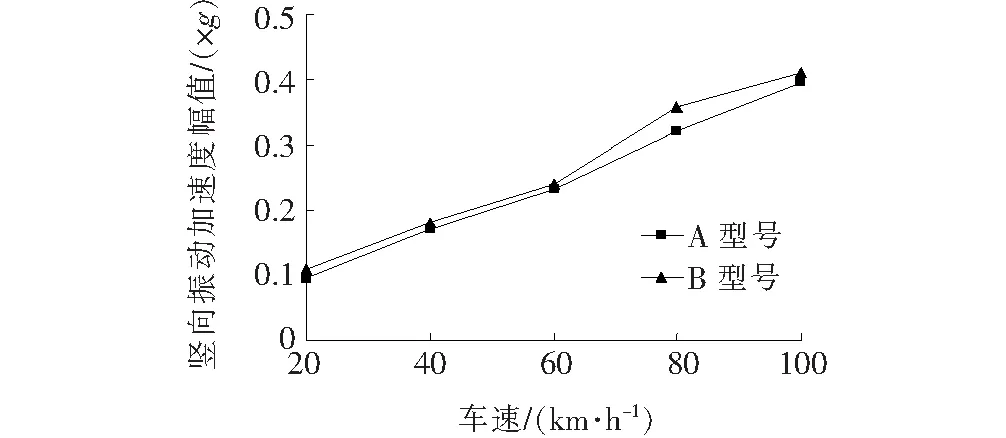
图19 支承横梁竖向振动加速度幅值-车速关系曲线

从图18、19可以看出：随着车速的增加，支承横梁所产生的最大竖向位移及竖向振动加速度幅值均增加；相同速度下，轮胎经过A型伸缩装置时支承横梁最大竖向位移及竖向振动加速度幅值均小于B型伸缩装置。

由以上计算结果可知：随着车速逐渐增加，伸缩装置所受到的冲击效应逐渐提升，各部件所产生的位移也随之增加。综合对比两型号伸缩装置齿板及支承横梁在动态车辆荷载作用下产生的最大竖向位移及竖向加速度幅值，可以认为车辆在通过A型伸缩装置时，行车平稳性更优，驾驶员颠簸感更小。

4 结论

(1)汽车荷载作用下多向大变位伸缩装置各部件强度及刚度均满足设计要求。汽车轮载全部作用于活动齿板顶面时(工况1)，伸缩装置各部件产生更高的等效应力和更大的变形。两种型号伸缩装置中，A型号伸缩装置具有相对更高的强度及刚度安全储备。

(2)多向大变位伸缩装置活动齿板与支承横梁采用螺栓连接，后期维修时，便于拆卸进行局部更换。螺栓作为连接件，疲劳破坏对其耐久性起主要影响作用，通过不同工况的计算可以看出，连接螺栓在汽车荷载作用下，具有相对较低的等效应力值，这有助于连接螺栓抵抗疲劳破坏，证明了活动齿板与支承横梁采用螺栓连接的可行性。在工程应用中，可根据道路交通量以及典型车辆吨位，适当增加螺栓数量以防止螺栓发生疲劳破坏。

(3)对两种型号伸缩装置在不同车速下的动力响应进行了有限元计算，计算结果表明：车辆通过多向大变位伸缩装置时，随着车速的增加，活动齿板最大竖向位移与竖向加速度逐渐增大；两种型号伸缩装置相比，相同车速下，A型号伸缩装置能够提供更好的行车平稳性，并且齿板竖向振动加速度更小，有助于降低伸缩装置的振动噪声。