城市轨道交通站间距计算模型

武倩楠，淡鹏瑞, ，李 杨，李昌宇

（1.南京铁道职业技术学院 运输管理学院，江苏 南京 210031；2.无锡地铁运营有限公司 客运服务部，江苏 无锡 214000；3.德克萨斯大学奥斯汀分校 建筑学院，德克萨斯 奥斯汀 78712)

0 引言

目前城市轨道交通在快速发展，其规划理论却并不完善，导致部分站点布设与客流需求不匹配，严重影响城市轨道交通功能的发挥。虽然有关规范给出了站间距的参考值，但具体到每个城市中，不同线路的长度、沿线客流均有不同，不能采取单一站间距标准，因此需对合理站间距进行研究。

国外对于站间距的研究很多是针对道路公交，Chien等[1]考虑乘客出行的可达性，建立起基于总成本最小的交通线路站间距优化模型；Ceder等[2]考虑了地形条件非均衡性对步行速度、公交服务吸引能力和公交车加速度的影响，对常规公交系统站间距的优化问题进行了研究。国内研究主要集中在2个方面，一是分析车站选址是否合理，其中李君等[3]从票价收益、土地开发收益、工程造价、运营费用等方面对增设车站是否合理进行定量分析；程国柱等[4]从客流量、乘客出行成本和运营成本方面，构建双层选址模型。二是对线路的合理站间距进行研究，其中左大杰等[5]从劳动力对于经济社会的影响出发，认为乘客出行时间最少应该是交通设施追求的目标，建立了最优站间距计算模型，李婷等[6]继续完善该方法，将乘客接驳范围划分为步行吸引范围、公交车—自行车吸引范围，并假设轨道交通线网发展到一定程度呈现“棋盘式”；赵淑芝等[7]计算出3种形态下的城市半径，构建基于城市规模的平均站间距模型。

目前研究中对站间距与乘客接驳时间的关系研究不够深入，忽略路网形态的影响，且没有体现接驳方式的差异。另外，随着城市扩张，不同区域的乘客平均出行距离差异较大，采用整个城市的平均出行距离计算整条线路的平均站间距也已经不再适应。基于乘客出行时间角度，细化乘客接驳范围，考虑客流分布情况和不同路网形态，建立城市轨道交通站间距计算模型，为城市轨道交通规划与设计提供借鉴。

1 乘客出行时间影响因素分析

1.1 乘客出行时间组成

选择城市轨道交通方式出行的乘客，其出行时间包括从出发地到起始车站的接驳时间t1，s；在城市轨道交通系统内部的时间t2，s；从终点车站到目的地的接驳时间t3，s。其中，在城市轨道交通系统内部的时间包括进站检票时间t4，s；候车时间t5，s；乘客在车时间t6，s；出站检票时间t7，s。乘客出行时间T可表示为

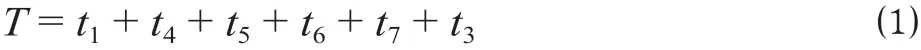
其中，进站检票时间t4、出站检票时间t7、候车时间t5，主要受到车站设施布局和列车发车间隔的影响，只有接驳时间t1和t3(假设从出发地到起始车站、从终点车站到目的地的接驳时间相等)、乘客在车时间t6会受到站间距的影响。由于站间距设置需要考虑客流需求，在对接驳时间t1和t3分析中需加入客流密度函数，体现每个车站周围的客流情况对车站设置的影响；乘客在车时间t6需要结合站间OD预测数据，由于在规划阶段，城市轨道交通线路沿线土地利用情况并不一定非常明确，预测OD数据可能会产生较大误差，故将该线路所经区域的乘客平均出行距离设为变量，乘客在车时间t6与站间距之间的关系参考已有研究[6]，其计算公式为

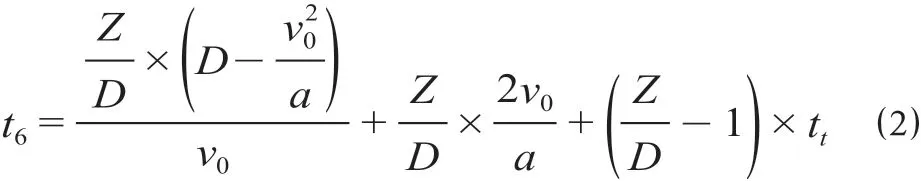
式中：Z为乘客平均出行距离，m；D为平均站间距，m；v0为列车最高运行速度，m/s；a为列车加速度(设加速度和减速度相等)，m/s2；tt为列车停站时间，s。

1.2 乘客接驳时间分析

城市轨道交通车站是客流集散的场所，乘客从出发地到车站(或从车站到目的地)需要通过某种接驳方式，如步行、自行车、公交车等。站间距越小，车站数量越多，乘客到达车站的接驳时间会越短；相反地，站间距越大，车站数量越少，乘客到达车站的接驳时间会越长。

由于城市轨道交通的到站客流以步行、自行车、公交车为主，自行车和公交车的速度相差不大，可将车站的客流吸引范围划分为步行吸引范围、自行车—公交车吸引范围。单位土地面积产生的客流量称为客流密度，可以表达成到站距离r的函数p(r)，人/m2；设城市轨道交通线路总长度为L，m；车站步行吸引范围半径为R1，m；步行速度为v1，m/s；客流密度为p1(r)，人/m2；自行车—公交车吸引范围半径为R2，m；自行车/公交车速度为v2，m/s；客流密度为p2(r)，人/m2。第i个车站吸引范围内产生的总客流量Pi，可利用极坐标进行二重积分，计算公式为

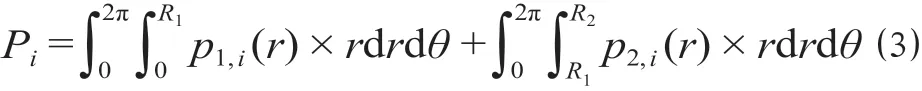
式中：p1,i(r)为第i个车站的步行吸引范围客流密度，人/m2；p2,i(r)为第i个车站的自行车—公交车吸引范围客流密度，人/m2。

考虑目前城市路网形态主要有方格路网和放射路网2种，需分以下2种情况计算平均接驳时间。在放射路网形态下，接驳距离近似为出发地到起始车站的空间直线距离，其平均接驳时间为

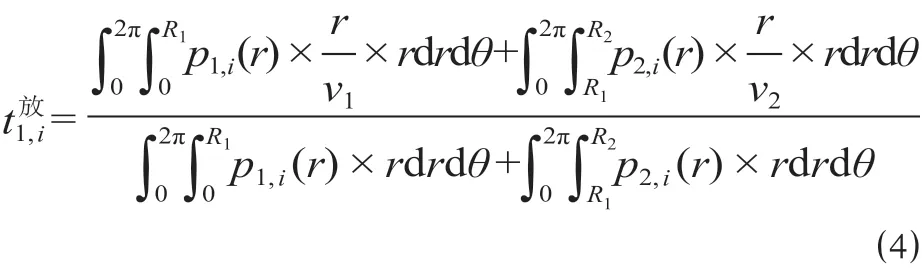
在方格路网形态下，接驳距离近似为矩形的长边和短边之和，平均接驳时间为

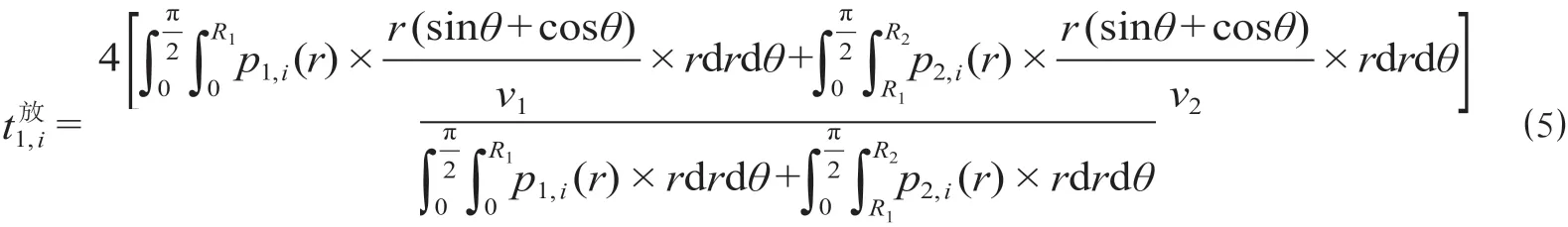
2 站间距计算模型

将乘客接驳时间及在车时间代入到乘客出行总时间T，可以得到关于乘客出行总时间T与站间距D的函数T(D)，基于乘客出行时间最短，需对该式进行求导，即T′(D) = 0，求得站间距计算模型。

2.1 乘客接驳时间模型

乘客接驳时间上述分析是在一般情况下的结果，为方便计算做出以下假设：①整条线路的各个车站步行吸引范围半径R1都相等，自行车—公交车吸引范围半径R2都相等；②步行吸引范围内的乘客均匀分布，客流密度为p1；自行车—公交车吸引范围内的乘客均匀分布，客流密度为p2。

利用极坐标二重积分计算公式，可以计算出乘客平均接驳时间。

（1）放射路网情况下，以步行吸引范围为例，根据公式(4)，可以计算得到步行吸引范围的乘客平均接驳时间为

同理可得，步行吸引范围和自行车—公交车吸引范围内的乘客平均接驳时间为

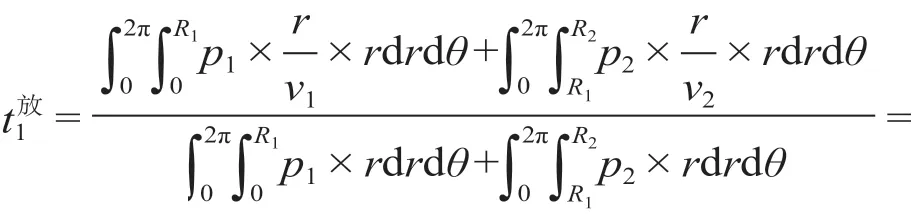
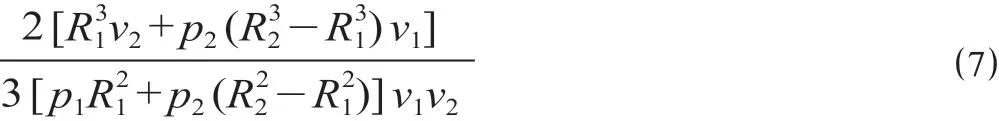
（2）方格路网情况下，以步行吸引范围为例，根据公式(5)，可以计算得到步行吸引范围的乘客平均接驳时间为

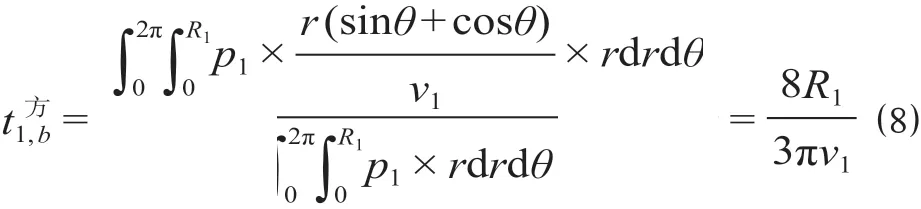
同理可得，步行吸引范围和自行车—公交车吸引范围内的乘客平均接驳时间为

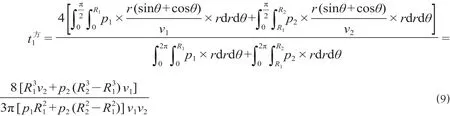
可以看出，方格路网情况下的乘客平均接驳时间和放射路网情况下差别较大。国内大部分城市的住宅小区、商业区、学校等都为矩形，路网以方格网为主，所以该种情况下计算出来的平均接驳时间较为符合现实情况。

2.2 站间距计算模型

根据已有研究，城市轨道交通的步行接驳范围半径一般为0.4 ～ 0.8 km左右，自行车—公交车接驳范围半径一般为0.8 ～ 3 km左右[8-9]。在市区范围，站间距较小，到站乘客以步行为主，相邻两站间自行车—公交车、步行吸引范围均会有重叠；在城市郊区范围，站间距较大，相邻两站间步行吸引范围无重叠，自行车—公交车吸引范围有重叠。假设重叠部分被平均分配到相邻两站，则在市区R1可以用取代，此时车站吸引范围内的乘客平均接驳时间只需考虑步行乘客；在郊区R2可以用取代，此时车站吸引范围内的乘客平均接驳时间只需考虑自行车—公交车乘客。

（1）放射路网情况下，需按照市区和郊区2种情况进行考虑。

将公式(2)、公式(10)代入公式(1)，得到在市区放射路网情况下的乘客出行总时间T与站间距D间的函数公式

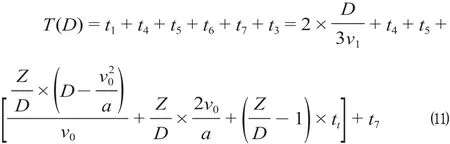
令T′(D) = 0，得到乘客出行总时间T最短时的站间距D计算公式

同理可得，当在郊区放射路网情况下，乘客出行总时间T最短时的站间距D计算公式

（2）方格路网情况下，需按照市区和郊区2种情况进行考虑。

将公式(2)、公式(14)代入公式(1)，得到在市区方格路网情况下的乘客出行总时间T与站间距D间的函数公式

令T′(D) = 0，得到乘客出行总时间T最短时的站间距D计算公式

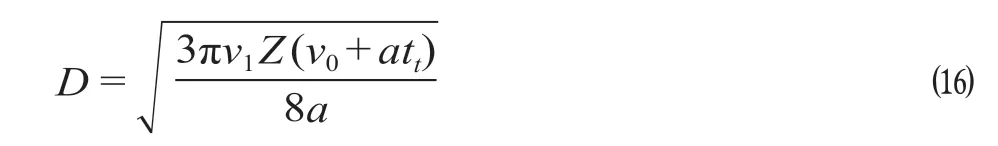
同理可得，当在郊区方格路网情况下，乘客出行总时间T最短时的站间距D计算公式

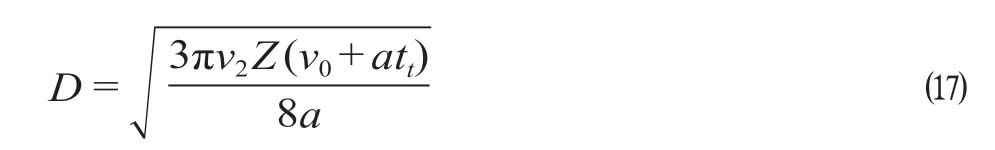
综上所述，站间距计算需分4种情况，分别是市区—放射路网、郊区—放射路网、市区—方格路网、郊区—方格路网。

3 算例分析

从站间距模型计算公式可以看出，站间距D与乘客平均接驳速度v1和v2、乘坐轨道交通的平均出行距离Z、列车最高运行速度v0、列车停站时间tt及列车加速度a有关。利用控制变量法，可以研究各个参数的变化对于站间距的影响情况。随着城市扩张，不同区域的乘客平均出行距离差异较大，会对计算整条线路的站间距影响较大，因此以乘坐轨道交通的平均出行距离这一变量为例进行分析说明。

3.1 参数取值

对乘客平均接驳速度v1和v2、列车最高运行速度v0、列车停站时间tt、列车加速度a及乘坐轨道交通的平均出行距离Z参数做出如下说明。

（1）乘客平均接驳速度v1和v2。根据已有研究，一般步行速度为4 ～ 5 km/h[10]，自行车速度为15 ～ 20 km/h[11]，公交车旅行速度为15 ～ 20 km/h[12]，考虑到乘客年龄跨度大、接驳路网路况复杂，因此乘客步行平均速度取4 km/h，自行车/公交车平均速度取15 km/h。

（2）列车最高运行速度v0。根据《地铁设计规范》(GB 50157—2013)，列车最高运行速度有80 km/h，100 km/h，其中80 km/h的线路数量较多，因此列车最高运行速度取80 km/h。

（3）列车停站时间tt。根据已有研究[13]，列车在不同站、不同时段停站时间都不同，为方便计算取平均值30 s。

（4）列车加速度a。根据《地铁车辆通用技术条件》(GB/T 7928—2003)，列车从0加速到40 km/h，不低于0.83 m/s2，因此列车加速度取1 m/s2。

（5）乘坐轨道交通的平均出行距离Z。从已有研究可以得出结论，城市不同区域的乘客平均出行距离是不同的。一般居住在市区的乘客平均出行距离较短，而居住在城市郊区的乘客平均出行距离较长。根据文献[14]中对全国各城市轨道交通线路平均运距调查可知，全国24个城市108条线路平均运距范围为2.95 ～ 24.32 km，其中平均运距在6 ～ 18 km范围内的线路共计86条，占总线路条数的80%，故乘坐轨道交通的平均出行距离Z，取市区为6 ～ 12 km，郊区为12 ～ 18 km。

3.2 计算结果分析

根据上述参数的设定，在乘客平均接驳速度、列车最高运行速度、列车停站时间、列车加速度这4个参数固定的情况下，可以得到站间距随轨道交通平均出行距离的变化情况。通过公式(12)、公式(13)、公式(16)、公式(17)计算得到市区—放射路网、郊区—放射路网、市区—方格路网、郊区—方格路网4种情况下的站间距变化情况，站间距随轨道交通平均出行距离变化趋势图如图1所示。4种情况下对应的站间距上下限如表1所示。

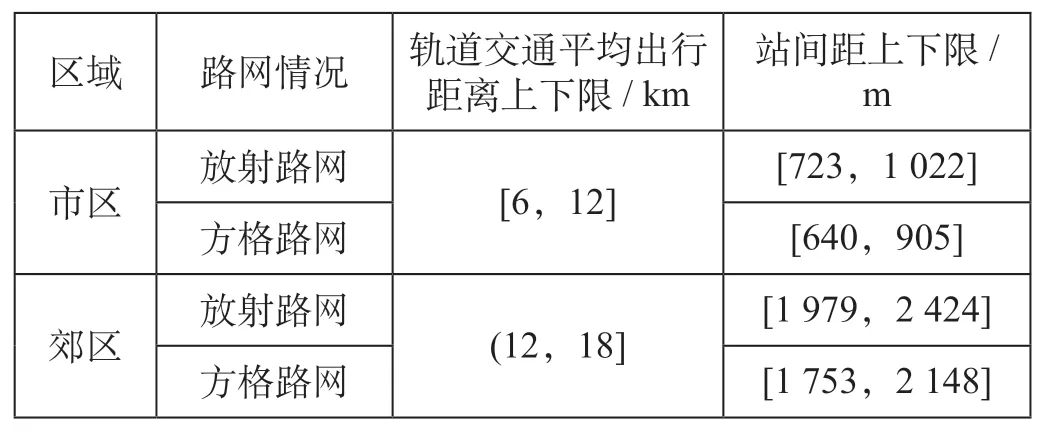
表1 4种情况下对应的站间距上下限Tab.1 Upper and lower limits of station spacing in four cases

由图1和表1可以看出，最优平均站间距随轨道交通平均出行距离的增加而增加，且不同路网条件下差异较大。在放射路网情况下，市区的站间距在723 ～ 1 022 m范围内；在方格路网情况下，市区的站间距在640 ～ 905 m范围内。市区2种路网情况下的站间距与《地铁设计规范》中给出的“市区宜在1 km左右”的指导值相比略偏小。在放射路网情况下，郊区的站间距在1 979 ～ 2 424 m范围内，与《地铁设计规范》中给出的“郊区宜在2 km左右”的指导值相比偏大；在方格路网情况下，郊区的站间距在1 753 ～ 2 184 m范围内，与《地铁设计规范》中给出的“郊区宜在2 km左右”的指导值相比差距不大。

图1 站间距随轨道交通平均出行距离变化趋势图Fig.1 Variation trend of station spacing with average travel distance by rail transit

目前很多城市轨道交通线路连接市区和郊区，长度较长，所以计算站间距时，不能采取单一的平均出行距离来计算整条线路的平均站间距，而是应该分区域调查乘客平均出行距离，分别计算各个区域的平均站间距。

4 研究结论

基于乘客出行时间最短，建立了市区—放射路网、郊区—放射路网、市区—方格路网、郊区—方格路网4种情况下的站间距计算模型，在给定路网形态和平均出行距离时可以计算得到相应的站间距，主要结论如下。

（1）在对乘客平均接驳时间进行细化时发现乘客接驳距离与路网形态密切相关，且方格路网和放射路网情况下的差异较大。

（2）在设定的市区6 ～ 12 km、郊区12 ～ 18 km的平均出行距离范围下，市区的站间距范围在放射路网和方格路网下分别为723 ～ 1 022 m，640 ～ 905 m，郊区的站间距范围在放射路网和方格路网下分别为1 979 ～ 2 424 m，1 753 ～ 2 184 m。

（3）相同的平均出行距离情况下，不同路网形态、城市不同区域的站间距差别较大，因此对于连接郊区和市区的长度较长的线路，应该分区域调查乘客平均出行距离，分别计算各个区域的平均站间距。

在模型构建过程中，虽然客流函数被引入乘客接驳时间中，但由于其函数形式缺乏较权威的参考，没有体现在最终的模型中，接下来需要对此进一步研究和优化。