基于任务均衡的乘务排班计划优化编制方法研究

陈霁岩，潘寒川，刘志钢，吴 强，赵 磊

（1.上海工程技术大学 城市轨道交通学院，上海 201600；2.上海地铁第二运营有限公司，上海 200063；3.上海地铁第二运营有限公司 质量安全部，上海 200063）

0 引言

乘务计划是城市轨道交通运营中的重要环节，主要解决轨道交通乘务员的值乘问题。国内多数城市轨道交通的乘务计划由各线路乘务部门编制完成，消耗时间长，变更难度大。乘务计划分为乘务排班计划与乘务轮转计划，其中乘务排班计划根据给定的列车运行图，将运行线根据线路条件与乘务制度进行分割与重组，从而得到可行的任务号集合；乘务轮转计划则是在当期各个运行图的乘务排班计划编制完毕后，根据列车运行图属性(工作日、节假日、延长图等)按照一定的规则使得乘务员轮流执行任务。乘务排班计划作为乘务计划的第一步，其编制质量对整个乘务计划编制结果有直接的影响。

近年来，乘务排班计划编制优化在国内外引起学者广泛的研究，Michael等[1]应用图论解决城市轨道交通车底运用和乘务计划中的每个子问题，不同于以往完成编制运行图后再编制乘务计划，而是同时进行运行图与乘务计划编制，后计算实例证明比现实际使用更低。根据香港轻轨乘务排班计划的特点，Chu等[2]将乘务排班计划分为2个阶段进行研究，依次采用最短路算法、对称匹配及改进的遗传算法进行求解。Elizondo等[3]在对城市轨道交通乘务计划建模时，采用人工智能领域的方法来表示状态空间，分别使用基于网络图的贪心搜索和禁忌搜索算法来解决问题，最后通过数据进行验证。针对城市轨道交通的特点，李献忠等[4-5]提出3种乘务排班优化模型，分别为基于广义费用最小成本、时间成本最小和总时间消耗最小，并采用禁忌搜索算法、模拟进化算法和最小费用最大流算法对模型进行求解。潘寒川等[6]在考虑乘务员用餐的约束条件下，提出DHM和VGM 2种编制方法，探讨 2 种方法在多个“就餐点”及“网络线路乘务员共享”方法下的适用性和可行性。针对目前不同地铁线路具有不同的高峰系数，潘寒川等[7]提出CRM 和PIM 乘务计划编制方法，可针对线路情况选择不同编制方法，提高精细化管理。

目前针对乘务排班计划编制问题的模型及算法研究较多，但在编制中综合考虑城市轨道交通乘务制度的相关研究较少[8-9]。随着各个城市地铁兴建与发展，乘务制度与乘务规则开始出现差异化。目前国内部分线路开始采用计件制薪资方案，即综合计算开行里程与工时计薪。通常乘务班组中每个乘务员的开行公里数与值乘时长是不均衡的，除了导致乘务员收入无法得到均衡，还会使得部分乘务员值乘时间过长从而存在安全隐患。因此，在既有研究基础上提出以任务均衡为目标的乘务排班计划编制模型，构建经典集合分割主问题模型及基于任务均衡与乘务特色约束子问题模型。利用计算机编程语言实现主规划部分求解，同时设计基于影子价格选择的标号法用于求解子规划部分，并以上海市轨道交通某条线路为例，验证模型与算法的有效性和效率性。该方法拟寻求在实际运营中科学合理地控制成本，提高运输效率，促进企业长期可持续发展，加强企业精细化管理，同时也为乘务排班计划问题的研究提供理论依据。

1 基于任务均衡的乘务排班计划优化编制方法研究

1.1 乘务排班计划编制影响因素分析

乘务排班计划编制问题本质上是一个指派问题，是将乘务员与列车进行绑定的过程，即在规定的乘务员数量下，指派相应的乘务员执行部分列车开行任务，从而保证每个运营时间段的每列列车均有乘务员值乘。城市轨道交通每条线路由停车场、车站与轨道组成。停车场是列车出库、回库、维修养护及乘务员办理出勤、退勤的地点；车站根据功能可划分为：轮乘站、交接站、就餐站。

（1）轮乘站设置对于乘务排班计划编制影响。根据《国务院关于职工工作时间的规定》：“因工作性质或者生产特点的限制，不能实行每日工作8 h、每周工作40 h标准工时制度，按照国家有关规定，可以实行其他工作和休息办法。”由于乘务员工作性质的特殊性，通常规定乘务员在连续驾驶1 h左右需进行休息，从而保证行车安全，避免疲劳驾驶。各个线路管理部通常根据线路长度、车站位置及设施设备条件设定数个轮乘站，供乘务员在连续驾驶一定时长后下车休息。通常以轮乘间隔来规定休息时长，若乘务员A需要休息n个轮乘间隔，则当乘务员A在轮乘站下车休息后，在驶过n辆列车后(包含乘务员下车时所驾驶列车)，当第n+ 1辆列车进站后替换该列车乘务员B继续驾驶，乘务员B开始轮乘休息。乘务轮乘过程如图1所示(该站轮乘间隔为2)。

（2）交接站设置对于乘务排班计划编制影响。由于目前城市轨道交通线路长度不断延长，仅靠停车场提供出退勤管理已无法满足线路乘务排班计划编制需求，通常由线路管理部综合车站设施设备条件、乘务员住址等设立交接站从而满足乘务员出退勤需求。交接站设置个数的增加，会使得乘务任务生成更加灵活，但同时会导致排列组合的可能性增加，使得求解难度上升。

（3）就餐站设置对于乘务排班计划编制影响。乘务员的工作班制通常为四班三运转，即日—夜—早—休，其中日班工作时长会覆盖午餐时间，为满足乘务员午餐需求，需设定具备条件站点为就餐站，保证日班每位乘务员可在11 : 00—13 : 00完成就餐。就餐站的数量根据线路长度决定，每条线路通常设置1至2个就餐站于线路中间位置，供乘务员就餐、休息。

对于乘务排班计划编制而言，由于在非功能性车站通常不会进行乘务员的变换，因而非功能性车站不会影响乘务排班计划编制。为此，在后续模型构建及算法设计过程中，将乘务数据进行筛选，仅考虑功能站的列车到发。

1.2 基于任务均衡的乘务计划优化编制模型构建

乘务排班计划编制问题，是一个典型的NPhard问题，随着线路复杂程度的提升，变量的数目会随之呈爆炸式增长。在乘务排班计划编制问题中，唯一需要分配的资源是乘务员，编制过程为将列车运行线按轮乘站、交接站进行分割后，按一定的规则进行重组，主要输入数据如下。①一段时间内的列车运行图数据：包括列车车底号、列车在各个站点的到发时间、交路信息号；②线路基本条件：包括全线路站点、轮乘站、就餐站及其轮乘间隔、交接站、停车场位置；③对生成任务号的硬约束：乘务员值乘区段全覆盖、值乘区段邻接、乘务员单次值乘时间上下限；④对生成任务号的软约束：时间均衡度、里程均衡度、乘务员偏好。输出数据为任务号表，包含任务号个数与各个任务号的开行路径，每个任务即对应一个乘务员的每日任务，输出结果必须满足所有硬约束、符合线路条件，同时尽量将成本降至最低并保证一定的均衡度，直至乘务排班计划编制完毕。

1.2.1 主问题模型构建

在以往的城轨乘务排班计划编制研究中，通常采用集合覆盖模型与集合分割模型建立乘务问题模型[10]。集合覆盖模型允许编制的排班计划中存在随乘情况，即一位乘务员在A站下车，但无法在A站接到后续规定时间内的车次，需搭乘列车随乘到B站接车。随乘情况的增加降低了乘务排班计划整体的工时有效率，增加了运营开支，采用集合分割模型建立主问题模型，具体如下。

式中：z为总成本，是最后生成并选入乘务排班计划的所有乘务任务成本之和；cj为第j个乘务任务的成本；aij表示生成的第j个乘务任务是否包含乘务片段i，包含则aij= 1，不包含则aij= 0；xj表示第j个乘务任务是否采用，采用则xj= 1，不采则xj= 0；U为乘务片段集合；R为乘务任务集合，每个乘务任务包含1个或多个乘务片段。

为对此问题进行求解并获取其对偶变量，需先将主问题进行线性松弛得到一个线性规划问题，在迭代完成后，对主问题采用分支定价法进行剪枝从而得到0-1整数解，线性松弛后的模型如下。

1.2.2 子问题模型构建

在主问题中，仅考虑了乘务任务对于乘务片段的全覆盖，对于轮乘、单次值乘时间、总值乘时间等约束则在子规划中考虑。子规划模型建立如下。

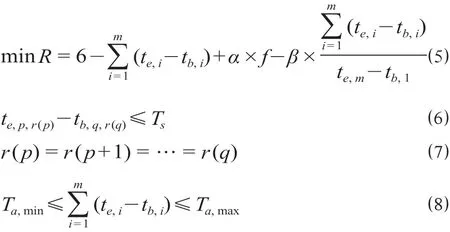
式中：R为所生成的新乘务任务的总费用；te,i为第i个乘务片段的到达时间，s；tb,i为第i个乘务片段的发出时间，s；α为超时未休惩罚权重系数；f为连续驾驶时长超1.2 h未休息次数；β为工时有效率权重系数；r(p)为所生成乘务任务中第p个乘务片段车底号；te,p,r(p)为所生成乘务任务中第p个乘务片段的到达时间，s；tb,q,r(q)为所生成乘务任务中第p个乘务片段的发出时间，s；Ts为单次连续值乘最大时长，s；Ta,min，Ta,max为当日最小、最大值乘时间，s。

由于所选的上海地铁线路乘务数据初始数量为18 000条，在对数据经过清洗和筛选重组后，乘务数据量减少为1 500条。而在以往的研究中，通常数据量在500左右，这与上海地铁的线路长度、开行间隔、客流数与线路较为复杂存在一定的关系。由于主规划和子规划每迭代一次就需要对子问题进行一次求解，若采用以往研究中的方法求解子问题可能会导致求解速度过慢。以求解主问题所得的对偶变量最大值所对应的节点为起始点进行搜索，并选取生成后数个子问题目标函数最小的乘务任务，添加入主问题，从而加速求解并保证解的质量。

当算法迭代至不存在检验数小于0时，重设主问题目标函数，以求得值乘时长与里程均衡。

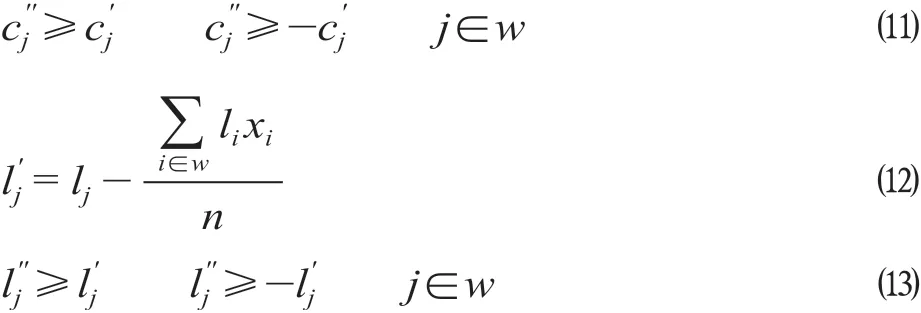
式中：γ为时长均衡权重系数；δ为里程均衡权重系数；n为迭代完毕后主问题中乘务任务的总数量；w为迭代完毕后主问题中乘务任务集合；cj为第j个乘务任务值乘时间费用；lj为第j个乘务任务值乘里程，km。

1.3 基于任务均衡的乘务排班计划优化编制模型求解

1.3.1 成本函数

主问题在进行线性松弛之后，得到的问题为一个线性规划问题。对于一个线性规划问题，通常的解决办法是利用单纯形法进行求解。一个标准的线性规划问题如下。

式中：cT为线性规划问题的成本系数向量；x为变量向量；A为变量系数矩阵；b为约束右端常数项向量。

公式(14)可通过公式(15)进行变换代入得到公式(16)，其中下标B表示基变量，下标N表示非基变量。

观察公式(16)右端容易得到，左边加项对于一个既定的问题，是一个常数。右边加项若∃n∈N使得则可以适当增加xN的值，使得目标值更优；若则此时令所有非基变量取0，可获得最优解。因此，在单纯形法中称为检验数。

1.3.2 迭代方法

列生成思想求解过程则是利用上述推导，首先在主问题中构造一个初始可行解，随后在子问题中检索是否存在乘务任务xj使得检验数小于0。若存在，则说明将此任务加入到主问题可以使得主问题进一步优化。当子问题中所有乘务任务的检验数均大于等于0时结束迭代，并对主问题进行剪枝后求解得出编制结果。列生成思想求解过程如图2所示。

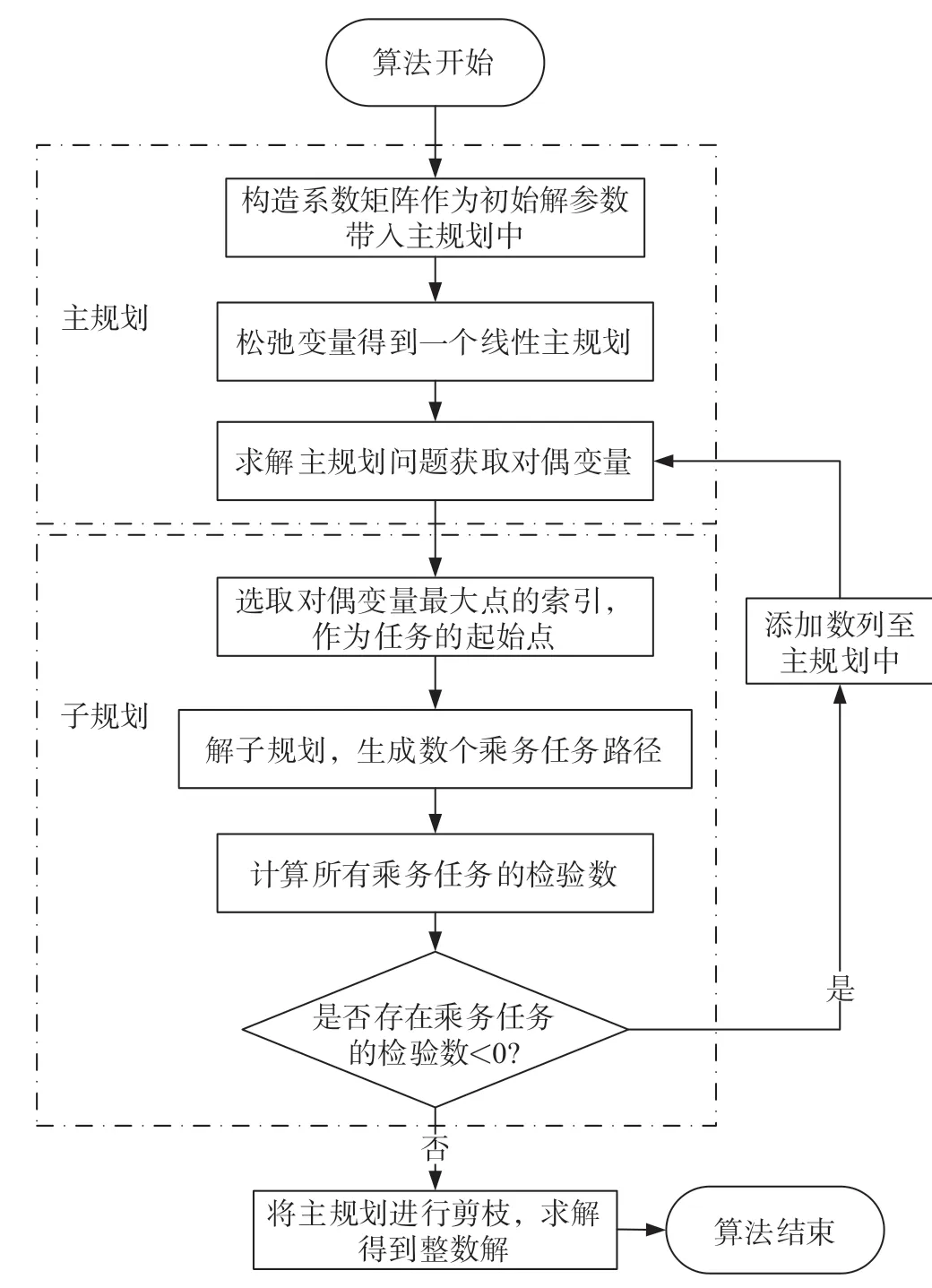
图2 列生成思想求解过程Fig.2 Solving process in column generation

2 实例分析

以上海市某条轨道交通线路为例，对所建立的模型算法进行求解验证。该线由西至东总长38.83 km，共有31个车站、3个轮乘站与2个停车场，现有乘务排班计划主要依靠人工经验进行编制，模型构建及算法设计通过计算机编程语言实现。

2.1 数据处理

乘务排班计划编制的数据为信号系统所记录的数据，内容为：车次号、车站名、到点、发点、交路号等。此时的数据规模较大，若直接对此进行计划编制，会导致求解速度过慢或内存溢出。而在乘务排班计划编制中，非功能站(轮乘站、交接站、出退勤站)乘务员通常不会有更换车底值乘的动作，因而对数据进行清洗重组处理。数据清洗重组过程如图3所示。

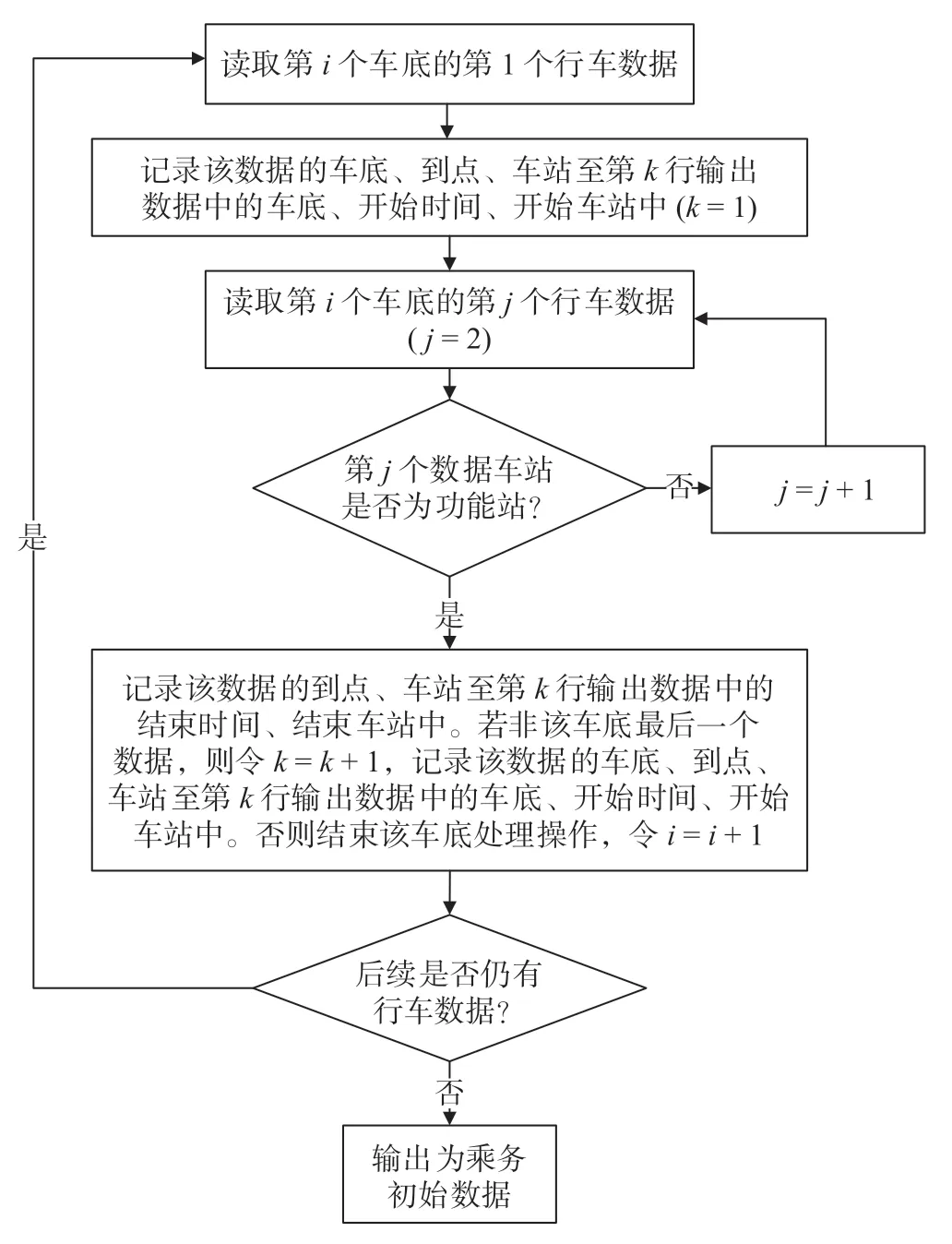
图3 数据清洗重组过程Fig.3 Data cleaning and reorganizing process

乘务数据清洗重组思路基本适用于大部分的地铁线路乘务排班计划，处理后的结果可直接由模型算法程序进行读取求解计算。

2.2 导入求解

所建模型中需输入参数共有4个：α为值乘超1.2 h未休息次数惩罚权重系数；β为工时有效率权重系数；γ为值乘时间费用均衡度权重系数；δ为值乘里程均衡系数。在计算值乘时间费用成本时，取α= 0.3，β= 1。在求值乘时间费用与值乘里程均衡时，取γ= 2，δ以数值间隔为0.1在0.5 ～ 1.5间取值进行多次计算，不同δ权重系数下的值乘时间费用均衡度如图4所示，不同δ权重系数下的值乘里程均衡度如图5所示，不同δ权重系数下工时有效率如图6所示。

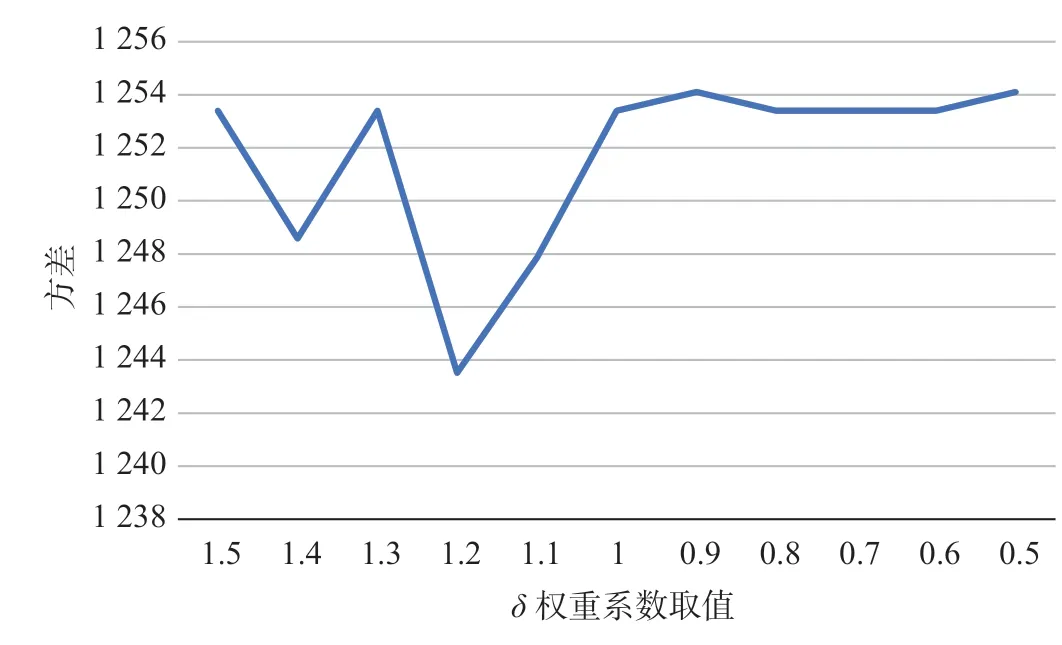
图5 不同δ权重系数下的值乘里程均衡度Fig.5 Rostering mileage balance at different weight coefficients δ

观察图4至图6可知，当δ取1.2时，所输出的乘务排班计划具有更优的任务均衡度与工时有效率。乘务任务输出如表1所示，其中以(1301) -(22 911，24 005) - (JYR3，JSJR2)为例进行说明，1301为车次号，为乘务员登乘重要凭证之一；(22 911，24 005)为该乘务作业段的开始时间与结束时间，从当日0点开始以秒计算，s； (JYR3，JSJR2)为该乘务作业段的开始地点与结束地点；“=”符号连接了相邻的2个乘务片段。

表1 乘务任务输出Tab.1 Crew taskoutput

图4 不同δ权重系数下的值乘时间均衡度Fig.4 Rostering time balance at different weight coefficients δ

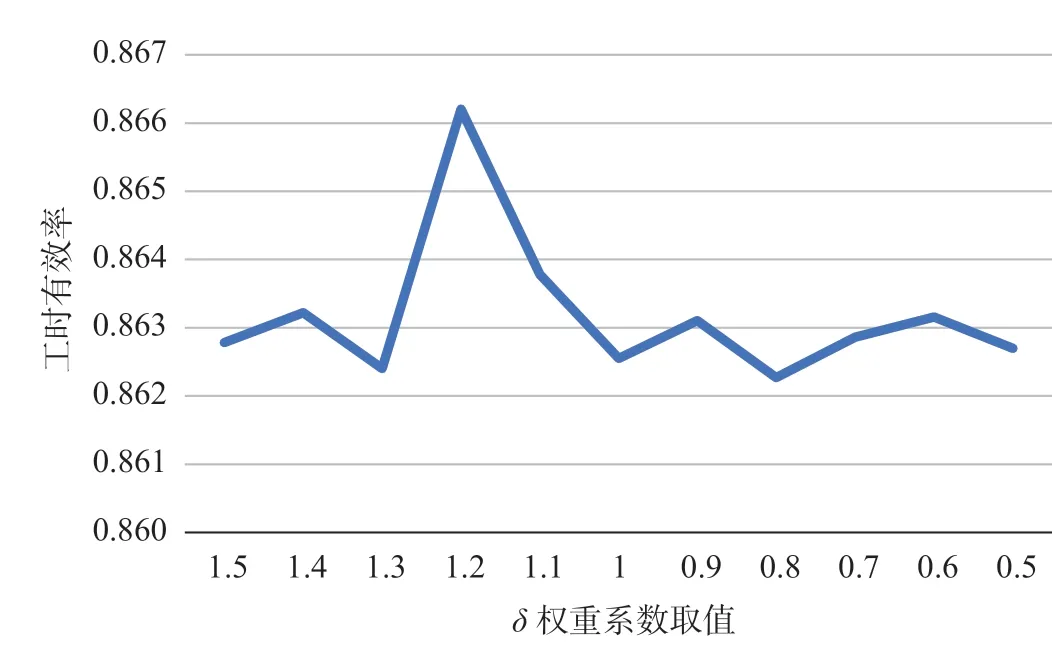
图6 不同δ权重系数下工时有效率Fig.6 Man-hour efficiency at different weight coefficients δ

δ取1.2时，乘务排班计划值乘时长与上班时长如图7所示，乘务排班计划值乘里程如图8所示，乘务排班计划工时有效率如图9所示。

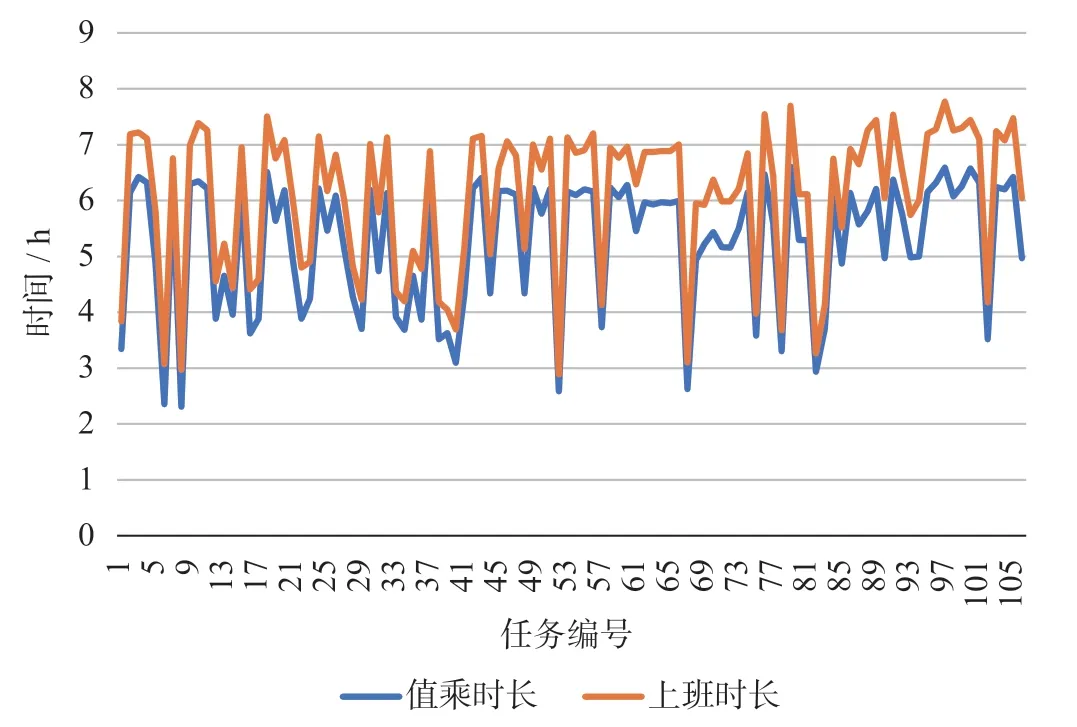
图7 乘务排班计划值乘时长与上班时长Fig.7 Rostering time and work time of crew scheduling

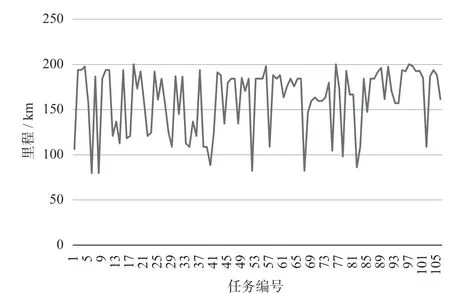
图8 乘务排班计划值乘里程Fig.8 Rostering mileage of crew scheduling

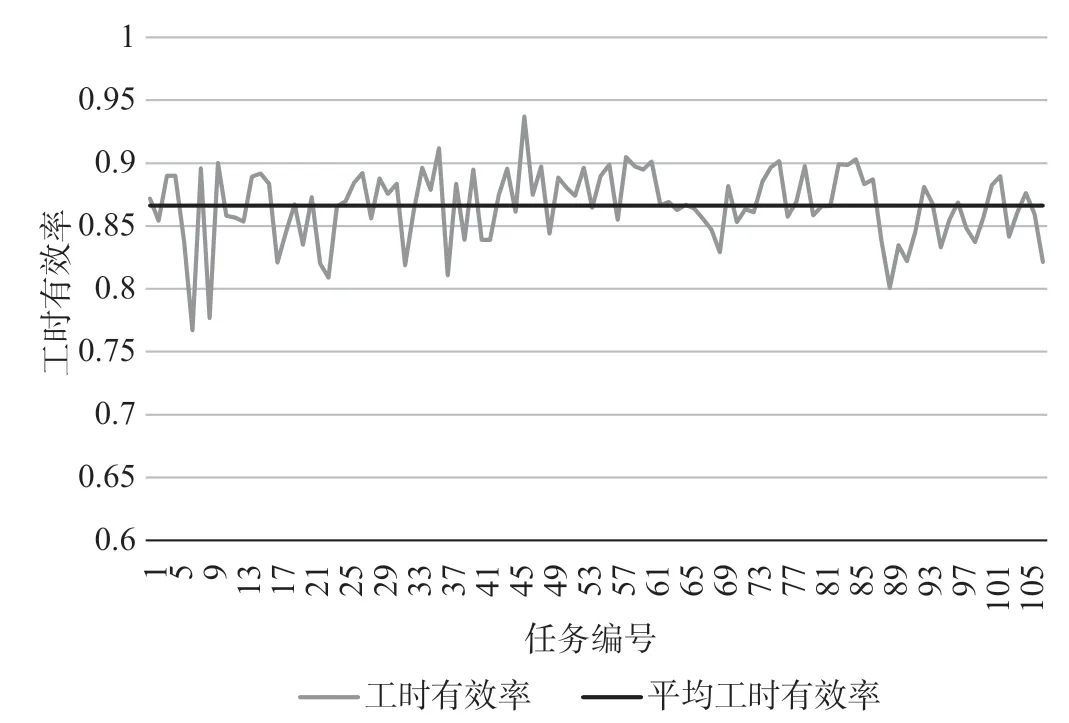
图9 乘务排班计划工时有效率Fig.9 Man-hour efficiency of crew scheduling

可见，基于任务均衡的乘务排班计划优化编制方法所计算求解的乘务任务具有较优的任务均衡和较高的工时有效率，平均工时有效率达到了86.6%。

3 结束语

基于任务均衡的乘务排班计划优化编制方法充分考虑目前城市轨道交通乘务员计件制薪资体系，以所生成的乘务排班计划成本最小为目标，构建集合分割主规划模型与乘务任务生成子规划模型，并设计基于影子价格选择的标号法进行求解完成迭代。案例分析中的求解结果验证了模型与算法的有效性和效率性，并且在上海地铁线路较大规模的乘务数据下仍有较好的求解速度，可适应未来城市轨道交通路网的进一步发展。方法中初始解所选取的系数矩阵为一个单位矩阵，优点是生成方法较为简便，缺点是一定程度上会影响求解的速度与结果，未来可针对如何快速构造一个较好的初始解进行深入研究。