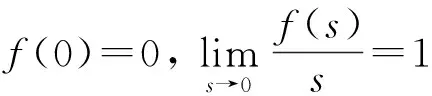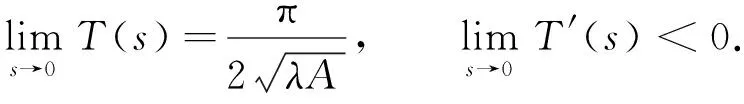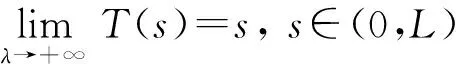带有特殊非线性项的Dirichlet问题正解的确切个数
2021-09-22姚燕燕高红亮
姚燕燕, 徐 晶, 高红亮
(兰州交通大学 数理学院, 兰州 730070)
1 引言与主要结果
考虑当非线性项为f(u)=u(eu-1)和f(u)=eu-1两种形式时, 一维Minkowski空间给定平均曲率方程Dirichlet问题
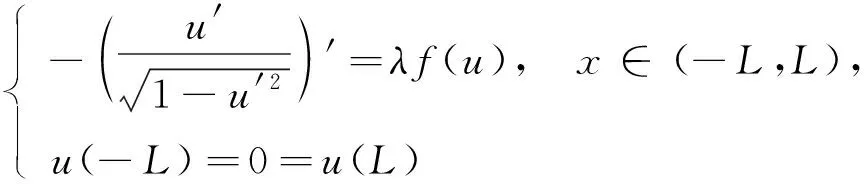
(1)
正解的确切个数及分歧图, 其中参数λ,L>0.
平均曲率问题是偏微分方程中的一个重要问题.设Ω⊂N为一个区域,k≠0是常数.考虑方程
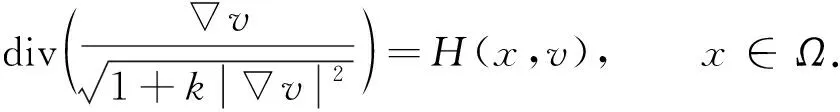
(2)
当k=1时, 方程(2)称为Euclidean空间中的给定曲率方程; 当k=-1时, 方程(2)称为Minkowski空间中的给定曲率方程.问题(1)是Minkowski曲率方程Dirichlet问题
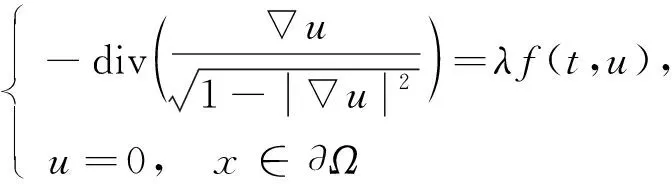
(3)
的一维情形.研究表明, 这些问题在微分几何和狭义相对论中具有重要作用[1-5].
近年来, 关于一维或高维Minkowski空间给定平均曲率方程Dirichlet问题的研究受到广泛关注, 如文献[6-14]用非线性分析的方法获得了问题(1)或(3)正解的存在性和多解性, 其中: Bereanu等[6]用Larea-Schauder度理论研究了非线性边值问题
(φ(u′))′=f(t,u,u′),l(u,u′)=0
解的存在性和多解性, 式中l(u,u′)=0表示在[0,T]上Dirichlet、 周期或者Neumann边界条件,φ: (-a,a)→是增同胚且φ(0)=0; Coelho等[7]用变分方法和拓扑度理论研究了一维Minkowski曲率方程Dirichlet问题(1)正解的存在性和多解性, 其中λ>0为参数; Bereanu等[8-9]利用临界点理论、 上下解方法和Larea-Schauder度理论讨论了Minkowski空间中Dirichlet问题(3)在球域上径向正解的存在性和多解性; Ma等[10]用分歧理论研究了球域上问题(3)正解的全局结构; Dai等[11]用分歧理论分别讨论了非线性项在零点渐近线性、 次线性和超线性情形下球域上问题(3)径向变号解的全局结构.
上述文献对平均曲率问题正解的存在性研究较多, 而对其正解的确切个数研究较少. Zhang等[12]用时间映像原理研究了问题
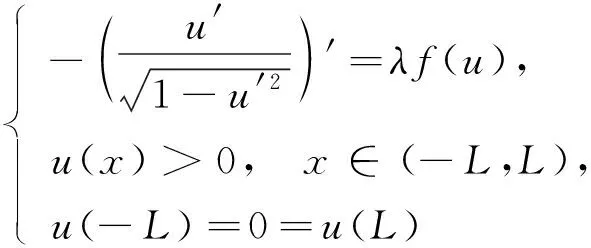
(4)
正解的确切个数及分歧图, 其中参数λ>0,L>0, 得到了如下结果.
定理1[12]假设f满足如下条件:
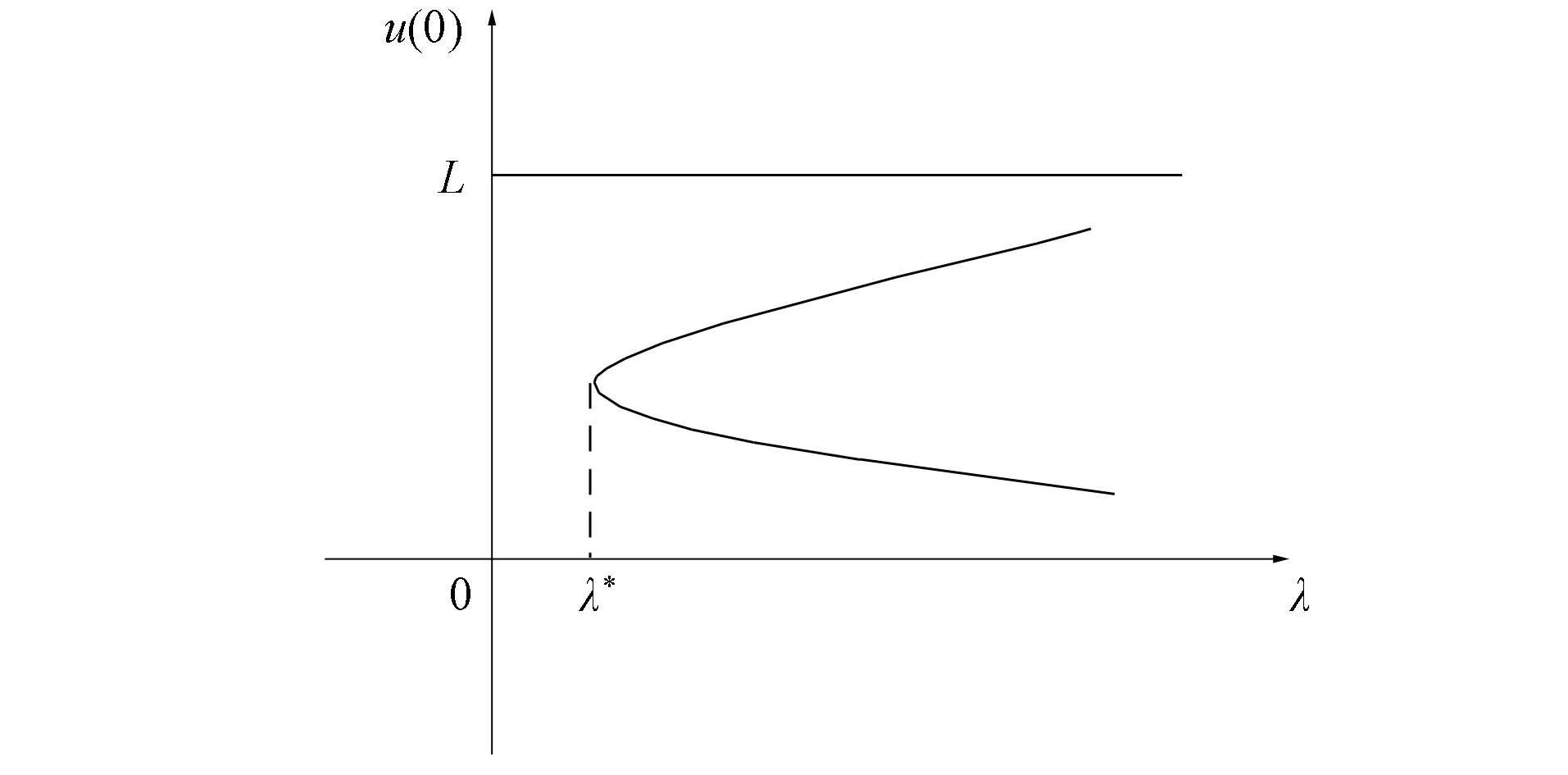
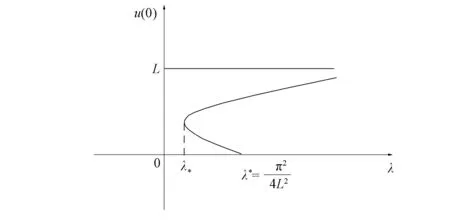
1)f∈C([0,∞),R),f(u)>0, 0 2)f∈C1([0,∞),R),f′(u)u≤f(u), 0 则有: 定理2[12]若f(u)=up(p>1), 则存在λ*>0, 使得当λ∈(0,λ*)时, 问题(4)无正解; 当λ=λ*时, 问题(4)恰有一个正解; 当λ∈(λ*,∞)时, 问题(4)恰有两个正解. 文献[15-17]研究表明, 拟线性问题与半线性问题有很多不同之处, 分歧图也不同.由于平均曲率问题的时间映像估计较复杂, 因此文献[12]只讨论了非线性项在零点处次线性增长的情形, 如f(u)=up(p>1),f(u)=up+uq(q>p>1).而对非线性项为f(u)=u(eu-1),f(u)=eu-1情形的研究目前尚未见文献报道.因此, 本文研究给定平均曲率方程Dirichlet问题(1)非线性项为这两种形式时正解的确切个数及分歧图, 其中参数λ>0,L>0.用时间映像原理获得了如下结果: 1) 当0<λ<λ*时, 问题(1)没有正解; 2) 当λ=λ*时, 问题(1)恰有一个正解; 3) 当λ>λ*时, 问题(1)有两个正解. 当f(u)=u(eu-1)时, 问题(1)的分歧图如图1所示. 1) 当0<λ<λ*时, 问题(1)无正解; 2) 当λ=λ*或λ≥λ*时, 问题(1)恰有一个正解; 3) 当λ*<λ<λ*时, 问题(1)有两个正解. 当f(u)=eu-1时, 问题(1)的分歧图如图2所示. 图1 当f(u)=u(eu-1)时问题(1)的分歧图Fig.1 Bifurcation diagram of problem (1) when f(u)=u(eu-1) 图2 当f(u)=eu-1时问题(1)的分歧图Fig.2 Bifurcation diagram of problem (1) when f(u)=eu-1 设u(x)是问题(1)的正解.由于u(x)在x=0处取得最大值并且关于x=0对称, 且当-L (5) 进而有 (6) 对式(6)两端从0到L积分, 可得 Tλ(s)称为f的时间映像.由时间映像的定义可知, 问题(1)等价于找到s∈(0,L), 使得 Tλ(s)=L. (7) (8) 引理1[12]若f: [0,+∞)→[0,+∞)是连续函数, 且∀u∈(0,L),f(u)>0, 则有 (9) (10) 引理2[12]若f: [0,+∞)→[0,+∞)是连续函数, 且∀u∈(0,L),f(u)>0, 则对任意s∈(0,L), 时间映像T关于λ严格递减. 引理3[12]f: [0,+∞)→[0,+∞)是连续函数, 且满足∀u∈(0,L),f(u)>0. 引理4f: [0,+∞)→[0,+∞)是连续函数, 且满足∀u∈(0,L),f(u)>0. 证明: 1) 若f(0)>0, 则当s→0时, 故 故 并且当s→0时, 有 于是 引理5[12]记η(λ)=inf{Tλ(s)|s∈(0,+∞)}, 则η(λ)在(0,+∞)上递减; 记ω(λ)=sup{Tλ(s)|s∈(0,+∞)}, 若ω(λ)≠∞, 则ω(λ)在(0,+∞)上递减. 引理6若f(u)=u(eu-1), 则对于任意的λ∈(0,+∞), 有 ξ=λ(F(s)-F(st))=λ(ses-es-s2/2-stest+est+s2t2/2), 则 ξ′=λ(f(s)-tf(st))=λ[s(es-1)-st2(est-1)], ξ″=λ(f′(s)-t2f′(st))=λ[(es+ses-1)-t2(est+stest-1)]. 令 A=ξ=λ(ses-es-s2/2-stest+est+s2t2/2), B=sξ′=λ[s2(es-1)-s2t2(est-1)], C=s2ξ″=λ[s2(es+ses-1)-s2t2(est+sest-1)], 又 其中s[A(2+A)]5/2>0, 则 因为 令g(s)=s3+(M-3)s2+2(3-M)s+2(M-3), (g(s)es)′=s3+Ms2>0, ∀M>0, esg(s)-estg(st)>0, 又因为 则 根据Taylor公式, 当s<1/(1-t)时, 有 则 对式(11)关于t求导, 可得 g′(s)=4t3s4-(3t2+2t+1)(2M+3)s3+12(M+1)ts2+2(3-M)s, g″(s)=12t2s4-(6t+2)(2M+3)s3+12(M+1)s2,g‴(s)=24s4t-6(2M+3)s3, 从而 f1(s)=-(t3+t2+t+1)(2M+3)s3+6(M+1)t2s2+2(1+t)(3-M)s+4M. 由于s3≤s2, 则有-(t3+t2+t+1)(2M+3)s3≥-(t3+t2+t+1)(2M+3)s2, 于是 -(t3+t2+t+1)(2M+3)s3+6(M+1)t2s2≥[-(t3+t2+t+1)(2M+3)+6(M+1)t2]s2, g1(t)=-(t3+t2+t+1)(2M+3)+6(M+1)t2=-(t3+t+1)(2M+3)+(4M+3)t2, 当M=7,s∈(0,0.8)时, 式(12)大于0.下面证明 (t-1)2s2es(1+t)[(t2+4t+1)s2-2(M+3)(t+1)s+4M]>0. 令h=(t2+4t+1)s2-2(M+3)(t+1)s+4M, 可知 h′(t)=(2t+4)s2-2(M+3)s,h″(t)=2s2>0, 则h′(t)单调递增, 当t=1时,h′(t)=(2t+4)s2-2(M+3)s<0, 故h(t)单调递减.于是 h(t)=(t2+4t+1)s2-2(M+3)(t+1)s+4M≥6s2-4(M+3)s+4M, 引理7若f(u)=eu-1, 则对于任意的λ∈(0,+∞), 有 证明: 记ξ=λ(F(s)-F(st))=λ(es-est-s+st), 则 ξ′=λ(f(s)-tf(st))=λ(es-test-1-t), ξ″=λ(f′(s)-t2f′(st))=λ(es-t2est). 令A=λ(es-est-s+st),B=λ(ses-stest-s+st),C=λ(s2es-s2t2est), 可知 其中 g(s)=2(2+M)-8M+2s2-6s+2s(2+M)=2s2+2(M-1)s+4-6M, (g(s)es)′=[2s2+2(M+1)s+2-4M]es. 从而当0≤M≤1/2时, esg(s)-estg(st)≥0, 其中 令 由时间映像的定义可知, 问题(1)等价于找到s∈(0,L), 使得 T(s)=L. (13) 因此当非线性项为f(u)=u(eu-1)时, 问题(1)的解等价于方程(13)的解. (14) 由时间映像的定义可知, 问题(5)等价于找到s∈(0,L), 使得式(13)成立.因此当非线性项为f(u)=eu-1时, 问题(1)的解等价于方程(13)的解. (15)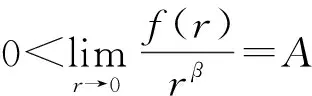
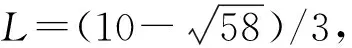
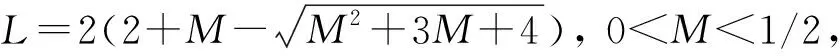
2 预备知识
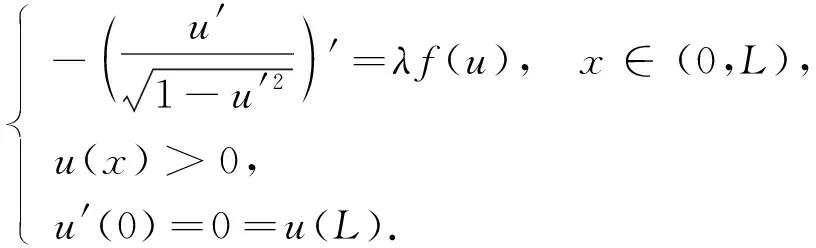
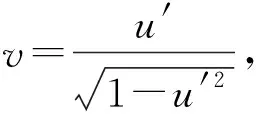
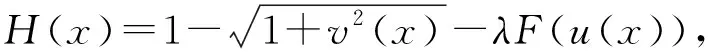
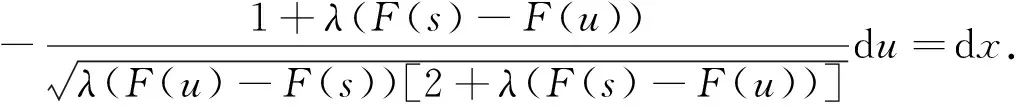
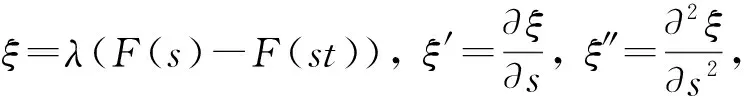
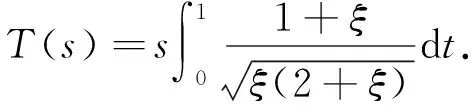
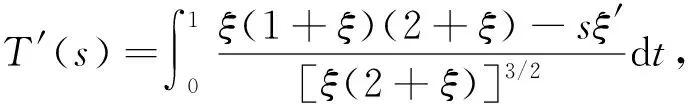
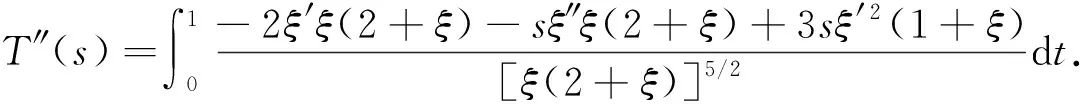


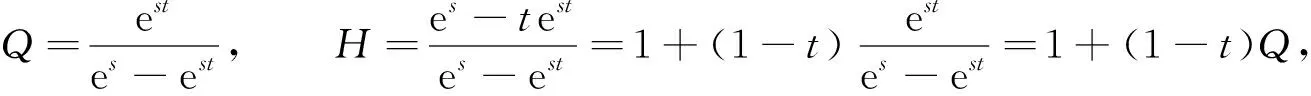
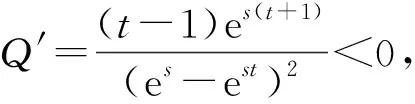
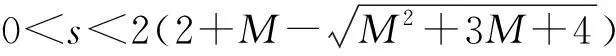
3 主要结果的证明
3.1 定理3的证明
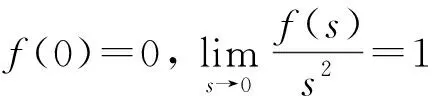
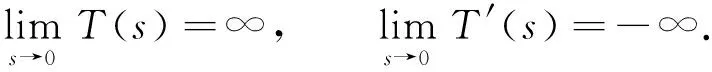
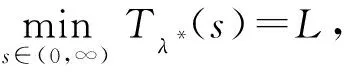
3.2 定理4的证明