抛物线定义在无理函数最值的应用演绎

王淼生 叶建聪

（1.厦门第一中学，福建 厦门 361003；2.福建教育学院数学教育研究所，福建 福州 350025；3.厦门市五显中学，福建 厦门 361100）

抛物线作为圆锥曲线“大家庭”中的一员，其定义在很多方面有突出表现.以下通过三个具体案例，凸显抛物线定义在无理函数最值（最大值、最小值）上的精彩应用，彰显抛物线（圆锥曲线的精髓）的精髓——数形结合思想：以数构形，由形助数.

一、案例呈现

构造点A(2,3)，B(1,0)，P(x2,x)，则上式表明f(x)max就是|PA|-|PB|的最大值.

事实上，动点P(x2,x)的轨迹方程为y2=x（之所以配方就是为了构造抛物线），即在抛物线y2=x上寻找点P，使得|PA|-|PB|有最大值，如图1 所示.观察图1 易得：

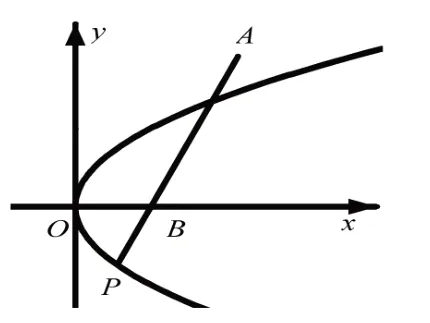
图1

此时，线段AB的延长线与抛物线y2=x的交点正是满足题意的点P.

解法2：其实，还可以将函数f(x)的表达式适当变形为：

构造点C(3,2)，D(0,1)，Q(x,x2)，则上式表明f(x)max就是|QC|-|QD|的最大值.

事实上，动点Q(x,x2)的轨迹方程为x2=y，即在抛物线x2=y上寻找点Q，使得|QC|-|QD|的最大值，如图2 所示.观察图2 可得：

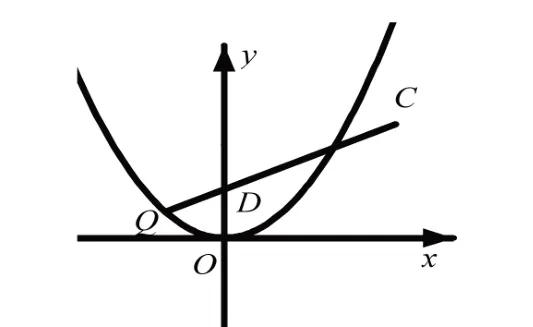
图2

此时，线段CD的延长线与抛物线x2=y的交点正是满足题意的点Q.

解：函数g(x)表达式后半部分的根号表示动点P(x,x2)与定点之间的距离|PA|.动点P的轨迹为准线l方程为、焦点为的抛物线x2=y，定点A为该抛物线外一定点.函数g(x)表达式前半部分“x2”的含义即为动点P到x轴的距离|PB（|B为垂足），如图3 所示.据此可知g(x)=|PB|+|PA|.观察图3 可得：

图3

依据抛物线定义可得|PC|=|PF|，于是得到

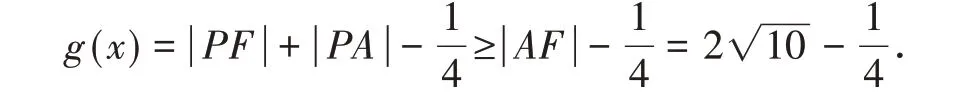
此时，线段AF与抛物线x2=y的交点正是满足题意的点P.

解：依据两点间距离公式，不难发现函数h(x,y)表达式前半部分的根号表示动点P(x,lnx) 与动点之间的距离|PQ|，而动点P(x,lnx)在曲线y=lnx上运动，动点在准线l方程为y=-1、焦点为F(0,1)的抛物线x2=4y上运动.函数h(x,y)表达式后半部分就是抛物线上的动点Q的纵坐标，即为Q到x轴的距离|QN|（N为垂足），如图4 所示.据此可知h(x,y)=|PQ|+|Qn|.观察图4 可得

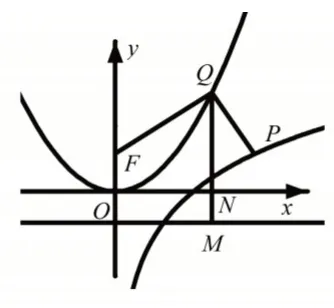
图4

依据抛物线定义可得|QM|=QF，于是得到

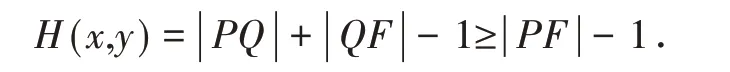
这表明h(x,y)最小值取决于F到曲线y=lnx上的动点P之间距离的最小值.

再一次利用两点间距离公式得到|PF|=

构造函数φ(x)：φ(x)=x2+(hnx-1)2，则有φ(x)=

再构造函数ω(x)：ω(x)=x2+lnx-1，则有

因x∈(0,+∞)，则ω(x) ＞0 恒成立，即ω(x) 在x∈(0,+∞) 为单调增函数.当x→+∞ 时，ω(x) →+∞；当x→0+时，ω(x) ＞0.注意到ω(1)=0，则当x∈(0,1)时，ω(x) ＜0；当x∈(1,+∞)时，ω(x) ＞0，也就是说x∈(0,1) 时，φ(x) ＜0；当x∈(1,+∞) 时，φ(x) ＞0，于是φ(x)在x∈(0,1)上为单调减函数，φ(x)在x∈(1,+∞)上为单调增函数，则φ(x)min=φ(1)=2，即故h(x,y)min=此时，R(1,0)正是满足题意的点P.

当然，作为填空题，可以借助图形直观性直接看出|PF|的最小值.因为曲线y=lnx在点R(1,0)处的切线方程为y=x-1，而此时直线FR的方程为y=1-x，恰好这两条直线相互垂直，如图5 所示，因此|PF|的最小值就是即1，此时R就是满足条件的点P.

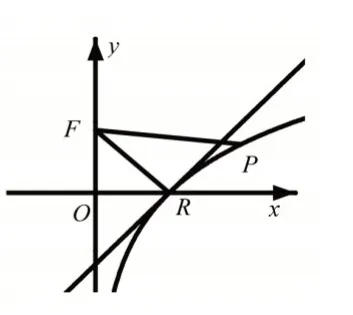
图5

值得特别说明的是：案例2、案例3 均可以类似于上述案例1 中的解法2 那样，将函数g(x)与h(x,y)的表达式分别变形为：

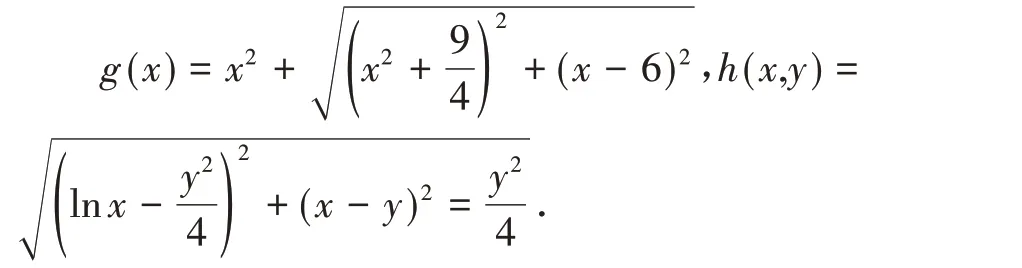
请读者模仿案例1 中的解法2 的过程，自行推理.

二、回顾反思

案例1 是一道竞赛题.f(x)表达式中不仅含有与而且根号里面均为高次.即使移项、平方去掉根号也难以处理，因此需要将f(x)表达式适当变形.变形的本质就是构造抛物线的过程，为借助抛物线定义解决问题奠定基础.

案例2 由名校自主招生改编而来g(x)表达式含有根号而且根号里面已经配方，似乎比案例1 简单，其实不然.因为案例1 中两个根号经过适当变形后，可以看作同一个动点到两个定点距离之差（几何意义），而案例2 中根号与前半部分“x2”仅从表面上很难发现其内在的几何意义.学生普遍害怕案例2 这类试题.

案例3 源自高三模拟考填空题压轴题.相比案例2，h(x,y)表达式显得更为复杂.尽管学生能够理解几何意义，即为点P(x,lnx)与点之间的距离.但这是两个动点，而且学生难以构建后半部分之间的“桥梁”，导致前功尽弃，很少学生得到正确答案.

三、心得体会

涉及无理函数的最值问题，需要特别关注表达式外部结构特征，常常通过恰当配方，借助两点间距离公式，实现等价转化，凸显几何背景，顺势构造相关图形（尤其圆锥曲线），渗透数形结合思想，利用圆锥曲线定义与性质，往往能找到最佳的解决方法.以数构形，由形助数，将逻辑推理、数学运算与直观想象等核心素养演绎得淋漓尽致.在享受数学简洁之美的同时，对培养数学兴趣、优化思维品质、发展学生智力、激发创造能力大有裨益.

圆锥曲线是一个和谐的“大家庭”，抛物线只是圆锥曲线“大家族”中的一员，因此在处理综合性较强的问题时，常常需要将抛物线与椭圆、双曲线乃至圆、直线、点等相关定义、性质“强强联手”，交辉相应，从而演绎整个圆锥曲线的精彩应用.事实上，抛物线、椭圆、双曲线定义在其他很多方面同样有精彩的演绎（比如文［1］、文［2］、文［3］等）.以上案例仅仅只是管中见豹，意在抛砖引玉，期盼同行有更多的研究成果.