基于模板匹配的快速位移提取算法研究

朱春丽,雷秀军,申 远

(1.合肥师范学院 电子信息系统仿真设计安徽省重点实验室，安徽 合肥 230601；2.合肥富煌君达高科信息技术有限公司，安徽 合肥 230031)

随着摄像技术和图像处理技术的发展，视觉测量技术引起了人们的关注，它具有非接触式、远距离测量、测量范围大、测量精度高和价格便宜等优点，且无附加质量，不会对测量物体的动态特性产生影响[1-3]。视觉测量技术利用相机拍摄物体的运动视频，并使用数字图像处理技术对视频图像分析、处理，从而实现物体的运动估计[4-6]。对于物体的运动估计，除了需要具备一定的硬件设备之外，还要具有高速、高精度、鲁棒性的图像匹配算法。其中模板匹配是图像处理中最基本、最常用的匹配方法，在机器视觉中有着广泛的运用。早期的模板匹配主要应用于遥感图像的配准[7]，现阶段已广泛应用于智能交通、视频监控、目标跟踪、视觉检测以及人机交互等[8-10]。

一般来说，可以用多种方法获得物体的运动信息，但为了实现较优的模板匹配，需要得到一个标量值作为匹配结果，再使用相关函数计算匹配结果即可得到运动的提取结果。本文以零均值归一化标准互相关准则(Zero-normalized Cross-correlation,ZNCC)作为模板匹配的评价标准。由于归一化因子的存在，ZNCC准则的计算结果在[-1,1]范围内，能够直观显示模板匹配的效果和可靠性，并能够进行更深一步的计算，还能够完美地避开光照和噪声所产生的干扰，鲁棒性很强，因而，针对运动估计的图像匹配，尤其在有光照变化等干扰存在的情况下，ZNCC反而是首选[11]。常用的基于模板匹配的位移提取算法有全局搜索(Full Search, FS)算法等[12-13]，本研究以ZNCC准则作为模板匹配的评价标准，以做较大位移为主的椭圆和较小位移为主的螺旋线两种运动的灰圆为计算示例，对以上四种位移算法的提取精度和速度进行了比较分析。

模板匹配通过比较两幅数字图像之间的偏移从而获得位移信息，无法满足实际测量的高精度要求。另一种解决方案是改进位移提取算法的定位精度，该方法简单、有效且成本低。在结构动态测量中，要求位移算法具有高响应速度和高精度的特点，因此，在上述基于模板匹配的快速位移提取算法中引入曲面拟合法和梯度法两种常用的亚像素定位方法[14-15]，并对其定位性能进行了比较分析。基于模板匹配的快速、高精度位移提取算法简单、有效且成本低，对于实际应用中的动态运动估计具有一定的参考价值。

1 算法简介

1.1 FS算法

FS是一种搜索精度很高的算法，步骤如下：

(1)以ZNCC为匹配准则，从搜索区域的中心点开始，按照由近及远的顺序，计算目标图像中每个像素点与模板图像的相关值CZNCC(xi,yi)；

(2)对比CZNCC(xi,yi)的大小，找到最大相关值所对应的位置，则该位置即为所求的最佳匹配位置。

1.2 TSS算法和NTSS算法

TSS算法采用渐进的搜索模式来寻找最佳匹配位置，具体搜索步骤如下：

(1)以ZNCC为匹配准则，以搜索范围的一半为搜索步长，对于搜索区域的中心点以及与其相距距离为步长的8个点，从中心点开始，计算这9个点与模板图像的相关值CZNCC(xi,yj)，对比CZNCC(xi,yj)的大小，找到最大相关值所对应的位置；

(2)以上一步步长的一半为搜索步长，以上一步找到的最大相关值所对应位置作为新的中心点，对于新的中心点以及与其相距距离为步长的8个点，从中心点开始，计算这9个点与模板图像的相关值CZNCC(xi,yj)，对比CZNCC(xi,yj)的大小，找到最大相关值所对应的位置；

(3)重复步骤2，直到步长减少到1，此时，最大相关值所对应的位置即为所求的最佳匹配位置。

TSS算法不需要遍历目标图像中的所有像素点，搜索效率远高于FS算法，但第一步搜索步长较大，采用固定的搜索路径进行搜索，易陷入局部最优，对静止或微小位移的提取效果不好。于是，提出了具有自适应的NTSS算法，其改进之处如下：

(1)搜索点除了中心点以及与其相距距离为步长的8个点之外，还要增加搜索区域中心点的8邻域点；

(2)对于静止或者微小位移的提取：若最大相关值在中心点处，则停止搜索；若最大相关值出现在中心点的8邻域，则以最大相关值所对应位置作为新的中心点，计算新中心点的8邻域，找出最大相关值，重复以上步骤，直到最大相关值出现在新的中心点处；

(3)对于相对较大位移的提取：最大相关值出现在与搜索中心点相距距离为步长的8个点处，执行TSS算法的步骤2和步骤3。

对于相对较大位移的搜索路径，NTSS算法和TSS算法的搜索原理一致。此外，它还兼顾了静止或微小位移的提取。

1.3 DS算法

不同于TSS算法所采用的固定搜索路径，DS算法针对相对较大位移和静止或者微小位移的提取，采用大范围搜索(搜索9个点)和小范围搜索(搜索5个点)两种搜索路径，搜索过程稳定，且不易陷入局部最优。DS算法的具体搜索步骤如下：

(1)以ZNCC为匹配准则，从搜索区域的中心点开始，进行大范围菱形搜索，若最大相关值在中心点处，执行步骤3，否则执行步骤2；

(2)以上一步找到的最大相关值所对应位置作为新的中心点，进行大范围菱形搜索，若最大相关值在新的中心点处，执行步骤3，否则重复执行步骤2；

(3)以上一步找到的最大相关值所对应位置作为新的中心点，进行小范围搜索，找到最大相关值所对应的位置，则该位置即为所求的最佳匹配位置。

1.4 曲面拟合法

进行模板匹配时，最大相关系数点(整像素点)附近为一光滑曲面，该曲面的极值点所在位置即为图像的最佳匹配位置。因此，可以利用相关系数矩阵拟合曲面，然后计算曲面函数的极值点，从而得到亚像素等级的位移估计。

实际应用于位移估计时，为了减少计算量，本文选择最大相关系数点及其周围的8个点进行曲面拟合。由于曲面变化较为平缓，采用二元二次多项式拟合曲面。具体步骤如下：

(1)用二元二次多项式拟合曲面，拟合窗口大小选为3×3，获得9个等式；

(2)用最小二乘法完成该二次曲面系数的求解；

(3)对二次曲面函数进行微分，求出曲面极值点的位置。

1.5 梯度法

基于梯度的亚像素定位算法最早是由 Davis 等提出的[15], 其基本思想是假设图像平移前后没有发生变化。利用基于梯度的亚像素位移算法求解位移时只需要计算出模板图像的灰度梯度，相对来说易于实现。

2 结果

2.1 计算示例

为了防止出现局部最优等现象干扰对FS、TSS、NTSS、DS四种算法计算精度和速度的判断，采用相关函数分辨特性较好的灰圆作为计算示例。另外，为了比较四种位移提取算法对不同位移尺度的适应性，令灰圆做不同位移尺度的运动，这里令其作较大位移尺度为主的椭圆运动和较小位移尺度为主的螺旋线运动，运动周期为2 s，运动轨迹如图1中的深色路线所示。

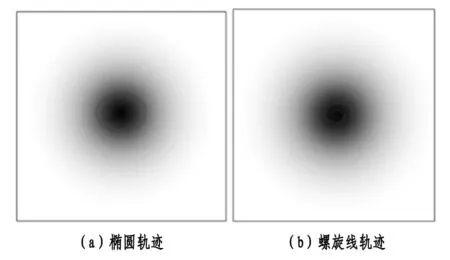
图1 圆模板的运动轨迹图

2.2 四种位移提取算法的对比分析

灰圆模板作较大位移为主的椭圆运动时，搜索区域是以圆心为中心，范围为[-15像素,15像素]的方形区域。四种搜索算法提取出的灰圆沿x和y方向的位移矢量如图2所示，可以看出四种搜索算法的提取结果基本重叠，均能较好地提取出灰圆的运动轨迹。另外，通过比较提取的位移矢量和灰圆的运动轨迹，发现每一种搜索算法的计算精度均在[-0.5像素，0.5像素]之间。因为基于相关函数进行模板匹配时，计算精度为像素量级，四种搜索算法均采用ZNCC准则，因此从理论上来讲，它们的计算精度等级都是一样的，和图2所示的计算结果相一致。

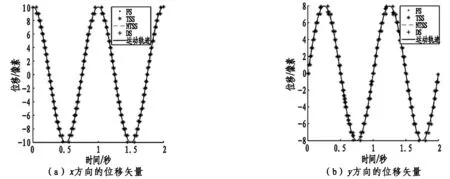
图2 利用四种搜索算法提取椭圆轨迹

四种搜索算法均采用ZNCC准则，采用不同搜索算法计算一个像素点的相关值所需的时间是相同的，因此可以用提取位移信息整个过程所需搜索的点数来评价计算速度。FS算法对目标图像中的所有像素点进行相关性运算，所需要搜索的点数远远大于其它几种搜索算法，计算速度最慢，下面将不再作统一比较。随着灰圆作椭圆运动时间的增加，TSS、NTSS、DS三种搜索算法所需的搜索点数如图3所示。可以看出，随着灰圆作椭圆运动时间的增加，TSS和NTSS算法的搜索点数均不变，DS算法的搜索点数剧烈变化。

图3 利用三种搜索算法提取椭圆轨迹所需的搜索点数

另外，NTSS算法的搜索点数大于TSS算法，DS算法的平均搜索点数也大于TSS算法，因为在TSS算法的基础上，NTSS算法还兼顾了静止或微小位移的提取，DS算法针对相对较大位移和静止或者微小位移的提取，采用了大范围搜索和小范围搜索两种搜索路径。对于位移较大的椭圆运动，NTSS和DS算法会浪费一些搜索时间，TSS算法反而是最适合的搜索方法。

为了验证运动轨迹以小位移为主时四种算法的适应性，本文计算了灰圆模板作小范围螺旋线运动时的位移提取结果和搜索点数。相对于较大位移为主的椭圆运动，缩小了螺旋线轨迹的运动范围和搜索范围，搜索区域是以圆心为中心，范围为[-7像素,7像素]的方形区域，四种搜索算法提取出的灰圆沿x和y方向的位移矢量如图4所示。同样，四种搜索算法均能较好地提取出灰圆的运动轨迹，且计算精度均在[-0.5像素,0.5像素]之间。

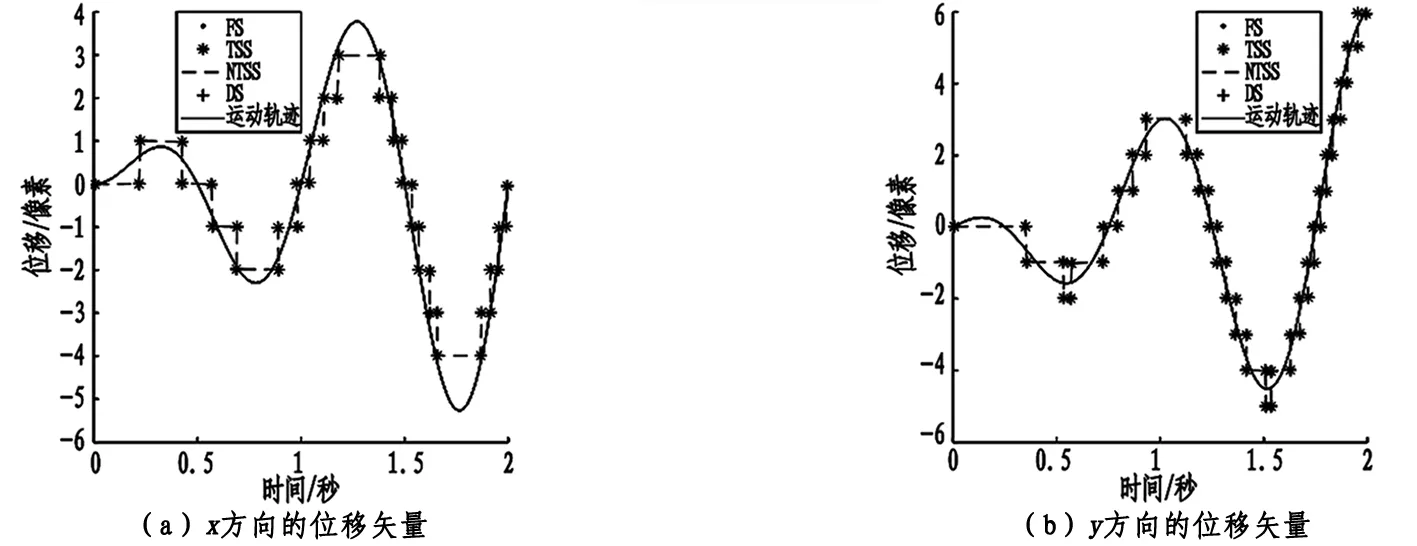
图4 利用四种搜索算法提取螺旋线轨迹

随着灰圆作螺旋线运动时间的增加，TSS、NTSS、DS三种搜索算法所需的搜索点数如图5所示。

图5 利用三种搜索算法提取螺旋线轨迹所需的搜索点数

可以看出，随着灰圆作螺旋线运动时间的增加，TSS算法的搜索点数不变，均为33个点。对于NTSS算法，位移较小的一段时间内，搜索点数为17，位移逐渐增大的一段时间内，搜索点数增加为25，位移更大时，搜索点数便大于TSS算法了，与大范围椭圆运动时的结果一致。对于DS算法，搜索点数依然波动剧烈，但平均来看，在位移较小的一段时间内，搜索点数远小于TSS和NTSS算法，位移逐渐增大后，搜索点数与TSS算法相当。因此，对于小位移为主的螺旋线运动，DS算法更为合适。

2.3 亚像素位移测量算法的性能比较

同样以灰圆作为仿真对象，使其做步长为0.05像素的平移运动，位移范围为[-0.5像素，0.5像素]。为了看清楚模板大小对精度和效率的影响，选择了三种计算模板，大小分别为 21像素×21像素、51像素×51像素和81像素×81像素，两种算法的平均计算误差如表1所示。

由表1可以看出，模板较小时，曲面拟合的误差远大于梯度法的误差，随着模板的增大，两种算法的定位误差均逐渐减小，且差别也越来越小。

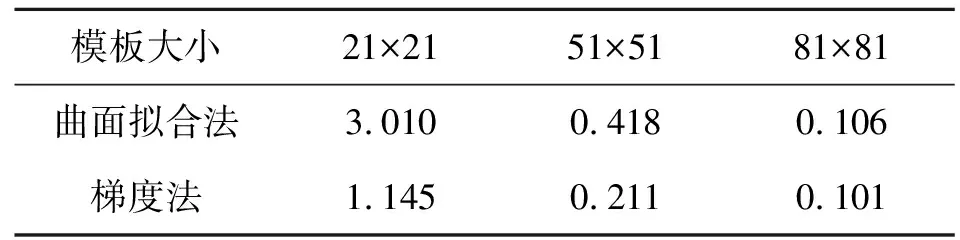
表1 两种亚像素定位算法的平均计算误差(×10-3像素)

为了获得亚像素精度的位移结果，需在原有基于模板匹配的位移提取算法基础上，加上亚像素定位算法。在此，只比较加上亚像素定位算法之后，位移提取算法额外增加的计算时间，统计结果如表2所示。曲面拟合法额外增加的时间便是拟合曲面和计算极值所需的时间，从表2可以看出，该时间与模板大小无关，均为0.007 s。梯度法额外增加的时间便是求解目标函数梯度和亚像素位移所需的时间，可以看出，计算时间远远大于曲面拟合法额外增加的计算时间，且随着模板的增大而增大。

表2 两种亚像素定位算法额外增加的计算时间 s

实际应用中，需综合考虑算法精度和计算时间，因而曲面拟合法更加适用。在基于模板匹配的DS位移提取算法基础上，利用曲面拟合法求解图1(b)中灰圆的螺旋线运动，其中模板大小为51×51像素，y方向的位移矢量结果如图6所示。可以看出，利用DS算法的提取结果呈阶梯状，误差大小为[-0.5像素，0.5像素]，加上曲面拟合算法之后，位移结果能够比较完美的接近实际运动曲线。

图6 利用曲面拟合法提取螺旋线y方向位移矢量的结果

3 结论

以作椭圆和螺旋线两种运动的灰圆模板为计算示例，比较分析了基于模板匹配的FS、TSS、NTSS、DS四种搜索算法对位移信息的提取精度和速度的影响。四种搜索算法均以ZNCC为匹配准则，计算精度一样，均为像素量级。FS算法要遍历目标图像中的每一个点，最为耗时，不适合解决实际应用中的实时性问题。TSS、NTSS、DS三种搜索算法的搜索速度均远远超过了FS算法，可分别适用于解决不同实际应用中的实时性问题。TSS算法采用渐进的搜索模式来寻找最佳匹配位置，但TSS算法的第一步搜索步长较大，采用固定的搜索路径进行搜索，易陷入局部最优，对静止或微小位移的提取效果不好，适于范围较大位移的提取。NTSS算法具有自适应性，它在TSS算法的基础上，还兼顾了静止或微小位移的提取，相对于TSS算法，更适于小位移存在的运动估计。DS算法针对相对较大位移和静止或者微小位移的提取，采用大范围搜索和小范围搜索两种搜索路径，搜索过程稳定，是搜索性能最为优异的快速匹配算法之一，对于小位移为主的运动估计，DS算法最为合适。为了获得亚像素级的定位精度，本文还比较分析了常用的曲面拟合法和梯度法两种亚像素定位算法的性能。在原基于模板匹配的位移提取算法基础上，曲面拟合法额外增加的时间便是拟合曲面和计算极值所需的时间，远小于梯度法额外增加的时间。实际应用中，综合考虑算法精度和计算时间，曲面拟合法更加适用。本文的比较分析结果对基于视觉的实际运动估计的算法选择具有一定的参考价值。