基于矩阵法的无节奏流水施工优化技术研究

石振庆，朱恩赐

(滁州学院 土木与建筑工程学院，安徽 滁州 239000)

流水施工是将拟建施工项目在竖向分为多个施工层，在水平方向上分为多个施工段，按施工工艺组成相关施工队进行施工，最后根据预先计划，按次在各施工层和各施工段上施工的组织方法。依据流水的节奏规律性可分为有节奏流水和无节奏流水[1]。在实际工程中，由于各个施工队的工作效率和各施工层、段上的工作量不能完全相同，从而造成工程项目流水节拍的差异，故此时有节奏流水不再适用，必须组织可使每个专业施工队连续施工的无节奏流水施工。正因无节奏流水施工更符合实际施工过程中所遇各种复杂情况，故无节奏流水在实际施工中更为普遍[2]。同时它的一致性还主要体现在与当今土木工程实际项目需求一致，方便了工程项目的管理，提高了施工效率。对无节奏流水工期优化方法的研究具有一定的研究价值和研究前景，对施工企业在优化工期上具有一定的参考意义。

1 无节奏流水施工工期的计算方法

计算工期时，首先需知全部施工过程在各施工段上的流水节拍t，然后用已知流水节拍t求解出所有分项工程间的流水步距K，再确定各施工过程之间的间隙时间Z，最后根据计算公式将上述求解的各个参数代入式中得到最终工期。

1.1 流水步距的计算

流水步距的计算方法常用“潘特考夫斯基法”[3]，其方法步骤是对各施工过程在各施工段上的流水节拍依次累加，将得到各施工过程流水节拍的累加数列进行错位相减，然后取最大值，即为相邻两个施工过程的流水步距。

例1 一项工程由A、B、C3个施工过程组成，该项工程分成4个施工段进行施工，根据相关规范规定，施工过程B完成后需要养护2天，工程项目组织无节奏流水施工，各施工段流水节拍如表1所示，计算流水步距。

表1 各施工段流水节拍

(1)将三个施工过程的流水节拍依次累加形成数列。

(2)对上述求得的数列错位相减。

KAB:

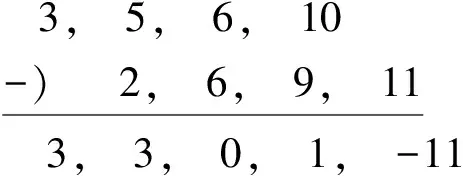
KBC:

(3)确定KAB、KBC。

对所有结果取最大值，得到了AB施工过程间的流水步距KAB=3，BC施工过程间的流水步距KBC=4。

1.2 无节奏流水施工工期的计算

无节奏流水施工工期的计算公式为：

T=∑Ki,i+1+tn+∑Z1+∑Z2+∑D

(1)

式中T表示无节奏流水施工工期；∑Ki,i+1表示第i个施工过程与第i+1个施工过程之间的流水步距和；tn表示最后一项施工过程所使用的全部时间；∑Z1表示工艺间隙时间和；∑Z2表示组织间隙时间和；∑D表示搭接时间和。

继例1：

(1)根据相关规范规定，施工过程B完成后需要养护2天；

(2)最后一个施工过程的持续时间tn=4+1+3+3=11(天)；

(3)1.1节中计算得到流水步距KAB=3、KBC=4；

(4)将所有数据带入工期的计算公式；

T=∑Ki,i+1+tn+∑Z1+∑Z2+∑D=3+4+11+2=20(天)；

(5)绘制无节奏流水施工计划图如图1所示。

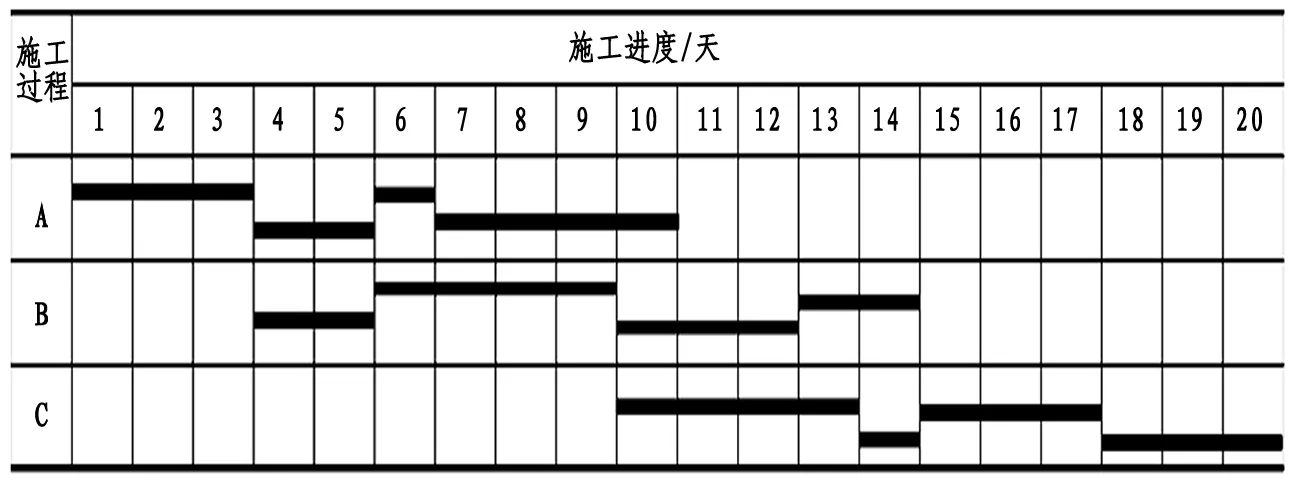
图1 无节奏流水施工计划图

2 利用矩阵法优化无节奏流水工期

上述计算工期的过程默认了施工段的最初排序，在不考虑其他因素的情况下，无节奏流水施工的工期主要受施工段不同的排序影响，施工段排序的不同会造成相邻施工过程流水步距和的不同，从而影响工期。本文主要研究如何运用矩阵法求解最优施工段顺序，从而达到流水步距和工期最小的目的。

2.1 矩阵法的原理分析

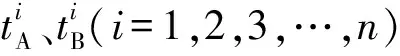
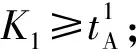
在“潘特考夫斯基”法的基础上，矩阵法认为工期受间隙时间的影响，因为各施工段的顺序不同导致施工过程的间隙时间不同。矩阵法通过引入两个参数排序流水步距和排序间隙时间，绘制出排序间隙时间矩阵表，根据排序间隙时间矩阵表，进而找出最优施工段顺序，使得各施工过程的间隙时间和最小，从而达到减少工期的效果。

2.2 矩阵法的应用

矩阵法的具体应用步骤如下：

(1)矩阵法引入了两个参数[4]：排序流水步距K′和排序间歇时间Z′，计算公式如下：

(2)

(3)

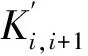
(2)运用上述公式，求出排序流水步距K′和排序间歇时间Z′。

(3)根据第二步计算结果建立排序间歇时间矩阵表。

(4)施工段最优排序的确定：首先将排序间隙时间矩阵表纵列求和；其次将排序间隙时间最小的施工段选出暂不进行排序；再对剩余各个施工段所要使用的时间进行对比，选择使用时间最短的两个施工段，按顺序比较两施工段施工过程的流水节拍，将流水节拍小的排在第一位，流水节拍大的排在最后一位；尽量把使用时间最长的施工段放在中间位置；最后再把剩余的施工段进行排序[5]。

2.3 矩阵法优化工期的应用

仍以例1举例：

(1)首先根据2.1节中矩阵法两个参数流水步距K′和排序间歇时间Z′的公式进行求解。施工段1与施工段2组合(如表2)：

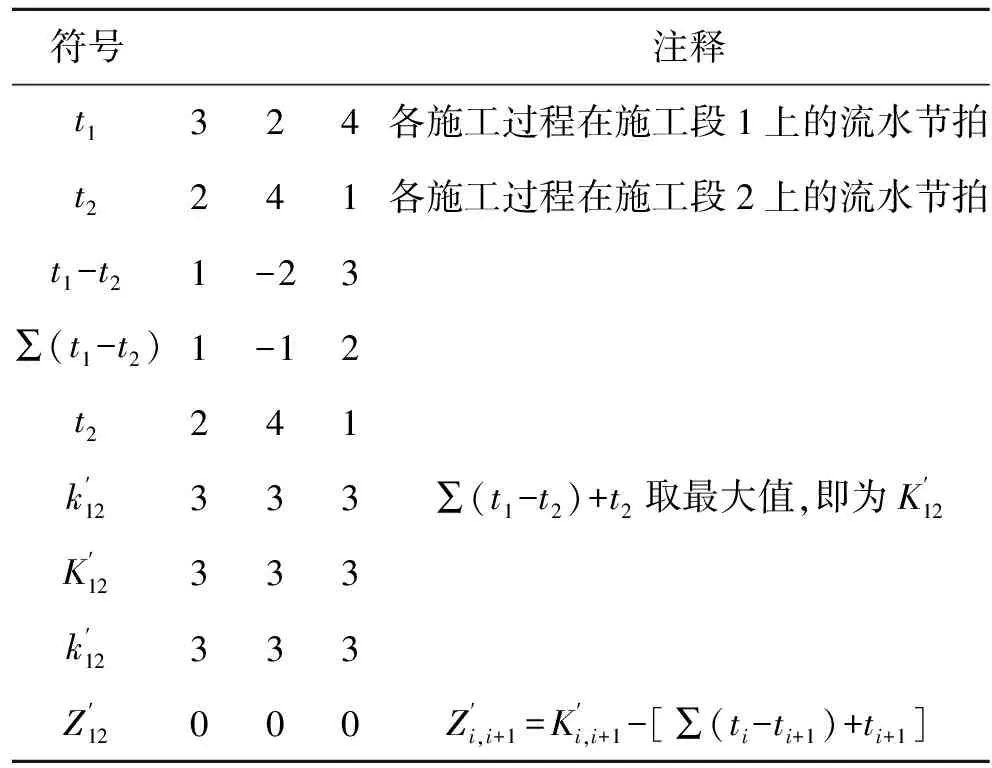
表2 施工段1和施工段2计算流程表

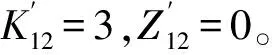
(2)绘制排序间隙时间Zij矩阵表(见表3)：

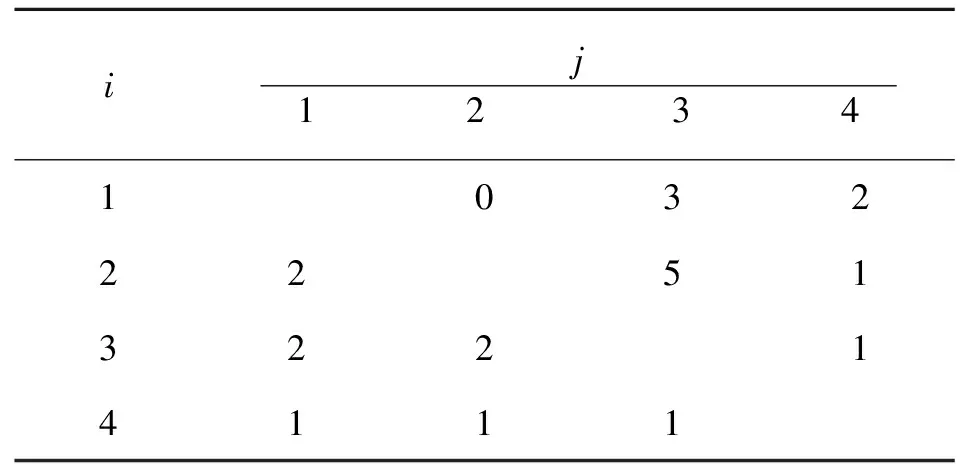
表3 排序间隙时间矩阵表

(3)根据2.1节中的第三步，可以确定最优施工段的顺序为3→1→4→2。

(4)根据最优的施工段顺序(见表4)，进行工期的计算。

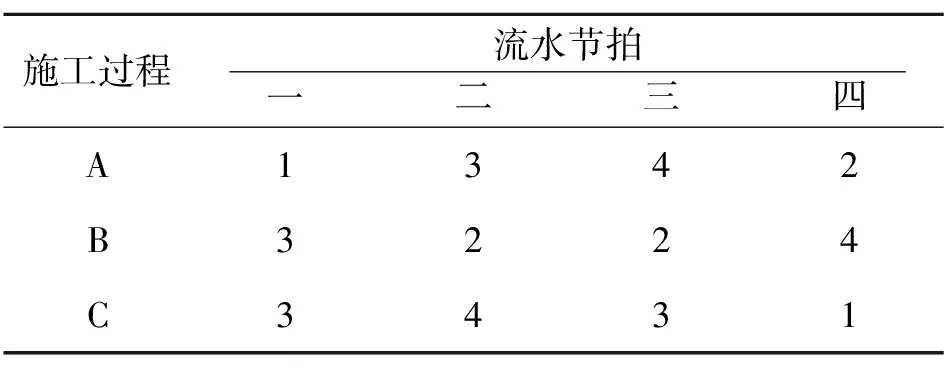
表4 优化后的各施工段的流水节拍

(5)求施工过程A、B、C之间的流水步距。

KAB:

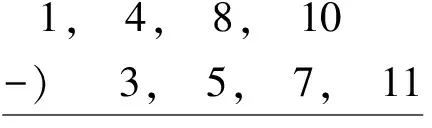
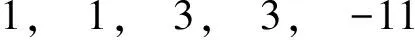
KBC:

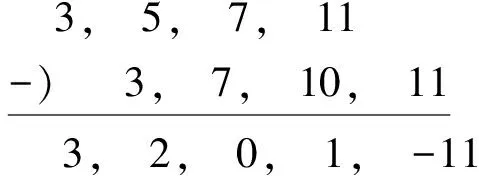
所以KAB=3，KBC=3。

(6)将所有数据带入工期的计算公式。

T′=∑Ki,i+1+tn+∑Z1+∑Z2+∑D=3+3+11+2=19(天)；

(7)优化后的工期比优化前节省了1天。

(8)绘制无节奏流水施工计划图(如图2)。

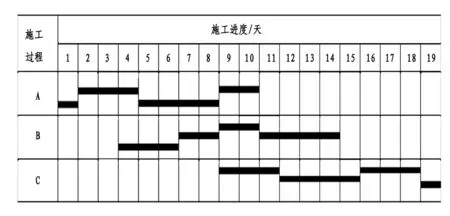
图2 无节奏流水施工计划图

3 实例分析

3.1 工程概况

某综合实验楼工程基地面积23855.53m2，建筑占地面积6182.68m2，总建筑面积42736.49m2。其中地上面积36899.84 m2，地下建筑面积5836.65 m2。设计使用年限50年。本项目为二类高层民用建筑，建筑耐火等级二级，地下室建筑耐火等级一级，屋面防水等级一级，地下室防水等级二级。主要结构类型为钢筋砼框架结构，建筑地上7层，地下1层，建筑高度30.70 m(室外地坪至平屋面)，地下埋深5.85 m。抗震设防烈度6度。本项目设地下人防工程，战时为甲类防空地下室，抗力级别为常6级，核6级，防化级别为丙级的二等人员掩蔽所。

3.2 某综合实验楼工期优化

(1)施工进度计划和保障措施。

进度要求：在保障安全质量的条件下，采用全新工艺和管理体系，确保本工程工期不高于285个日历天。

(2)初步计划施工流水段上的流水节拍见表5，初步计划施工进度计划图见图3。

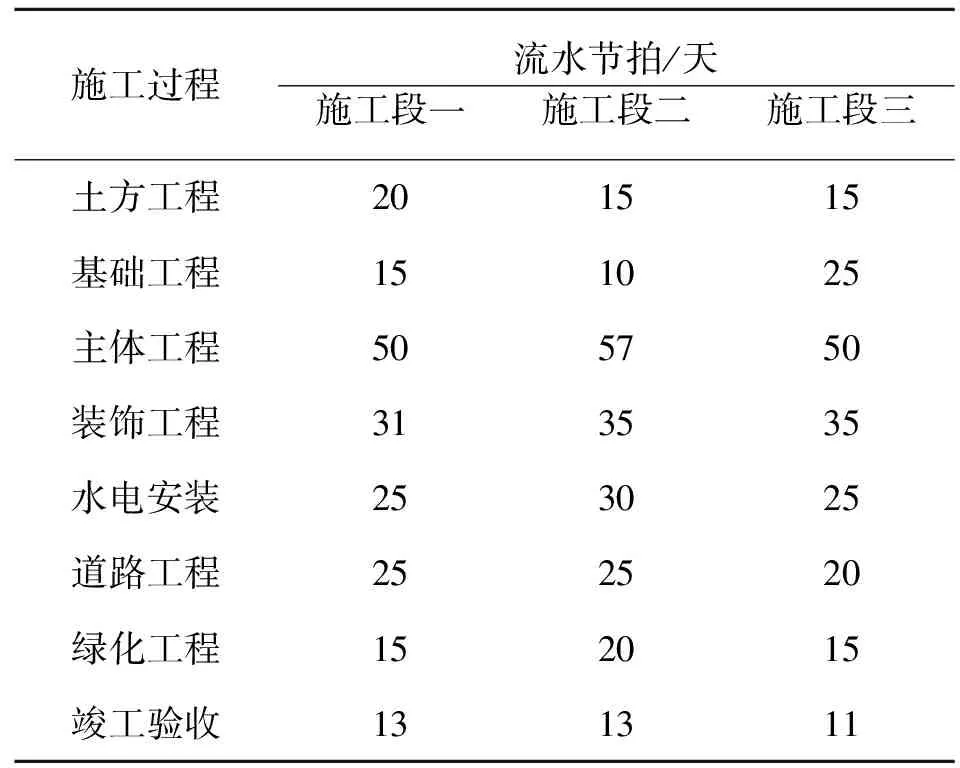
表5 初步计划施工流水段上的流水节拍

图3 初步计划施工进度计划图

(3)已知土方工程完成后，工艺间隙时间为3天；基础工程完成后，工艺间隙时间为7天；主体工程完成后，工艺间隙时间为7天；道路工程完成后，组织间隙为2天。

(4)根据初步计划，对工期利用矩阵法进行优化处理，施工段1与施工段2组合(见表6)：

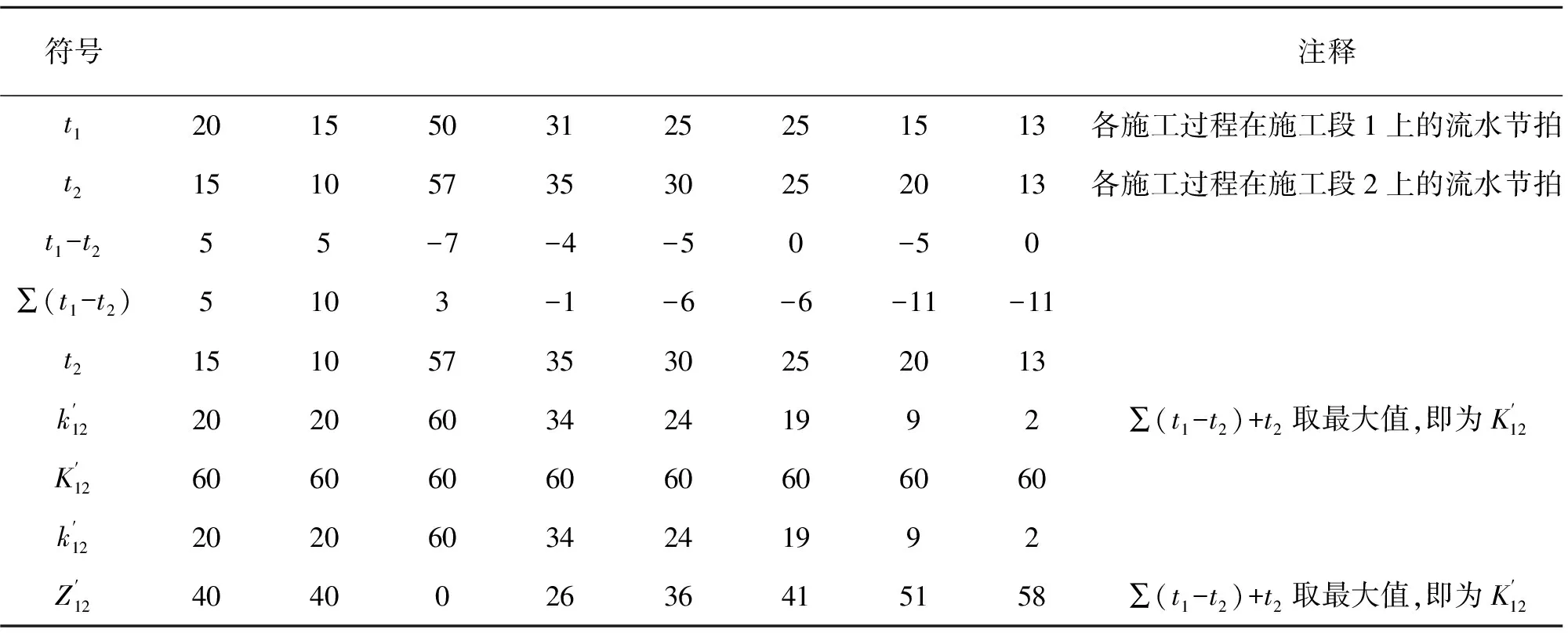
表6 施工段1和施工段2计算流程表

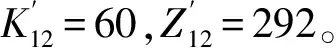
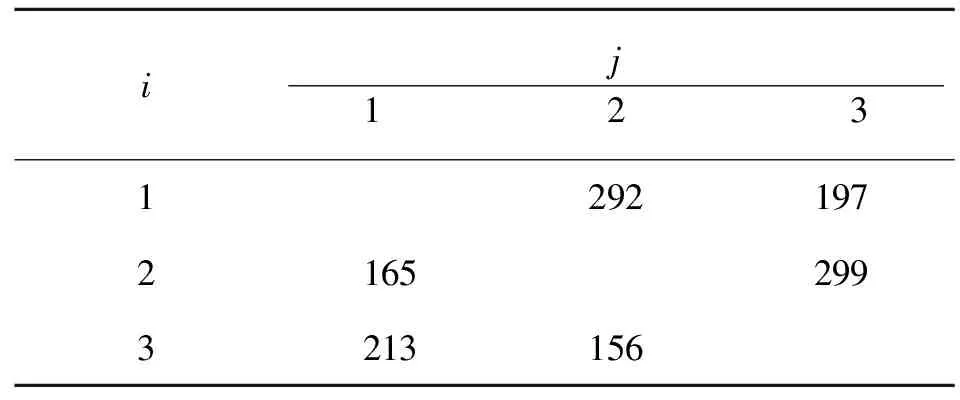
表7 排序间隙时间Zij矩阵表

根据矩阵法优化工期方法，可以确定最优施工段的顺序为2→1→3。

(5)依据优化后的施工段排序得表8。

表8 优化后的施工流水段上的流水节拍

(6)依次求出所有施工过程间的流水步距。

依据上述施工过程间的流水步距的计算过程，求出：K1=25，K2=10，K3=91，K4=46，K5=30，K6=35，K7=24。

(7)将所有数据带入工期的计算公式。

T′=∑Ki,i+1+tn+∑Z1+∑Z2+∑D=261+19=280(天)；

(8)通过比较，优化后的工期比初步计划的工期少了5天，绘制最终施工进度计划如图4所示。

图4 最终施工进度计划图

为了验证本文提出的基于矩阵法的无节奏流水施工优化技术在实际应用中的性能，采用传统的基于候鸟优化算法的无节奏流水施工优化技术和本文提出的基于矩阵法的无节奏流水施工优化技术，在保证无节奏流水施工质量的基础上，对无节奏流水施工时间进行对比分析，对比结果如图5所示。

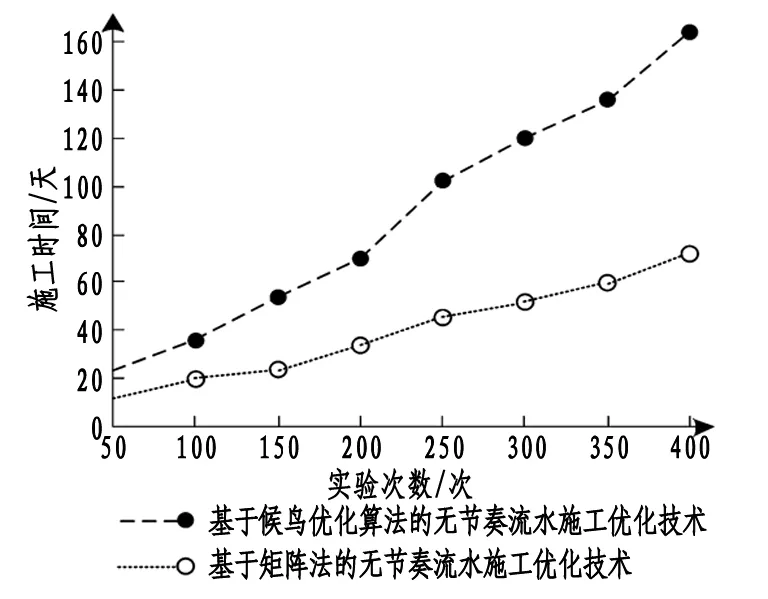
图5 无节奏流水施工时间对比结果

采用本方案提出的基于矩阵法的无节奏流水施工优化技术进行无节奏流水施工时间为80天，采用传统的基于候鸟优化算法的无节奏流水施工优化技术进行无节奏流水施工时间为160天，本文提出的基于矩阵法的无节奏流水施工优化技术的无节奏流水施工时间比传统的基于候鸟优化算法的无节奏流水施工优化技术的无节奏流水施工时间短，说明本文提出的基于矩阵法的无节奏流水施工优化技术能够缩短无节奏流水施工进度，提高施工效率。

3.3 结果分析

先后通过理论及案例对矩阵法优化无节奏流水工期进行探讨，过程中运用矩阵法对理论及案例中的施工段排序进行最优化，使得各施工过程的间隙时间和最小，计算结果显示经优化后的工期分别减少了1天、5天，说明矩阵法可以有效地减少工期时间。综上，可得出在各分项工程次序不能改变的情况下，可以利用该优化方法得到最优施工段顺序来达到减少施工工期的目的，同时达到缩减施工成本的效果。在不增加任何成本以及其他外界因素的情况下，该优化方法仍然可以使用，具有实际运用价值。方法适用于含有多个施工过程、施工段的施工项目，搭配Excel等工具可以快速地对最优施工段顺序进行快速求解。并通过与传统的无节奏流水施工优化技术进行仿真对比，验证本文方法的有效性，在保证无节奏流水施工质量的基础上，无节奏流水施工进度最短。

4 结论

本研究主要通过提出矩阵法优化无节奏流水工期的方案，从理论与实际两个方面依次进行验证，结果表明无论是从理论方面还是实际方面，该优化方案均起到了缩减工期、降低成本的效果。同时优化中的计算流程可利用计算机计算软件辅助计算，可在较短时间内求出多施工过程、多施工段施工项目的最优施工段顺序，在一定程度上也减少了人力、物力的耗费。并且实际施工中无节奏流水施工最为普遍，施工方每时每刻均会面临对工期和成本的控制问题，所以本优化方案具有较好的应用价值和前景。