考虑水泥-水玻璃双液浆黏度时空效应的隧道预注浆研究
2021-09-22查丽娟马智永
查丽娟,马智永
(1.河南建筑职业技术学院 工程管理系, 河南 郑州 450001;2.郑州大学 土木工程学院, 河南 郑州 450001)
近年来,随着我国城市轨道交通网络的不断完善及城市地铁工程的大规模建设,新建地铁线路穿越岩溶地层、断层破碎带及富水砂层等不良地质条件的情况逐年增多[1-3].其中地铁车站结构较为复杂且功能单元繁多,往往成为整条地铁线路能否顺利贯通的控制性工程.地铁车站在穿越不良地质时大多采用超前注浆的方式对周边地层进行预加固,以最大程度上保证暗挖施工的安全.
隧道超前注浆是先将具有充填胶结性能的浆液注入掌子面前方的地层中,以提高地层的强度和稳定性,降低其渗透性,形成较大范围的筒状封闭加固区,然后在其范围内进行洞室的开挖作业.目前,隧道工程中常采用的预注浆方法有:掌子面注浆、地表预注浆和平行导坑对正洞注浆三种方式[4].针对不同的被注介质性质、注浆参数和浆液特性,浆液的扩散可分为:充填、渗透、压密和劈裂四种形式[5].同时,根据浆液在外力作用下的流变性,又可以将浆液划分为牛顿流体、宾汉姆流体和幂律型流体三种流型[6].
目前,渗透注浆是应用最为广泛的一种注浆方法.关于渗透注浆技术在隧道超前注浆中的应用研究,国内外学者做了大量工作.陈治[7]等分别基于均匀管组理论和非均匀管组理论,推导了考虑牛顿流体黏度时变性时的球面和柱面渗透扩散半径计算公式.杨志全[8-11]等采用理论分析的方法,研究了黏度时变性宾汉姆和幂律型水泥浆液的球形、柱形和柱-半球形渗透注浆扩散机制,并通过室内注浆试验对其进行了验证.叶飞[12-13]等假定注浆浆液为黏度时变性流体,应用达西定律对盾构隧道壁后注浆浆液柱面和半球面渗透扩散半径及浆液对管片造成的注浆压力进行了理论推导,并就是否考虑黏度时效性两种条件下浆液扩散半径以及对管片产生压力的计算结果进行了对比分析.张连震[14]等运用流体两相渗流理论描述了动水条件下的渗透注浆扩散过程,并建立了相应的有限元模型对注浆过程进行数值模拟.张庆松[15]等设计了一套由注浆工艺模块、被注介质模块和信息采集模块构成的断层泥注浆加固试验系统,并开展了断层泥注浆加固体的相应特征试验.
从以上研究成果可以看出,针对水泥单液浆的渗透扩散机制研究已经从不考虑浆液的黏度时效性阶段发展到了考虑浆液的黏度时效性阶段,这些研究成果均促进了注浆技术的理论发展.目前,水泥-水玻璃双液浆作为典型的速凝型浆液在注浆工程中的应用日益增多,但是对于双液浆渗透扩散机理的研究较少.基于此,本文以青岛地铁四号线人民会堂站的地表超前注浆工程为研究背景,考虑水泥-水玻璃双液浆的黏度时效性和黏度空间效应,对双液浆的渗透注浆扩散机制进行理论研究,给出浆液扩散半径的计算公式,以期为水泥-水玻璃双液浆在隧道不良地质地段超前注浆中的应用提供理论依据.
1 C-S双液浆柱形渗透扩散模型
1.1 C-S双液浆的黏度时空效应
1.1.1 双液浆的流变方程
由于水泥单液浆凝固时间较长、浆液的扩散范围难以控制且易受到地下水的稀释[16],水泥-水玻璃(C-S)双液浆作为典型的速凝型浆液在注浆工程中得到了广泛的应用.C-S双液浆由水泥类浆液(A液)和水玻璃类浆液(B液)按一定的比例混合后得到,混合后的浆液既具有水泥强度高的特点,又具有化学浆液能准确控制凝固时间的优点.C-S双液浆黏度变化显著,从浆液混合至浆液失去流动性所需时间(凝胶时间)一般为几十秒至几十分钟.双液浆黏度变化可以分为三个阶段[17],即低黏期、上升期和固化期,其黏度阶段划分见图1.

图1 C-S双液浆的黏度阶段划分Fig.1 Viscosity stage division of C-S mixed grout
李术才[18]等通过对试验数据进行拟合分析得到,当水泥浆水灰比为1且双液体积比也为1时,C-S双液浆的黏度时变方程为
μ(t)=AtB=0.003 182t2.23
(1)
式中:A、B均为常数,可根据双液浆的黏度-时间曲线拟合得到.
C-S双液浆为黏度时变性宾汉姆流体[18],其流变方程为
τ(t)=τ0(t)+μ(t)γ
(2)
式中:τ(t)为浆液的剪切应力;τ0(t)为浆液的屈服剪切力,用来表征浆液的塑性性质,根据阮文军[6]的研究成果可知:宾汉姆流体的屈服剪切力随时间变化可以忽略,因此有:τ0(t)=τ0(0)=τ0;μ(t)为浆液的黏度时变函数;γ为浆液剪切速率,γ=-dv/dr.
1.1.2 单液浆与双液浆注入方式的区别
水泥单液浆在使用时需事先按照水灰比配置好注浆浆液,然后由注浆泵注入到地层中,浆液注入地层后,浆液黏度随着时间的增加而不断增加.由于浆液的黏度起始时刻相同,因此注入地层中的浆液质点均经历了相同的黏度变化时间,各浆液质点的黏度值相同.
C-S双液浆在使用时是采用双重注入器,使两种浆液在注浆管口处混合,然后注入地层中,注入地层中的浆液质点其黏度随着时间的增加而迅速增加[19].浆液黏度起始时刻的不同导致浆液质点的黏度存在空间差异性[20],即先注入地层中的浆液质点其黏度值始终大于后注入地层中的浆液质点的黏度值.假设双液注浆的起始时刻为0,注浆的总时间为T.注浆起始时刻注入地层中的浆液质点扩散至半径l1处,质点的黏度增长时间为T;t时刻注入地层中的浆液质点扩散至半径l处,质点的黏度增长时间为T-t;T时刻注入地层中的浆液质点扩散半径为0,质点的黏度增长时间也为0.浆液扩散过程如图2所示.
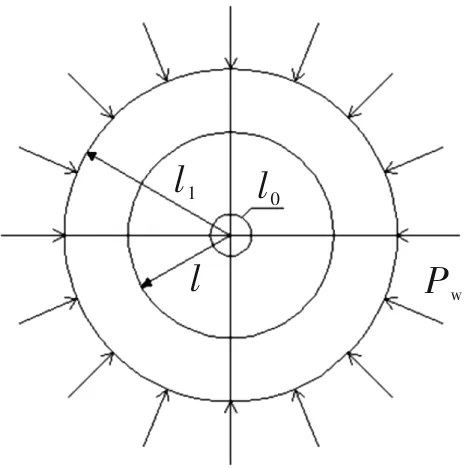
图2 C-S双液浆扩散过程示意图Fig.2 Diagram of diffusion process of C-S mixed grout
1.2 基本假设与计算模型
针对本文所研究的问题,提出以下基本假定:
(1)浆液为均质、各向同性及不可压缩的流体,且不考虑浆液重力的影响;整个注浆过程中浆液的流型保持不变.
(2)浆液流速较小,浆液仅在注浆孔周围局部区域呈紊流状态,其余部分皆为层流状态.
(3)受注地层为均质、各向同性介质.
(4)注浆管内浆液的流速不变,浆液以渗透扩散的形式进入地层.
(5)C-S双液浆为黏度时变性的宾汉姆流体,其流变方程为式(2).
(6)浆液扩散锋面在静水压力作用下不发生稀释现象,即浆液与地下水的相界面是突变的[21].
当采用袖阀管后退式分段注浆工艺时,浆液在被注介质中呈柱形扩散[10].浆液柱形扩散的理论模型见图3.
1.3 公式推导
1.3.1 双液浆黏度变化时间与扩散半径的关系
根据T时间内浆液在地层中渗透扩散的量与注浆管注浆量相等,可得到:
(3)
则注浆总时间为:
(4)
式中:l0为注浆管半径;v0为注浆管内浆液的流速;q为注浆管的流量;m为浆液柱形扩散的高度;φ为受注地层的孔隙度.
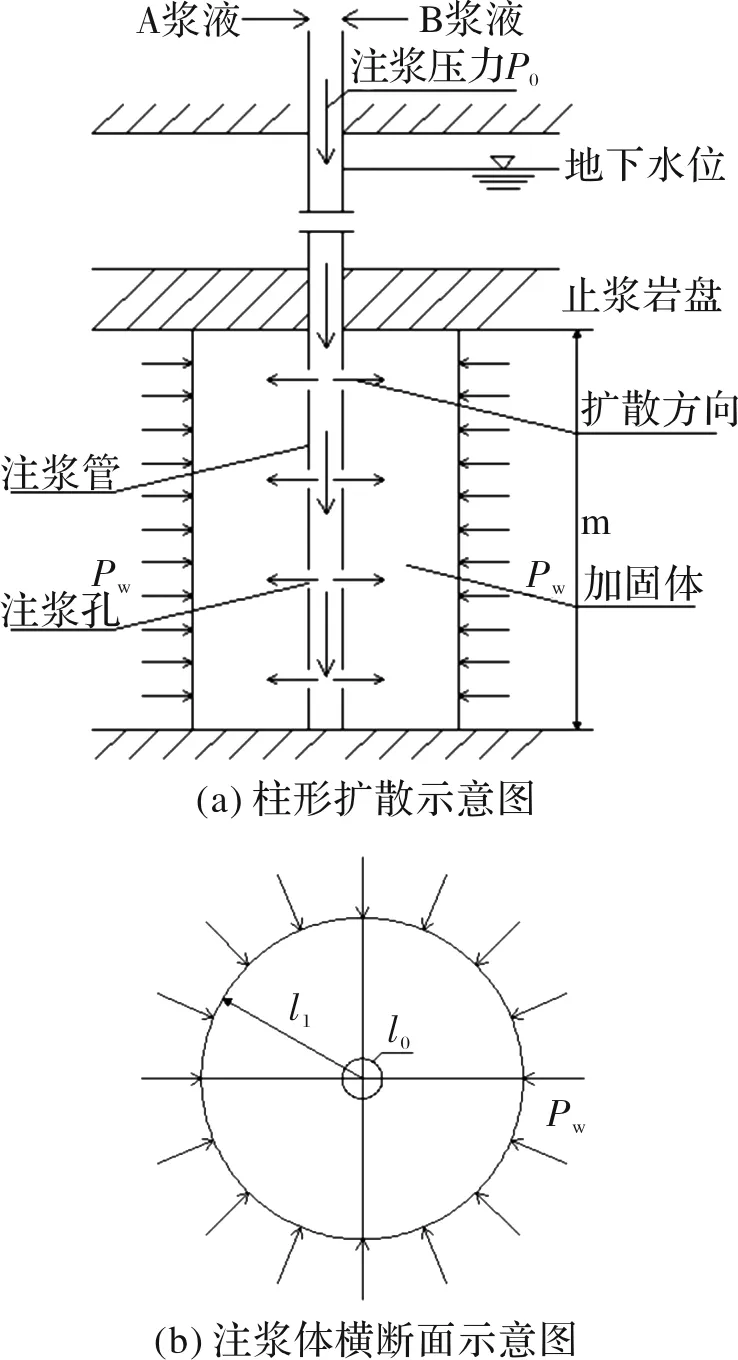
图3 浆液柱形扩散理论模型Fig.3 Theoretical model of grout cylindrical diffusion
由1.1.2节可知:t(t≤T)时刻注入地层中的浆液质点,其最终扩散至半径l处.令Tu=T-t,则从t时刻至注浆结束时刻,即Tu时间段内,注入地层中的浆液量为
(5)
则有
(6)
由于注浆管内浆液的速率不变,因此对地层中某一确定的浆液扩散半径l,浆液质点由注浆孔处到达该位置所需要的时间是固定不变的,而浆液质点由注浆孔处到达该位置所需要的时间也就是浆液的黏度增长时间Tu,即对扩散半径l处的浆液质点而言,其黏度增长时间是固定不变的[22].由此可知:浆液质点的黏度增长时间与浆液的扩散半径l一一对应,即Tu=T(l),所以有
(7)
1.3.2 双液浆的渗流运动方程
假定受注地层为由直径相同的毛细管排列而成的多孔介质,即符合均匀毛管组模型,双液浆的渗流等效为浆液质点在所有毛细管道中流动的叠加[23].设毛细管半径为r0,在毛细管中取一段与管轴同轴的流体柱微元素,流体柱半径为r(r≤r0),长度为dl,流体柱的左右两端分别作用压力P和P+dP,两侧的压力差为dP,流体柱的表面上所受剪切应力为τ,其方向向左,与浆液的流动方向相反,浆液在毛细管道中的流动情况如图4所示.
由流体柱微元素的受力平衡条件可得到:
Pπr2-πr2(P+dP)-2πrτdl=0
(8)
化简得到浆液的剪切应力为
(9)

图4 浆液在毛细管道中的流动示意图Fig.4 Flow diagram of grout in capillary pipe
当剪切应力τ≤τ0时,浆液不发生相对运动,呈活塞式运动;当剪切应力τ>τ0时,浆液发生相对运动.结合图4可知,毛细管中浆液的速度分布为截头抛物面形状.令τ=τ0,可得到浆液活塞式运动的半径为
(10)
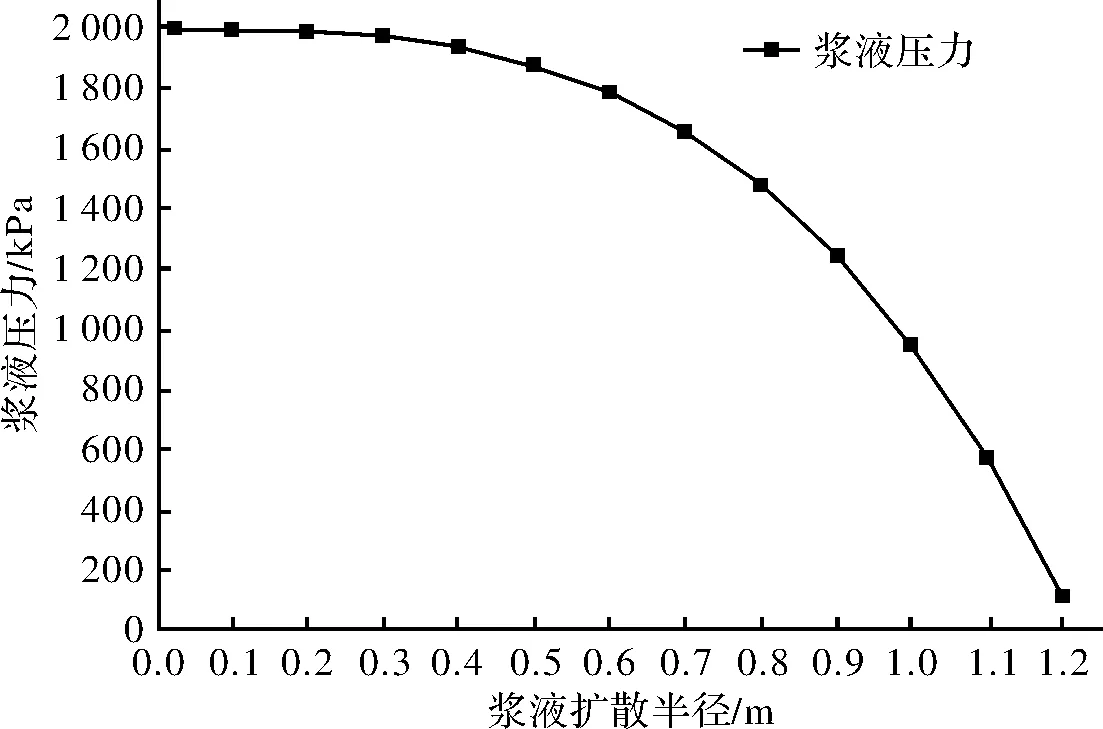
由此可以说明当0≤r≤rp时,浆液的剪切应力τ为0,当rp 图5 浆液剪应力分布示意图Fig.5 Diagram of shear stress distribution in grout 将式(9)代入双液浆的流变方程式(2),可得到: (11) 对式(11)采用分离变量法积分,代入壁面无滑移条件r=r0,v=0,可得到浆液的速度方程为 (12) 所以有 (13) 毛细管道中浆液的总流量Q为活塞运动区与相对运动区两部分的流量之和,即 (14) 则浆液在毛细管中的平均流速为 (15) 浆液需要克服阻碍其流动的屈服剪切力τ0,即达到浆液的启动压力梯度λ,才能保证浆液能在毛细管中顺利流动.令Q=0,可解得: (16) (17) 被注介质渗透率K与毛细管半径r0满足如下关系: (18) 由于注浆开始后其压力梯度-dP/dl?启动压力梯度λ,忽略高阶微量并结合式(17)可得到: (19) (20) 采用分离变量法对式(20)进行积分可得到: (21) 式中:C为积分常数. 代入注浆边界条件: (22) 式中:P0为注浆孔处的注浆压力;Pw为注浆点处的地下水压力. 令ΔP=P0-Pw,由式(21)和(22)可得到: (23) 由此可得浆液的扩散半径表达式为 (24) 根据浆液扩散半径l处的浆液压力为P,同时结合注浆边界条件,对式(20)进行积分,得 (25) 可得到浆液压力的表达式为 (26) 1.4.1 参数确定方法 由以上公式推导的过程可以看出,与双液浆柱形渗透扩散过程相关的参数有:初始扩散半径l0,双液浆的屈服剪切力τ0,注浆点处的地下水压力Pw,注浆压力P0,毛细管半径r0,双液浆黏度参数A和B,受注地层孔隙度φ,浆液柱形扩散的高度m,受注地层渗透率φ,注浆管内浆液的流速v0. l0为注浆管半径,可以通过多次测量求平均值获得;屈服剪切力τ0采用旋转黏度计或毛细管黏度计测定得到;地下水压力Pw由公式Pw=ρgh计算得到(ρ为水的密度,h为注浆段的埋深);注浆压力P0采用在注浆孔附近安装压力表,由现场测试数据得到;渗透率K由公式K′=Kρg/μw计算得到[24](K′为渗透系数,μw为水的黏度);孔隙度φ可在室内或现场测定得到;在已知K和φ的前提下可由式(18)计算出毛细管半径r0;黏度参数A和B可由室内浆液特性试验得出相关数据后拟合得到;柱形扩散的高度m可根据工程设计要求获得;浆液的流速v0可由现场实测得到. 至此,对于考虑黏度时空效应时C-S双液浆柱形渗透注浆的扩散半径计算式(24),除了浆液扩散半径l1一个未知参数外,其他参数均可通过上述方法得到;反之,已知浆液扩散半径l1,可以由式(23)求出理论上的压力差ΔP.在求得浆液扩散半径l1后,由式(26)可以得出浆液扩散范围内浆液压力的衰减规律. 1.4.2 公式适用范围 以上公式均是在假定浆液流态为层流的情况下推导出来的,当浆液流态为紊流时,上述公式不再适用.张伟[25-26]等的研究表明:当雷诺数Re<2 000时浆液为层流流态,当2 000≤Re≤4 000时浆液为层流与紊流的混合流态,当4 000 雷诺数的计算式为 (27) 青岛地铁四号线人民会堂站为地下两层11m岛式车站,采用矿山法施工,有效站台中心里程为ZDK0+372.500.车站主体范围内存在两处断层、一处节理.F1断裂为青岛山断裂的次生断裂,F2断裂为青岛山断裂.车站上覆围岩松散破碎,自稳能力较差.场区地下水主要类型为第四系孔隙潜水与基岩裂隙水,由于车站毗邻黄海,场区内水源补给较为充足.车站平面位置图如图6,现场钻孔取芯情况如图7. 图6 人民会堂站平面位置图Fig.6 Plane location map of People’s Hall Station 图7 现场钻孔取芯情况Fig.7 On-site drilling core feeding condition 在车站主体结构施工前采用地表+洞内的联合钻孔方案对开挖断面周边进行注浆加固,地表注浆孔横断面布置见图8.地表采用模袋袖阀管注浆工艺加固隧道开挖面正上方的影响区域,该工艺首先在目标加固区域上方构造止浆岩盘,止浆岩盘形成以后再将双液浆注入地层中,从而保证了双液浆始终在目标加固区域内渗透扩散,防止浆液沿着岩层裂隙渗透到海水中以及沿着注浆管壁上窜,造成材料浪费和环境污染;洞内采用常规注浆工艺加固隧道拱顶侧边部位和边墙及底板的外侧区域.地表注浆加固区域的宽度为15 m,高度为6 m(为保证注浆加固效果,钻孔延伸到隧道轮廓线内1 m);隧道拱顶侧边部位的加固圈厚度为5 m,注浆孔终孔间距为2.5 m,其他部分的加固圈厚度为3 m,注浆孔终孔间距为4 m,注浆分段长度为4~5 m. 图8 地表注浆孔横断面布置图(单位:m)Fig.8 Cross section layout of grouting holes on the surface(Unit: m) 由工程设计资料可知:注浆点处的地下水压力Pw=115 kPa,浆液流速v0=2.4 m/s,双液浆黏度参数A=0.003182,黏度参数B=2.23(水泥浆水灰比为1且双液体积比也为1),同时选定初始扩散半径l1=0.025 m,屈服剪切力τ0=1.563 Pa,注浆压力P0=2 MPa,受注地层孔隙度φ=0.3,浆液柱形扩散的高度m=6 m,渗透系数K′=0.12 cm/s,20℃时水的黏度μw=1.005×10-3Pa·s. 在双液浆注入过程中,如果注浆压力太小,则无法将浆液快速的注入到地层中,从而无法对目标加固区域的土体进行有效加固;如果注浆压力太大,则双液浆在地层中的作用方式可能由渗透扩散演变为压密扩散,甚至发生劈裂扩散,造成浆液流失,从而达不到预期的加固目的.因此,在获得较大的浆液加固半径的同时又要考虑注浆过程中被加固土体的稳定性,防止其发生过大变形而劈裂破坏.利用1.3.2节中的公式(24),并结合本节中的基本参数,计算不同注浆压力P0下浆液扩散半径l1的值,根据计算结果作出曲线如图9所示. 由图9可知,随着注浆压力P0的不断增大,双液浆扩散半径l1亦随之增大.相应曲线大致呈现三阶段变化:即当注浆压力P0从0.2 MPa增加至0.8 MPa时,浆液扩散半径快速增加;当注浆压力P0从0.8 Pa增加至2.0 Pa时,浆液扩散半径的增加速率逐渐减小;当注浆压力P0从2.0 MPa增加至2.8 MPa时,浆液扩散半径缓慢增加. 一般而言,为了获得较好的注浆加固效果,往往需要较大的浆液扩散半径并且对地层的影响较小,由图9可知,较理想的注浆压力为2.0 MPa,此时浆液得以充分扩散,浆液扩散半径为1.2 m. 图9 注浆压力对浆液扩散半径的影响规律Fig.9 The influence of the grouting pressure on grouting diffusion radius 选定注浆压力P0=2.0 MPa,利用2.3.2节中的公式(26),并结合本节中的基本参数,计算浆液扩散半径范围内不同位置处所对应的浆液压力值,根据计算结果作出曲线如图10所示. 图10 浆液压力随浆液扩散半径增大时的衰减规律Fig.10 Attenuation rule of grout pressure with increasing grouting diffusion radius 由图10可知,随着浆液扩散半径的增加,浆液压力逐渐减小.当浆液扩散半径从0.025 m增加至0.3 m时,浆液压力缓慢减小;当浆液扩散半径从0.3 m增加至0.8 m时,浆液压力加速减小;当浆液扩散半径从0.8 m增加至1.2 m时,浆液压力快速减小,且最终值等于注浆点处的地下水压力115 kPa.由此可见,在注浆压力一定的条件下,浆液扩散半径逐渐增大至接近最终的扩散半径时,地下水对浆液渗透扩散的阻碍作用愈加明显,并最终导致浆液压力呈现出快速衰减的趋势. 地表注浆施工完成后,对注浆加固区域进行了取芯检验,钻孔取芯情况如图11所示.检验结果表明:注浆范围内的岩芯以水泥结石体为主,岩体完整性得到大幅提高;现场开挖过程中,未造成地表沉降超限和洞内垮塌事故,满足安全开挖的要求. 图11 钻孔取芯结果Fig.11 Drilling core results (1)水泥-水玻璃双液浆为黏度时变性的宾汉姆流体,基于双液浆的流变方程,同时考虑双液浆的黏度时效性和黏度空间效应,推导得到了表征双液浆黏度增长时间Tu与浆液扩散半径l之间关系的表达式. (2)根据此关系式并结合均匀毛管组理论,推导得到了考虑双液浆黏度时空效应的柱形渗透注浆浆液扩散半径l1和浆液压力P的理论计算公式,并分析了公式中相关参数的确定方法与公式的适用范围. (3)将本文所得的浆液扩散半径理论计算公式应用于人民会堂站的模袋袖阀管注浆工程中,由浆液扩散半径l1随注浆压力P0的变化规律可以得出:当注浆加固效果最佳时,注浆压力P0=2.0 MPa,此时浆液扩散半径l1=1.2 m. (4)本文所推导的理论计算公式丰富和发展了注浆理论体系,对类似工程的预注浆设计、施工提供了良好的借鉴和参考价值.
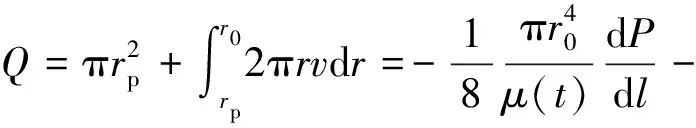
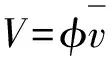
1.4 参数确定方法与公式适用范围

2 工程实例应用
2.1 工程概况



2.2 双液浆扩散半径的确定

2.3 注浆效果检验

3 结论
