高强钢筋与超高性能混凝土黏结性能试验研究
2021-09-22胡翱翔梁兴文史庆轩陈宜言陈宝春李睿璞
胡翱翔,梁兴文,史庆轩,陈宜言,陈宝春,王 群,李睿璞
(1.深圳职业技术学院 建筑与环境工程学院,广东 深圳 518055;2.西安建筑科技大学 土木工程学院,陕西 西安 710055; 3.福州大学 土木工程学院,福建 福州 350108)
近年来,随着科学技术的进步,土木工程材料领域有了很大的革新,出现了超高性能混凝土(Ultra-High Performance Concrete,简称UHPC)等新型土木工程材料.UHPC与普通混凝土相比其抗压、抗拉以及抗剪等力学性能均大幅提升[1],钢纤维的加入,可以明显改善混凝土的脆性,同时起到阻裂的作用,UHPC与普通混凝土的力学性能相差较大.研究表明[2-3]:钢筋与混凝土的黏结性能与混凝土材料的力学性能密切相关,故现有的规范不再适用于这种新材料.近年来随着建筑结构向着大跨、高层、高耐久性、高性能[4]等方向发展,UHPC材料在国内外工程中已经有所应用[1-5],为了UHPC材料在工程结构中的推广应用,有必要研究钢筋与UHPC之间的黏结性能,建立钢筋与UHPC材料的黏结应力-滑移本构方程.
国内外研究人员对钢筋与UHPC材料的黏结性能进行了一些研究.M.Harajli[2]等通过梁式试验研究了钢筋与纤维混凝土以及普通混凝土黏结性能的差异,试验考虑的变量有保护层厚度和纤维掺量.试验结果表明:与普通混凝土相比,纤维的加入显著增大了试件发生破坏时的劈裂强度以及延性;随着保护层厚度的增加,黏结强度增加.Doo-Yeol Yoo[6]等通过中心拔出试验,研究纤维掺量分别为1%、2%、3%和4%时对钢筋与UHPC黏结性能的影响.试验结果表明:纤维掺量小于3%时,极限黏结强度及其对应的滑移值随着纤维掺量的增加而增加;继续增加纤维掺量,极限黏结强度反而降低.Baek-Il Bae[7]等通过中心拔出试验,研究活性粉末混凝土(以下简称RPC)强度、保护层厚度和钢纤维掺量对钢筋与RPC黏结性能的影响.试验结果表明:钢纤维掺量从0%增加至1%时,极限黏结强度增加了一倍,但是继续增加至2%时,极限黏结强度仅增加2%~5%;黏结强度与RPC强度以及保护层厚度成正比.文中通过计算发现发生劈裂破坏试件的黏结强度可以用Tepfers[8]提出的计算模型进行计算.F.Baby[9]等研究法国市场上常见的HRB500钢筋与UHPC的黏结性能.试验结果表明:黏结强度随着钢筋直径(12 mm和16 mm)增加而增加,此结果与普通混凝土研究结果相反;保护层厚度和黏结长度对黏结性能影响趋势与普通混凝土相同;循环加载和静力加载两种加载方式对试验结果的影响可以忽略不计.
贾方方[10]为研究HRB335变形钢筋与高温养护RPC的黏结性能,进行了13组梁式试验和5组中心拔出试验.试验结果表明:试件的黏结破坏形式与纤维掺量、保护层厚度和粘结长度均相关;随着纤维掺量的增加,试件的破坏形态从混凝土劈裂破坏变化为劈裂破坏和钢筋拔出共同发生,最后变为仅钢筋拔出的粘结破坏形式;黏结强度及其相应的滑移值与钢纤维体积掺量成正比;随着保护层厚度的增加,黏结强度增加,峰值滑移基本不变;随着粘结长度的增加,粘结强度和峰值滑移均减小.文中根据试验数据进行统计分析建立了黏结强度计算公式,并建立了劈裂黏结破坏强度理论计算公式.邓宗才[11]等通过72个拉拔试件研究了HRB500级高强钢筋与RPC的黏结性能.试验结果表明:随着钢纤维体积掺量的增加,黏结-滑移曲线下降段变缓;纤维掺量较小时,对试件的破坏形式、黏结强度影响不大;黏结强度与保护层厚度和RPC强度成正比,与钢筋直径和粘结长度成反比.安明喆[12-13]等分别对Q235光圆钢筋和HRB335变形钢筋与RPC黏结性能的影响.试验结果表明:随着钢筋直径的增加,相对黏结面积减小,黏结强度减小;随着粘结长度的增加,黏结强度减小.
由上述国内外研究分析可知:钢筋与UHPC材料的黏结性能与普通混凝土显著不同;钢筋直径对黏结性能的影响存在争议;目前国内工程中一般采用HRB400级钢筋,对HRB500、HRB600等高强钢筋的应用相对较少,高强钢筋的大规模推广应用是未来的发展趋势之一.基于此,本文设计了15组常温养护条件下的立方体中心拔出试件,研究钢筋直径、锚固长度以及保护层厚度三个因素对钢筋与UHPC黏结性能的影响,并建立黏结强度计算公式及黏结应力-滑移本构方程.
1 试验概况
1.1 试验材料
试验所用UHPC材料的配合比详见文献[14].试验所用钢纤维为表面镀黄铜的圆柱形短纤维,长度为7 mm,等效长径比为39,抗拉强度大于2 850 MPa.各组试件钢纤维体积掺量均为3%,一共15组试件.试件制作完成之后表面用湿布覆盖,放置室外养护48 h后拆模,试件制作完成后的前14 d,每天早、晚浇水养护两次,之后每天浇水养护一次至28 d龄期,之后继续放在室外直至试验.与试件同条件养护2组6个100 mm×100 mm×100 mm立方体试块,其28 d及试验当天龄期(165 d,试验过程中UHPC强度变化可忽略不计)的立方体抗压强度平均值分别为129.99 MPa和159.77 MPa.试验所用钢筋为HRB400 、HRB500和HRB600筋,钢筋实测物理、力学参数如表1所示.
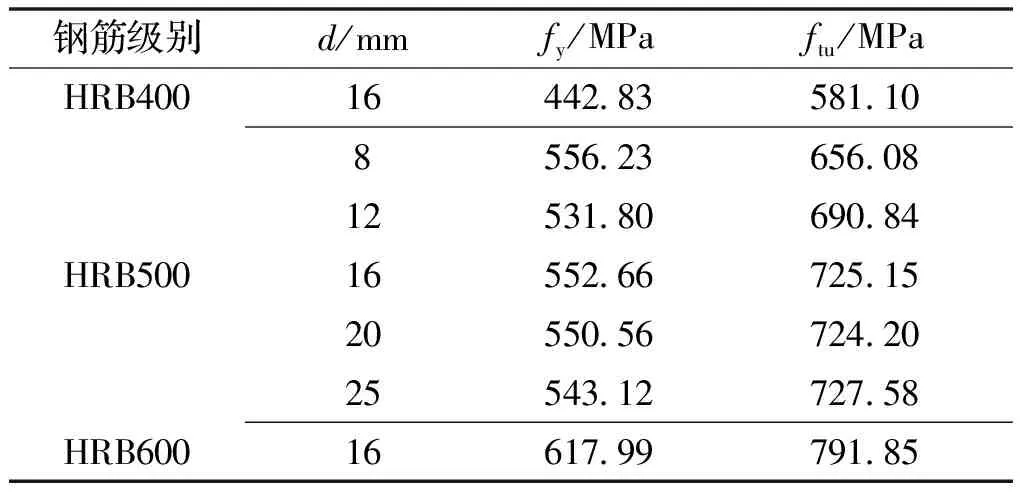
表1 钢筋力学性能指标
1.2 试件设计
试件尺寸参考CECS 13∶89《钢纤维混凝土试验方法》[15]中关于钢筋与混凝土黏结性能中心拔出试验的规定,确定为150 mm×150 mm×150 mm的立方体试件,钢筋与UHPC的黏结长度为l,钢筋距离加载端和自由端的非黏结区域lun范围内,先用透明胶带缠绕,之后在钢筋表面用PVC管套住,使其与周围混凝土隔离,防止振捣时,混凝土渗入非黏结区域而影响试验结果,同时防止试件加载端混凝土局部受压的影响.试件的具体尺寸如图1所示.

图1 试件设计图(单位:mm)Fig.1 Design of the specimen(unit: mm)
1.3 试验方案设计
此次试验一共制作15组试件,每组3个试件,考查钢筋直径、锚固长度、保护层厚度以及钢筋等级四个因素对变形钢筋与UHPC黏结性能的影响,其具体试验方案如表2所示.

表2 试验设计
1.4 试验加载过程
拔出试验在1 000 kN电子万能试验机上进行,试验时在钢筋自由端架设2个位移计,测量钢筋自由端与混凝土的相对滑移,荷载信号由机器自动采集.试验加载分为预加载和正式加载两个阶段,全过程采用位移控制.预加载阶段加载速率为5 mm/min,当荷载达到3 kN时进入正式试验,加载速率为0.5 mm/min,试件承载力下降到峰值荷载的35%或者位移计记录到的滑移值超过20 mm时,加载过程结束.试件的加载装置如图2所示.

图2 试验加载装置Fig.2 Test setup for the pull-out test
2 试验结果
2.1 试件破坏过程以及破坏形态
试验加载初期荷载增长较快,位移计读数基本为零,荷载增加至峰值荷载的80%左右时,位移计示数才开始缓慢增加,并一直持续至峰值荷载左右.峰值荷载过后位移计的示数增长速率明显加快,与此同时钢筋缓慢地从混凝土中被拔出.由于纤维的桥接作用,峰值过后试件承载力并没有迅速下降,荷载下降速率缓慢,滑移增加较快,伴随着纤维从基体中拔出的“哧哧”声.
此次试验试件的破坏形态共有两种:混凝土劈裂和钢筋被拔出共同发生的黏结破坏形式以及仅仅钢筋被拔出的黏结破坏形式.发生第一种破坏形式的试件是第4、5、9和10组,加载结束后试件的破坏形态如图3所示;其余组试件均为第二种破坏形式.








图3 劈裂+拔出破坏试件Fig.3 Splitting and pullout bond failure mode of the test
第4和第5组试件钢筋直径分别为20 mm和25 mm,钢筋表面的横肋尺寸比小直径钢筋更大,横肋楔形作用引起的挤压力更明显,所以钢筋在拔出的过程中受到阻力更大,当挤压力的径向分量引起的混凝土拉应力超过其抗拉强度时试件内部将会出现裂缝,继续增加荷载,当混凝土保护层厚度不足的时,裂缝将迅速延伸至试件表面.
第9和第10组试件钢筋的保护层厚度分别为1.0d和1.5d,钢筋直径为16 mm,保护层厚度较薄,同样是横肋的挤压作用的径向分量引起混凝土保护层较薄的一侧首先开裂;并且随着保护层厚度的增加,劈裂裂缝的数量减少、裂缝沿加载方向延伸的长度减小.
2.2 试验结果
本次试验所有试件钢筋的黏结长度相对较短(2d~3.5d),所以假定在钢筋黏结长度范围内钢筋与混凝土的黏结应力均匀分布,均等于平均黏结应力,计算公式为式(1).钢筋与混凝土的相对滑移取自由端两个位移计的平均值,计算公式为式(2).
(1)
(2)
式中:τ、τm分别表示黏结应力和平均黏结应力;F为拔出力;d为钢筋直径;l为黏结长度;s表示钢筋与混凝土的相对滑移;sf1、sf2分别表示钢筋自由端两个位移计的测量值.
本次试验各组试验的平均粘结强度、峰值荷载对应的平均滑移、加载过程中钢筋的平均最大应力以及试件最终的破坏形式列于表3.

表3 试验结果
2.3 平均黏结应力-滑移曲线
图4所示为15组试件的平均黏结应力-滑移曲线.由图可知:所有组试件的平均黏结应力-滑移曲线的走势大致相同,在达到峰值荷载之前,荷载大幅度增加但是滑移值却很小;峰值荷载过后,荷载开始下降,滑移值增长较快;当滑移值达到拐点时,荷载下降缓慢,并且有几组试件的承载力出现了二次上升的现象,这与邓宗才[11]等人观测到的试验结果一致.
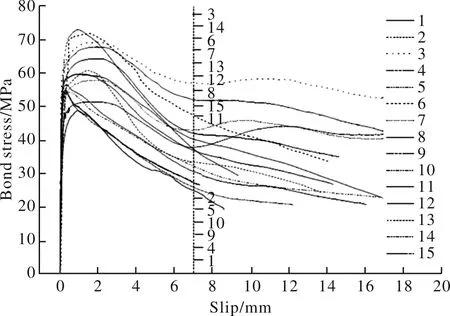
图4 平均黏结应力-滑移曲线Fig.4 Average bond stress-slip curves of all groups
钢筋从混凝土中逐渐拔出的过程中,由于钢筋与混凝土的摩擦作用以及纤维的拔出等过程均会耗散一定的能量,有利于结构在地震作用下耗散能量.试件在拔出过程中所耗散的能量可用黏结应力-滑移曲线与坐标横轴围成的面积表示,也称为拔出功[16].表4列出了各组试件平均黏结应力-滑移曲线峰值点之前以及下降段拐点之前曲线与坐标横轴所围成的面积.

表4 平均黏结应力-滑移曲线与坐标横轴围成的面积
3 试验结果分析
3.1 钢筋直径对黏结性能的影响
图5所示为钢筋直径对黏结强度以及峰值滑移的影响曲线.由图可知:当钢筋直径≤16 mm时,试件均发生拔出黏结破坏,黏结强度和峰值滑移均随钢筋直径的增加而增加,即钢筋直径从8 mm增加至16 mm时,黏结强度从48.81 MPa增加至69.23 MPa,增长率为42%;峰值滑移从0.93mm增加至1.56 mm,增长率为68%.继续增加钢筋直径,试件发生劈裂加拔出的黏结破坏,黏结强度和峰值滑移均降低,可能是由于粗钢筋表面横肋尺寸更大,钢筋拔出过程中横肋对周围混凝土的挤压作用更大,当挤压力的径向分量超过混凝土的抗拉强度时,混凝土内部会出现裂缝,当混凝土保护层厚度不足时,裂缝将延伸至试件表面,试件开裂之后,混凝土对钢筋拔出过程的抵抗力减弱,所以承载力将降低.并且同样发生劈裂加拔出黏结破坏的试件(直径为20 mm和25 mm),其黏结强度和峰值滑移也是随着钢筋直径增大而增大.这个试验结果与国内外的研究人员的试验结果不同[11,13,17-18],但与Marchand.Pierre[9]等人的试验结果相似.作者分析可能是由于此次试验所用钢纤维与其他研究人员相比长度更短、直径更大,纤维数量更多,在振捣混凝土的过程中短纤维更容易下沉至试件下部区域,纤维分散更均匀;钢筋拔出的过程中受到钢筋横肋间钢纤维的抵抗作用更明显;即随着钢筋直径的增大,钢筋的横肋高度增加,横肋间钢纤维对钢筋拔出的阻挡作用增大的幅度超过由于钢筋相对黏结面积减小导致黏结强度降低的幅度.

(a)直径对黏结强度的影响
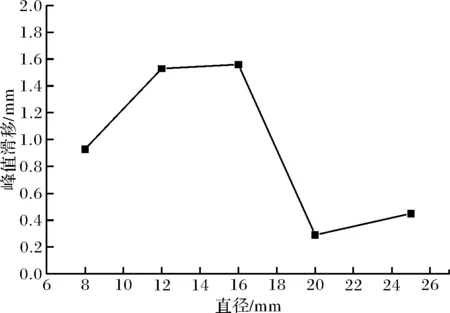
(b)直径对峰值滑移的影响图5 钢筋直径对黏结强度和峰值滑移的影响Fig.5 Effect of bar diameter on bond strength and corresponding slip
图6所示为钢筋直径对钢筋与混凝土平均黏结应力-滑移曲线的影响分析.由图可知:钢筋直径≤16 mm时,试件均发生拔出黏结破坏,随着钢筋直径增大,曲线越来越饱满,下降段也越来越平缓,钢筋拔出过程中耗散的能量越来越多,并且直径为16 mm时下降段曲线出现二次上升的现象.当钢筋直径为20 mm和25 mm时,峰值过后试件发生劈裂,荷载先是迅速下降,如图6(b)所示,随后由于纤维的桥连作用试件的承载力下降速度减慢.由于试件发生劈裂,下降段曲线不饱满,钢筋拔出过程中耗散的能量较少.这也可从表4中看出,五组试件滑移值达到拐点滑移值之前的平均黏结应力-滑移曲线与坐标横轴围成的面积比例为:0.57∶0.74∶1.00∶0.60∶0.66.

(a)黏结应力-滑移曲线上升段

(b)完整的黏结应力-滑移曲线图6 钢筋直径对平均黏结应力-滑移曲线的影响Fig.6 Effect of bar diameter on average bond stress-slip curves
3.2 钢筋黏结长度对黏结性能的影响
图7所示为钢筋黏结长度对黏结强度和峰值滑移的影响分析.由图可知:黏结强度随着黏结长度的增加而减小,即:黏结长度从2d增加至3.5d时,黏结强度从71.79 MPa减小至51.45 MPa,下降率为28%.峰值滑移随着黏结长度的增加而增加,即:黏结长度从2d增加至3.5d时,峰值滑移从1.49 mm增加至1.88 mm,增加率为26%.这个结论与普通混凝土相似.
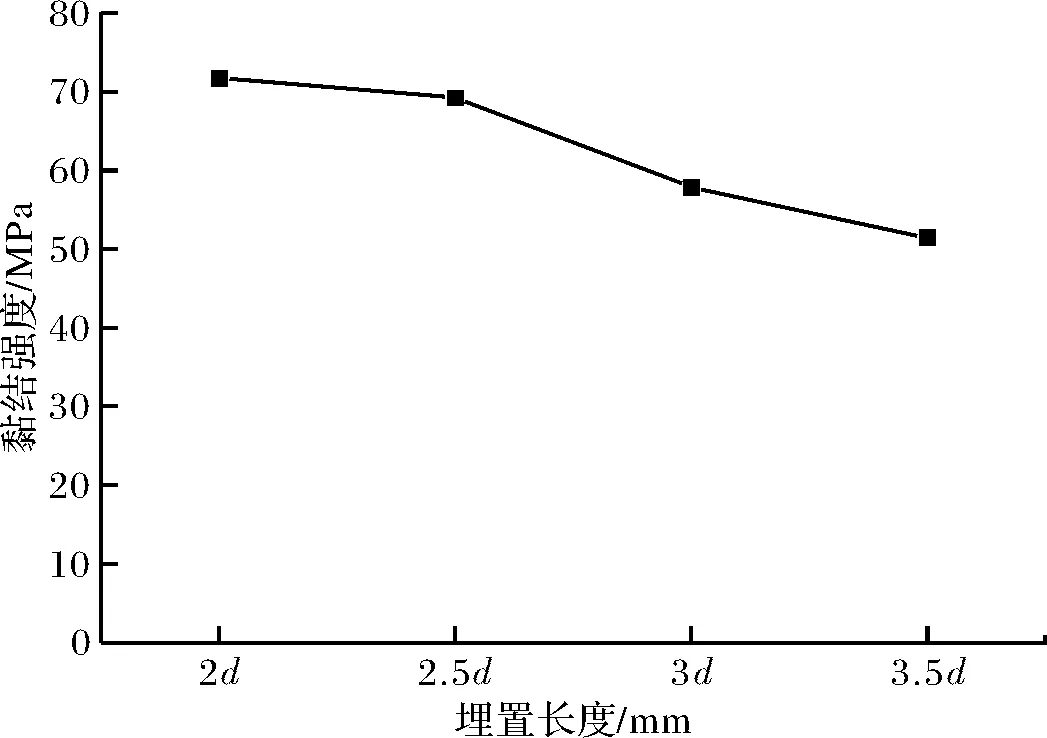
(a)埋置长度对黏结强度的影响

(b)埋置长度对峰值滑移的影响图7 钢筋黏结长度对黏结强度、峰值滑移的影响Fig.7 Effect of embedment length on bond strength and corresponding slip
钢筋黏结长度对平均黏结应力-滑移曲线的影响如图8所示.由图可知:曲线的趋势基本相同,所有组的下降段曲线都比较饱满,且均出现荷载二次上升的现象,表明钢筋拔出过程中试件的耗能能力较强.随着黏结长度的增加,曲线与坐标横轴之间围成的面积逐渐减小.由表4可知:黏结长度从2d增加至3.5d时,拐点之前平均黏结应力-滑移曲线下围成的面积比例为:0.94∶1.00∶0.80∶0.72.

(a)上升段曲线
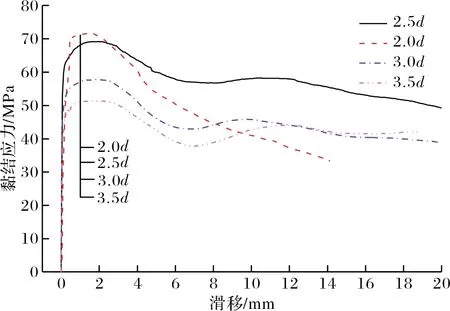
(b)完整曲线图8 黏结长度对平均黏结应力-滑移曲线的影响Fig.8 Effect of embedment length on average bond stress-slip curves
3.3 保护层厚度对黏结性能的影响
图9所示为钢筋保护层厚度对平均黏结强度、峰值滑移的影响分析.由图可知:随着保护层厚度的增加,黏结强度和峰值滑移均不断上升,即保护层厚度从1d增加至3d时,黏结强度从55.31 MPa增加至64.33 MPa,峰值滑移从0.24 mm增加至1.74 mm.黏结强度和峰值滑移的增长率分别为16%和625%.

(a)保护层对黏结强度的影响

(b)保护层对峰值滑移的影响图9 保护层厚度对黏结强度和峰值滑移的影响Fig.9 Effect of concrete cover on bond strength and corresponding slip
图10所示为保护层厚度对平均黏结应力-滑移曲线的影响.由图可知:不同保护层厚度的曲线走势基本一致.当保护层厚度较小时,试件发生劈裂破坏,峰值过后黏结应力下降较快,曲线与坐标横轴包围的面积相对较小.当保护层厚度较大时,试件发生拔出破坏,随着保护层厚度的增加,曲线与坐标横轴包围的面积越来越大,表明试件的耗能能力增强.由表4可知,保护层厚度从1d增加至3d时,拐点之前平均黏结应力-滑移曲线下围成的面积比例为:0.61∶0.68∶0.79∶0.82∶0.87.
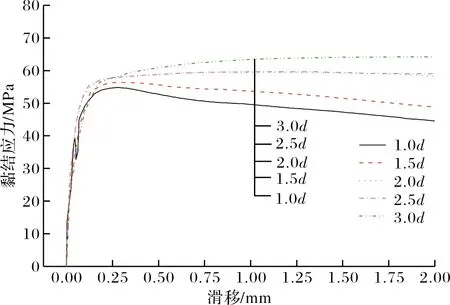
(a)上升段曲线
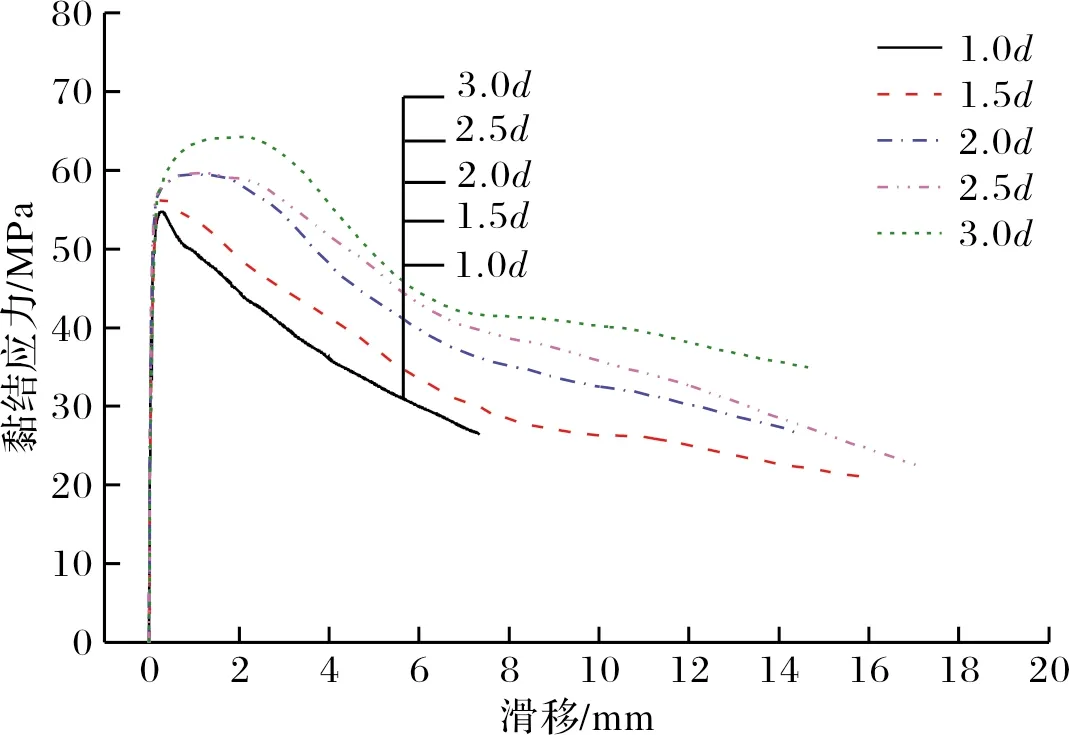
(b)完整曲线图10 保护层厚度对平均黏结应力-滑移曲线影响Fig.10 Effect of concrete cover on average bond stress-slip curves
3.4 黏结强度计算
由上述分析可知:钢筋直径、黏结长度以及保护层厚度对黏结强度均有影响,即黏结强度与钢筋直径以及保护层厚度成正比,与黏结长度成反比,并且钢筋直径影响较大.基于此,本文根据所有发生拔出破坏试件的试验数据进行统计回归分析,建立了钢筋与UHPC黏结强度计算公式.基于此,本章根据15组试验数据统计分析,得到的黏结强度表达式如下:
(3)
式中:τu为黏结强度;c,d,l分别为保护层厚度、钢筋直径和黏结长度;ft为UHPC抗拉强度.上式单位为:MPa和mm.
将式(3)的黏结强度计算结果与试验结果对比,结果见表5和图11所示.黏结强度计算值与试验值之比的平均值为1.00,变异系数为0.04.由图表可见,计算结果与试验结果吻合较好.

表5 计算值与试验值对比

图11 计算值与试验值比较Fig.11 Comparison of calculated values with experimental results
4 黏结应力-滑移本构关系
黏结应力-滑移本构方程可以综合反映钢筋与UHPC的黏结性能,同时也是对钢筋混凝土结构或构件进行数值分析的基本参数,所以有必要建立钢筋与UHPC黏结-滑移本构方程.本文根据试验实测得到的黏结-滑移曲线,分析曲线的特点,建立了拐点之前,黏结应力-滑移本构方程,其表达式如下:
(4)
式中:τu,τr分别为黏结强度和下降段拐点处的黏结应力值;su,sr分别为峰值滑移和拐点处滑移值.τu,τr,su,sr的表达式根据试验数据统计回归得到,表达式如下,式中单位分别为 MPa和mm.式(4)中α=0.05由曲线拟合得到.
(5)
(6)
(7)
(8)
图12所示为上述本构方程曲线与试验实测黏结应力-滑移曲线对比.由图可知本构方程与试验曲线吻合较好.

(a)第1组

(b)第2组
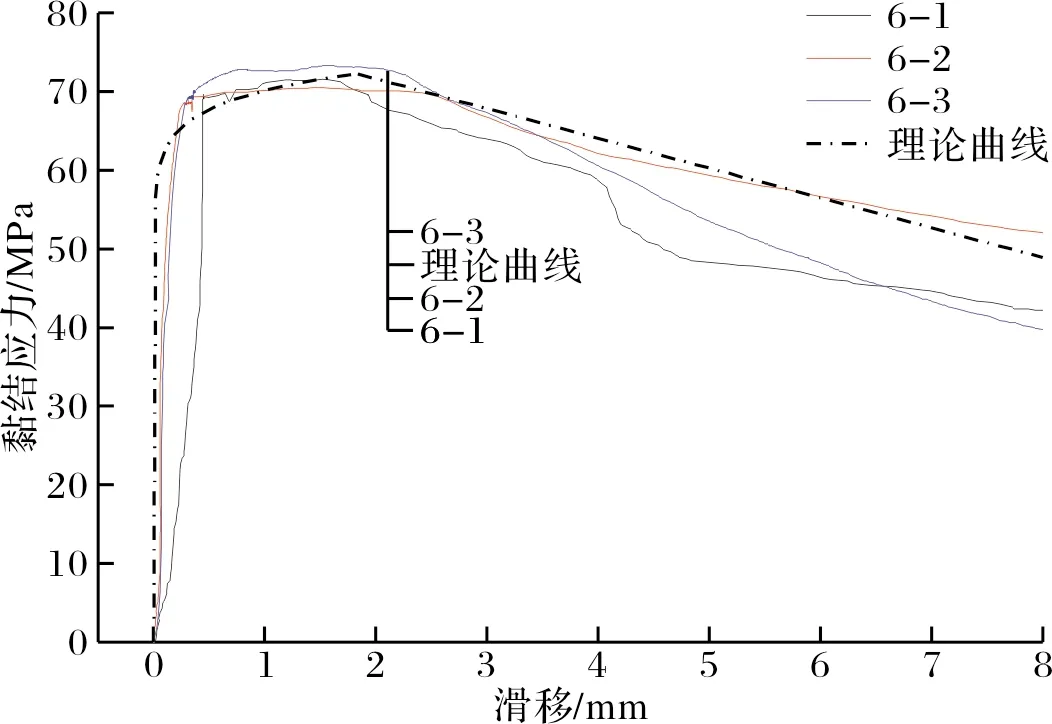
(c)第6组
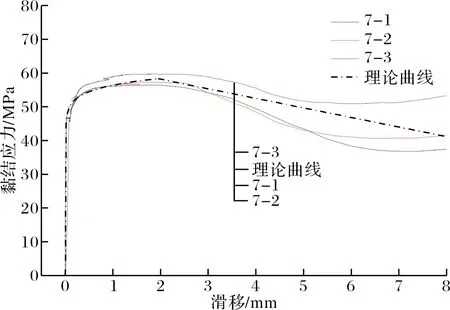
(d)第7组

(e)第11组
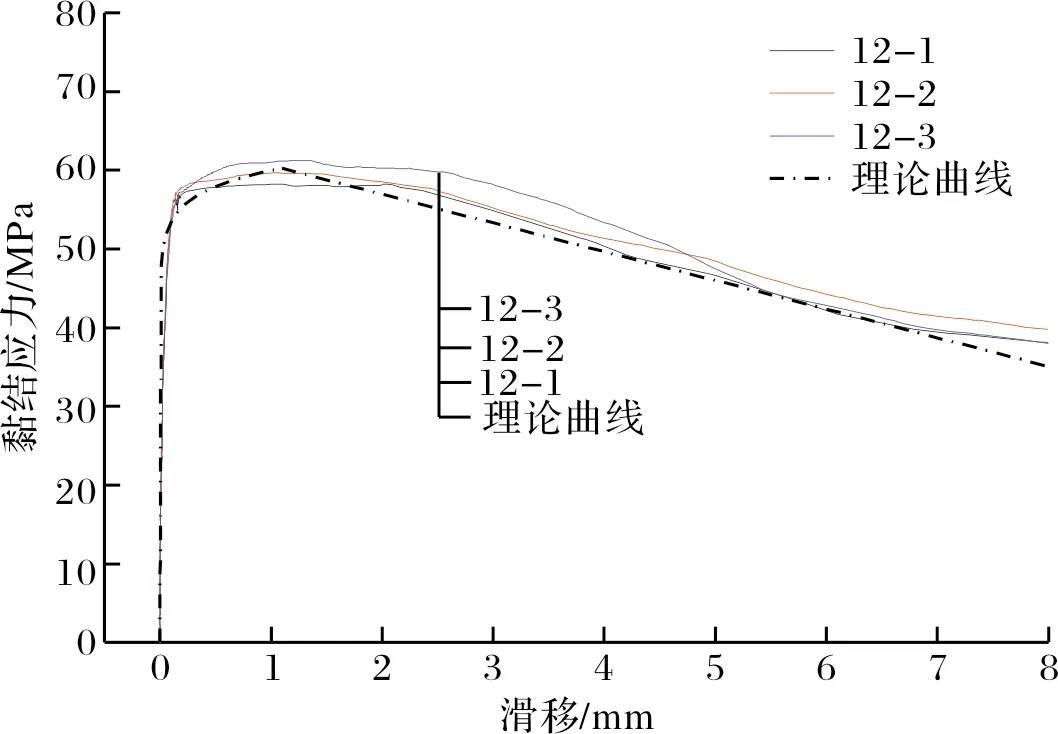
(f)第12组图12 拟合曲线与试验结果对比Fig.12 Comparison of experimental curves with fitting curves
5 黏结强度理论计算
本文通过对拔出试验破坏机理分析,结合弹性力学理论建立钢筋与UHPC黏结强度理论计算公式.
变形钢筋与混凝土的黏结作用主要由三部分组成:化学胶着力、机械咬合力以及摩擦力.当钢筋承受的荷载较小时,钢筋与混凝土之间没有发生相对滑移,荷载主要由化学胶着力抵抗;随着荷载的增加,钢筋与混凝土之间产生相对滑移,化学胶着力消失,荷载主要由钢筋肋与混凝土之间的机械咬合力以及两者之间的摩擦力共同抵抗.故黏结强度实际由机械咬合力和摩擦力两部分组成,基于此本文分别对机械咬合力和摩擦力进行计算.
机械咬合力的计算本文参考Tepfers厚壁圆筒力学模型[20]中部分弹性状态解计算机械咬合力.其计算公式如下:
(9)
式中τu1表示钢筋横肋引起的机械咬合力.
钢筋与UHPC之间的滑动摩擦力根据下式进行计算.
σf=μσN
(10)
式中:μ表示钢筋与混凝土之间的摩擦系数,压力σN主要由两部分组成,分别是:UHPC收缩引起的钢筋与UHPC之间的界面应力以及钢筋拔出过程中泊松效应引起的界面应力,其中钢筋的泊松效应引起的是负效应.根据弹性力学理论[21-22],求得钢筋与UHPC界面摩擦力表达式如下.

(11)

将上述机械咬合力以及摩擦力两个表达式相加之后得到钢筋与UHPC黏结强度理论计算值表达式为:

(12)
上述计算公式中UHPC力学性能参数,如抗拉强度、弹性模量、泊松比等,参考课题组前期试验结果取值.本文所用钢纤维长度、形状、养护条件与文献[23]中相似,故UHPC收缩值取该文献中常温养护UHPC收缩试验结果.变形钢筋与UHPC界面间的摩擦系数参考文献[24-25]取为1.05.
将试验参数代入上述理论计算公式,将计算值与试验值进行比较,计算结果见表6、图13所示.计算值与试验值之比的平均值为0.99,变异系数为0.01,由图、表可知,计算值与试验值吻合良好,可以用计算值近似代替试验结果.
为验证上述计算公式的有效性,作者共收集到37组满足计算条件的国内外相关试验数据[7,10-11],如图14(a)所示.现用上述计算公式计算所有的试验数据,计算结果列于表9中,计算值与试验值的平均值为0.99,变异系数为0.26,计算值与试验值的对比如图14(b)所示.由图、表分析可知上述理论计算公式可以较好的预测变形钢筋与UHPC材料发生劈裂破坏时的黏结强度.
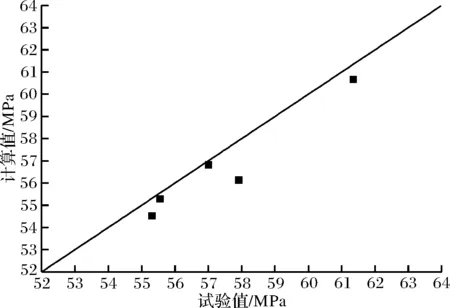
图13 计算值与试验值对比Fig.13 Comparison of calculated values with experimental results

(a)试验数据

(b)计算值与试验值对比图14 理论值与试验值对比分析Fig.14 Comparison of calculated values to experimental results
由于上述黏结强度理论计算表达式较复杂,不利于工程应用,故本文建立了黏结强度简化计算公式如下.
(13)
该式的第一部分反映钢筋横肋的机械咬合力,第二部分反映钢筋与混凝土之间的摩擦力大小,摩擦力与混凝土收缩值以及钢筋与混凝土之间的摩擦系数相关.用简化之后的公式计算粘结强度并与试验值比较,比较结果如图15所示,计算值与试验值之比的平均值为0.93,变异系数为0.27,简化之后的计算结果与精确解之间差异较小.该式物理意义较明确,可以用来近似计算钢筋与UHPC发生劈裂黏结破坏时的黏结强度.
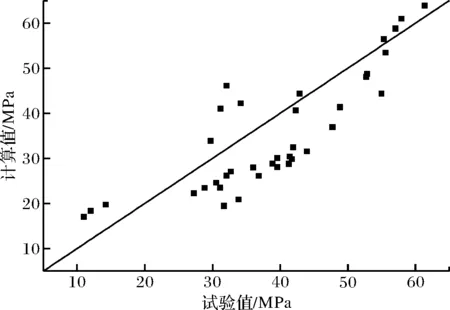
图15 理论值与试验值对比分析Fig.15 Comparison of calculated values to experimental results
6 结论
本文通过立方体拔出试验研究了钢筋直径、黏结长度、保护层厚度以及钢筋等级四个参数对钢筋与UHPC黏结性能的影响.从上述试验分析中可得出如下结论:
(1)与普通混凝土相比,UHPC显著提高了两种材料的黏结强度.此次试验中实测得到的钢筋与UHPC黏结强度在48~73 MPa范围内,约为普通混凝土的6~10倍.
(2)保护层厚度对试件的破坏形式有重要影响.当保护层厚度较薄时,钢筋拔出过程中产生的径向分力将使保护层劈裂,降低黏结强度.保护层厚度足够时,试件发生钢筋从混凝土中拔出的黏结破坏形式.
(3)钢筋与UHPC的黏结应力-滑移曲线非常饱满,曲线与坐标横轴围成的面积较大,表明钢筋拔出过程中消耗的能量较多.
(4)根据试验结果建立了钢筋与UHPC黏结强度计算公式以及黏结应力-滑移本构方程,且理论计算结果与试验结果吻合较好.
(5)根据钢筋与UHPC黏结机理分析结合弹性力学理论,建立了发生劈裂黏结破坏试件黏结强度理论计算公式,理论计算结果与试验结果吻合较好.
