代数函数域上快捷恢复LRC码的构造
2021-09-22吴珊珊
吴珊珊
(安庆师范大学数理学院,安徽安庆246133)
在大数据时代背景下,数据的传输呈指数型爆炸增长,若想有效地存储数据,就得引入冗余和编码技术。最简单的冗余形式就是复制,但复制会带来大量存储空间的消耗[1]。纠删码是存储系统容错的主要方法[2],但是其容错能力和运算效率存在缺陷。擦除码较复制而言,冗余和可利用性得到提高,只需较小的存储开销就能实现较高的数据可利用性,但其恢复丢失的冗余效率仍然较低。关于擦除码,学者重点关注擦除码的可恢复的局部性[3],即发现码的一种局部恢复性[4],从而研究一类具有局部性的最大可恢复码,并对局部可恢复码(LRC)及其参数展开研究。考虑长度为n、带有k个信息符号的码,若码字的第i个符号丢失,可以通过访问至多ri(ri≪n)个其他符号来恢复,则称该码具有良好的局部性ri。
因为大部分的码不具有良好的局部性,且可以直接使用的LRC码的构造太少,所以,LRC码成为研究热点。2011年,Gopalan等通过深入地研究线性码中冗余、擦除校正与符号局部性的关系,发现了码的距离上界和具有局部性的码符之间的关系,开创了码符局部性的理论研究[3]。随后Papailiopoulos证明了Gopalan等提出的局部性码符之间的确存在一种关系,并且在(r+1)|n的条件下是可以实现的,进而给出了LRC码的定义、构造、距离上界及速率上界等参数上界结论[4]。Gopalan等发现少有对码的另一个参数字母表大小的研究,于是从码字符号的局部性研究中发现了与字母大小相关的码的最小距离上界[5]。2013年,Silberstein等在Gopalan和Papailiopoulos的结论上又提出了一种新的LRC码族的构造[6],他们不仅将Gopalan提出的数量LRC码推广到向量LRC码,而且这个新的LRC码族的构造与Papailiopoulos提出的构造相比具有全符号局部性,利用这种全符号局部性构造得到的码可以更准确、更有效地恢复丢失的节点。2014年至2016年期间,Tamo和Barg等先后提出了LRC码族的概念,构造了当r+1|n时达到界的最优LRC码[7]。
以上研究在有限域、代数曲线、代数曲面及一些著名函数域上构造LRC码可以得到局部性更小的、速率更大的码,实现较低的恢复成本,但是它们的构造复杂、译码困难,因此,本文在代数函数域上构造LRC码,且这类LRC码的恢复过程只需经过一次减法运算。
1 预备知识
我们对于LRC码的构造完全基于代数函数域上,相关理论和符号来自于《代数函数域与码》[8]。现给出代数几何码的定义和3个命题,其中,代数几何码是构造LRC码的基础。
设C是有限域Fq上的码,下面给出局部恢复码的定义。
定义2[7]对任意的i∈[n]:={1,2,3,…,n},存在子集Ai⊂[n]{i}, ||Ai≤r和函数φi,使得对每个码字x=(x1,x2,x3,…,xn)∈C,都有xi=φi({xj,j∈Ai}),则称码C⊂Fnq是具有局部参数r的局部恢复码。
若用(n,k,d,r)和[n,k,d,r]分别表示码长为n、码的个数为qk、码的最小距离为d、局部参数为r的码和线性码,则LRC码的参数具有以下重要性质。
定理1[4]设C是在Fq上的[n,k,d,r]LRC码,则

当式(2)取等号时,C叫做距离最优LRC码。局部参数r满足1≤r≤k,且当r=k时,

命题1[8]考虑函数域F K和多项式φ(T)=anTn+an-1Tn-1+an-2Tn-2+…+a0,其中ai∈F。假设存在位P∈PF,对于i=1,2,3,…,n-1,vP(an)=0,vP(ai)≥0,vP(a0)<0且gcd(n,vP(a0))=1,则φ(T)在F[T]上是不可约多项式。
命题3[8]设K=Fq2是势为q2的有限域,H=Fq2(x,y),其中q是一个素数的幂,x和y满足xq+x=yq+1,则H被定义为在Fq2上的Hermite函数域,且H在K上有q3+1个次数为1的位,即对∀β∈K,存在q个元素α∈K使得αq+α=βq+1。
2 在代数函数域上构造局部恢复码

从而h至多有l⋅deg E+(l-2)⋅deg(x)∞个零点。同样可以证明,对任意的f∈V,f至多有l⋅deg E+(l-2)⋅deg(x)∞个零点,因而每个码字的重量
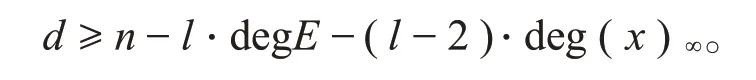
最后证明维数。
由于f∈V至多有l⋅deg E+(l-2)⋅deg(x)∞个零点,l⋅deg E+(l-2)⋅deg(x)∞ 又C是线性的,所以d≥n-l⋅deg E-(l-2)⋅deg(x)∞。 在Hermite函数域上构造具体的LRC码之前,我们需要介绍两个引理。 引理1若L(T):=Tn+a1T+a0∈Fq[T]是Fq上的三项式,x1,x2,x3,…,xn是其在Fq的扩域上的n个根,记其初等对称多项式为 记对称多项式Sk=x1k+x2k+x3k+…+xnk(0≤k≤n),则对于1≤k≤n-2时,有Sk=0。 证明对于k≤n,由Newton公式[9]知,Sk和σk之间有以下关系: 由于L(T)=Tn+a1T+a0是三项式,利用根与系数的关系[10]有: 当1≤k≤n-2时,都有Sk=0。 最后一步等式是由Char Fq|l得到的。 类似地,将引理2运用到定理2,得到码的局部恢复性定理。 设F=Fq(y)是有理函数域,F′=F(x)=Fq(y)(x)是F的单扩张,扩张次数[F′:F]=l且Char Fq|l,对于A(T)∈Fq[T],a0,a1∈Fq,有xl+a1x+a0-A(y)=0。对于任意的j=1,2,3,…,s,βj∈Fq,Pβj是F′F中完全分裂的位,即对∀i=1,2,3,…,l,Pαi,βj是Pβj的l个扩张。F的有理位构成集合S:={Pβ1,Pβ2,Pβ3,…,Pβs},Aj:={Pαi,βj:1≤i≤l},F′的有理位构成集合P:={Pαi,βj:1≤i≤l,1≤j≤s},则|P|=ls。 设E∈Div(F)是F中使得supp(E)⋂S=∅的除子,{f1,f2,f3,…,fm}是L(E)的一组基。设x∈F′使得{1,x,x2,…,xs-2}在F上线性无关且vPαi,βj(x)≥0,定义函数空间 记C:=Im(ev)是其映射的像,由代数几何码的定义知C是线性码。 定理3上述构造的码C是Fq上的[n,k,r]LRC码,其参数为 证明由定理2知,C是Fq上的[n,k,d]码,且各参数满足式(11)。对∀f1,f2∈V,λ,μ∈Fq,若 则λc1+μc2=((λf1+μf2)(Pα1,β1),(λf1+μf2)(Pα1,β2),(λf1+μf2)(Pα1,β3),…,(λf1+μf2)(Pαl,βs))∈C,因此C是Fq上的线性码。 下面证明C是局部恢复码。 对于码字c中的每个坐标值ci都可以被其它l-1个坐标值来恢复,因而C是局部恢复码,并且其恢复仅用一次减法即可得到。 与插值多项式解码进行对比,不难发现利用插值多项式构造更为复杂。而经过改进得到的局部恢复性定理,只需使用一次线性运算就能进行解码。 下面将上述定理应用于具体的Hermite函数域上。 并且这类LRC码可以通过一次线性减法运算进行快速恢复。 下面结合上述定理和引理,对本例进行一些说明。 令φ(T):=Tq+T-yq+1∈F[T],根据命题1,显然φ(T)是x在F上的极小多项式:因为vP∞(y)=-1,vP∞(1)=0 ,vP∞(-yq+1)=vP∞(yq+1)=(q+1)⋅vP∞(y)=-(q+1)<0 ,φ(x)=xq+x-yq+1=0 且gcd(q,vQ(-yq+1))=gcd(q,(q+1))=1,所以φ(T)是x在F上的极小多项式且degφ(T)=[F′:F]=q。 对任意的β∈K,多项式φα(T):=Tq+T-βq+1恰有q个互不相同的根:因为φα′(T)=q⋅Tq-1+1=1,故gcd(degφα(T),degφ′α(T))=1,因此φα(T)无重根。再由命题3知,对任意的β∈K,都存在q个元素αi(i=1,2,3,…,q)∈K都有等式αiq+αi=βq+1成立,显然是φα(T)=0的q个根,因此φα(T)有q个互异的根。对所有这样的(αi,β),都存在唯一的次数为1的位P′αi,β∈PH,即存在q个不同的具有性质P′αi,β|P′β的位P′αi,β∈PH,故可验证P′βj(j=1,2,3,…,q2)∈H/K是完全分裂的。对任意的P′βj(j=1,2,3,…,q2),将其q个扩张记为A′j:={ P′α1,βj,P′α2,βj,P′α3,βj,…,P′αq,βj},将H中除Q∞以外的q3个有理位构成的集合记为P′:={P′αi,βj:1≤i≤q,1≤j≤q2}。因为E=q(q-1)Q∞,故L(E)=L(q(q-1)Q∞),ℓ(E)≥deg E+1-g= 所以有deg E=q(q-1)>2g-1=q(q-1)-1,从而 综上所述,本文首先在代数函数域上构造了一类局部修复码,然后给出它们的参数,接着证明丢失的码字c=(c1,c2,c3,…,cn)坐标值ci满足ci=-,其中l是扩张次数,cik(k=1,2,3,…,l-1)是码字c中的l-1个分量,故可利用三项式的一次线性减法运算去恢复其他丢失的位置。通过一个具体的例子,阐明了在具体的Hermite函数域上如何利用一个三项式上的代数函数域构造一类LRC码及其快捷恢复。将本方法进一步推广到Kummer扩张、Artin-Schreier扩张等代数函数域上,也一样可以得到较好的结果。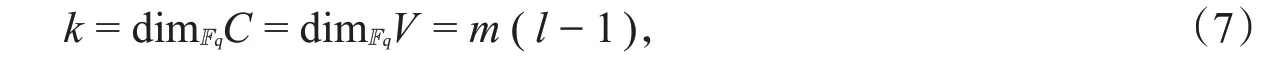

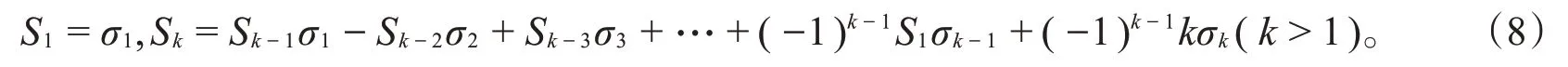






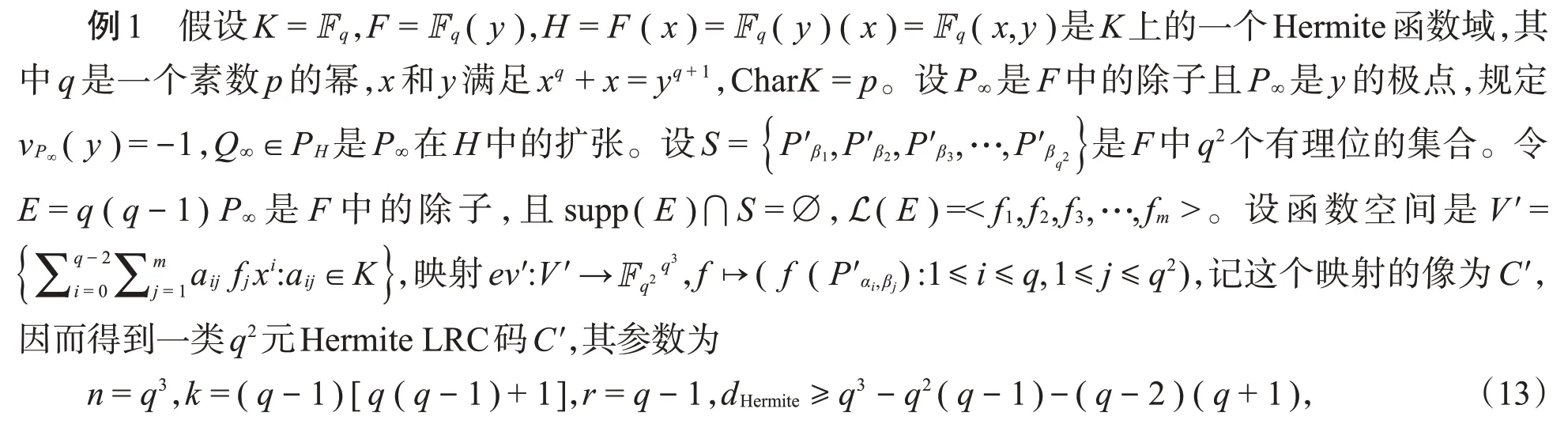
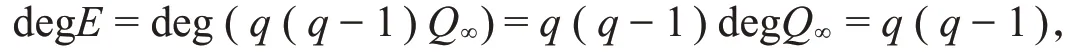

3 结束语
