压电纤维复合材料作动行为研究

陈 浩，涂建维，张家瑞，李 召

(武汉理工大学 道路桥梁与结构工程湖北省重点实验室，武汉 430070)

在减振降噪和结构振动控制领域，压电材料因其优良的作动特性而得到广泛关注。压电陶瓷是常见的压电智能材料，具有灵敏度高、温度稳定性好等优点，但其质地脆、柔韧性差且压电效应低。为此，美国国家航空航天局兰利研究中心研发了新型压电纤维复合材料——宏纤维复合材料(MFC)[1]。MFC主要由压电陶瓷纤维、环氧树脂基和叉指电极组成，可以通过逆压电效应实现其作动性能。

在航空航天领域，MFC被广泛应用于板壳结构变形、减振控制。PARADIES et al[2]将MFC与机翼整体建模进行数值计算，并对粘贴有MFC的机翼模型进行了静力、动力试验。CHEN et al[3]在MFC对飞机尾翼抖振的控制方面进行了研究，结果表明MFC可以有效减小尾翼的抖振。

上述研究表明，获得精确的MFC作动力公式对研究MFC的应用十分重要。目前，多采用有限元整体建模与仅考虑弯曲变形的等效简化计算方法研究MFC作动力。GUO et al[4]在MFC作动力计算中仅考虑了MFC与结构的弯曲变形，完成了MFC复合梁结构的振动控制试验。PRASATH et al[5]使用“混合规则”的概念和串并联电容理论进行压电有限元仿真，分析MFC作动性能并通过试验进行了验证。ZHANG et al[6]基于等效参数和弯曲变形理论，推导了MFC的作动力和弯矩公式。但上述研究由于忽略了MFC与结构的剪切变形，仿真精度低且不能体现MFC作动力在粘贴界面上的剪切滞后现象。

在板壳结构的研究中，剪切变形理论已被广泛应用[7-8]。MFC复合结构可被视为层合板结构，层合板结构剪切变形不可忽略。三阶剪切变形理论(TSDT)精确度高，可以很好地模拟层合板结构的变形[9]。因此，本文运用TSDT推导了MFC的作动力公式，以文献[10]中的MFC复合梁结构为例完成了作动仿真与试验的对比分析。研究表明，基于TSDT的MFC作动力公式计算精度高，可以应用于MFC复合结构的仿真分析。

1 基于TSDT的MFC作动力公式

选取极化方向与纤维排列方向平行的P1作动型MFC为研究对象，其结构如图1所示。MFC与平板结构的尺寸与粘贴关系如图2所示，坐标轴的原点位于平板的中心位置。其中，a、b分别为MFC的有效长度与有效宽度；t2为MFC上表面到平板中位线的距离；hp为MFC的厚度；2t1为平板结构的厚度；Es为平板结构的弹性模量；Gs为平板结构的剪切模量。

图1 P1作动型MFC结构示意图Fig.1 P1 actuation type MFC structure diagram

图2 MFC复合平板结构尺寸和粘贴关系示意图Fig.2 Schematic diagram of MFC composite panel structure size and pasting relationship

假定结构法线方向的位移v(x,z)与z无关，MFC粘贴位置处的轴向位移可表示为：

(1)

式中：v(x)为平板结构的挠度；u0(x)为平板结构沿x轴的轴向位移；φx(x)为截面绕x轴的转角；hx(z)为x方向上沿厚度的位移分布函数，用于表示截面剪应变沿厚度的分布。

由于MFC与平板结构材料属性不同，我们分别定义整体位移分布函数hg(z)与局部位移分布函数hl(z)，来满足MFC与平板结构变形协调与应力平衡条件。MFC复合平板结构截面的位移分布函数可用下式表示：

(2)

式中：j1、j2、k1、k2表示局部位移分布函数的相关参数，ξ1、ξ2表示截面的局部坐标。

MFC与平板结构为单面粘贴形式，忽略粘贴层厚度，MFC与平板结构完全黏合[11]。MFC的下表面与平板的上表面粘贴，则MFC上表面与平板下表面的剪应力为0 N.根据变形协调条件可知，MFC与平板结构粘贴界面的剪应力应相等，且位移应保持连续。可以得到局部位移分布函数中的相关参数如下式：

(3)

式中：Gp为MFC的剪切模量，由式(1)可以得到MFC在xz平面内的剪应变：

(4)

式中：ut1与ut2分别表示MFC在z=t1与z=t2位置处沿x轴方向的位移。

在x轴方向上，建立z=t2位置处MFC的应力平衡方程：

(5)

式中：σpx,t2表示z=t2位置处MFC沿x轴方向的正应力。

以平板结构为研究对象，可以得到平板结构在xz平面内的剪应变：

(6)

式中：u-t1表示在z=-t1位置处平板结构沿x轴方向的位移。

在x轴方向上，建立z=t1位置处平板结构应力平衡方程：

(7)

式中：σsx,t1表示在z=t1位置处平板结构沿x轴方向的正应力。

联立式(1)、式(4)与式(6)并化简，可以得到：

(8)

联立式(7)和式(8)消除平板结构沿x轴方向z=-t1位置处的位移u-t1，可以得到：

(9)

由于MFC传递的剪应力大部分发生在MFC边缘位置(x=±a/2，y=±b/2)，MFC除边缘位置外正应变分布保持恒定[12]。假定MFC复合平板结构沿x轴方向的曲率为常数，联立式(5)与式(9)可以得到z=t2位置处MFC和z=t1位置处平板结构应变偏微分方程组：

(10)

在电压作用下，MFC内力呈对称分布且边缘位置正应力为0 N，因此，MFC沿x轴方向的正应变也呈对称分布。可以得到z=t2位置处MFC应变分布通解：

(11)

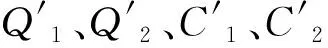
MFC的本构方程[13]可以表示为：

(12)

式中：Ep为MFC沿x方向的弹性模量；Ex为施加于x方向的电场强度；d33为在x轴方向单位电场作用下，MFC在x轴方向产生的应变。

MFC复合平板结构是对称的，在作动方向上，MFC复合平板结构的中线位置无剪切变形[14]。文献[15-16]采用CPT与TSDT两种方法计算得到的平板结构挠度与x方向轴向位移几乎是相等的。为此我们采用CPT计算得到平板结构曲率与轴向应变，然后再代入式(1)中，可以求得z=t2位置处MFC中线位置沿x轴方向的应变εpx,c：

(13)

(14)

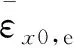
(15)

图3 MFC边缘位置上表面微元应力示意图Fig.3 Schematic diagram of the micro-element stress on the upper surface of MFC edge

将式(13)与式(15)代入式(11)中，可以得到沿x轴方向，z=t2位置处MFC的应变：

(16)

联立式(4)、(5)与(16)，可以得到MFC沿x轴方向的作动应力，即MFC与平板结构界面(z=t1)处沿x轴方向的剪应力：

(17)

(18)

由于式(18)中的参数均与平板结构弹性模量及厚度有关，因此本文提出的MFC作动力公式同样可以反映出MFC作动性能与平板结构弹性模量及厚度的关系。为了进一步探究三者之间的关系，我们以在1 500 V电压下工作的M2807-P1型MFC为例，取平板结构弹性模量为20 GPa，分析了x轴方向的MFC总作动力及总作动弯矩与平板结构厚度之间的关系；取平板结构厚度为20 mm，分析了x轴方向的MFC总作动力及总作动弯矩与平板弹性模量之间的关系，具体如图4所示。

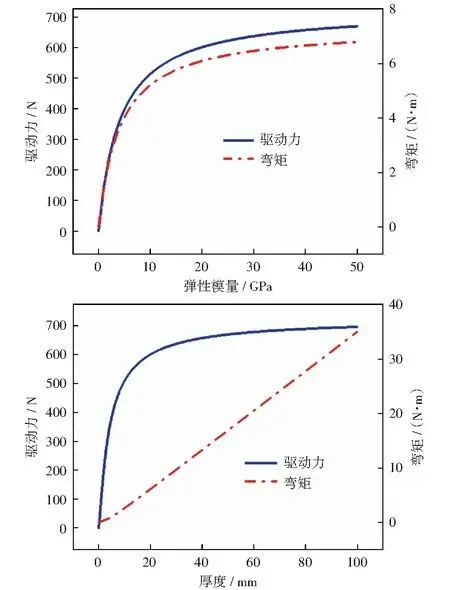
图4 MFC作动性能与受控结构厚度及弹性模量的关系Fig.4 Relationship between MFC performance and controlled structure thickness and elastic modulus

从图4可知，MFC的总作动力增长速度随平板结构的弹性模量与厚度的增大逐渐放缓并趋于稳定。MFC总作动弯矩随厚度增大而骤增，但随平板结构弹性模量增长的速度较慢。MFC的作动力与结构的弹性模量及厚度呈现非线性关系，MFC作动弯矩与结构厚度呈现线性关系，与结构弹性模量之间呈现非线性关系。这说明了MFC的作动性能不仅取决于MFC的材料参数与工作电压，还依赖于平板结构的厚度与弹性模量。

2 MFC复合梁结构仿真分析

为了验证本文推导的基于TSDT的MFC作动力公式的适用性，我们以文献[10]中的MFC复合梁结构作动试验、作动仿真为例进行了分析。文献中采用的是M2807-P1型MFC，MFC复合梁结构粘贴情况和有限元模型如图5所示。

图5 MFC复合梁结构粘贴情况与有限元模型Fig.5 Pasting situation and finite element model of MFC composite beam structure

M2807-P1型MFC与复合梁结构的材料参数如表1所示。运用基于TSDT的MFC作动力公式计算了P1型MFC在0～1 000 V电压下的界面剪应力分布，如图6所示。

表1 复合梁结构与MFC材料参数Table 1 Composite beam structure and MFC material parameters

图6 施加不同电压时MFC的界面剪应力Fig.6 MFC interface shear stress when different voltages are applied

由图6可知，在x轴方向上，P1型MFC边缘位置(x=±a/2，y=±b/2)的界面剪应力远大于中部的界面剪应力且其由边缘位置向中部呈现骤减趋势，剪应力分布呈现双曲正弦函数型。这是由于MFC与复合梁结构之间存在剪切滞后现象，边界处剪应力存在突变。这说明基于TSDT的MFC作动力计算公式可以准确地反映出MFC作动力的分布特点。由MFC的内力分布特点可知，MFC的剪切变形是作动力传递的主要因素之一。

文献[10]对粘贴有M2807-P1型MFC的复合梁结构进行了作动试验。本文对MFC施加0～1 000 V电压，研究复合梁结构在10种情况下的静态偏转值。首先在作动方向上以0.4 mm为计算长度，使用基于CPT[15]和TSDT的MFC作动力公式计算出MFC的分段作动力。然后在ANSYS中通过表面效应单元将其施加于对应的粘贴位置，对1.2 mm厚的MFC复合梁结构端部位移进行了仿真计算。最后将仿真结果与试验结果进行对比，具体如图7所示。

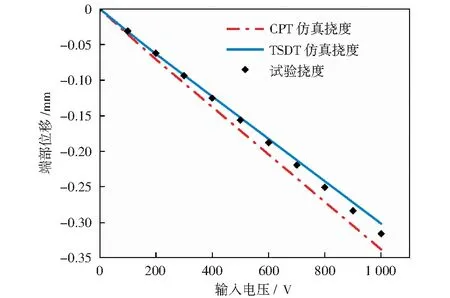
图7 MFC复合梁结构端部位移图Fig.7 MFC composite beam structure end displacement diagram

由图7可知，随着施加的电压增加，复合梁结构端部位移随之增大。基于TSDT的MFC作动力公式的仿真结果与试验结果的最大位移偏差为4.37%，而基于CPT的MFC作动力公式的仿真结果与试验结果的最大位移偏差为13.61%.这说明本文推导的基于TSDT的作动力计算公式是正确的，且精度高于基于CPT的作动力计算公式。

3 结论

本文基于TSDT推导了一种考虑剪切变形的MFC作动力公式，并通过仿真验证了其准确性和适用性，得出以下结论：

1) MFC的作动力与受控结构的弹性模量及厚度之间的函数关系为非线性，MFC的作动弯矩与受控结构厚度之间的关系为线性，与受控结构弹性模量之间的关系为非线性。

2) MFC在粘贴边缘位置界面剪应力较大，在中部位置界面剪应力迅速减小并趋于稳定。MFC与复合梁结构之间的界面剪应力分布呈现为双曲正弦函数型。

3) 基于TSDT的端部位移仿真结果与试验的端部位移时程曲线基本吻合，且优于基于CPT的仿真结果。本文推导的MFC作动力公式是适用的且计算精度更高，对MFC复合梁结构具有良好的作动效果，可以推广到板壳结构的减振领域。