基于粒子滤波算法的足底压力预测

曹 更，玄兆燕，李德恒，崔冰艳

（1.华北理工大学机械工程学院，唐山 063210；2.河北君业科技股份有限公司，唐山 063000）

引 言

随着临床康复系统的蓬勃发展，人体下肢运动目标检测、运动预测识别在康复机器人和康复训练中得到广泛的应用，下肢运动识别是临床决策支持系统的核心［1］。在下肢运动识别系统中，下肢运动识别可划分机械式运动识别、光学式运动识别、电磁式运动识别［2⁃4］和生物信息式识别。机械式运动识别通过机械仪器、位姿传感器获取运动数据，参考对照实验表进行识别，如穿戴外骨骼康复机器人运动识别；光学式运动识别通过搭载视觉相机或传感器，利用视觉三角测量方法对运动目标进行精准定位，如视觉定位识别机器人方面的研究；电磁式运动识别通过采集一种单自由度电磁振动能量进行运动识别；生物信息式识别通过采集生物力学和肌肉电信号，用于检测识别运动步态信息。与生物力学信息不同的是，光学式、运动识别方式普遍存在下肢运动识别稳定性差，易受环境因素影响的问题；电磁式运动识别计算方法复杂、耗时时间长；机械式运动识别对硬件要求高；而基于生物力学原理，采用足底压力可以准确地分析运动过程中的步态参数，探测人体下肢结构，评估和预测下肢运动轨迹，分析运动模式更加容易和可追踪。因此，对步态参数进行运动状态分析是生物信息式识别的关键要素。

人体运动预测是下肢康复机器人运动识别的关键环节，利用运动预测具备高估计精度和鲁棒性［5］的特点，采用相适应的预测算法是下肢运动预测的核心。传统的运动预测算法存在计算效率低、易于陷入局部极值等缺点［6］。为了提高预测算法的收敛精度［7⁃9］，采用算法控制器能够快速预测到最优路径，但目标跟踪算法难以适应目标场景变化。粒子滤波算法具有容易实现、收敛速度快等特点［10］，并在机器人运动、无人机路径预测规划运动预测领域得到应用。粒子集在重新采样后更接近目标的真实状态分布［11］，常用来解决非线性采样滤波问题。因此，粒子滤波器自适应更新提高了位置预测的准确度，使用该预测算法可以有效解决足底压力预测的非线性问题。根据步态周期的特性，建立非高斯信号的粒子滤波算法模型并在数据集上进行对比试验。粒子滤波算法广泛应用在运动目标跟踪定位、图像数据处理、通信和控制等领域［12⁃15］，同时也广泛应用于处理非高斯系统的问题。

为了研究下肢运动的路径规划和运动规律，提升康复训练的柔顺性，使用德国EMED 足底压力平板获取人体步态周期的运动状态下肢运动特征参数，有效区分步态周期，建立步态频率模型。同时，在采集足底压力的过程中，足底压力数据呈现出一种粒子集的形式，因此提出一种基于粒子滤波器的足底压力预测算法，预测下一时刻步态的足底压力，建立预测模型，以不同性别、身高、年龄的实验者的步态数据为研究对象，验证预测结果与测量结果足底压力的吻合性，从而为下肢运动预测提供技术和理论支撑。

1 步态周期模型

普通行走时，一个正常运动人完整的步态周期主要包括支撑期和摆动期，在正常运动的情况下，只有支撑期阶段存在足底压力，所以只考虑支撑期的足底压力状态。根据步态周期和步态频率等参数，将支撑期相位进行划分。支撑相步态周期分为支撑前期、支撑初期、支撑中期和支撑末期，如图1 所示。

图1 人体运动支撑相步态周期Fig.1 Gait cycle of human movement support phase

同时建立步态周期模型

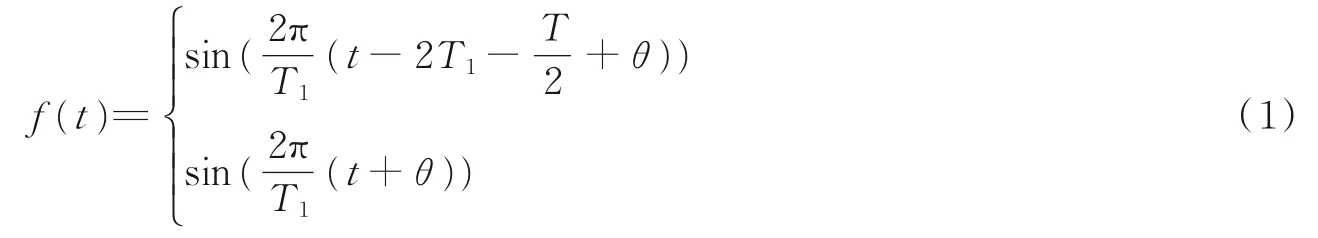
式中：T为步态周期，T1为支撑期时间，θ为初始相位角。在步态周期模型的基础上，建立下肢运动位移模型

式中：Xi+1表示X⁃Y坐标系下t时刻的足跟位置，L表示步长，ξ表示行进步向角。

以不同身高、体重、性别和年龄的实验者为研究对象，在EMED 足底压力平板上各采集步数为40帧步态进行数据分析，可得出以下结论。支撑初期为起始状态，约占整体运动10%；支撑中期为行进运动状态，时长为184 ms，约占整个步态运动周期的30%；支撑末期为运动的稳定阶段，时长为209 ms，约占整个步态运动周期的50%。为有效表达双足步态特征参数和时间的联系，获取了实验者下肢运动参数随运动周期的变化，结果如图2 所示。

图2 实验者运动过程中运动参数变化Fig.2 Changes of motion parameters during the movement of the experimenter

2 实验数据采集

实验者使用足底压力平板，检测足底压力信息变化，结果如表1 所示。在足底压力测量实验中，使用德国EMED 足底压力平板获取实验者运动过程中足底压力的原始数据，同时生成实验者的生物力学特征和运动特征参数。步态时空参数测量是常用的步态检测方法，以时间序列形式生成步态测量数据。下肢运动状态可用足底压力、足底接触面积和步态频率等来表达。步态特征提取就是从采集足底压力数据中识别有效特征的过程。通过EMED 平板采集足底压力，导入excal 生成某一时刻足底区域压力分布的图像，数字分布呈现出该时刻足底压力区域的受力情况，每一个粒子点代表足底压力区域的压力数值，这些粒子构成一个足底压力的粒子集，如图3所示。

表1 行走过程中运动特征参数Table 1 Motion characteristic parameters dur⁃ing walking

图3 足底压力粒子区域分布图Fig.3 Regional distribution of plantar pressure parti⁃cles

3 步态预测算法

下肢运动是无规则的非线性运动，在足底运动跟踪的过程中，核心就是解决足底位置更新问题。通过采集足底压力信息，分析足底压力与步态周期的关系，作为下肢运动状态的实时反馈。下肢预测问题建立在足底压力预测基础上，是非线性预测的主要研究内容。粒子滤波算法能利用提供的状态方程和观测方程对先验概率密度函数进行筛选，在已知足底压力粒子集的情况下，可利用贝叶斯定理结合先验概率密度函数，计算不同实验者情况下足底压力的先验概率，让足底压力粒子向高似然函数移动，排除极端数值足底压力粒子的影响，构成一个新的粒子集。粒子滤波算法建立在贝叶斯估计的基础上，利用带权值的足底压力粒子来拟合后验概率密度函数，对足底压力的状态进行预测，将满足预测条件的足底压力进行修正后输出，对不满足预测条件的重新计算先验概率密度函数，再次构建一个新的粒子群。粒子滤波算法可独立于步态周期模型，有效解决非高斯情况下下肢预测运动非线性估计问题，证实粒子滤波算法能有效解决非线性预测。

粒子滤波算法主要由初始状态、预测阶段和修正后重采样3 部分组成。初始阶段用足底压力粒子模拟粒子群，足底压力粒子在状态空间内均匀分布，进行粒子群初始化，计算初始时刻权重；预测阶段，先计算累积分布函数为先验概率密度函数，对主要受力部位进行筛选，消除无关粒子的影响，对足底压力粒子的位置进行估计，再根据足底压力粒子的状态转移方程进行足底压力预测，校正后重采样。足底压力预测采集的粒子数目越多，足底压力滤波精度越高。预测算法流程如图4 所示。

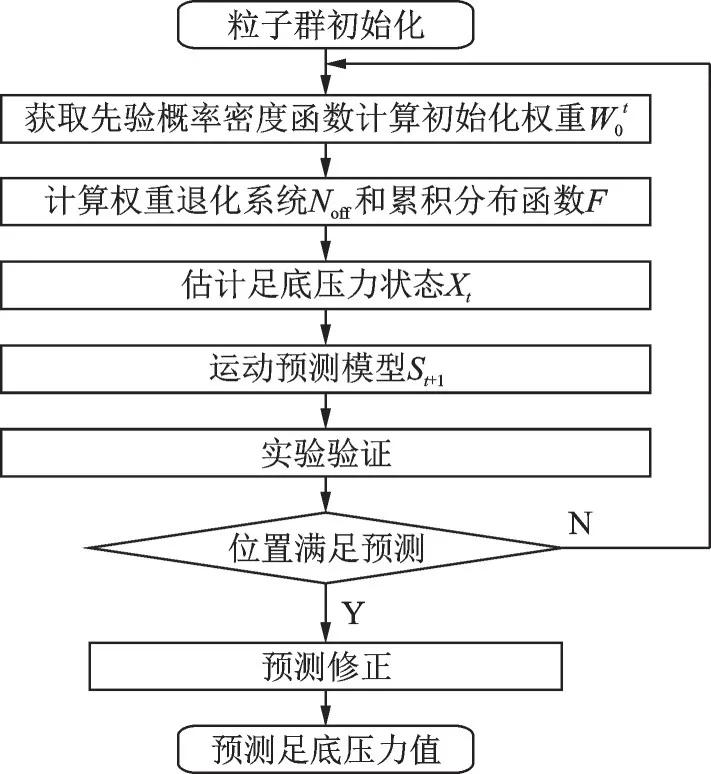
图4 粒子滤波预测算法流程图Fig.4 Flow chart of particle filter prediction algo⁃rithm

在此基础上，足底压力粒子滤波算法计算方法为：

（1）首先对粒子群进行初始化，从足底运动状态的先验概率密度函数中选取粒子集，计算初始化时刻权重。

式中：Wt为归一化的权重，N为粒子群初始化样本数。

（2）计算累积分布函数F为先验概率密度函数，消除权重小的粒子，重采样后的粒子集为xit。

式中：P（xi）为观测量Zt的似然函数，F-1为累计分布函数的逆函数，ui为服从［0，1］分布的随机变量。

估计足底压力状态Xt

（3）足底压力预测算法粒子滤波状态向量St由下肢运动状态参数构成，观测变量Zt为采集足底压力位置坐标，运动预测模型St+1。

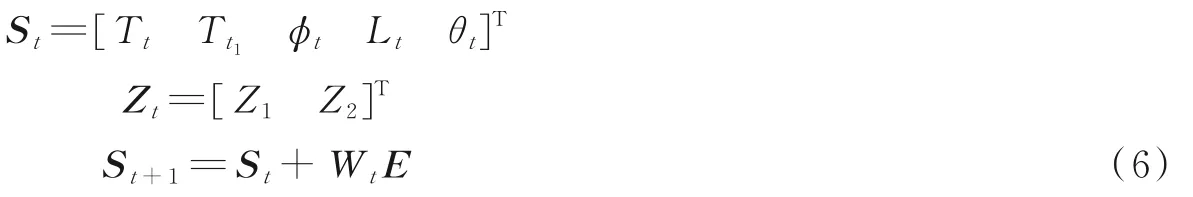
式中：T、φ、L和θ为步态特征参数，Z1和Z2为足底压力坐标位置。

（4）如果估计位置不满足实验检验，将采样粒子进行预测修正。在运动预测修正过程中，采样新的粒子，计算新的权重。

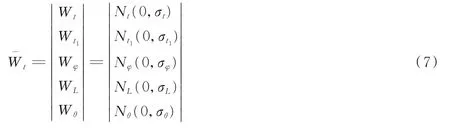
式中：σt、σt1、σφ、σL和σθ为根据采集的40 组步态频率参数样本数据的计算取值，在本次实验中的设定值如表2 所示。

表2 步态参数Table 2 Gait parameters

4 实验验证

为了验证足底压力预测算法的准确性，对此作了实验检测，步骤为：

（1）采集不同身高、体重、年龄和性别的正常运动者的步态分析数据作为实验对象。

（2）让实验者在同一压力平板上行走相同的步数，步数设置为40 帧，每个实验者在正常状态下行走，分为快走和慢走两组，并用足底压力平板采集数据。

（3）查看采集的足底压力信息，查阅相邻两次的步态长度和行进步相角度，由此可在步态模型基础上对足底压力进行预测。

（4）将采集实验者步态数据与预测数据进行对比参照，求出足底压力预测误差。

（5）对实验结论进行分析，计算实验者在平时正常运动状态下慢速和快速行走预测足底压力的准确率。

采集慢速和快速情况下的足底压力数据，同时分析足底压力预测系统的误差特性，保证实验过程中不存在任何电磁干扰，排除设备故障等因素。足底压力平板总长2.5 m，测试区域长度0.5 m。每组步态40 帧，为更好地验证粒子滤波算法预测足底压力状态的稳定性，分别选取5 名年龄、身高和体重存在一定差异的实验者，进行对照实验。利用1 号实验者自身对照，探究慢速和快速步态下预测算法的稳定性差异。在相同的步速下，利用3 号实验者和4 号实验者探究不同性别、体重对预测算法稳定性的影响。在相同的运动状态下，利用2 号实验者和5 号实验者的足底压力数据来探究不同年龄对预测算法稳定性的影响。实验者的人体信息如表3 所示。

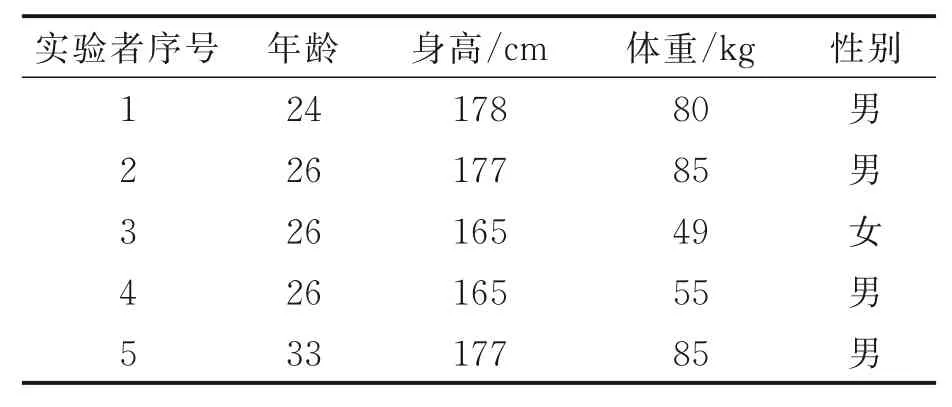
表3 实验者人体信息Table 3 Human body information of subjects

在不同步速下测量1 号实验者步态周期内足底压力数据：慢速行走运动时间114 s，步态速度115.8 mm/s；快速行走运动时间76 s，步态速度259.9 mm/s。足底压力实验值与估计值如表4 所示。通过表4 提取连续10 次相邻的足底压力数据，绘制1 号实验者在不同步速下试验测量值和算法估计值的步态数据曲线，形成慢速和快速运动的实验对照，验证不同运动状态对算法精度和稳定性的影响。不同步速下足底压力拟合变化趋势如图5（1）所示。为了验证不同步态速度的测试精度，分别计算绘制同一组实验者慢速和快速步速下足底压力数据误差曲线，结果如图5（2）所示。

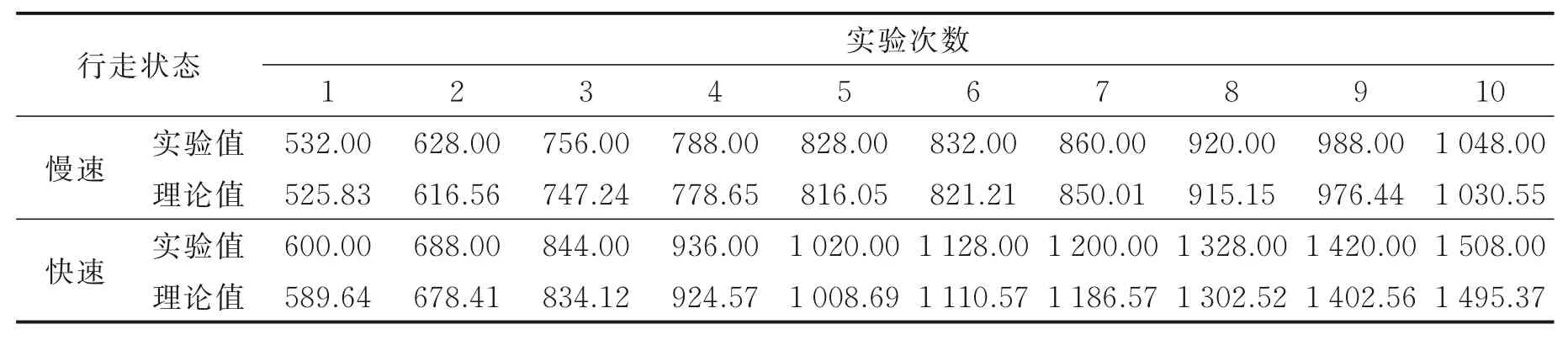
表4 实验者不同步速下步态数据Table 4 Gait data of experimenter at different walking speeds N

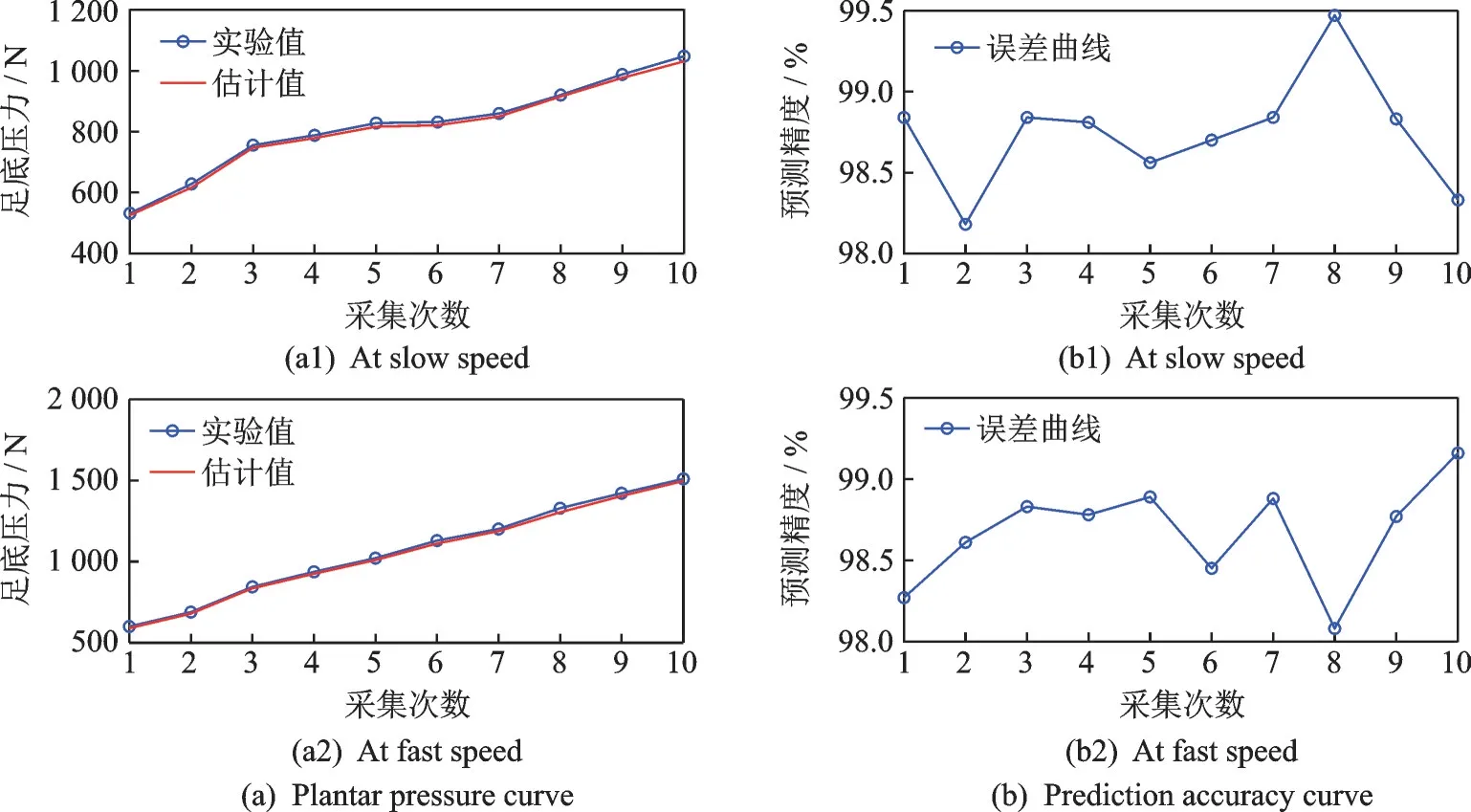
图5 不同步速下足底压力数值估计及其误差曲线Fig.5 Numerical estimation and error curve of planar pressure at different walking speeds

分析预测精度结果可知，在慢速行走和快速行走状态下，预测精度均在97.5% 以上，慢速行走状态下的预测精度优于快速行走状态，证明基于足底压力的粒子滤波算法更适合用于不同行走状态，同时证明算法精度比较稳定。

在相同步速和年龄下分别采集3 号和4 号实验者的足底压力数据，其中3 号女性实验者体质量49 kg，4 号男性实验者体质量55 kg。足底压力实验值与算法估计值如表5 所示。通过表5 提取连续10次相邻的足底压力数据，绘制3 号和4 号实验者在相同步速下的足底压力曲线，形成不同体重和不同性别的实验对照，验证不同体重和性别对算法精度和稳定性的影响，结果如图6（a）所示。将预测压力数值与实际压力数值进行对比，求出误差率，绘制预测精度曲线，结果如图6（b）所示，分析不同性别和体重对预测算法稳定性的影响。

表5 不同性别和体重实验者步态数据Table 5 Gait data of subjects with different genders and body weights N

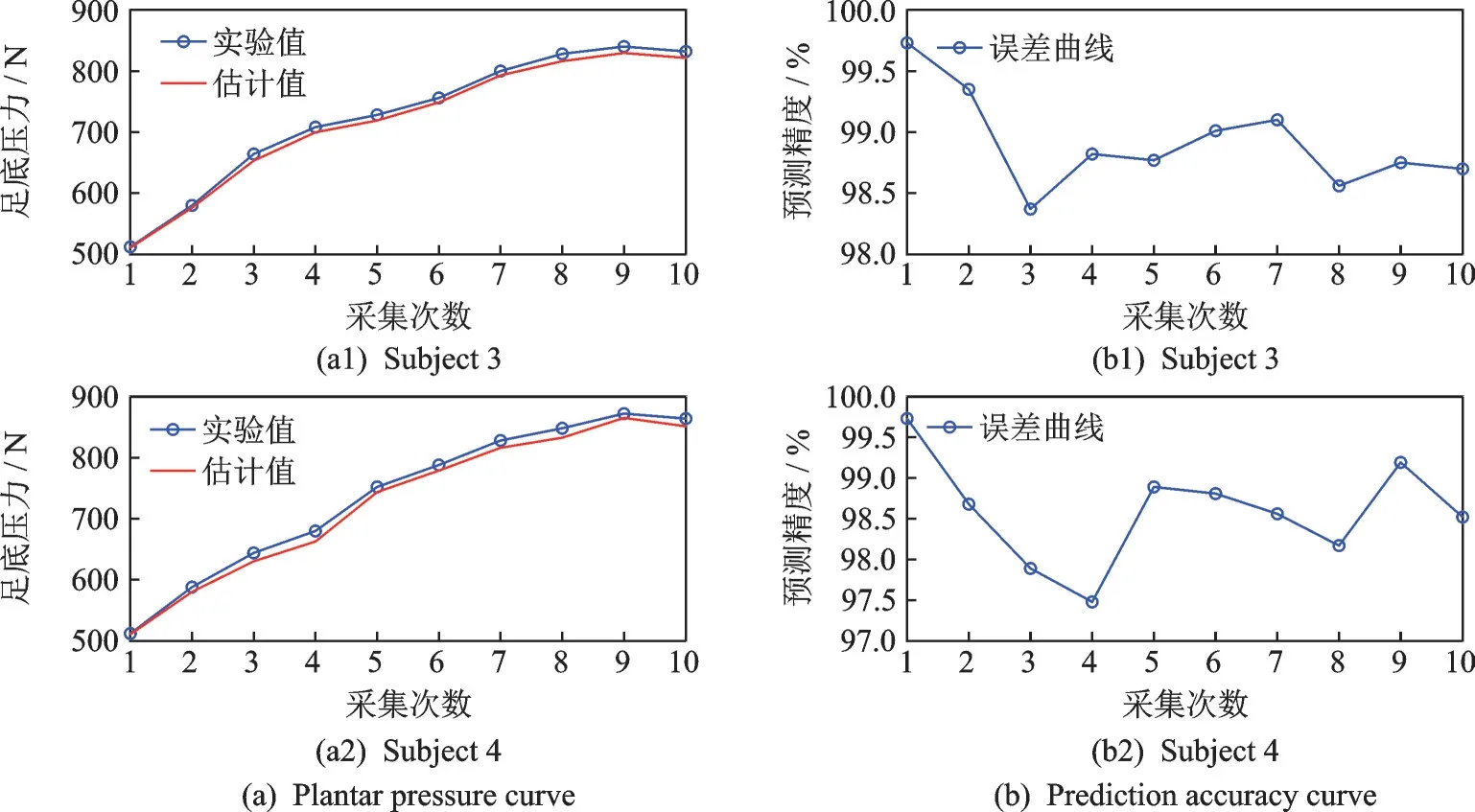
图6 不同性别和体重下足底压力数值估计及其误差曲线Fig.6 Numerical estimation and error curve of planar pressure for different genders and body weights

由预测精度的分析结果可知，在不同性别和体重状态下，预测精度均在97% 以上，证明性别和体重可作为影响足底压力粒子滤波算法稳定性的无关因素，较高的预测精度也验证了算法预测的可靠性。

在相同的步速、体重和身高条件下分别采集2 号和5 号实验者的足底压力数据，其中2 号实验者年龄26 岁，5 号实验者年龄33 岁。足底压力实验值与算法估计值如表6 所示。通过表6 提取连续10 次相邻的足底压力数据，分别采集2 号和5 号实验者的足底压力数据，绘制在相同运动状态下的足底压力曲线，如图7（a）所示。将预测压力值与实际压力值进行对比，求出误差，绘制预测精度曲线，结果如图7（b）所示，分析不同年龄对预测算法稳定性的影响。

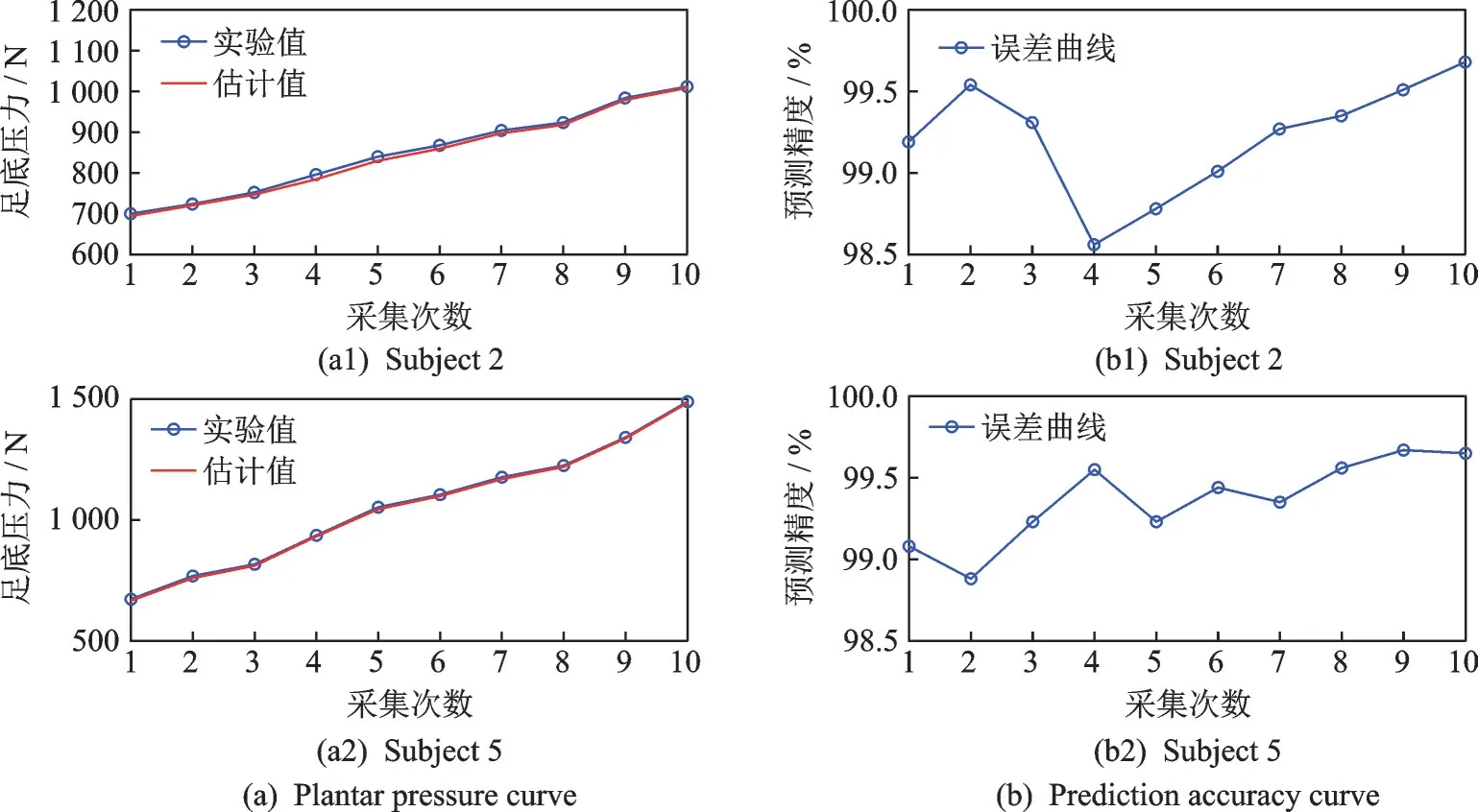
图7 不同年龄下足底压力数值估计及其误差曲线Fig.7 Numerical estimation and error curves of plantar pressure at different ages

表6 不同步龄实验者步态数据Table 6 Gait data of subjects of different ages N

由预测精度的分析结果可知，在不同年龄状态下，预测精度均在98.5% 以上，证明年龄可作为影响足底压力粒子滤波算法稳定性的无关因素，预测精度能验证粒子滤波预测算法的稳定性。

5 结束语

实验数据结论表明，建立在步态周期模型基础上的足底压力预测方法，提取足底压力关键压力点信息，对运动状态进行估计，采用粒子滤波算法进行修正检验，去除无关因素，通过试验对比实验者不同步速状态下的测量精度。根据图5 误差精度计算可得，快速和慢速情况下预测平均精度均可达到97% 以上，可完成较为精准的足底压力预测。根据图6、7 分析可得，性别、体重和年龄对预测算法的预测精度没有较大的影响，预测精度都在97.5% 以上，也验证了预测算法的稳定性。

使用预测足底压力数据，可以有效找出步态信息与运动状态的规律，因此建立运动状态和足底压力之间的联系。该运动预测方法可以应用到下肢康复训练和康复医疗器械中，为主动训练运动障碍者提升运动的柔顺性，为康复医疗行业提供运动预测技术和理论支持。