基于双边随机投影算法的光学相干层析成像降噪

潘玲佼，范伟伟，吴全玉

（1.江苏理工学院电气信息工程学院生物信息与医药工程研究所，常州 213001；2.常州大学微电子与控制工程学院，常州 213164）

引 言

光学相干层析成像（Optical coherence tomography，OCT）技术是1991年问世的一种基于低相干干涉的具有高纵向空间分辨率的光学成像技术。它具有非接触性、无创生物组织成像等优势，其最重要的应用之一就是眼科疾病的筛查和诊疗［1］。随着2007年商业化谱域OCT（Spectral⁃domain OCT，SD⁃OCT）技术的问世，实现了三维高分辨率成像，从而进一步推动了OCT 技术在眼科的应用，为青光眼、年龄相关性黄斑变性和糖尿病黄斑水肿等视网膜疾病的定量分析和研究提供了重要帮助［2⁃6］。在SD⁃OCT 中，当OCT 系统对样品组织探测时，将样品组织等效为一系列的反射面，则可探测某深度上组织的反射率，形成A 扫描成像。将光束对组织样品进行横向移动，得出多个A 扫描图像，拼接出一幅二维断层图像，即B 扫描图像。如图1 所示，三维SD⁃OCT 成像由若干二维B 扫描图像组成，每个B 扫描图像又由若干A 扫描组成。OCT 成像系统采用了干涉技术，受低相干光源和成像样本自身结构的共同影响，OCT 图像中含有大量散斑。散斑的相关特性可用来描述微血管系统，反映血流速度等信息，对诊断有一定的价值。然而，由于散斑是多个散射元叠加的结果，在B 扫描图像中表现为大量随机高反差亮斑，这些亮斑称为散斑噪声。散斑噪声淹没了样本的结构细节，导致图像质量退化，严重影响人们对图像信息的准确获取，给医生进行疾病诊断以及计算机辅助疾病诊断分析带来了极大挑战。如何抑制散斑噪声一直是国内外学者致力研究的重要课题。

图1 三维光学相干层析成像示意图Fig.1 Illustration of 3D optical coherence tomography

目前，针对散斑去噪主要有硬件和软件两种处理方法［7⁃9］。硬件方法主要依靠改进光学系统架构，该方法能够有效抑制散斑噪声，但也会使得OCT 成像系统结构更加复杂，造价更高。与硬件方法相比，软件方法无需改变系统结构，更加灵活、易实现。商用OCT 扫描仪提升OCT 成像质量的通用方法是在样本同一位置重复扫描多次，将多次扫描图像叠加取平均来消除散斑噪声。重复扫描图像数量越多，则获得的B 扫描的成像质量越高。然而，随着重复扫描图像数量的增加，相应的扫描时间也会延长。考虑到长时间扫描过程中，眨眼等微小动作都会严重影响成像的质量，因此，需要限制扫描时间。在扫描时间有限的前提下，能完成的扫描次数也是有限的。对同一位置多次重复扫描能有效提高单张B 扫描的成像质量，但会相应减少三维OCT 中B 扫描的数量，从而降低三维成像分辨率。而增加B 扫描的数量又势必降低单张B 扫描的成像质量。本文拟用低秩矩阵理论来解决这一问题。现有的抑制散斑噪声的方法，如空间域局部统计滤波算法［10］、各项异性扩散滤波算法［11］、基于小波变换的滤波算法［12］、基于块匹配的方法［13］等，尽管能在一定程度上有效去除散斑噪声，但并不适合应用在商用OCT 扫描仪上。近年来也有学者尝试用深度学习方法解决散斑问题［14］，然而该方法需要大量图像样本进行训练，且训练时间较长。 王帆等［15］提出了使用主成分分析（Principle component analysis，PCA）方法估计OCT 图像散斑噪声水平。它将OCT 图像原始信号矩阵进行奇异值分解，然后利用一个或几个较大奇异值估计去噪图像。与其他方法相比，该方法仅利用少量相邻帧生物结构的高度相似性，能够在确保去除散斑噪声的同时较好地保留原有生物结构信息。但是这种方法如果对主奇异值选取不当，则会造成散斑噪声估计不准确且鲁棒性较差。袁治灵等［16］提出了一种基于稳健性主成分分析算法（Robust PCA，RPCA）的光学相干层析成像散斑噪声去除方法，将OCT 原始图像分解为散斑噪声图像和样品截面图像的最佳估计之和，一定程度上解决了PCA 方法的缺点。但是该方法只能应用于具有唯一低秩稀疏分解结构的矩阵，并且对于高维数据，求解运算复杂度较高，对于噪声的适应性较差、分解效率低。本文在前人研究基础上，考虑视网膜OCT 成像中眼球运动带来的运动伪差特性，结合双边随机投影算法，提出了一种新的光学层析成像去噪方法。该方法使用双边随机投影代替稳健性主成分分析，降低了计算的时间复杂度，提高了分解速度。通过优化投影可以精确恢复复杂信号，从而准确提取目标信号。

1 基本方法

1.1 算法概述

在三维视网膜OCT 扫描图像中，由于连续扫描的相邻二维图像的生物组织结构信息几乎相同，利用这种组织结构之间高度相似性以及OCT 图像高分辨率特性，可将三维OCT 扫描图像中相邻的若干二维断层图像（即B 扫描图像）中相似的生物组织结构看作一个低秩矩阵。因此，OCT 散斑去噪问题即等同于从被污染的信号中恢复原始低秩矩阵的问题。在视网膜OCT 图像扫描中，信号污染主要来自于两方面，一方面是由于图像扫描过程中人的呼吸、心跳等不可避免因素引起眼球抖动，从而造成了视网膜OCT 图像的运动伪差［17］；另一方面主要来自于扫描中不可避免的散斑噪声。运动伪差信号是少数异常体，相对比较稀疏，具有一定稀疏度，因此可看作是一个稀疏矩阵。而散斑噪声信号则看作是一个噪声矩阵。

图2 给出了算法流程图。首先对OCT 图像进行对齐预处理，增强相邻帧之间的相关性；其次将原始OCT 图像信号分解为无噪低秩矩阵部分、对应运动伪差的稀疏矩阵部分以及噪声矩阵3 部分；最后采用双边随机投影算法求解，提取其中目标信号，从而达到去除噪声、恢复无噪图像的目的。

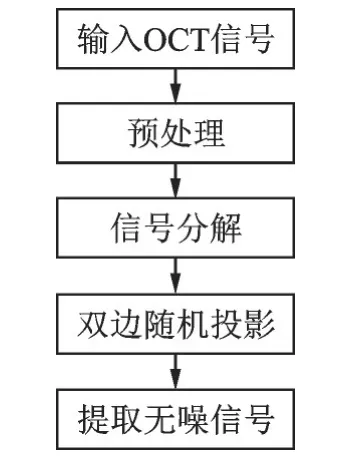
图2 算法流程图Fig.2 Flow chart of the pro⁃posed algorithm

1.2 OCT 图像预处理

如图1 所示，对每个OCT 图像，在慢扫描方向，即Y方向（y⁃z视图），相邻两个B 扫描图像之间存在很大失真，主要表现为相邻两个B 扫描图像跳变。这主要是由于眼睛和头部在垂直方向运动引起的。因此在去噪之前，为保证相邻帧生物组织结构之间的高度相似性，首先需进行对齐处理，从而保证信号提取的准确性。

B 扫描图像对齐步骤如下。首先分割出OCT 图像中视网膜上边界，因为该边界在视网膜所有边界中最为突出，比较容易准确地进行分割，本文采用多分辨率表面检测方法［18］进行分割。分割后计算B扫描图像中视网膜上边界的平均深度。假设M×N大小的第j帧B 扫描图像分割后视网膜上边界各像素点的深度分别为dij（i=0，1，2，…，N-1），则第j帧B 扫描图像视网膜上边界的平均深度为

由于视网膜上边界中心凹是自然凹的曲面，因此，式（1）只使用除中心凹外左侧和右侧各t个像素点，t≈0.2N。以最小作为基准dbase，则各B 扫描图像的位移值为

各B 扫描图像根据Δdj纵向位移进行对齐，对齐后所有B 扫描图像视网膜上边界的平均深度一致。

视网膜上表面校正前后效果如图3 所示。对齐之前相邻B 扫描之间有很多跳变，视网膜上表面高低起伏。对齐之后相邻B 扫描之间平滑连续，视网膜上表面也趋于平滑。对齐之后大大减少了运动伪差的影响，视网膜各层趋于平滑，视网膜成像形状更为逼真。

图3 OCT 图像预处理前后的三维渲染图Fig.3 3D rendering of the OCT image before and after preprocessing

1.3 OCT 信号分解

根据低秩分解理论，退化图像矩阵X可分解为低秩矩阵L、稀疏矩阵S和噪声矩阵N之和，退化前的数据可通过低秩矩阵来逼近。

在三维视网膜OCT 扫描图像中，由于连续扫描的相邻二维图像的生物组织结构信息几乎相同，若将一帧包含m个像素的二维扫描图像看作矩阵列向量，相邻n帧二维扫描图像中相似的生物组织结构则可看作低秩矩阵，而该n帧图像中的运动伪差和噪声可分别看作稀疏矩阵和噪声矩阵。OCT 设备采集的相邻n帧数据则可看作退化图像矩阵。本文取n为5 以保证生物组织结构的相似度，其矩阵关系式为

抑制OCT 图像噪声即要使N能量最小，即

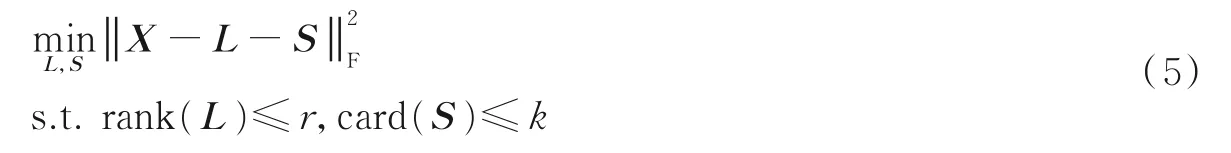
式中：‖ ⋅‖F为Frobenius 范数，rank 为矩阵秩，card 为矩阵分量个数。由于式（5）中L和S均为未知矩阵，给定r和k，式（5）的优化问题可转化为以下两个交替求解直至收敛的子问题，即

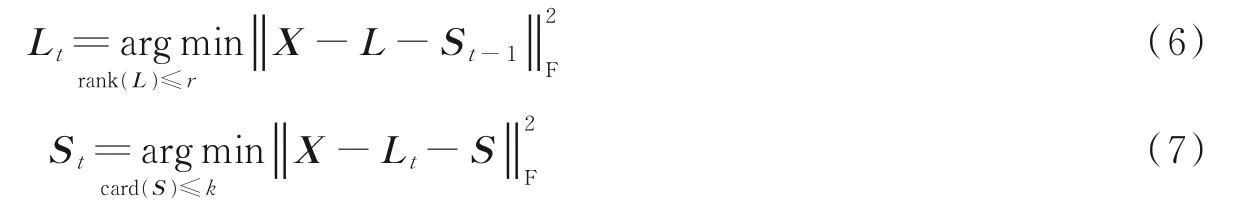
式中：Lt和St分别为t次迭代后的低秩部分和稀疏部分。

1.4 双边随机投影散斑去噪

尽管奇异值分解的低秩逼近能够达到对原始数据的最小重构误差，但这一方法用于三维OCT 图像这样的高维数据计算复杂度较高。本文采用了双边随机投影低秩逼近方法来近似和加速奇异值分解低秩逼近。根据双边随机投影算法［19］，若有矩阵X∈Rm×n(m>n) 的双边随机投影Y1=XA1和Y2=XTA2，A1∈Rm×r，A2∈Rn×r均为高斯随机矩阵，则可构造X的r秩低秩矩阵L，即

为进一步提升低秩逼近的精度，使用power scheme 模型［20］进行优化。用矩阵=(XXT)q X替代X计算双边随机投影。因为与X相比，的奇异值衰减更快，且X与的奇异向量相同。的双边随机投影为

为进一步优化低秩逼近的速度和精度，对Y1和Y2进行矩阵正交三角分解（QR 分解），即

则X的r秩快速低秩逼近可改写成

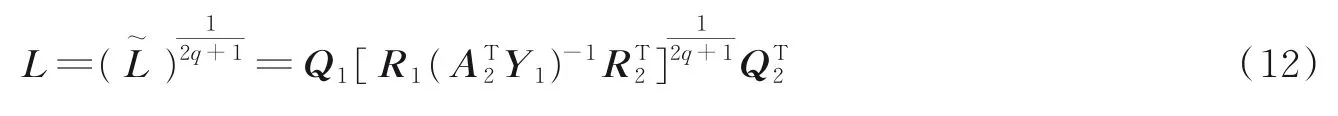
在实际操作中，常使用右投影矩阵Y1和左投影矩阵Y2来更新A1和A2，以有效提高低秩逼近的精度。式（7）中St取决于X-Lt的硬阈值，即

式中：℘k(X-Lt)为矩阵元硬阈值算子，该算子保留|X- |Lt中最大的k个元素，而将其他元素置0。

综上，双边随机投影散斑去噪算法的求解步骤如下：

（1）输入观测到的OCT 数据X，设置参数q，tmax；

（2）初始化稀疏矩阵S、低秩矩阵L及高斯随机矩阵A1，令L=X，S=0；

（4）计算右随机投影矩阵Y1=L^A1，更新A2=Y1，计算左随机投影矩阵A2（式（9））；

（5）更新A1，使得A1=Y2，若循环次数未达到q+ 1 次，则循环更新Y1和Y2，否则进行下一步；

（6）对Y1和Y2进行QR 分解（式（11）），求解Lt（式（12））；

（7）求解St（式（13））；

2 实验结果与分析

实验对象为10 名正常男性青年和5 名正常女性青年，对其以黄斑为中心的视网膜OCT 图像数据进行测试。视网膜OCT 图像均使用Topcon DRI OCT⁃1 扫描获得；图像大小为512 体素×992 体素×256 体素，覆盖了以黄斑为中心的6 mm×6 mm×2.5 mm 区域。

2.1 图像质量评价标准

为有效评价本文所提出方法的有效性，引入了常用的3 个图像质量评价指标，分别为信噪比（Sig⁃nal to noise ratio，SNR）、对比度信噪比（Contrast to noise ratio，CNR）以及等效视数（Equivalent number of looks，ENL），其计算公式分别为

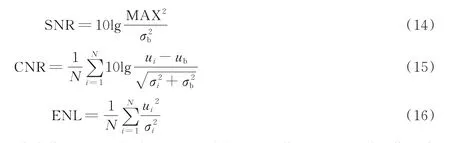
式中：MAX 为B 扫描图像的最大可能像素值；σb和ub分别为背景区域方差和均值；σi和ui分别为若干感兴趣区域的方差和均值；N为感兴趣区域个数。SNR 值越高则代表OCT 图像背景区域的图像质量越好；CNR 反映了两种组织信号强度的相对差别，主要用来衡量图像前景和背景的对比度，数值越大则图像的对比度越好；ENL 主要用来评价图像光滑度和反映信号强度，与CNR 相似，ENL 通常选取若干感兴趣区域进行评价。本文实验在视网膜图像神经纤维层、内视网膜以及视网膜色素上皮层上随机选取了3 个区域作为感兴趣区域。

2.2 仿真结果与分析

用本文所提的双边随机投影去噪方法对临床数据集进行测试，实验结果如图4 所示。在原始图像和去噪图像中选取对应位置的A 扫描图像（图4 中黄线位置）分别绘制一维深度信息信号图（图5）。随着深度逐渐增大，视网膜从上而下对应的结构组织分别为神经纤维层（Retinal nerve fiber layer，RN⁃FL）、神经节细胞层（Ganglion cell layer，GCL）、内 从状层（Inner plexiform layer，IPL）、内核层（Inner nuclear layer，INL）、外从状层（Outer plexiform layer，OPL）、外核层（Outer nuclear layer，ONL）、内节/外节（Inner segments layer/ outer segments layer，IS/OS）、视网膜色素上皮层（Retinal pig⁃ment epithelium，RPE）以及脉络膜（Cho⁃roid）等。对比图5 中去噪处理前后的深度信息信号图可见，去噪处理后信号曲线的光滑度以及视网膜生物结构信息对比度都有明显提升。

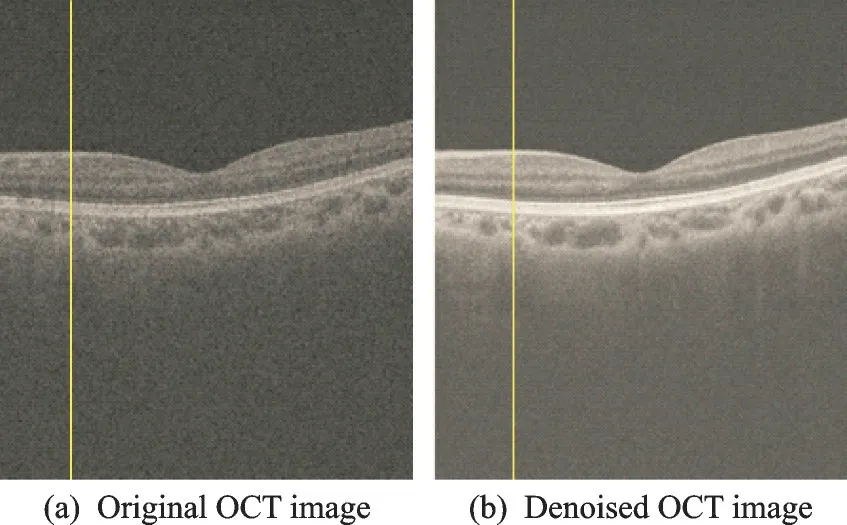
图4 双边随机投影去噪实验结果Fig.4 Experimental result of bilateral random projection denoising

图5 一维深度信息信号图Fig.5 One⁃dimensional depth information signal map

为更好地评价本文方法客观性能，将原始图像与本文提出的双边随机投影去噪方法以及RPCA 算法［16］进行对比分析。 图6为不同去噪方法处理所得的去噪效果对比图。原始图像以及各算法处理得到的去噪图像的量化分析结果如表1 所示。

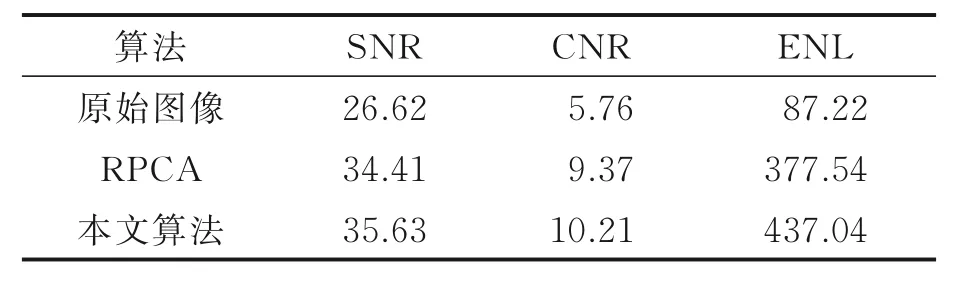
表1 各算法去噪结果Table 1 Denoising results of different algorithms

由图6 可知，采用双边随机投影去噪方法处理的图像整体更加光滑、对比度更高、图像质量更好。与RPCA 算法相比，本文方法在信噪比、对比度信噪比以及等效视数指标上分别提高了1.22 dB、0.84 dB 和59.5，去噪效果更好。这些指标的提高也意味着临床医生看到的OCT图像中信号强度更强，视网膜各组织结构间对比度更好，各组织结构边界更加平滑，图像的可读性更好。这将有利于提升医生的阅片速度和阅片质量，同时也能有效提升计算机辅助诊断分析，如视网膜自动分层，病变区域自动分割等的精度。除此之外，本文对各方法的计算复杂度也进行了评估。 在Intel（R）Core（TM）2 Duo CPU 处理器和8 GB RAM 的PC 机，MATLAB 2017a 软件上进行了测试，用RPCA 算法和本文算法对实验数据集中单幅B扫描图像的处理时间分别为4 s 和0.3 s。本文算法大大降低了计算复杂度。

图6 各算法去噪结果Fig.6 Denoising results of different algorithms

为进一步说明本文方法的临床价值，对10 名临床早期青光眼患者的OCT 图像进行了分割，并评估了散斑去噪对分割精度的影响。青光眼诊断的指标之一是神经节细胞层加上内丛状层（GCL+IPL）以及神经节细胞复合层（RNFL+GCL+IPL，GCC）的厚度。人工对三维视网膜OCT 图像进行分层测量费时费力，因此，眼科医生需要一种可靠高效的方法来定量分析视网膜结构参数。为了评价散斑去噪处理对提升青光眼诊断精度和效率的作用，将去噪前后图像分割的结果与分层金标准进行比较。金标准由两名专业眼科医生独立手工标注，标注结果取平均值作为参考基准。由于三维OCT 图像数据量很大，因此在标注时每个三维OCT 图像中仅选取16 个B 扫描图像进行标注。OCT 原始图像，去噪后图像均采用爱荷华大学提供的可视化软件OCT⁃Explorer 进行自动层分割［21］。将分割结果与参考基准进行比较，计算层表面边界定位误差的均值，结果如表2 所示。结果表明，经本文算法去除散斑噪声后，分割精度得到了提升。本文方法去噪后的图像边界定位误差均值最小、分割精度最高，有助于医生进行精准化的计算机辅助疾病诊断及分析。

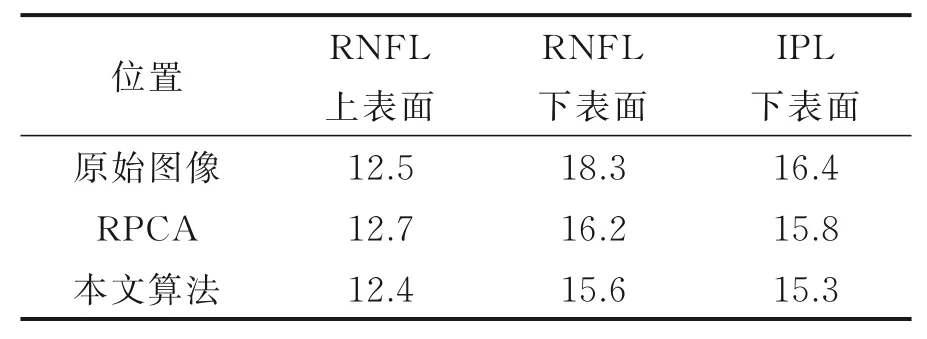
表2 早期青光眼分割无符号表面误差比较Table 2 Comparison of unsigned surface error in early glaucoma layer segmentation μm

3 结束语

针对含有噪声的视网膜OCT 图像，首先进行预处理，减少眼动伪差，从而保证相邻帧生物组织结构之间的高度相似性；随后，利用相邻帧生物组织结构之间高度相似性及图像高分辨率特性对原始OCT 图像信号进行分解，将其分解为无噪低秩矩阵、稀疏矩阵以及噪声矩阵；最后，采用双边随机投影算法求解无噪低秩矩阵，从而达到去除散斑噪声的目的。该方法的主要优势在于不需要大量训练数据，利用少量相邻帧即可在去除散斑的同时保留原有生物结构信息，运算效率较高。实验结果表明，基于双边随机投影的去噪算法能有效地抑制视网膜OCT 影像中的散斑噪声，获得了较好的视觉效果，且计算复杂度较低。除了应用在OCT 图像去噪外，该方法还适用于高光谱影像去噪［22］、脑电信号提取［23］、雷达信号分析［24］和目标检测等领域［25］，有广泛的应用前景。该方法的提出为医生进行视网膜疾病诊断以及改善计算机自动辅助视网膜疾病分析的性能提供了有效帮助，且计算时间可以满足临床的实时性要求。然而，对于病变视网膜，由于视网膜结构发生严重形变，相邻帧的结构相关性也相应减少，从而影响算法精度，因此，在下一步研究工作中将重点考虑如何改进本方法使之适用于严重病变视网膜的去噪。