基于互相关函数的聚类蝴蝶优化算法的结构损伤识别
2021-09-19周宏元张广才王小娟陈凤晨倪萍禾
周宏元, 张广才, 王小娟, 陈凤晨, 倪萍禾
(1.北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124;2.中国民航机场建设集团有限公司,北京 100101)
土木工程结构在长期服役过程中易受到超载、环境侵蚀、材料老化、疲劳破坏等不利因素影响,不可避免地出现损伤破坏,造成结构承载力降低,如未被及时发现,损伤逐渐累积可能导致结构整体坍塌,引发灾难性后果。因此,为保证结构安全识别,判断结构是否发生损伤,并确定损伤位置和程度,大量基于频域和时域的损伤识别方法被提出[1]。其中,频域方法通过频率、模态振型、模态应变能等模态参数进行损伤识别[2-4],但低阶模态对小损伤不敏感,而高阶模态信息虽对小损伤更加敏感却难以准确获取,限制了频域方法在实际工程中的应用[5]。对于时域方法,如基于灵敏度的损伤检测方法[6],自适应扩展卡尔曼滤波[7],自适应二次和平方误差法[8]等,直接利用传感器测得的结构响应(位移、速度、加速度)识别损伤,比频域方法更加简单高效。
上述方法一般都需要施加外激励,但在桥梁、海上平台、大跨空间结构等大型工程结构上难以施加所需激励,且在结构上施加大量激励能量可能导致结构局部损坏。对比人工激励的方法,利用环境随机激励(风荷载、交通荷载、波浪荷载等)下结构的响应识别损伤更符合工程结构的实际工作状态,成本低且易于操作,更具研究价值和应用前景。于哲峰等[9]提出基于互相关函数幅度矢量CorV的结构损伤识别方法,利用损伤前后CorV变化来检测和定位损伤。在此基础上,雷家艳等[10]利用随机激励下相邻测点动力响应的互相关函数识别结构损伤,并通过八层剪切型钢框架的振动试验验证了该方法的有效性。Li等[11]提出加速度响应互相关函数协方差的协方差矩阵,并发现该矩阵比频率和模态振型对局部损伤更敏感。进一步,Ni等[12]提出多点未知随机激励下基于互相关函数的结构损伤识别方法,而且不要求传感器数量多于激励数,能够使用较少测点识别大型结构。
传统优化方法往往需要较好的初始值和梯度信息,否则很难保证识别结果的准确性,而基于种群的智能优化算法全局搜索能力更强,限制条件少且易于并行计算,近年来受到了广泛的关注。遗传算法、粒子群优化算法、人工蜂群算法、蚁狮优化算法等已被应用到结构损伤识别中并取得了较好的效果[13-16]。蝴蝶优化算法[17](butterfly optimization algorithms,BOA)是近年提出的启发式群智能优化算法,它主要基于蝴蝶利用嗅觉确定食物位置和交配对象的策略,模拟蝴蝶觅食和交配行为。该算法设计参数少,概念简单且易于实施,收敛速度快,已经成功应用于无线传感器节点定位[18]和约束条件下三个经典工程设计问题[19],但尚未应用于结构损伤识别领域。研究发现蝴蝶优化算法存在全局搜索能力差,有时陷入局部最优等问题[20]。为改进BOA,提出在蝴蝶个体更新迭代前引入k均值聚类得到聚类蝴蝶优化算法(clustering butterfly optimization algorithm,CBOA),k均值聚类可以更充分的利用种群信息,平衡全局搜索和局部搜索的关系以增强算法的性能。
本文提出多点随机激励下基于加速度响应互相关函数的损伤识别方法,分别采用BOA和CBOA进行损伤识别,然后通过简支梁和剪切型钢框架结构进行数值验证,并考虑了噪声对识别结果的影响。识别结果表明,相较于BOA,CBOA能够更加准确识别损伤位置和程度,并且表现出更优的搜索能力和噪声鲁棒性。
1 加速度响应互相关函数
多点输入外激励下多自由度线性结构的运动方程为
(1)
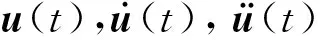
假定结构的初始速度和位移为0,结构所受随机激励F(t)为白噪声,对于线性结构体系,外激励时程可视作一系列连续短脉冲的组合,因此结构中任意第μ处的加速度响应可用积分形式表示为
(2)

(3)
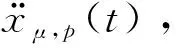
(4)
式中,nf为外激励数。
(5)
进一步可得

E(Fp(μ1)Fq(μ2))dμ1dμ2
(6)
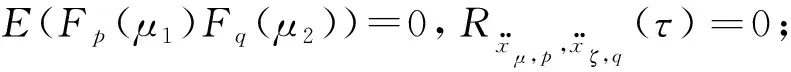
E(Fp(μ1)Fp(μ2))=Spδ(μ1-μ2)
(7)
式中:常数Sp为外激励功率谱密度;δ(μ1-μ2)是狄拉克函数(Dirac delta function)

(8)
(9)
另一部分是与结构参数无关,与外激励有关的功率谱密度Sp,所以式(8)中互相关函数可继续简化为
[S1,S2,…,Sp…,Snf]T
(10)
其中单元脉冲响应H取决于刚度和质量等结构参数θ
H(θ)=[H1,H2,…,Hp,…,Hnf]
(11)
与外激励能量有关的部分可表示为以下向量形式
S=[S1,S2,…,Sp,…,Snf]T
(12)
因此互相关函数表示如下
(13)
2 结构损伤识别问题
目前研究普遍采用折减弹性模量,忽略质量变化模拟结构的损伤,但实际上结构的损伤可能伴随着质量和刚度的同时减少,如混凝土发生局部脱落,钢材发生局部锈蚀使密度和截面积减小等,这种情况下,引入损伤因子向量α=(α1,α2,…,αe,…,αn)和β=(β1,β2,…,βe,…,βn)同时考虑了刚度和质量的改变,可以更加准确的模拟结构损伤模式。损伤后结构的整体刚度矩阵Kd和质量矩阵Md可分别由式(14)和(15)表示为
(14)
(15)
式中:n为结构划分的总单元数;Ke,ele和Me,ele表示第e个单元刚度矩阵和质量矩阵;αe和βe代表第e个单元的刚度和质量损伤程度,αe=0和βe=0分别表示第e个单元无刚度和质量损伤,αe=1和βe=1表示第e个单元刚度和质量完全损伤,所以结构损伤识别问题可转化为识别损伤因子向量α和β。

实际上,测量互相关函数Rmea可以由测量的加速度和参考点直接计算得到,但未知环境激励下,式(12)中的与外激励能量有关的向量S不能直接计算得到,只能先用下式逆运算间接计算Scal
(16)
式中:计算单元脉冲响应Hcal是结构参数θ的函数,可以利用式(3)计算单位脉冲响应函数,然后通过式(9)和(11)计算得到Hcal。
已知Hcal和Scal后,可由式(13)得到计算互相关函数Rcal。测量互相关函数Rmea和计算互相关函数Rcal之间的差值越小,则结构损伤的识别结果越接近真实值,即使用优化算法识别损伤的核心思想如下式,使两者差值尽可能小
minRmea-Rcal
(17)
3 优化算法
3.1 蝴蝶优化算法
BOA是近年提出的一种启发式群智能优化算法, 主要模拟蝴蝶的觅食和交配行为,其核心策略在于蝴蝶利用嗅觉确定花蜜位置和交配对象。每一只蝴蝶代表一种可能解,当蝴蝶根据气味从一个位置移动到另一个位置时会生成新的解。该算法存在三个理想化条件:① 所有的蝴蝶都会散发出某种香味,使蝴蝶互相吸引;② 蝴蝶感受到的香味强度由其计算出的适应性函数决定;③ 每只蝴蝶都可以随机移动,或朝着散发出最多香味的蝴蝶位置移动。
BOA作为一种基于种群的智能优化算法,生成初始蝴蝶种群的方法如下
Xid=Xid,l+rid×(Xid,u-Xid,l)
(18)
式中:Xid,u和Xid,l表示搜索域的上下限;rid是[0, 1]之间的随机数;i和d分别表示种群第i只蝴蝶和变量个数。
由该算法的理想化条件可知,蝴蝶可以感知到某种与其适应性相关的香味,即当蝴蝶从一个位置移动到另一个位置时,感知到的香味信息会随着其适应性函数发生变化,其具体表达式如下
IFi=CIA
(19)
式中:IFi是第i只蝴蝶感知到的香味信息(fragrance information,FI);I是香味刺激强度,由适应性函数fitness决定;C是感觉形态,对算法的收敛速度有很大影响;A是幂指数,它影响香味的感知程度,A=1表示香味信息没有在传播中丢失,可以被全部感知,A=0表示香味信息在传播过程中全部丢失,不能被蝴蝶感知。
BOA包括全局搜索和局部搜索两种生成子代的方式,可分别由式(20)和式(21)表示为
(20)
(21)
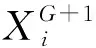
BOA另一个重要的参数是转换概率(switch probability,SP),它决定着执行全局搜索或局部搜索,SP取值范围为[0, 1]。对于每一蝴蝶个体判断是否r>SP,其中r为[0,1]之间的随机数,如果r>SP,则蝴蝶会随机移动,即利用式(20)执行全局搜索,否则蝴蝶朝着最优蝴蝶位置移动,即利用式(21)执行局部搜索阶段。
3.2 聚类蝴蝶优化算法
虽然BOA在标准函数测试中相比于遗传算法、差分进化算法、粒子群算法等展现出更优的结果,表现了较强的搜索能力,但BOA简单的变异机制使其面临着收敛速度慢,有时陷入局部最优等问题。为改进BOA,平衡全局搜索和局部搜索能力,本文提出聚类蝴蝶优化算法(CBOA)。
聚类技术是机器学习领域中的重要研究内容之一,其中k均值聚类因简单,高效的特点被广泛研究和使用,它可以发现数据的内在结构并根据其特征划分为若干类,使得各个类内的数据相对于不同类之间的数据更为相似,每个聚类中心就可以代表该类中所有数据信息。因此,引入聚类技术可以更加有效的利用种群信息,增加BOA的收敛速度,k均值聚类具体实现步骤如下:

步骤2使用欧式距离计算种群中各样本Xm与各个聚类中心Cj的距离D。
(22)
式中,d表示样本的维度,即未知数的个数。

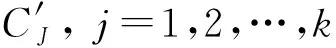
(23)
式中:nj表示归于聚类中心Cj的样本数目;Xj是归于聚类中心Cj的样本。
步骤5从当前种群P再随机选择k个样本组成集合B,结合步骤4中新的聚类中心得到集合B′,然后计算集合B′中每个样本的目标函数值并对其从小到大排列,最后选择值较小的前k个样本放入种群P替换集合B中的样本,精英个体被保留。
BOA引入k均值聚类后得到CBOA,在种群个体更新迭代前执行k均值聚类操作,结构清晰易于实施。本文提出的多点未知随机激励下,基于互相关函数的CBOA的结构损伤识别方法,如图1所示,虚线是CBOA算法,具体实施步骤如下。

图1 基于CBOA损伤识别流程图Fig.1 The flowchart of damage identification based on CBOA
(1) 设置刚度,质量损伤程度,即损伤因子向量α和β,然后得到损伤后结构参数θ;
(2) 多点白噪声激励下,测量损伤后结构的加速度响应,指定参考点,然后直接得到加速度响应互相关函数Rmea;
(3) 初始化聚类蝴蝶优化算法参数,并在搜索域[0, 1]内随机生成初始结构参数θ*;

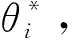
(24)
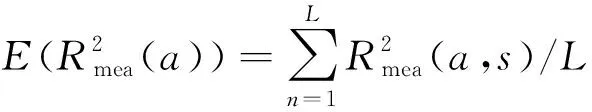
(6) 重复执行(4)和(5)直到达到最大跌迭代次数或满足以下收敛条件:
(25)
式中:errorG表示第G次迭代时识别的结构参数误差;Tol表示收敛条件;
(7) 如果满足(6)中的终止条件,则输出最优结构参数解。
4 数值模拟
为测试本文提出的识别方法的有效性,分别采用10单元简支梁和10层剪切型钢框架作为数值算例。BOA和CBOA的参数设置为:感觉形态C=2,幂指数A=0.1,转换概率SP=0.8,初始种群规模为60,最大迭代次数设置为200,收敛条件Tol=10-2,取10次计算结果的平均值以保证其准确性。
4.1 简支梁
简支梁模型如图2所示,跨度为1 000 mm,截面高和宽分别为6 mm和50 mm,共11个节点划分为10个单元,每个单元长100 mm。每个中间节点有两个自由度,即垂直平移和旋转,而两个支撑节点只考虑旋转。该简支梁材料为钢材,弹性模量E=2.1×1011N/m2, 密度为ρ=7 860 kg/m3。均值为0标准差为1的未知随机荷载垂直作用在节点2、4、6、8、10,3个加速度计安装在节点3、5、7以获得垂直方向的加速度响应,采样频率为2 000 Hz,总记录时长为1 800 s。
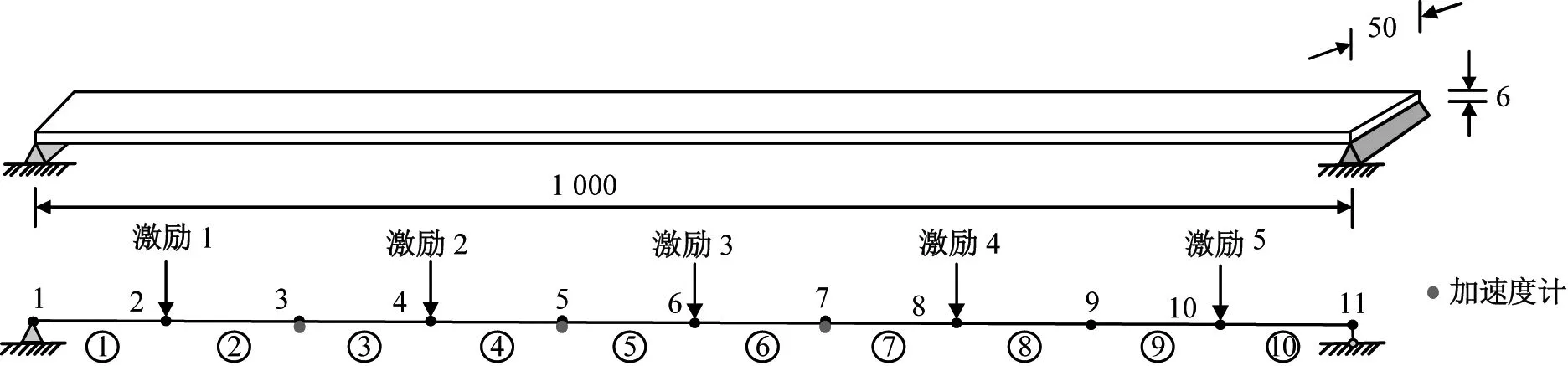
图2 简支梁模型(mm)Fig.2 Numerical model of the simply supported beam(mm)
Wang等[22]研究发现,参考点的选择不会明显影响识别结果,本算例选取节点7测量的加速度数据作为参考,可以得到3组自/互相关函数数据R3,7、R5,7、R7,7,识别质量和刚度损伤。

(26)
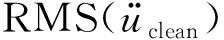
图3展示了无噪声时使用BOA和CBOA得到的目标函数收敛曲线,可以明显观察到CBOA收敛速度更快,且只需要迭代109次提前满足收敛条件而中止,但BOA经过200次迭代仍未收敛,可以看出,CBOA收敛速度更快,搜索能力更强。
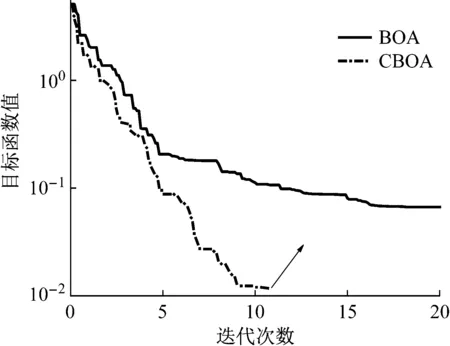
图3 BOA和CBOA的迭代收敛图Fig.3 Convergence process of objective function
图4和图5分别为无噪声和20%噪声情况下简支梁的刚度和质量损伤识别结果,表1统计了识别结果的平均误差和最大误差。无噪声时,BOA和CBOA都可以精确地识别出单元4和单元6发生的损伤程度,但CBOA几乎没有出现错误识别,而BOA在单元1,单元3,单元9存在较明显的识别误差,最大识别误差为4.90%。当测量的响应被20%的白噪声污染时,刚度和质量损伤的最大识别误差分别为6.82%和6.19%,考虑到多个未知荷载以及有限的传感器测量数据,BOA的识别结果是可以接受的,而CBOA对于刚度和质量损伤的最大识别误差仅为1.56%和2.34%,这说明聚类技术有效的增强了BOA的搜索能力,有助于更加准确识别结构的损伤。
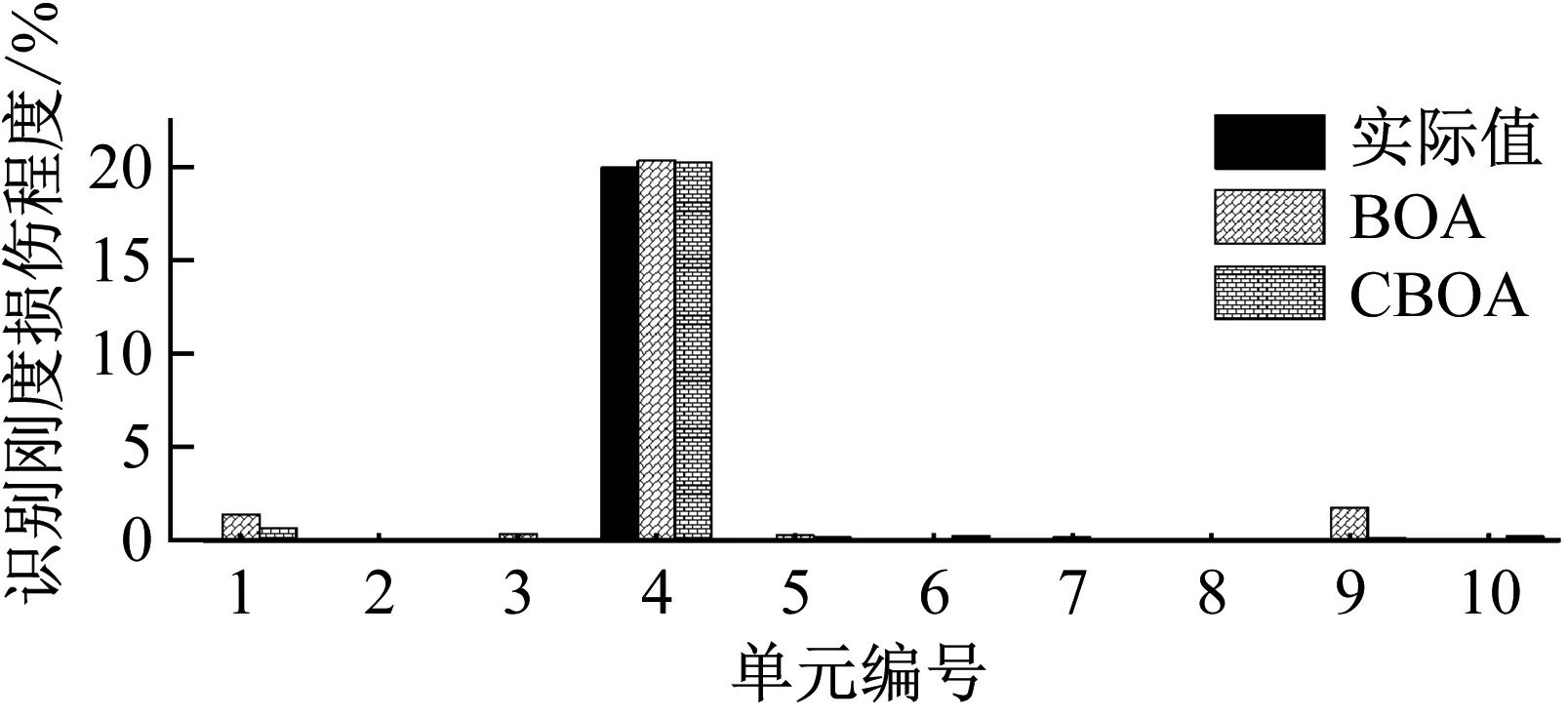
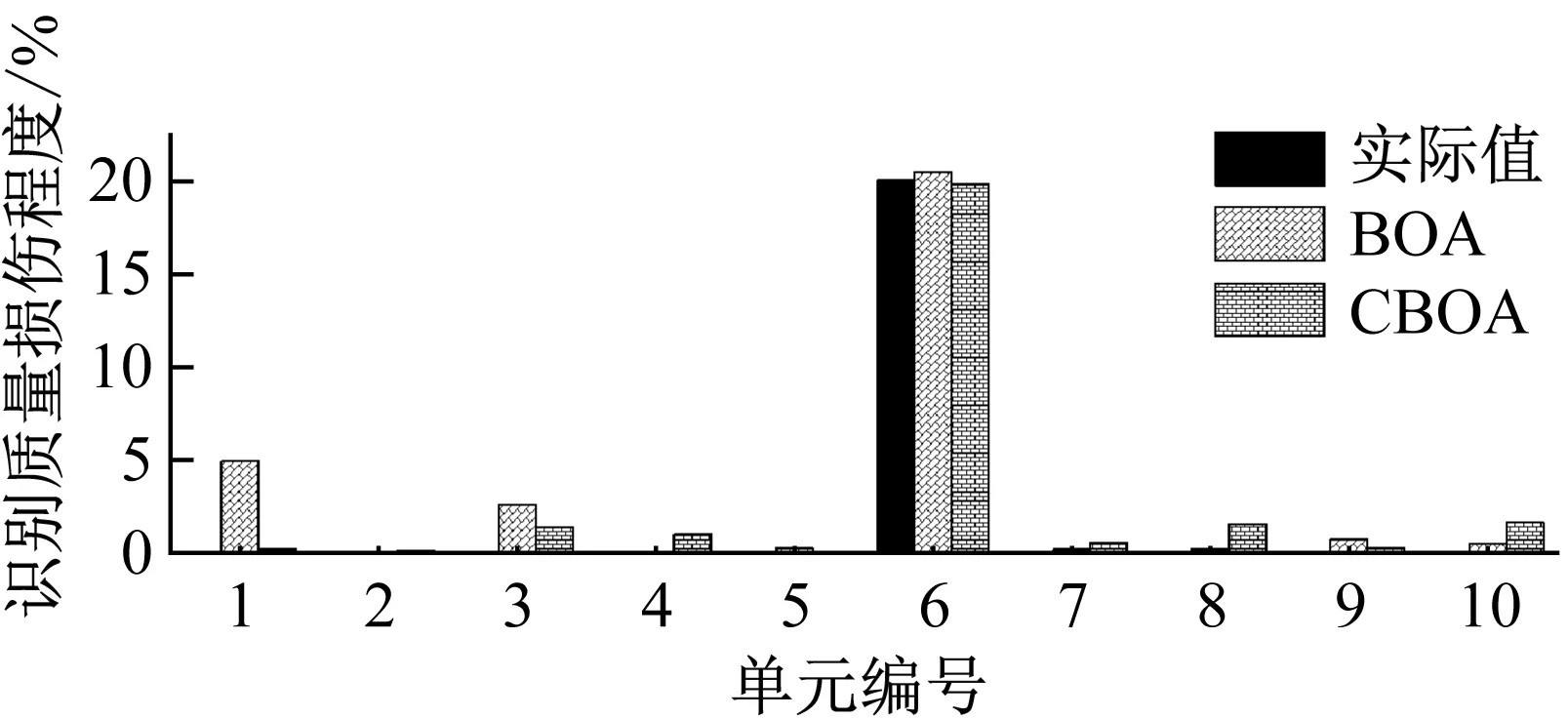
图4 无噪声条件下简支梁损伤识别结果Fig.4 Identification results of simply supported beam without noise


图5 20%噪声下简支梁损伤识别结果Fig.5 Identification results of simply supported beam with 20% noise

表1 简支梁刚度和质量识别误差Tab.1 Identification errors for the simply supported beam %
对此图4和图5可以发现,20%的噪声没有明显影响识别结果,这说明基于互相关函数的蝴蝶优化算法对噪声具有较好的鲁棒性,其内在原因由图6所示,通过对比有无噪声时互相关函数值,可以观察到添加20%的噪声至加速度测量值后,R5,7和无噪声时该互相关函数基本重合,具体关系可由相对误差ER(relative error,RE)和皮尔森相关系数(COR)量化
(27)
(28)
式中:Rn0为无噪声时R5,7,Rn20表示添加20%的噪声时R5,7;COV为协方差;σ为标准差。

图6 互相关函数R5,7有无噪声对比图Fig.6 Comparison between the correlation function R5,7 with and without noise
利用式(27)和(28)计算结果分别为ER=1.3%,COR=0.999 8, 此结果表明无噪声条件下互相关函数R5,7值变化很小,因此本文提出的方法对噪声不敏感。
4.2 剪切型钢框架
图7为10层钢框架模型,高2 500 mm,宽600 mm;每层钢梁宽度和厚度分别为100 mm和25 mm,钢柱截面尺寸为50 mm×5 mm。弹性模量E=2.1×1011N/m2, 密度为ρ=7 850 kg/m3。钢框架底部边界条件为固支,钢柱与钢梁刚接,且由于钢框架的质量只要集中在钢梁,所以可以简化为图7(b)的10层剪切型集中质量块模型。均值为0,标准差为1的未知随机荷载沿X方向施加在每一层,4个加速度计分别安装在1、3、6、9层采集X方向的加速度响应,采样频率为1 000 Hz,总记录时长为1 800 s。选取第6层测量的加速度数据作为参考,然后得到4组自/互相关函数数据R1,6、R3,6、R6,6、R9,6,识别质量和刚度损伤。

图7 十层钢框架(mm)Fig.7 Ten-floor steel frame (mm)
实际上结构可能发生多处损伤,或者某一单元同时发生刚度和质量的损伤,因此假定单元2、单元4和单元8分别发生30%、20%和10%的刚度损伤,同时单元4发生20%的质量损伤,即α2=0.3,α4=0.2,α8=0.1,β2= 0.2。为研究噪声对算法的影响,20%的高斯白噪声添加到测量数据。
图8和图9分别为无噪声和20%噪声下钢框架的刚度和质量损伤识别结果,表2统计了识别结果的平均误差和最大误差。无噪声时,BOA对于刚度和质量损伤的最大识别误差分别为2.92%和3.84%,CBOA对于刚度和质量损伤的最大识别误差分别为1.88%和2.13%,因此BOA和CBOA不仅可以成功定位损伤单元的位置,还可以较为准确识别损伤程度。当测量的响应被20%的白噪声污染时,BOA的识别误差明显增大,刚度和质量损伤的最大识别误差分别为8.05%和8.21%,多处识别误差超过5%,然而,CBOA仍然可以准确的识别单元损伤位置和程度,刚度和质量损伤的最大识别误差仅为2.85%和3.55%。与BOA相比,CBOA对噪声更加的不敏感,可以更加精确识别多处损伤以及质量和刚度发生同时损伤情况。

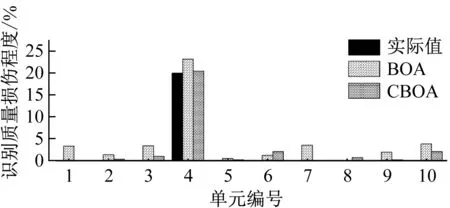
图8 无噪声条件下钢框架的损伤识别结果Fig.8 Identification results of the steel frame without noise


图9 20%噪声下钢框架的损伤识别结果Fig.9 Identification results of the steel frame with 20% noise

表2 钢框架刚度和质量识别误差Tab.2 Identification errors for the steel frame %
5 结 论
蝴蝶优化算法是近年新提出的一种启发式智能算法,但该算法存在收敛速度慢,有时陷入局部最优的问题,为提高其性能,本文将k均值聚类算法引入到蝴蝶优化算法,提出了基于互相关函数的聚类蝴蝶优化算法的结构损伤识别方法,识别多点未知随机激励下结构的刚度和质量损伤。通过简支梁和剪切型钢框架两个数值模拟算例,验证了所提出方法的可行性和有效性,并得到以下结论:
(1) 相比于比蝴蝶优化算法,本文提出的聚类蝴蝶优化算法有更强的优化能力,表现出更快的收敛速度,20%的高斯白噪声污染下,基于互相关函数的聚类蝴蝶优化算法仍能精确识别结构的多处损伤以及质量和刚度的同时损伤,且几乎没有错误识别。
(2) 鉴于该方法使用时域内有限测点的不完备数据,并考虑噪声等不确定因素的影响,不需要复杂的数据后处理,利用未知环境激励下采集到的结构振动响应数据识别结构损伤,而且不要求传感器数量多于激励的荷载数,因此可以使用较少的传感器监测大型结构的健康状况,对于实时结构健康监测具有一定的指导意义。
