海底地震动对近海桥梁易损性影响

王德斌， 李 新， 孙治国， 王东升， 陈宝魁

(1.大连交通大学 土木工程学院，辽宁 大连 116028； 2.防灾科技学院 土木工程学院，北京 101601；3.河北工业大学 土木与交通学院，天津 300401； 4.南昌大学 建筑工程学院，南昌 330031)

易损性方法因其能够量化工程结构各项抗震指标，直观、高效的反映结构的抗震能力，近年来被广泛应用于桥梁抗震性能分析中。针对近海桥梁结构，国内外学者利用易损性方法进行了许多相关研究[1-4]。但由于在实测地震动数据中，关于海底地震动的内容十分有限，因此绝大多数针对近海桥梁抗震性能的研究中，研究人员往往以陆地地震动代替海底地震动开展。

根据Boore等[5]的研究，海水层不仅影响到地震动的传导，而且会显著增强其场地放大效应，从而造成海底地震动与陆地地震动之间的显著差异。Li等[6]根据一维波传播理论、流体动力学方程，采用谱表示法模拟了海底表面地震动，发现海底地震动水平向放大效应较陆地地震动更为显著。周越等[7]基于小波变换的方法对美国加州及日本近海海域地震动加速度记录进行小波包分解，发现近海海底地震动相较于陆地地震动，能量主要分布于低频带，并表现出能量分布的宽频带特性。Chen等[8]基于日本K-net和美国SEMS地震记录，对比了近海和陆地地震动的差异，发现水平向近海地震动记录标准反应谱的平台段更宽，且特征周期偏大。由此可认为，基于陆地地震动获得的近海桥梁结构抗震性能的研究成果并不十分准确。

近海桥梁在服役年限内，极有可能会受到海底地震动的影响，进行关于海底地震动对近海桥梁易损性的研究是把握其抗震能力的必要手段。遗憾的是，由于目前可用的近海海域地震动记录有限，导致目前开展的考虑海底地震动影响的近海桥梁抗震性能的研究极少。

本文采用ABAQUS有限元软件建立某近海多跨连续梁桥有限元模型，基于一维波传播理论、流体动力学基本方程，并利用谱表示法模拟海底表面的三向平动地震动，以海底、陆地地震动作为变量分两种工况对多跨连续梁桥进行非线性动力时程分析，并基于此建立桥墩的易损性曲线，针对海底地震动对近海桥梁结构易损性的影响进行深入研究。

1 桥梁结构有限元分析模型

1.1 桥梁概况

本文以某跨海大桥引桥段为例，图1为桥梁结构简图及各截面尺寸图。本桥为等跨径六跨连续梁桥，单跨长110 m，总桥长660 m。其中1#墩、7#墩为过渡墩，2#、6#墩为次边墩，3#墩、4#墩、5#墩为中墩。除主梁为采用Q345级钢的钢梁外，桥墩、系梁、承台均为钢筋混凝土结构。其中，桥墩及系梁采用C50混凝土，承台为C45混凝土。主梁与墩身之间采用三种铅芯橡胶支座，各支座具体参数如表1所示。桥梁结构所处场区抗震设防烈度为8度，设计服役年限为120年。

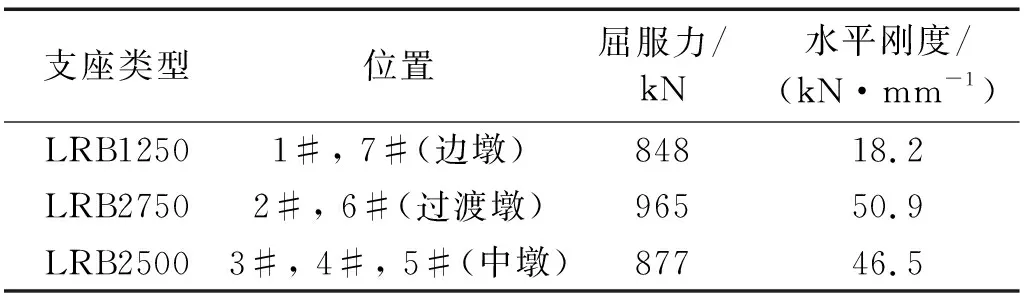
表1 桥梁部件材料Tab.1 Bridge component material

1.2 有限元模型

本文基于ABAQUS有限元软件对算例桥梁进行有限元建模，如图2所示。由于在研究桥墩损伤状态时简易梁单元、弹簧单元即可保证所得数据的准确性[9]，本文有限元模型中主梁、桥墩及承台采用Beam31梁单元模拟，桥墩和支座以及主梁和支座之间采用K-Coupling耦合连接。桥梁支座采用ABAQUS自带的Connector中的Bushing连接单元模拟，能够较好的模拟支座力学性能，图3为Bushing连接单元示意图。Beam31梁单元采用Shi等[10]开发的适用于空间梁单元隐式算法的材料子程序iConcrete04和iSteel01，分别模拟混凝土和钢筋的本构关系，其能较好的模拟混凝土和钢筋材料的力学性能。本研究将桥墩承台以下固定，忽略桩土作用的影响。桥墩动水压力采用附加质量法[11]模拟

(1)

式中:Mw为附加动水质量;CM为惯性系数;ρ为海水密度;D为桥墩直径。

图2 桥梁有限元模型Fig.2 Finite element model of the bridge

图3 Bushing连接单元图Fig.3 Bushing connection element

2 海底空间变化地震动及其转动分量的模拟

研究将海水层视为理想流体，基于基本流体方程与一维波动理论[12-13]，实现了包含海水层的无限半空间海底场地的模拟[14]. 分别选取NGA-West2数据库中陆地场地和海底地震观测系统(SEMS)所在海域场地数据，并对场地参数进行相似化处理，建立陆地与海底的场地模型。

由于桥梁各墩柱之间距离远小于桥梁与震源之间的距离，因此假定桥梁所处的不同基岩位置功率谱密度保持一致。针对所处场地，如果仅考虑其线弹性反应，j点地震动的自功率谱密度函数Sjj(ω)可表示为[15]

Sjj(ω)=Sbr(ω)|Hj(iω)|2

(2)

式中:Sbr(ω)为基岩地震动的功率谱密度函数；|Hj(iω)|2为j点处地震动的传递函数，可根据文献[6]得到。

所处场地两模拟点之间的地震动互功率谱密度Sjk(iω)为

(3)

式中:上标′表示共轭复数;γj′k′(iω)表示两点间的相干损失。

基于上述理论，得到包含多个模拟点功率谱密度函数的矩阵，然后将其分解为复数下三角矩阵及Hermitian矩阵，即可得到在其频域内j点的地震动[16]，表示为

(4)

其中：

(5)

(6)

式中，αjm(ωn)、Bjm(ωn)分别表示地震波所处第n个频率时的相位差和幅值。

最后利用傅里叶逆变换将Uj(iωn)转换至时域内，至此得到j点处的地震动平稳加速度时程。

为精细化模拟跨海桥梁的地震反应，本文以多点激励的方式施加地震荷载，不同桥墩位置分别输入了考虑行波效应与相干效应等的地震荷载[17-18]。

各桥墩位置输入的海底与陆地地震荷载是在相同基岩地震荷载作用下，通过上述海底与陆地场地传递函数的方法模拟得到的海床与地表位置的三向地震动荷载。限于篇幅，文中仅列出1#墩底顺桥向、横桥向和竖直方向的陆地地震动及其相应的海底地震动加速度时程，如图4所示。可以看出，相同基岩地震激励下海床与地表位置的三向地震加速度时程曲线相差较大，海底地震动2个水平向分量的PGA大于陆地地震动。海底地震动顺桥向和横桥向PGA分别为3.61 m/s2与3 m/s2；陆地地震动分别为2.47 m/s2和1.98 m/s2。同时海底地震动竖向分量的PGA(0.6 m/s2)明显小于陆地地震动(0.92 m/s2)，即海底地震动的峰值加速度明显小于陆地地震动，该特性与海底实测记录及理论分析结果吻合。为保证输入的海底与陆地地震荷载具有可比性，本文将海底与陆地纵桥向(三向分量PGA最高向)加速度时程曲线的PGA调幅至相等数值，并对横桥向与竖向分量做等比例调幅。

3 易损性分析

本文为研究海底与陆地地震动作用下的桥墩易损性，将前文得到的各墩底陆地、海底地震动进行输入。最终确定2个工况，工况1为陆地地震动输入，工况2为海底地震动输入。

3.1 定义构件损伤状态

合理确定构件损伤状态对准确评价桥梁结构的抗震性能十分重要，本文选取具有代表性的边墩1#、7#，次边墩2#和中墩4#的墩顶漂移率(墩顶最大变形与墩高的比值)作为衡量算例桥梁抗震性能的指标，将构件损伤状态划分为轻度损伤、中度损伤、严重破坏、倒塌四个等级，表2为桥墩各损伤阶段的墩顶漂移率范围[19]。

表2 桥墩破坏极限Tab.2 Definition of damage states for bridge piers

需要说明的是，支座作为桥梁工程的地震易损构件一般便于检修和更换。而对近海桥梁而言，桥墩震后的损伤状态评估、修复则极为困难，桥墩地震损伤状态的评定对确保近海桥梁工程的地震安全具有极其重要的意义，因此本文以桥墩作为易损构件进行分析。

3.2 地震需求分析

文中基于概率性地震需求分析方法(PSDA)对算例近海桥梁进行易损性分析，由于易损性分析方法要求范围较大的地震动强度分布，本文取地震峰值加速度0.1g作为基准，海、陆地震动均以0.1g为加速度峰值增量进而调幅生成峰值加速度为0.1g～1.6g范围内的海陆地震动。通过式(11)进行回归分析，得到桥梁的概率需求模型

lnEDP=lna+blnIM

(7)

式中:EDP为桥墩响应；IM为地震动强度指标；a、b为统计回归系数。

4 桥墩易损性对比分析

本文以峰值加速度PGA作为衡量地震动强度的指标，墩顶漂移率作为评价桥墩损伤状态的指标，通过式(12)和(13)计算各桥墩的易损性曲线

Pf=P(DI≥LS|IM)=

(8)

(9)

4.1 海底与陆地地震动作用下桥墩易损性对比

为研究海底地震动区别于陆地地震动对桥梁构件易损性的影响，本文分工况1(陆地地震动)，工况2(海底地震动)对桥梁进行地震动输入，绘制易损性曲线进行分析。

以中墩4#与边墩7#为例，绘制海底地震动与陆地地震动作用下两桥墩损伤概率，如图5所示。其中图5(a)、5(b)为4#与7#桥墩在两工况下的易损性曲线，图5(c)、5(d)分别为4#与7#桥墩在海底地震动较陆地地震动下的损伤概率增幅。

图5(a)、(b)为海底地震动与陆地地震动作用下的桥墩易损性曲线。可见，两种地震动作用下，桥墩的易损性曲线变化规律基本一致，四种损伤状态下，4#、7#墩在海底地震动作用下的损伤概率均较陆地地震动下的损伤概率有明显提高。轻度损伤、中度损伤状态概率增幅更为明显，严重破坏、倒塌状态由于其发生概率较低、地震动强度需求较高而导致增幅较小。

图5(c)为4#墩海底地震动相较于陆地地震动造成的损伤概率增幅柱状图。可见，轻度损伤状态下：PGA达到0.2g时，增幅超过5%并逐渐增大，增幅较大的区间为0.4g～1.0g，其增幅均在10%以上，其中增幅峰值出现在PGA为0.6g时，高达23.44%。对于中度损伤状态，PGA达到0.4g后，增幅逐渐增大，并于1.1g时增幅峰值达到12.03%，而后逐渐降低。对于严重破坏状态，PGA在1.3g～1.4g时，增幅最大，约为5.05%。在等于或略高于桥梁抗震设防等级的地震动作用下，桥梁更易发生轻度损伤、中度损伤，而在这一范围内，海底地震动对桥墩易损性有显著提高。可见，针对近海桥梁易损性，基于海底地震动进行分析极为必要，以陆地地震动代替海底地震动进行分析则易低估桥梁构件损伤概率。

结合图5(d)，7#墩海底地震动相较于陆地地震动的损伤概率增幅柱状图，并根据前文所述可见：海底地震动对不同墩柱的损伤概率均有明显提升作用，但不同墩柱之间由于支座、支座与桥墩的承载能力、连接方式的不同，其在地震动作用下表现出较为明显的响应差异。7#墩损伤概率增幅峰值出现在中度损伤状态，为10.34%。而对于在4#墩中表现最为敏感的轻度损伤状态，在7#墩中增幅则有明显减低，峰值仅为4.31%。同时，轻度损伤状态下，海底地震动较陆地地震动引起的桥墩损伤概率增幅峰值对应的PGA也有明显提高，为0.9g～1.0g(4#墩为0.6g)。对于严重破坏状态，PGA超过0.5g后，随PGA增加，损伤概率增幅逐渐增大，至PGA为1.4g时，增幅达到7.0%，大于4#墩的损伤概率增幅峰值(5.05%)。综上可见，海底地震动对7#墩中度损伤概率的影响较大，而对其轻度损伤概率的影响较4#墩明显变小。

4.2 海底地震动激励对不同桥墩之间响应差异的影响

桥梁不同墩柱由于其与支座连接方式、所处局部场地等多种因素影响而表现出明显的响应差异，该响应差异是否受到地震动种类影响尚不可知。因此，本节重点研究易损墩柱在海底与陆地地震动作用下是否会产生变化。分别以边墩1#、次边墩2#和中墩4#为例，分析三者在海底、陆地地震动作用下，轻度损伤、中度损伤状态下的易损性曲线并绘于图6(a)、(b)。

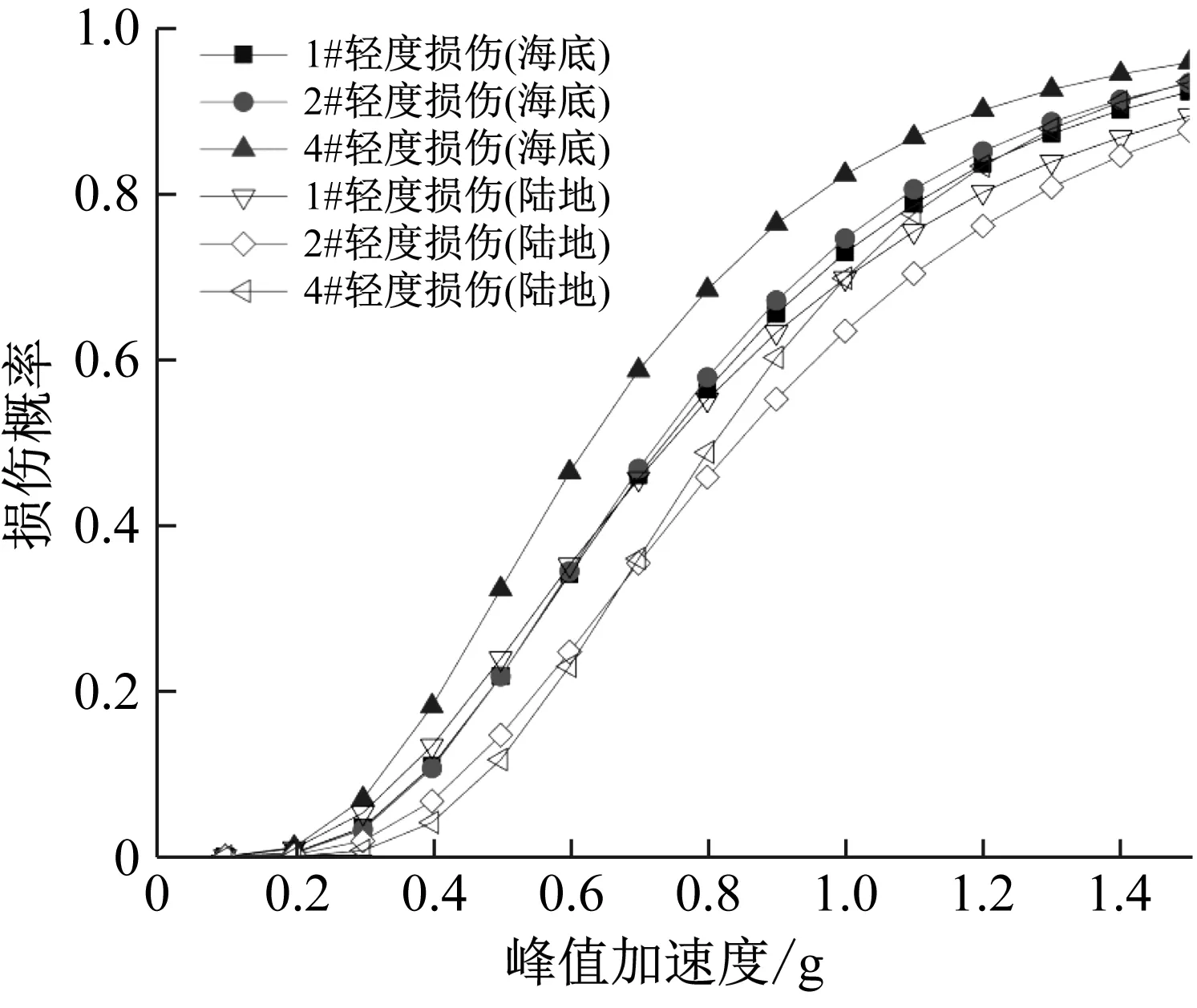
(a) 轻度损伤易损性曲线

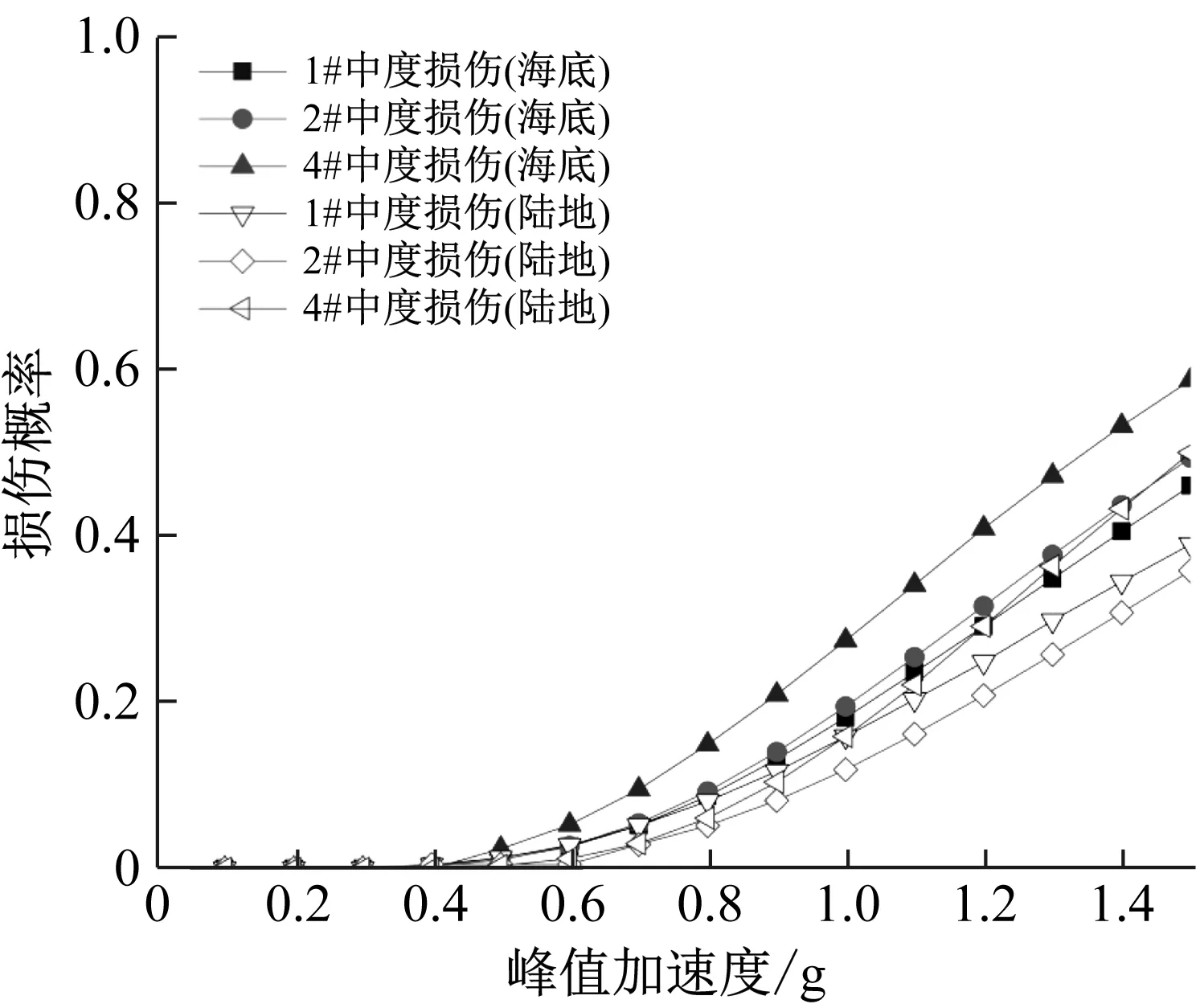
(b) 中度损伤易损性曲线图6 不同墩柱响应差异的易损性对比曲线Fig.6 Vulnerability comparison curve of different pier and column responses

由图6(a)可知，不同墩柱的响应在海底地震动、陆地地震动作用下的表现有显著区别。轻度损伤状态，海底地震动作用下中墩4#的损伤概率最高，1#墩与2#墩的损伤概率差别不大且明显小于4#墩的损伤概率，即4#墩为最易损构件。而陆地地震动作用下，PGA小于1.0g时，1#墩为最易损构件，PGA大于1.0g时，4#墩则成为最易损构件。观察图仍6(b)可见：在中度损伤状态下，海底地震动输入下，4#墩仍然为最易损构件；而陆地地震动作用下，PGA大于1.0g时，4号墩为最易损构件，PGA小于1.0g时，1号墩则为最易损构件。这表明，海底地震动输入下桥梁的易损构件极有可能与陆地地震动输入下不同，以陆地地震动输入研究近海桥梁抗震性能会错估桥梁易损位置。

总体来说，对近海桥梁工程而言，海底地震动输入较陆地地震动输入会加剧桥墩损伤。其次，海底地震动输入下易损桥墩的位置也与陆地地震动输入下不同。

幅柱状图，并根据前文所述可见：海底

5 结 论

本文通过对陆地、海底地震动进行模拟，以桥墩为研究对象，采用基于PSDA的易损性方法对比分析海底地震动与陆地地震动对近海桥梁结构易损性的影响，主要结论如下：

(1) 海底地震动会显著增加近海桥梁的桥墩损伤概率。轻度损伤状态下，海底地震动引起的桥墩损伤概率较陆地地震动下的损伤概率增幅最大可达23.44%。而针对中度损伤及更严重的损伤状态，因对地震动强度需求较高，海底地震动引起的损伤概率较陆地地震动下损伤概率的增幅变小，但最高仍可达12%，不应忽视。

(2) 海底地震动作用下，近海桥梁损伤概率最高的墩柱可能与陆地地震动下损伤概率最高的墩柱不同，以陆地地震动进行近海桥梁抗震性能研究可能会错估桥梁易损位置，使得研究结论不准确。