基于注意力GRU算法的滚动轴承剩余寿命预测

2021-09-19姚德臣李博阳刘恒畅姚娟娟皮雁南

振动与冲击 2021年17期

姚德臣，李博阳，刘恒畅，姚娟娟，皮雁南

(1.北京建筑大学机电与车辆工程学院，北京 100044；2.北京建筑大学城市轨道交通车辆服役性能保障北京市重点实验室，北京 100044；3.北京市地铁运营有限公司，北京 100044)

随着科学技术的不断发展以及工程应用的迫切需要，越来越多的大型机械装置被设计并制造出来服务于人类社会之中，旋转机械装置作为其中的一类，在冶金，航空航天，轨道交通，电力，石油化工等众多领域中有着广泛的应用。滚动轴承作为旋转机械中最为常见的零件之一，其状态的好坏对于维持整个旋转机械运行的平稳性与安全性有着重要的意义，但相关研究表明，滚动轴承同样也是最容易产生故障的零件。据统计，在使用滚动轴承的旋转设备中，大约有45%～55%的机械故障都是由滚动轴承引起的[1]。

因此，针对滚动轴承的剩余寿命预测，已经成为了机械故障诊断领域热点话题之一，许多滚动轴承剩余寿命预测方法也随之被提出应用于此。例如，徐继亚等[2]提出的融合KPCA与信息粒化的SVM预测方法，刘波等[3]提出的基于连续型HMM和PSO-SVM的预测方法，马海龙[4]提出的基于主元特征融合和SVM的预测方法，者娜等[5]提出的KPCA和改进SVM结合的预测方法，这些方法大都以支持向量机(support vector machine，SVM)为核心算法并加以改进实现预测，然而随着先进制造技术的发展，智能化旋转机械设备的大量出现，滚动轴承的运行工况也变得更加复杂多变[6]，这些传统预测方法的缺点也突显出来，传统方法需要依靠随轴承寿命退化敏感的特征作为输入，而不能将多种特征综合起来进行自主学习，这就导致了其过于依赖人工经验进行特征提取，降低了预测的智能性[7]；且传统模型结构简单，复杂程度低，学习能力有限，在预测结果达到一定精度后因为模型自身问题而进入瓶颈期，修改超参数也不能使预测精度进一步提高，特别是面对非线性，非平稳信号时，并不具备很好的表现。

随着深度学习近年来的发展，一些深度神经网络也被提出用于滚动轴承剩余寿命预测，例如张继冬等[8]提出的全卷积层神经网络的预测方法，以此来避免人工提取特征指标，依靠加深神经网络结构层次，融入复杂机制自动提取信号特征进行预测。然而，原始信号中的大量噪声会影响预测结果，而且为了充分提取信号特征而不断增加网络结构层次，从而导致网络整体复杂性的增加，不仅使计算量增大，对设备要求更高，同时使网络更加难以优化，最为重要的是原始振动信号不具有明显的序列性，况且这些神经网络自身缺乏序列数据处理能力，并不适合实际工程应用。

因此，本文提出一种Attention机制融合GRU算法的方法来进行滚动轴承剩余寿命预测，试验结果表明，改进后的GRU模型学习能力更强，处理序列数据的表现更好，更加适用于滚动轴承剩余寿命预测。

1 理论分析

1.1 技术路线

本文提出利用循环神经网络对时序数据处理能力实现对滚动轴承的寿命预测，主要技术路线为首先从原始信号中提取多种特征指标，将这些特征指标归一化处理后构建多特征数据集，并划分为训练集和测试集，其次进行GRU算法模型的构建，并引入Attention机制增强模型表现，最后，将训练集数据输入模型，对模型进行训练，降低损失函数值(loss)，确定最优结构参数，待模型训练完成后，输入测试集数据，用于评估模型预测效果。图1为预测方法流程图。

图1 预测方法流程图Fig.1 Flow chart of prediction method

1.2 特征提取

首先，提取原始振动信号中十六种时域特征指标构建数据集。表1为所提特征信息。其原因包括：

(1) 构建特征数据集，可大幅降低原始数据量，减少计算量，降低噪声影响，提升效率，从而避免了为追求神经网络提取特征能力而不断堆叠网络层次，加深网络结构，造成网络难以优化的问题。

(2) 在实时动态的监测过程中，信号的时域特征能够最直接且明显的反映滚动轴承的退化状态。

(3) 以时域特征构建的数据集其自身的序列性和变化的趋势性最为显著，更适合GRU网络结构的输入。

(4) 单一特征反映轴承退化情况有限，而且可能引起信息的丢失[9]。

(5) GRU算法的侧重点在于学习和分析数据的序列趋势和内在联系，且能够自主决定特征信息的保留与舍弃，因此不需要专门去提取某种敏感特征，相反，多种特征能够使模型学习的内容更加充分，表现程度往往也更贴合实际。

表1 特征提取Tab.1 Feature extraction

1.3 数据归一化处理

数据的归一化(normalization)又叫做数据的离差标准化，是将数据缩小至[0,1]区间之内，归一化经常被用于一些评价指标处理之中，去除单位对数据的限制，便于不同指标之间的比较或加权。数据归一化后的优点如下：

模型一定程度上会提升收敛速度，提高预测精度。

对于某些神经网络，归一化后可有效防止梯度爆炸。

其计算公式如下

(1)

式中:max为所有样本数据的最大值;min为所有样本数据的最小值。数据归一化处理后构建特征数据集。

1.4 GRU算法介绍

针对普通RNN结构在反向传播过程中遇到的梯度消失或梯度爆炸的问题，Hochreiter等[10]提出了一种长短期记忆网络(long short-term memory，LSTM)，以其独特的“三个门”结构成功的解决了这个问题，LSTM的出现为RNN的发展做出了开创性的贡献，门控循环单元(gated recurrent unit，GRU)[11]作为LSTM的变体网络，它的出现，进一步推动了循环神经网络的发展。图2为RNN结构图。图3为LSTM结构图。

图2 RNN结构图Fig.2 RNN structure diagram

图3 LSTM结构图Fig.3 LSTM structure diagram

相较于LSTM，GRU网络比较大的改动在于：

(1) GRU网络将单元状态与输出合并为隐藏状态，依靠隐藏状态来传输信息。

(2) GRU网络将LSTM中的遗忘门和输入门整合成为了一个更新门限[12]。

正是由于这两个创新点的引入，使得GRU模型较LSTM模型具有如下优点：参数量减少了三分之一，不容易发生过拟合的现象，在一些情况下可以省略dropout环节；在训练数据很大的时候可以有效减少运算时间，加速迭代过程，提升运算效率；从计算角度看，其可扩展性有利于构筑较大的模型。

同时，GRU继承了LSTM处理梯度问题的能力，其门结构可以有效过滤掉无用信息，捕捉输入数据的长期依赖关系[13]，在处理序列问题上具有非常出色的表现。图4为GRU结构图。

图4 GRU结构图Fig.4 GRU structure diagram

图4中:σ表示sigmoid函数;sigmoid函数是GRU网络的激活函数之一，其能够将变量控制在0～1之间，在网络结构中，以0代表任何变量都不能通过，反之，以1代表任意变量都可以通过;tanh代表双曲正切函数，也是GRU网络中的激活函数，用于实现非线性变换;“⊗”表示两项相乘;“⊕”表示两项相加。sigmoid函数与tanh函数表达式如下

(2)

(3)

更新门zt的作用是决定丢弃哪些旧信息和添加哪些新信息，其计算公式为

zt=σ(Wz·[ht-1,xt])

(4)

如图5所示，此步骤先将上一时刻的输入信息ht-1与当前时刻的输入信息Xt与权重矩阵W相乘进行线性变换，然后将数据送入更新门zt之中，经过激活函数sigmoid的作用后，输出一个0～1之间的值，此环节决定了有多少过去的信息可以继续传递到未来。

图5 更新门信息流向图Fig.5 Update gate information flow diagram

重置门rt的作用是决定忘掉历史信息的程度，其计算公式为

rt=σ(Wr·[ht-1,xt])

(5)

如图6所示，与更新门zt类似，先将上一时刻输入信息ht-1与当前时刻输入信息Xt与权重矩阵W相乘进行线性变换，只是两次权重的数值和作用不同，然后将数据送入重置门中经sigmoid函数作用，此环节决定了有多少历史信息不能传递到下一时刻。

图6 重置门信息流向图Fig.6 Reset gate information flow diagram

备选状态主要是当前时刻的输入信息，相当于记忆了当前时刻的状态，其计算公式为

(6)

图7 备选信息流向图Fig.7 Alternative information flow diagram

最后，隐藏状态决定当前时刻需要输出的信息，其计算公式为

(7)

式中:W代表权重矩阵;ht-1代表上一时刻隐藏层输出;Xt代表当前时刻输入;“*”代表矩阵乘法;“·”代表点乘。

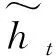
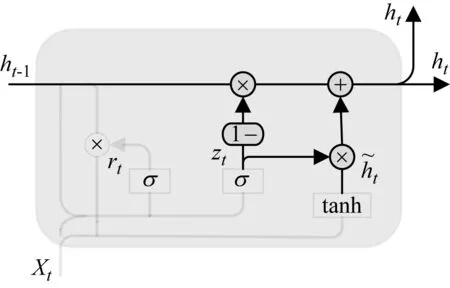
图8 最终输出信息流向图Fig.8 Final output information flow diagram

1.5 注意力机制

注意力机制是深度学习中的一种仿生机制，它的提出是由人类观察环境的习惯规律所总结而来的，人类在观察环境时，大脑往往只关注某几个特别重要的局部，获取需要的信息，构建出关于环境的描述，而注意力机制正是如此，其本质就是对关注部分给予较高权重[14]，从而获取更有效的信息，从数学意义上来说，它可以理解为是一种加权求和。注意力机制的主要作用包括：

(1) 对输入序列的不同局部，赋予不同的权重。

(2) 对于不同的输出序列局部，给输入局部不一样赋权规划。

在滚动轴承寿命预测中，考虑到不同时刻的特征对下一时刻寿命预测的贡献不同，所以在GRU模型中增加注意力层，以加强重要时刻特征对寿命预测的贡献，将此Attention-GRU模型应用于滚动轴承剩余寿命预测，以期望通过注意力机制自我调节使预测得到一个更好的结果。图9为注意力机制图。

图9 注意力机制Fig.9 Attention mechanism

加权求和公式

(8)

式中:hi为隐藏层输出;ai为注意力权重分配;c就是一个加权求和的过程。

2 试验验证

2.1 基于XJTU-SY数据集的试验验证

为证明将构建特征指标数据集融合改进GRU算法应用于滚动轴承剩余寿命预测的有效性，设计试验进行验证，数据来源于XJTU-SY的滚动轴承加速寿命试验数据集[15]，此数据集包含了3种工况下的15个滚动轴承的全寿命周期信号并明确标注了每个轴承的失效部位，试验用轴承类型为LDK UER204滚动轴承。试验中设置采样频率为25.6 kHz，采样间隔为1 min，每次采样时长为1.28 s。图10为轴承加速寿命试验平台。

图10 轴承加速寿命试验平台Fig.10 Bearing accelerated life test platform

在验证过程中，选用第三种工况下的第二组数据集，该数据集共有2 496个样本，每个样本中有两列数据，分别是轴承的横向和垂向振动信号，每列有32 769个采样值，轴承实际剩余寿命为41 h36 min，试验结束至轴承失效时，出现内圈，外圈，保持架，滚动体四种复合故障。由于在试验过程中施加的力为径向力，因此，横向振动信号更能反映轴承的退化状态[16],本文以所有样本的横向振动信号为研究对象。首先，利用MATLAB软件对全部样本进行时域特征提取，针对每一个样本数据计算其16种时域特征，共计2 496组，作为振动信号特征提取后的特征数据集并储存为csv文件格式，并将特征数据集分为训练集和测试集，其中，前2 400组样本作为训练集对模型进行训练，剩余96组作为测试集输入。

GRU模型基于TensorFlow开源深度学习框架进行设计，使用Intel(R) Core(TM) i5-9300H CPU(主频2.4 GHz)，WIN10 64位操作系统，NVIDIA GTX1660Ti显卡，主机上安装了CUDA 10.0,Cudnn7.3对显卡运算进行加速。

试验中GRU模型选取Adam优化器对训练loss进行优化，Adam是目前TensorFlow架构中比较流行的一种优化器，相较于其他优化器能够自适应参数学习，具有收敛速度快，对内存需求小，能较好处理噪音样本等优点。图11为两种常用优化器在训练过程中的loss值下降曲线。

图11 训练集loss曲线Fig.11 Loss curve of training set

为了更好评估构建特征指标数据集融合改进GRU模型的预测效果，本文以平均绝对误差(mean absolute error，MAE)和均方根误差(root mean square error，RMSE)为指标进行评估[17]，并计算了不同模型训练时长。

平均绝对误差计算公式

(9)

均方根误差计算公式

(10)

本试验主要测试融合注意力机制的GRU模型在预测滚动轴承剩余寿命这类时间序列问题上的表现，并与其它模型预测效果进行对比。图12为几种模型预测效果图。表2为在XJTU-SY数据集上的评估数据。

表2 不同模型在XJTU-SY数据集上评估数据Tab.2 Different models evaluate data on XJTU-SY data set

画出不同模型预测效果对比图，并利用MATLAB软件画出改进GRU模型在XJTU-SY数据集上预测效果的拟合曲线。如图13和图14所示。可以看出预测结果非常贴近实际寿命曲线。

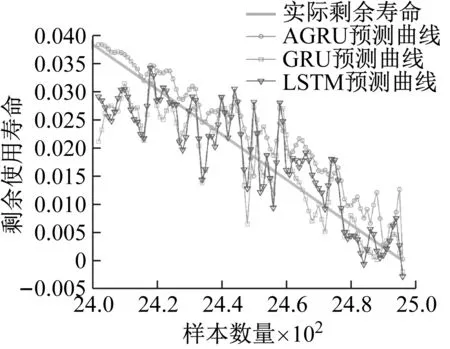
图13 不同模型对XJTU-SY数据集预测效果对比Fig.13 Comparison of prediction effects of different models on XJTU-SY data set

图14 XJTU-SY数据集拟合效果图Fig.14 XJTU-SY data set fitting rendering

2.2 基于IMS数据集的试验验证

为进一步验证该方法应用在滚动轴承剩余寿命预测上的可行性，选择辛辛那提大学智能维护中心(intelligent maintenance systems，IMS)的第二组轴承全寿命试验数据[18]增设一组试验，该组数据共984个样本，采样频率为20 kHz，采样间隔10 min，采样时间为1 s，试验轴承为Rexnord ZA-2115双排轴承，恒定转速为2 000 rad/min，附加径向载荷6 000磅，轴承四通道排列，试验结束至失效试验时，一号轴承发生外圈单一故障，实际剩余寿命为164 h。图15为试验装置示意图。

图15 试验装置示意图Fig.15 Schematic diagram of experimental device

在特征指标数据集构建与训练标签的构建上均采用上述所提方法，将984组数据的前900组作为训练集用以对模型的训练，剩余84组样本作为测试集进行预测。图16为几种模型预测效果。表3为在IMS轴承数据集上的评估数据。

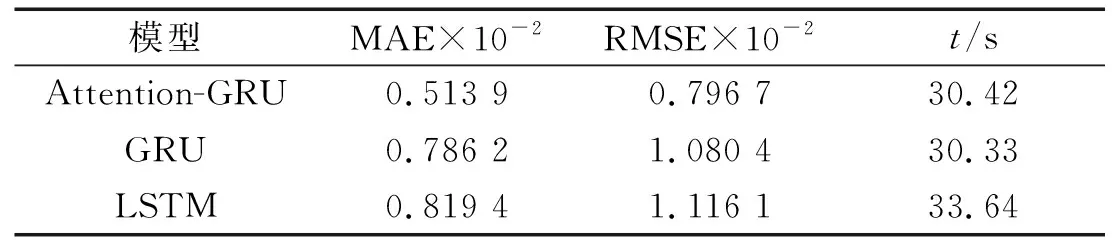
表3 不同模型在IMS数据集上评估数据Tab.3 Different models evaluate data on IMS data set

同样，画出不同模型预测效果对比图，并利用MATLAB软件拟合出改进GRU模型在IMS数据集上表现。如图17和图18所示。

图17 不同模型对IMS数据集预测效果对比Fig.17 Comparison of prediction effects of different models on IMS data set

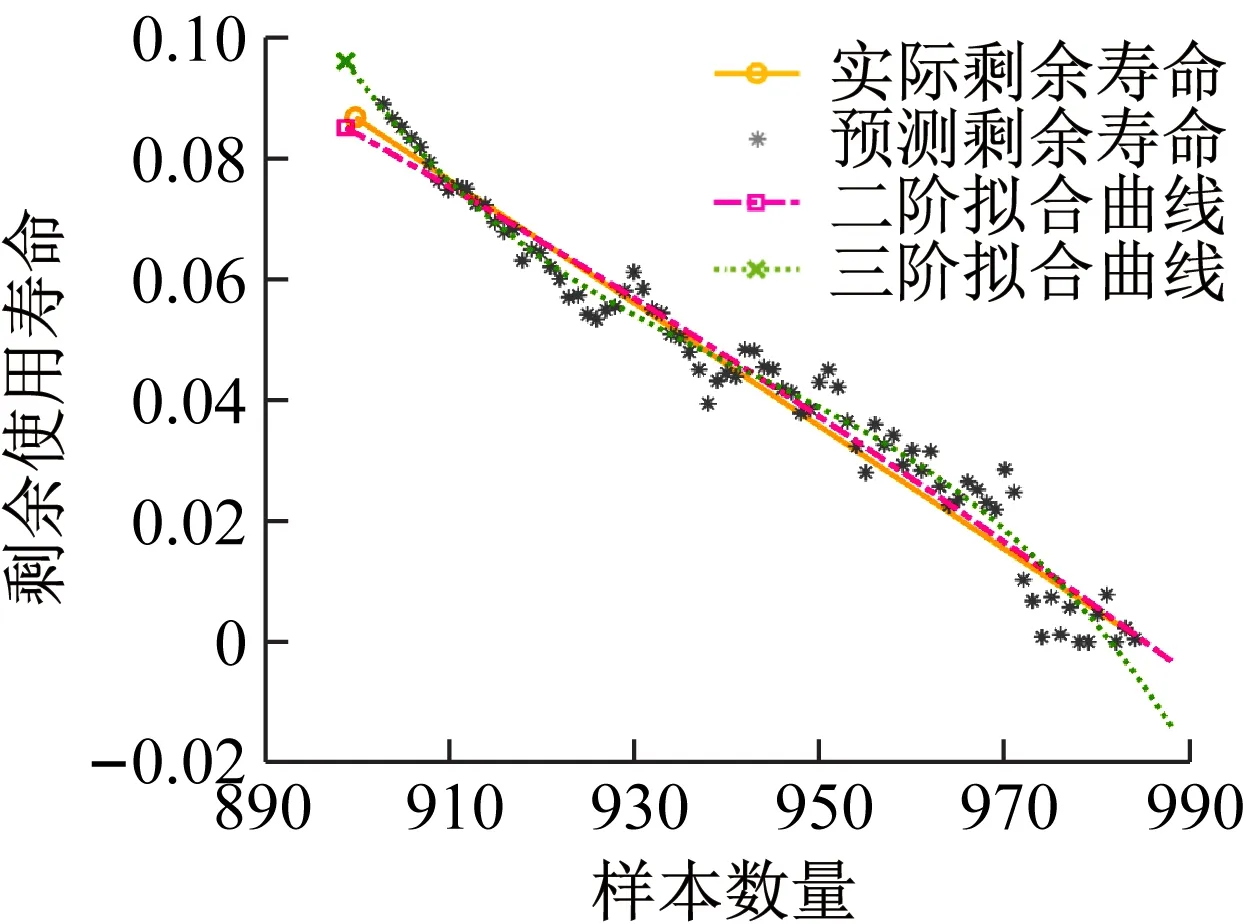
图18 IMS数据集拟合效果图Fig.18 IMS data set fitting renderings

经过计算后可得，在XJTU-SY数据集上，Attention-GRU模型相比GRU与LSTM模型，其MAE和RMSE两项指标分别提升了16%和25%左右，在IMS数据集上，这两项指标分别提升了35%和27%左右。

此外，融入Attention机制的GRU算法在预测精度显著提升的同时并未对训练时间产生很大影响，且由于自身参数量更少，GRU模型无论改进或未改进其训练时长上均快于LSTM模型，经过多次试验后发现，在XJTU-SY数据集上，这一提升平均在6 s左右，在IMS数据集上，这一提升平均在3 s左右，如果数据量级更大，这一提升将会更加显著。