基于Fluent的管道车振动运移水力特性仿真分析
2021-09-19张春晋张学琴李永业孙西欢
张春晋, 张学琴, 张 敏, 李永业, 孙西欢
(1.黄河水利科学研究院水利部黄河下游河道与河口治理重点实验室,郑州 450003;2.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098;3.太原理工大学 水利科学与工程学院,太原 030024;4.济南黄河河务局章丘黄河河务局,济南 250200;5.黄河水利委员会规划计划局,郑州 450003)
目前,传统运输方式将造成交通阻塞、能源危机与环境污染等问题,严重制约着社会经济与生态环境的可持续发展[1]。(筒装料管道水力输送是一种低碳环保的新型运输方式,其原理是将物料盛装于管道车,依靠管道流体的动能推动管道车长距离运输。
近年来,许多国内外学者对筒装料管道水力输送展开大量研究。试验方面:李永业等[2]探讨了不同型号管道车振动运移水力特性。Kruyer等[3]分析了管道车结构变量与平动速度的函数关系。王锐等[4]将管道车振动运移划分为四个阶段。Latto等[5]探究了管道车振动运移的平动速度比、压降比及能耗比对管道流场特性的影响。井元昊等[6]提出了管道车振动运移时管道流体最佳雷诺数的概念。Lenau等[7]研究了引起圆柱状管道车在障碍物作用下保持倾斜状态的临界启动流速。由于仪器限制,模型试验并不能完全获得管道流场水力特性。仿真方面:Barthès-Biesel[8]结合湍流基本关系,探讨了管道车振动运移时管道的系统能耗。Khalil等[9]求解了单个管道车振动运移的本构方程。Asim等[10]对管道车振动运移时水力特性进行了计算。目前,数值模拟研究仅考虑了管道车结构响应对管道流场的影响,并未考虑两者的耦合作用。实际上,管道车与管道流体存在着明显耦合作用,即一方面管道车在管道流体作用下产生结构响应,另一方面管道车结构响应又反过来影响管道流场特性。因此,采用流固耦合分析方法十分必要。目前,流固耦合分析方法在旋转机械方面[11]取得大量成果,但是对于筒装料管道水力输送却涉及较少。为准确掌握筒装料管道水力输送流速及压强的分布特性,基于Fluent软件对管道车在平直管道振动运移水力特性进行流固耦合仿真计算,本研究将为准确评价管道车输送效果提供理论基础与技术支撑。
1 材料与方法
1.1 管道车结构
管道车由料筒、支撑体和万向滚珠组成。管道车长度和直径采用lc和dc表示。直径比为管道车与管道两者直径的比值,采用kc表示。支撑体呈等间距布置在料筒端面,从而使得管道车与管道始终保持同心状态。万向滚珠安装在支撑体末端,以减小摩擦阻力。荷载由直径为8 mm的钢珠组成。管道车结构如图1。


1.管道;2.料筒;3.支撑体;4.万向滚珠。图1 管道车结构Fig.1 Structure of a pipeline vehicle
1.2 试验系统
试验系统由动力装置、控制装置、输送装置及接收装置组成,如图2。动力装置由水箱与离心泵组成。控制装置包括电磁流量计、调压室、调节阀和制动装置。输送装置为有机玻璃管道,长度28.62 m,直径0.1 m,壁厚0.05 m。有机玻璃管道还布置有水槽,用于防止激光在管壁发生折射。接收装置由投放装置、塑料集车箱和稳流板组成。试验时,先将水流通过离心泵抽至有机玻璃管道,待流量稳定后,将管道车从投放装置注入输送管道。当管道车运行至测试断面,对管道流场流速与压强进行采集,并传输至计算机。
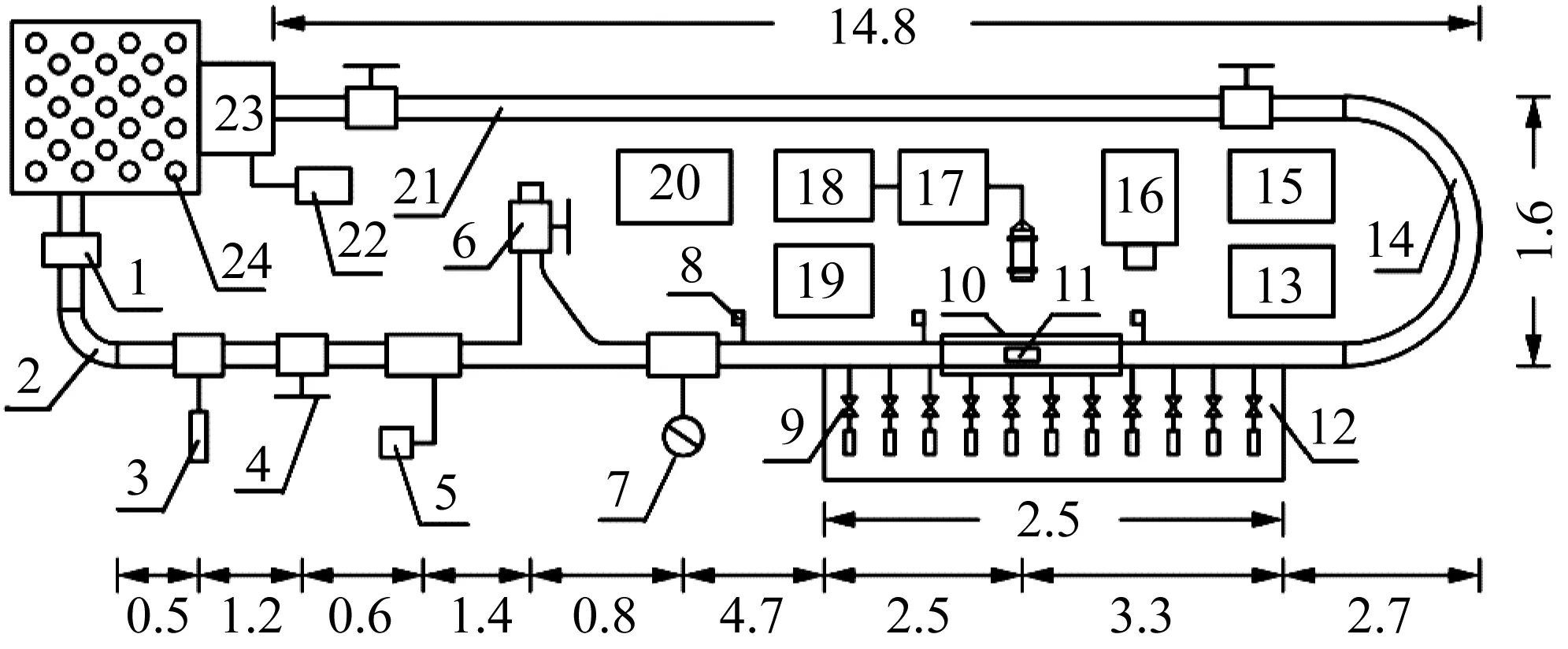
1.离心泵;2.钢管段;3.调压室;4.调节阀;5.电磁流量计;6.投放装置;7.制动装置;8.光电计时器;9.压力传感器;10.水槽;11.管道车;12.试验测试段;13.数字显示器;14.弯管;15.动态压强采集系统;16.高速摄像机;17.激光流速仪;18.信号接受平台;19.计算机;20.配电箱;21.平直管道;22.温控装置;23.塑料集车箱;24.稳流板与水箱;25.流动方向。图2 试验系统(m)Fig.2 Experimental system(m)
1.3 试验方案
管道车长度0.1 m,直径比0.4~0.9,间隔0.05。设计流量40、50、60和70 m3/h,荷载0.6 kg。试验测试段长度5.8 m,距离弯管进口断面2.7 m,距上游制动装置4.7 m。试验测试段布置4个流速测试断面,距其进口断面2.4、2.5、2.6及2.7 m,并且命名为1#、2#、3#及4#。采用激光流速仪与光电计时器测量流速分布。采用压力传感器与标准动态压强采集系统测量测压管水头。采用高速摄像机测量管道车瞬时平动速度。
2 数值计算
2.1 流体域控制方程
考虑到管道流场的复杂性,需做如下假设:①忽略流体密度变化;②忽略流体与壁面摩擦热量。流体域控制方程包括连续性方程和雷诺时均动量方程。由于RNGk-ε湍流模型能更好地处理流线弯曲程度较大的流动。因此,本文选择RNGk-ε湍流模型进行计算。在计算域近壁面区域,由于雷诺数较低,RNGk-ε湍流模型不再适用。为此,采用标准壁面函数法[12]进行处理。
2.2 结构域控制方程
管道车结构响应涉及运动状态改变与结构形态改变。运动状态改变指在流体作用下管道车产生沿管道平动运动和以管中心为轴旋转运动。结构形态改变指在流体作用下管道车应力与应变情况。管道车在平直管道运移时,其形状、大小及内部各点相对位置变化微小,可忽略不计,即将管道车视为“刚体”可达到模型求解精度。另外,若将管道车视为“弹性体”,还需设置弹性模量、泊松比及密度等物理量,这将增加模型求解运算量。通过对比运算量及求解精度,将管道车视为“刚体”较为合理,能充分体现管道车与流体的耦合作用。利用哈密尔顿原理建立结构运动学方程,设置与流体相应时间步长。流体中离散后结构动力学方程[13]可表达为
Mx″+Cx′+Kx=Fs+Fu
式中:M为质量矩阵;C为阻尼矩阵;K为刚体矩阵;Fs为非流体荷载;Fu为耦合作用力;x、x′和x″分别为节点位移矢量、速度矢量及加速度矢量。
在流体与管道车耦合界面,流体与管道车瞬时位移与瞬时应力守恒。在Fluent软件中,6DoF耦合模型原理是利用结构动力学方程求解管道车平动加速度与旋转角加速度。结构动力学方程中荷载包括流体与非流体两种荷载。流体荷载通过6DoF耦合模型计算,非流体荷载通过UDFs定义。管道流体与输送管道也存在耦合作用。管道在流体作用下,一方面不产生运动状态改变,另一方面产生的结构形态改变可忽略不计。因此,本文不考虑流体与输送管道之间的耦合作用是合理的。
2.3 求解算法
运用6DoF耦合模型和UDFs自定义函数对管道车结构响应分析,实现管道流体域数据与管道车结构域数据的实时交换。采用动网格技术对计算域网格实时修正[14]。算法步骤:①运用RNGk-ε湍流模型求解流体域;②采用UDFs对管道车振动运移过程中质量、阻力及转动惯量进行定义;③6DoF耦合模型求解管道车结构动力学方程,获得管道车瞬时平动位移、平动速度、旋转角度及旋转角速度;④利用动网格实现管道车瞬态位移;⑤将管道车瞬时平动位移、平动速度、旋转角度及旋转角速度作为下一时刻边界条件,继续求解管道车结构响应,直至管道车运移至指定位置为止。
2.4 几何模型和网格划分
采用AutoCAD软件建立筒装料管道水力输送几何模型。几何模型包括平直管道与管道车。平直管道长度5.8 m,与试验测试段长度相同。平直管道划分为进口管道、运动管道及出口管道。几何模型如图3。

注:AB为进口断面;CD为出口断面;Dc为管径;f(u)为进口断面轴向流速分布函数。图3 几何模型Fig.3 Geometric model
管道车长度0.1 m,直径0.04~0.09 m,间隔0.005 m。支撑体由细圆柱体和薄钢板片组成。半球状万向滚珠安装在支撑体外侧。在初始时刻,管道车与几何模型进口断面距离0.7 m。几何模型进口断面中心为
坐标原点,Z轴为流体方向,X轴为水平向左和Y轴为竖直向上。
计算域包括管道流体域与管道车结构域。管道流体域包括进口管道、运动管道和出口管道。进口管道与出口管道采用结构化六面体网格加密。运动管道采用与六面体网格相同尺寸的非结构化四面体网格加密。本文对流体域进行网格无关性检验[15]。
据检验结果可得由0.001 8 m和0.002 m两种网格计算的四种管道车直径比条件下几何模型进口断面平均压强相对误差都不超过0.5%。定义相邻两种体网格尺寸划分几何模型流体域,当进口断面平均压强相对误差小于0.5%时,则网格尺寸对于几何模型进口断面平均压强的影响程度可以忽略不计。因此,管道流体域网格尺寸设置为0.002 m时,已满足网格无关性检验要求[16]。
管道车结构域采用三角形网格加密。管道车动边界和管道静边界近壁面区域流速梯度大,采用矩形网格进行边界层加密。经计算,边界层第1层网格厚度0.253 mm(y+=30),比例因子1.2,网格节点9。
2.5 边界条件与数值算法
由于管径较小,因此,数值计算中忽略重力对管道内部流场的影响。环境压强为标准大气压,流体动力黏度1.062×10-3Pa·s(18 °C)。支撑体密度7.93×103kg/m,料筒密度1.2×103kg/m,万向滚珠密度7.78×103kg/m。
根据图3,对几何模型设置相应的边界条件。进口边界设置为流速入口。根据进口断面实测流速,结合UDFs自定义函数辅助定义进口断面流速分布。通过半经验公式[17]计算得到进口边界的湍流强度、湍动能及湍流耗散率等物理量。出口边界设置为压力出口。采用压强实测值定义出口断面压强分布。管壁采用无滑移边界条件[18]。管道车边界设置为动边界。采用6DoF耦合模型和UDFs自定义函数定义。UDFs除了定义管道车转动惯量和滚动摩擦阻力,还定义运移范围和初始状态。
采用PISO流速与压强耦合算法。雷诺时均动量方程、湍动能方程和湍流耗散率方程的对流项选择二阶迎风格式离散,扩散项则采用中心差分格式离散。连续性方程的压强项选择PRESTO格式离散。
3 计算结果与分析
3.1 管道车瞬时平动速度模拟与验证
图4为设计流量为50 m3/h时管道车振动运移时管道车瞬时平动速度模拟值与试验值对照图。
据图4可得:①模拟值与试验值一致,且最大相对误差不超过4.93%;②流体脉动压强的无规则波动将引起管道流体对管道车的瞬时荷载产生无规则波动变化,导致管道车瞬时平动速度呈波动变化,因此可以将管道车的运动视为振动运移;③管道车直径比增大使得其体积增大,引起管道车滚动摩擦阻力减小,进而导致其平均平动速度也增大。
3.2 管道流速模拟与验证
图5为设计流量为50 m3/h时管道车振动运移至距几何模型进口断面2.5 m时,管道轴向流速模拟值与试验值对照图。
据图5可得:①模拟值和试验值一致,且最大相对误差不超过5.36%;②管道车上游断面流速呈指数分布;③环状缝隙流在管道车车前端面出现了边界层分离,随后管道车下游流体回填边界层分离引起的空腔。因此,管道车下游流场断面流速呈中间流速低,两边流速高的变化趋势;④流速测量断面越远离管道车车前端面,则管道流场受到的边界层分离影响程度则越小,使得管道中央的回流范围减小,导致轴向流速增大;⑤管道车车中断面环状缝隙水平极轴处轴向流速分布呈先增大后减小的变化趋势。
图6为设计流量为50 m3/h时管道车振动运移时管道轴向流速分布图。图中管道流场轴向流速为模拟值。

注:Sc为管道车与几何模型进口断面的距离;vc为瞬时平动速度;θc为瞬时旋转角度;ωc为瞬时旋转角速度。图6 管道车振动运移时管道轴向流速分布图Fig.6 Axial velocity distributions of vibrational migration of a piped carriage in a pipeline
据图6可得:①管道车壁面处边界层存在逆压梯度,在逆压梯度作用下环状缝隙流在管道车车前端面近壁面产生了边界层分离现象,使得主流离开管道车的车前端面,同时管道车下游流体随机回填边界层分离产生的空腔区域。因此管道车下游流场存在明显的低流速区;②管道车振动运移时环状缝隙进口和管道车下游流场管道近壁面存在高流速区。环状缝隙进口高流速区是由管道车动边界引起流线弯曲导致。管道车下游流场管道近壁面高流速区是由回流流体在车前端面作用下向管道近壁面高速扩散形成;③管道车在平直管道内振动运移时瞬时平动速度和瞬时旋转角速度的变化幅度都较小,使得管道车与管道流体组成的耦合系统瞬态运动要素处于恒定状态。因此,不同时刻管道车振动运移时轴向流速分布基本一致;④管道车瞬时旋转角速度在±0.1 rad/s范围。由于管道车呈对称结构,使得管道车在管道内振动运移时不容易产生旋转力矩。
3.3 管道压强模拟与验证
图7为设计流量为50 m3/h时管道车振动运移时管道沿程测压管水头模拟值与试验值对照图。
据图7可得:①模拟值和试验值一致,且最大相对误差不超过1.84%;②管道流体受到管道车车后端面支撑体影响,引起管道断面突然收缩,使得管道压强降低。随后流体进入环状缝隙,在环状缝隙进口产生边界层分离,压强降低。而环状缝隙流体得到充分发展,压强升高。在管道车车前近壁面,环状缝隙流在管道车壁面产生边界层分离,导致车前近壁面压强急剧降低。最后在管道车下游,环状缝隙流与管道车下游流体相互作用,环状缝隙流体在向下游流场扩散时将动能转化为下游流体压能,使得管道车下游压强骤然回升。因此,管道车近壁面流场测压管水头形成了“W”型;③管道车上下游流场测压管水头呈降低的线性变化趋势。
图8为设计流量为50 m3/h时管道车振动运移时管道压强分布云图。图中管道流场压强为模拟值。

图8 管道车振动运移时管道压强分布图Fig.8 Pressure distributions of vibrational migration of a piped carriage in a pipeline
据图8可得:①管道车上游流体与管道车发生相互作用,使得流体将动能转化为压能,因此该区域压强将增大;②环状缝隙流与管道车下游流体发生相互掺混时,管道流场同时存在能量耗散与能量转化。能量耗散和能量转化共同引起管道车下游流场出现低压区,而能量转化使得低压区下游流体压强再次升高;③流体在环状缝隙进口断面突然束窄,主流离开料筒壁面,此时下游流体随即填补主流空腔区域,产生涡旋能耗。因此,环状缝隙进口出现了明显低压区;④环状缝隙流向上游回流时受到管道车作用,导致回流流体动能转化为其压能;⑤随着管道车振动运移时间的增长,管道车近壁面流场的压强分布呈降低的变化趋势。
3.4 能耗损失
管道车振动运移时能耗损失采用管道压降系数表示,管道压降系数指管道车存在于流体内的总能耗与空管道流体总能耗之间的比值。由于流体脉动压强的作用,管道车振动运移时压降系数随时间呈不规则波动变化。为此,采用管道平均压降系数分析管道车振动运移引起的能耗损失。图9为管道平均压降系数与直径比的变化曲线。图中管道平均压降系数为模拟值。

图9 管道平均压降系数与直径比的变化曲线Fig.9 Variation curve between average pressure drop coefficient and diameter ratio for a pipeline
据图9可得:①随着管道车直径比增加,管道平均压降系数先减小后增大,且直径比为0.75管道车振动运移引起的管道平均压降系数最小;②管道流量越大使得空管道流体沿程能耗增加,引起管道车振动运移时管道平均压降系数随流量增大呈降低的趋势。
3.5 机械效率
机械效率表示总功转化为机械能的效率。筒装料管道水力输送中总功为流体绕流管道车的局部总能耗,机械能为管道车的动能。管道车机械效率定义为管道车动能与管道流体绕流管道车的局部总能耗之间的比值。图10为管道车机械效率与直径比的变化曲线。图中管道车机械效率为模拟值。
据图10可得:①随着管道车直径比增加,管道车机械效率呈先增大后减小,且直径比0.75的管道车机械效率最高;②当管道车直径比小于0.75时,机械效率随管道流量的增加逐渐增大。当管道车直径比大于0.75时,机械效率却随管道流量的增加逐渐降低。
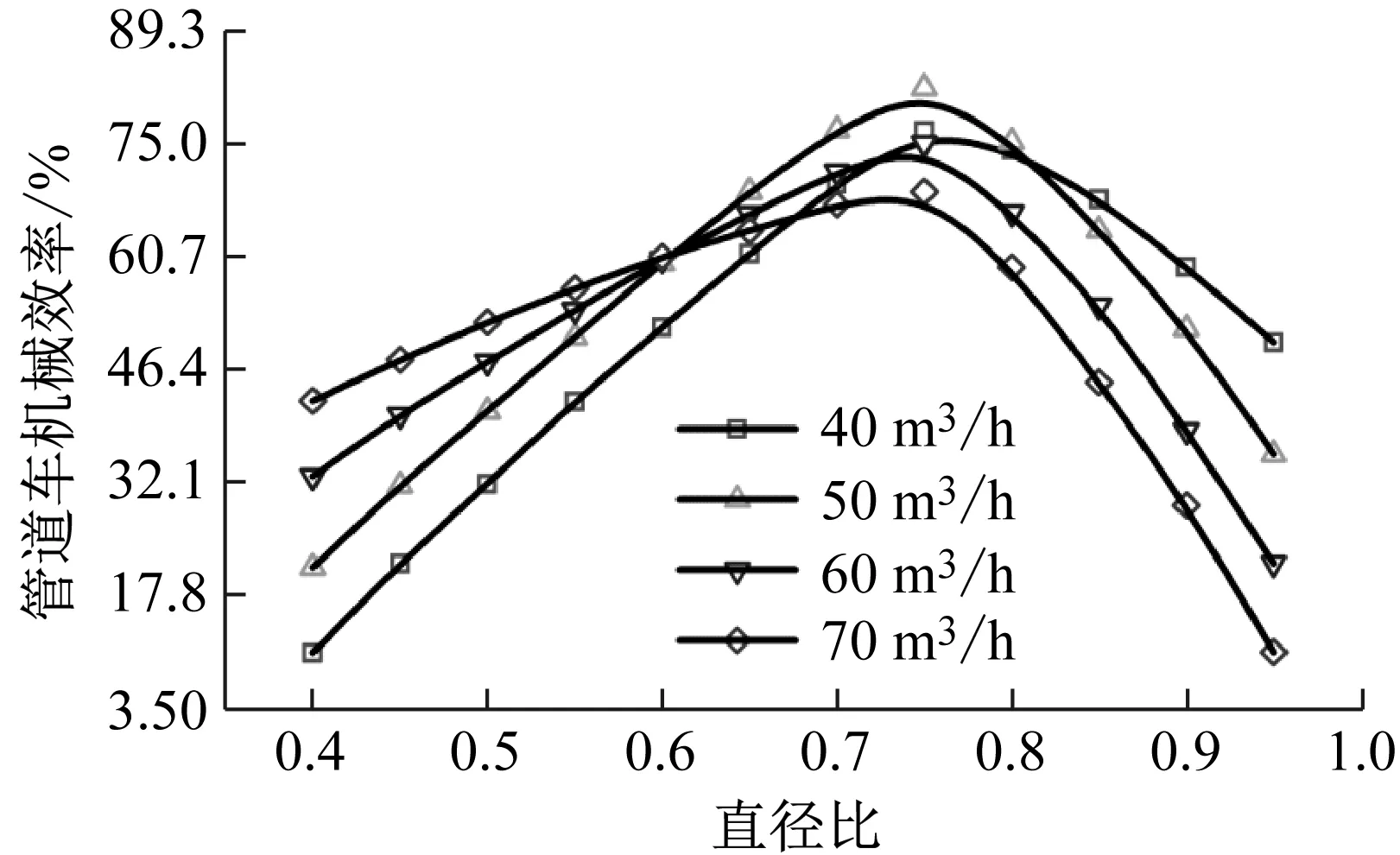
图10 管道车机械效率与直径比的变化曲线Fig.10 Variation curve between mechanical efficiency and diameter ratio for a pipeline vehicle
4 结 论
主要结论如下:
(1) 模拟值与试验值一致,且最大相对误差不超过5.36%,表明利用流固耦合数值模拟分析管道车在平直管道振动运移水力特性是可行的。
(2) 管道车在平直管道内平动速度在微小范围呈不规则波动,可将管道车运动视为振动运移。
(3) 管道车沿管道向下游振动运移时,管道车近壁面流场轴向流速分布一致,而压强分布却呈降低的趋势。随着管道车直径比增加,管道平均压降系数呈先减小后增大,而管道车机械效率呈先增大后减小。直径比为0.75的管道车在平直管道内振动运移时引起的管道平均压降系数最小,而其机械效率却处于最大。
