球形破片侵彻明胶的瞬时空腔简化模型

田浩成， 卢芳云, 李志斌， 王 硕

(国防科技大学 文理学院，长沙 410005)

破片是造成人员伤亡的主要杀伤元，而球形破片作为一种常见的预制破片被广泛应用于各种战斗部中，因此研究高速球形破片对人体的杀伤效应无论是对武器战斗部设计，还是对人体易损性分析都具有重要意义。创伤弹道学是研究诸如破片等高速投射物对生物机体创伤机理的学科，一般采用明胶等非生物靶标作为人体组织替代物来开展创伤弹道研究[1-2]。由于弹道明胶与人体肌肉组织具有相近的力学动态响应特性，本身透明，且价格相对低廉，实验室常将其制成靶标来研究“子弹”的人体杀伤能力。破片进入弹道明胶后会沿着侵彻路径形成空腔，该空腔的最大直径可膨胀到破片直径的十几倍，而整个侵彻过程及空腔往复膨胀通常在毫秒量级，因此称其为瞬时空腔[3-5]。医学上对人体进行伤情评估发现，瞬时空腔是造成生物组织创伤的主要因素之一，因此瞬时空腔模型是后续开展人体易损性分析、人员毁伤效应评估等研究工作的关键。

随着计算机技术的发展，各类计算软件也得到了极大的完善，通过有限元方法以及SPH方法等无网格方法对实际问题进行仿真，为研究难以获得试验数据、试验成本过高的复杂问题提供了新的解决途径。在创伤弹道学研究领域，国内外研究工作者已经将此类技术手段广泛应用到球形破片侵彻非生物靶标的仿真中。Dyckmans等[6]采用Autodyn对钢球侵彻肥皂的过程进行了模拟，Frissane等[7]采用SPH方法建立了钢球侵入弹道明胶的轴对称模型，并且展示出在穿透深度和速度方面的显著效果。吴建萍等[8]基于LS-DYNA软件分析了初速700 m/s的Φ4 mm实心钢球在侵彻明胶过程中的速度、能量和位移的变化规律。温垚珂等[9]也基于LS-DYNA软件分别采用Lagrange模型、SPH模型和ALE模型对钢球侵彻明胶的同一工况进行仿真，通过与试验结果的对比，得到对于此类高速投射物侵彻明胶的问题Lagrange算法最为合适的结论。罗少敏等[10]通过对不同材料的Φ4.8 mm的球形破片侵彻明胶的数值计算，分析得到了高速度、小质量的球形破片速度衰减快、能量传递大等规律，为未来战斗部杀伤元的设计提供了参考依据。

本文基于LS-DYNA的仿真结果，分析了不同初始条件下钢球在侵彻过程中的速度衰减、最大瞬时空腔演化规律，利用遗传算法将仿真数据拟合得到简化的速度衰减公式和瞬时空腔尺寸公式，通过与仿真模拟得到的瞬时空腔的比较验证了简化模型的有效性。

1 仿真模型

考虑到计算精度、计算时间等因素的影响，并根据温垚珂等对不同计算模型结果的比较，本文选取Lagrange算法进行计算。为进一步减少计算时间，提高分析效率，同时考虑到原问题的轴对称性，本文采用二维轴对称模型对原问题进行简化，建立的具体模型如图1所示。

图1中半圆形为球形破片的二维轴对称模型，破片材料参数如表1。

表1 钢球材料参数Tab.1 Material parameters of steel ball

球形破片在侵彻明胶过程中几乎不发生变形，因此将其设为刚体(*MAT_RIGID)，以节省计算时间。破片直径分别为4.8、6、7和8 mm，通过改变球形破片模型直径的方式得到不同质量和不同等效面积的计算模型。弹丸的着靶速度分别为500、724、947和1 260 m/s，并以垂直于明胶靶面的方向入射，不考虑旋转对弹丸的影响。结合以上设定，共得到16种计算工况分别对破片尺寸和着靶速度这两个影响球形破片侵彻效应的主要参量进行分析。

图1中矩形为明胶的二维轴对称模型，其半径15 cm，高30 cm。明胶的网格单元尺寸除中心区域外按照由着靶中心到外边界成比例增长的方式划分，划分方式由粗糙到精细可得到三种网格，单元数目分别共计18 361、40 581、96 761，具体划分如图2。

考虑到人体厚度基本上不超过30 cm，因此在仿真中也只关心破片在侵彻30 cm以内的速度、穿透深度和最大瞬时空腔直径等参量的规律。而在破片高速侵彻过程中，产生的高压使明胶固体出现了流体的特性，因此可以采用LS-DYNA中自带的多项式状态方程(*EOS_LINEAR_POLYNOMIAL)和弹塑性材料模型(*MAT_ELASTIC_PLASTIC_HYDRO)来描述高压状态下明胶的动态响应，其材料及状态方程所需参数如表2所示，其中C0、C1、C2和C3为线性多项式状态方程中的材料常数。

表2 明胶材料参数Tab.2 Material parameters of gelatin

2 仿真结果及分析

采用粗、中、细三种网格对着靶速度为947 m/s的Φ4.8 mm钢球侵彻明胶过程进行数值模拟，并与Wen等试验得到的速度衰减曲线和侵彻深度曲线进行对比，结果如图3所示。显然，随着网格数量的增加，数值模拟与试验结果之间的差异也随之减小，这说明数值计算对于网格具有收敛性，也验证了仿真的可靠性。由于粗网格的结果与试验结果之间存在着较大的差异，而细网格与中网格的计算结果实际上相差不算太大，中网格在侵彻深度和侵彻速度上与试验结果分别相差不到5%和10%，却大大减少了运算时间，提高了运算效率。因此本文选择采用中等网格进行仿真计算。

图4给出了Φ4.8 mm钢球着靶速度为720 m/s时的最大瞬时空腔试验结果与仿真结果的比较。通过对比，发现空腔的形状和尺寸基本吻合，进一步验证了仿真结果的准确性。

对不同工况的计算结果如图5和图6所示。由图5和图6不难看出，直径大、入射速度高的钢球穿透能力强，直径小、着靶速度高的钢球速度衰减快，并且侵彻速度的快速衰减主要在侵彻初期，钢球的直径和入射速度对之后的速度衰减影响不大。

图7给出了较小尺寸(Φ6 mm)和较高初速(1 260 m/s)钢球的速度衰减与其侵彻深度之间的关系曲线。图7(a)表明同一直径钢球在穿透等厚度明胶靶标后的速度衰减程度大致相同，但最终衰减程度也会随着入射速度的增加而小幅降低。而图7(b)展示出同一速度下钢球的直径越小，其速度衰减越严重的现象。综合上述两种规律说明高速度、小尺寸钢球穿透等厚明胶靶标的速度衰减会更加严重。

由表3可以发现，最大瞬时空腔直径与钢球直径和侵彻速度成正比例。结合图5和图6得到的规律，瞬时空腔的尺寸与球形破片损失的动能也成正比例，而着靶速度高的破片速度丧失也会更大，在明胶中穿透的时间也更短，从而传递给明胶的动量也越大。

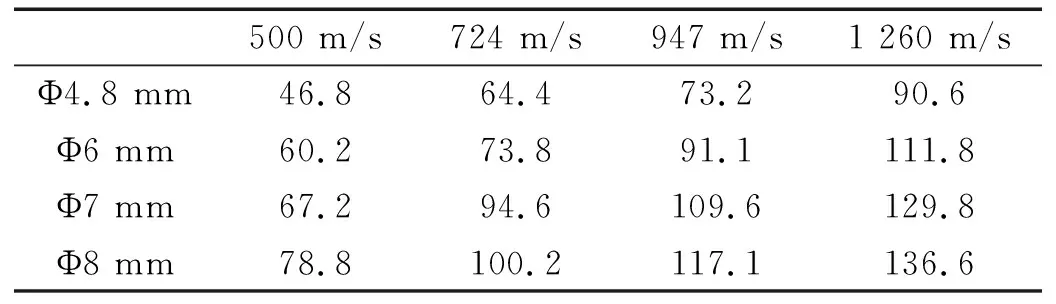
表3 不同工况下的最大瞬时空腔直径Tab.3 The maximum temporary cavity diameter under different working conditions mm

侵彻过程中的瞬时空腔半径随速度衰减的变化规律如图8所示。不难看出，与侵彻混凝土靶标过程类似，钢球侵彻明胶过程也可分为“开坑段”和“稳定段”。在“开坑段”，瞬时空腔半径差异不大，变化规律更接近二次曲线；随着速度继续衰减进入到“稳定段”，瞬时空腔尺寸与速度衰减程度基本呈线性关系且斜率随入射速度增长而变大。

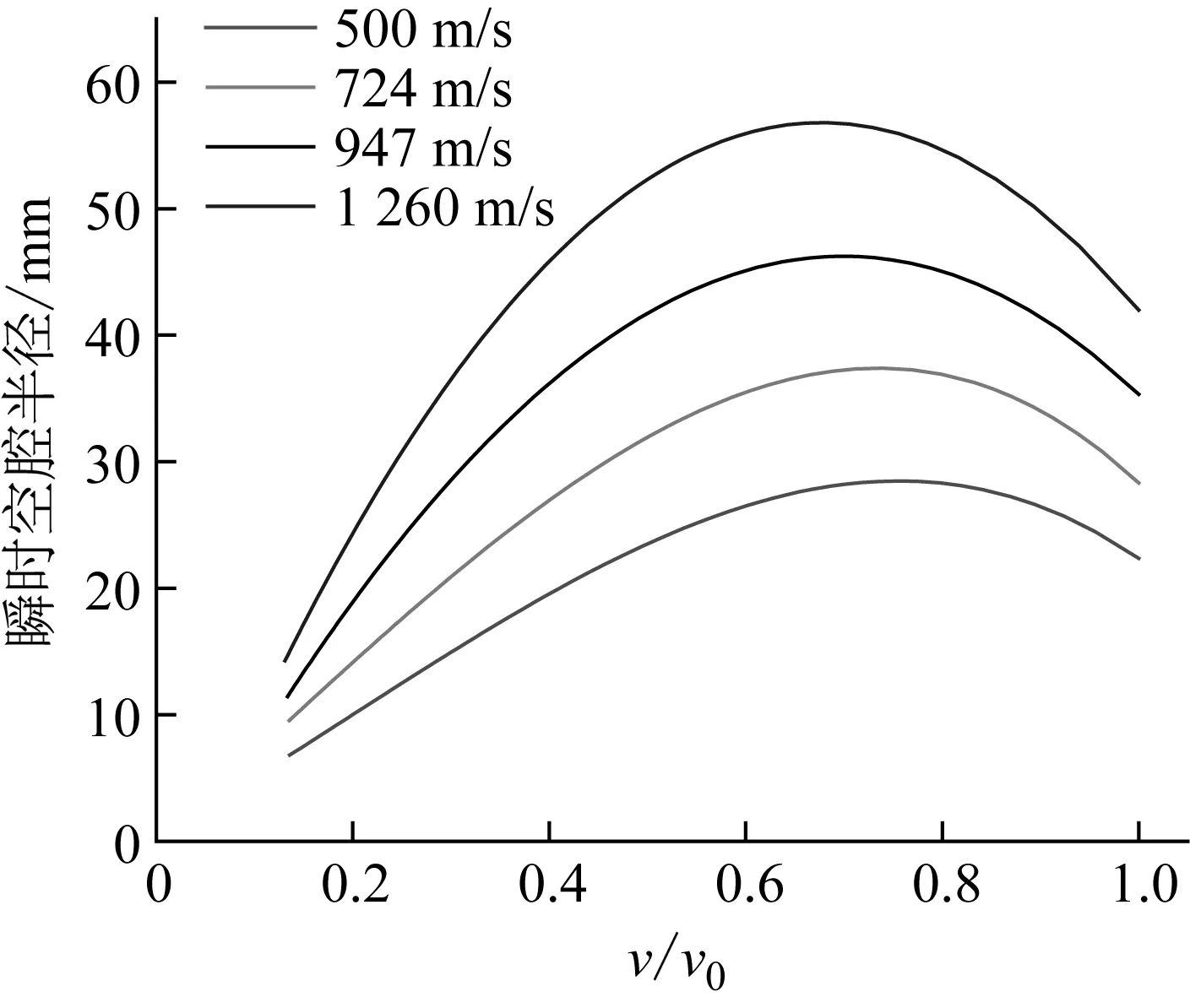
图8 Φ6 mm钢球不同着靶速度下计算结果Fig.8 Φ6 mm steel ball results at different velocities

3 遗传算法拟合公式

仿真结果中已经得到了钢球的直径、质量和着靶速度对瞬时空腔的影响规律，为了便捷地对瞬时空腔轮廓进行描述，一个简单直接的数学模型是人体易损性分析所需要的。人体损伤评估软件HVAssess[11]中将球形破片形成的瞬时空腔近似成圆锥，这与真实情况有一定的差异。刘苏苏等[12]通过参数化建模提取瞬时空腔的方式进行了改进，虽保证了瞬时空腔的可靠性，但无法用于随机破片的快速评估。因此，需要一个方便可靠的数学模型来描述损伤区域。

3.1 遗传算法

遗传算法(genetic algorithm,GA)是一种基于达尔文生物进化论中基因的遗传机理进行搜索的优化算法，其通过直接对被优化的结构对象进行编码，进而模拟人类种群中基因遗传过程产生的选择、交叉和变异现象[13]。在种群中，初始基因编码经过一定代数的遗传，子代在遗传过程中往往会产生更优秀的基因，即种群通过自然进化的行为来适应外部环境，而我们可以用调整目标函数的方式更改其所需适应的外部环境，从而筛选出最优秀的子代，达到结构最优化的目的。

在MATLAB软件中已经开发了GA工具包，按照上述遗传算法的基本设置进行输入，可以方便快捷地实现对最小值问题求解，这节省了在遗传算法编程上面消耗的时间，仅需对适应度函数进行描述。

3.2 速度衰减公式

Dziemian定律[14]常被用来计算射弹侵彻人体组织的速度衰减，它假设作用于侵彻弹丸的阻力是弹丸和目标靶性能的函数，表示成如下形式

(1)

式中：m为弹丸质量；v为弹丸速度；t为时间；ρ为组织材料密度；A为弹丸呈现面积；μ为紧挨弹丸的液体层黏度,l为紧挨弹丸的液体层厚度，φ=μ/l;S为组织强度;gD、gV、gS为无量纲系数。

考虑如下变换

(2)

可将式(1)写成

(3)

式中：σ为弹丸密度；a、b、c为常数；Q为等效长度，由Q=(m/σ)1/3得到。

通过求解式(3)，可得到经过侵彻深度Δx衰减后的速度公式

(4)

由于明胶与人体肌肉组织具有相似的性质，而式(4)的本质是动态阻力、黏性力和组织阻滞力对速度的函数，因此也应适用于明胶侵彻过程。基于遗传算法对16种工况的速度衰减曲线进行参数优化，在国际单位制下得到a，b和c取值如表4所示。拟合效果如图9所示。

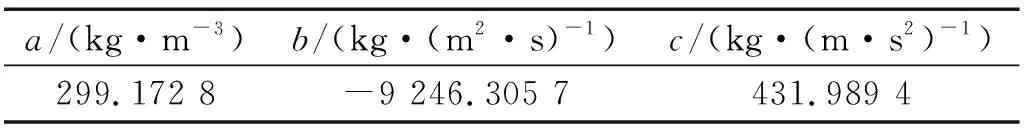
表4 速度衰减系数Tab.4 Velocity attenuation coefficients

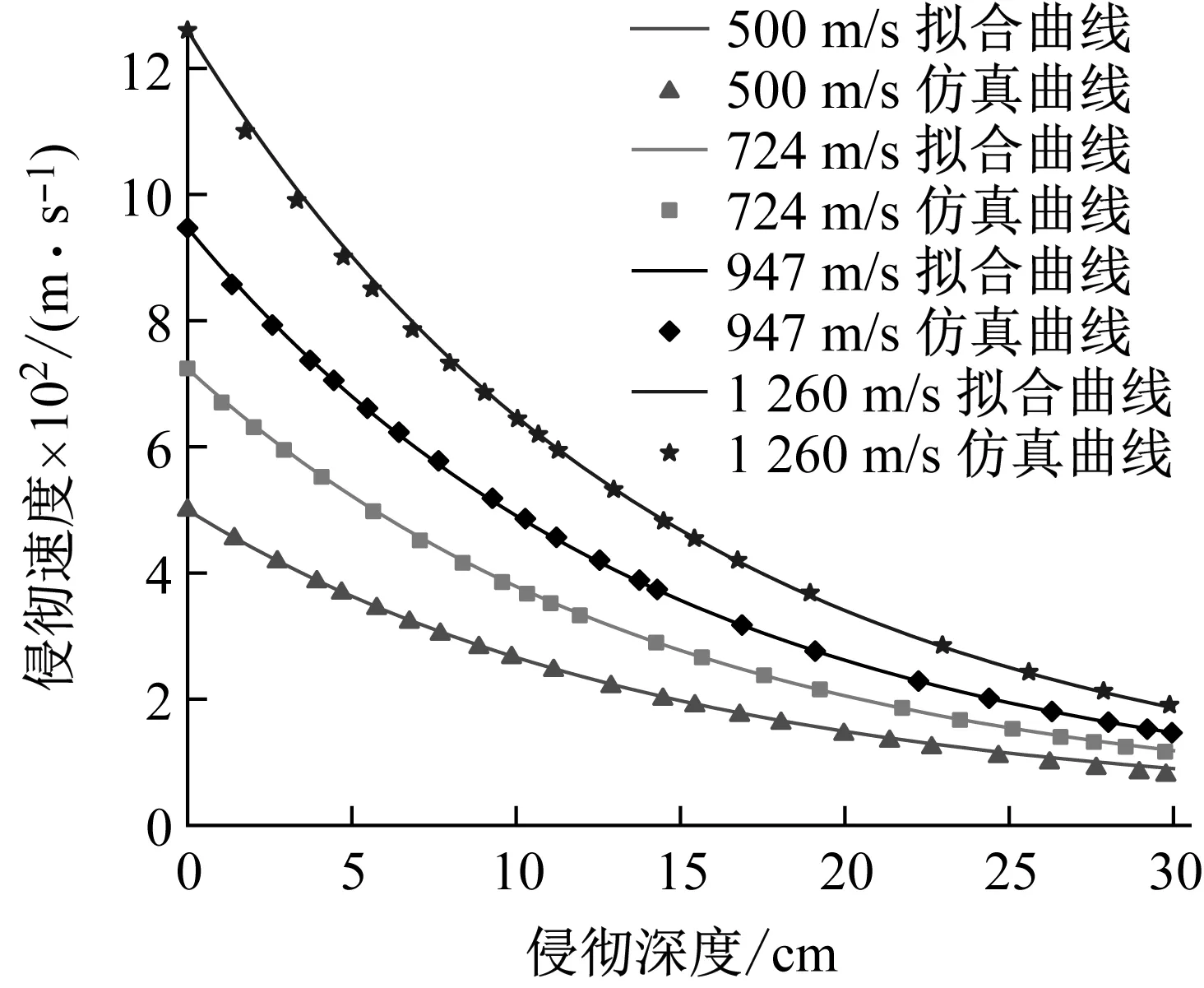
图9 Φ7 mm钢球速度衰减公式拟合结果Fig.9 Fitting results of velocity attenuation for Φ7 mm steel balls

3.3 瞬时空腔尺寸公式

前面分析了着靶速度和钢球直径对瞬时空腔尺寸的影响规律，发现瞬时空腔尺寸随速度衰减可分为两个阶段，即侵彻初期对应的“开坑段”和侵彻进行到一定程度后对应的“稳定段”。考虑到两个阶段不同的特性，应分别选取相应的瞬时空腔公式描述侵彻过程随侵彻速度衰减的瞬时空腔尺寸变化。

破片的呈现面积Ap是指侵彻过程中与靶标实际作用的破片截面积。呈现面积Ap的有效半径为

(5)

式中，γ为形状系数，球形破片的有效半径等于其自身半径，γ取为1.21。

对于瞬时空腔尺寸公式，考虑破片有效半径、瞬时空腔半径、侵彻速度、着靶速度、破片密度和明胶靶杨氏模量共6个影响因素，利用其无量纲组合建立瞬时空腔尺寸公式。

考虑到图8中“开坑段”的曲线形状更接近二次曲线，因此，侵彻初期瞬时空腔半径的函数形式为

(6)

其中α、β、λ、μ和η为无量纲系数，在国际单位制下，系数的具体取值如表5。

表5 式(6)的系数取值Tab.5 Values of the coefficients of Eq.(6)

进入到“稳定段”后的瞬时空腔尺寸与速度衰减程度基本呈线性，且入射速度影响其斜率，因此，侵彻进行到一定程度后瞬时空腔半径的函数形式为

(7)

其中ζ、ε和κ为无量纲系数，在国际单位制下，系数的具体取值如表6。

表6 式(7)的系数取值Tab.6 Values of the coefficients of Eq.(7)

通过对式(6)和式(7)分别拟合得到了两段瞬时空腔半径随侵彻速度衰减的拟合曲线，将两段曲线的交点作为两段侵彻过程的划分点，从而可以得到整体的拟合曲线，拟合结果如图10所示。

由于某些工况下侵彻初期的曲线与稳定段曲线没有交点，为了对瞬时空腔尺寸有较好的描述，需要选取适当的分割点并通过一定的过渡段将两段曲线连接，如图10中1 260 m/s拟合曲线中的过渡段为一条直线。

图10 Φ6 mm钢球对瞬时空腔尺寸公式的拟合结果Fig.10 Fitting results of temporary cavity size for Φ6 mm steel balls

3.4 瞬时空腔模型

结合3.2和3.3节得到的速度衰减公式和瞬时空腔尺寸公式，本文得到了一个计算瞬时空腔的简易模型，可以对给定直径、密度和着靶速度的球形破片较为快速地计算出其侵彻形成的瞬时空腔。

该简易模型的计算流程可简述为：第1步，将考虑的侵彻深度范围划分成一个个较小的间隔；第2步，根据已知破片条件，由3.2节中式(4)可计算得到破片侵彻一个间隔距离后的衰减速度；第3步，将破片的初始信息和衰减后的侵彻速度作为输入，由3.3节中式(6)和式(7)分别得到两个瞬时空腔半径，通过判断当前侵彻过程所处阶段确定其中一个半径表征该间隔上的瞬时空腔尺寸；第4步，重复第2、3步计算直至最后一个间隔；最终，经过上述四步的计算，得到了各间隔对应的瞬时空腔半径，这些半径实际上描述了破片侵彻明胶造成的瞬时空腔轮廓。

图11为利用该模型计算得到的结果与LS-DYNA数值模拟结果的对比图，可以发现本文建立的简易模型与仿真软件的结果吻合度较好，而在侵彻初始阶段的明胶受挤压和回弹作用在仿真中产生了锯齿状的空腔边界形状，但模型计算结果与锯齿外沿相贴，能够较为准确地描述空腔区域轮廓。通过16种拟合工况之外的仿真结果和计算结果的比对，也验证了此模型的有效性。

图11 初速800 m/s的Φ6.5 mm钢球最大瞬时空腔模型计算结果Fig.11 Calculation results of the maximum temporary cavity model for Φ6.5 mm at a velocity of 800 m/s

4 结 论

本文基于非线性显式计算有限元软件LS-DYNA，对不同直径和着靶速度的钢球侵彻明胶过程进行了数值模拟，通过文献中的试验结果验证了二维轴对称模型的可靠性。经整理分析得到了球形破片直径和着靶速度对侵彻速度衰减和瞬时空腔尺寸的影响规律，发现高速度、大直径的球形破片具有更强的穿透能力和更大的空腔尺寸，而高速度、小尺寸的球形破片穿透相同厚度明胶靶标的速度衰减更严重。

基于仿真结果，利用遗传算法对速度衰减公式和瞬时空腔尺寸公式进行拟合，得到了简易瞬时空腔模型。通过与仿真结果提取的二维瞬时空腔轮廓进行对比，验证了该模型的有效性。该模型极大缩短了计算瞬时空腔的时间，可提高相应毁伤评估的效率。