黄土沉积过程及微结构模型的非连续变形分析*

张 杰 李 萍 李同录 张常亮 乔志甜 李 强 沈 伟

(①长安大学地质工程与测绘学院， 西安 710064， 中国) (②黄土高原水循环与地质环境教育部野外观测研究站， 正宁 745399， 中国) (③博洛尼亚大学， 生物、地球与环境科学系， 博洛尼亚 67-40126， 意大利)

0 引 言

黄土是一种成分均一、多孔隙、水敏性强的风力搬运堆积物，具有显著的结构性(朱兴华等， 2017)，其变形破坏特征实际是微观结构发生破坏的宏观表现，探究黄土微观结构的破坏行为有利于揭示黄土宏观变形破坏的根源(袁志辉等， 2018)。

黄土的微观结构是组成黄土的原始物质在沉积后，于特定的自然环境下，经过一系列物理化学作用形成的(方祥位等， 2013)。探究黄土微观结构的变化，需首先建立黄土原始物质沉积后形成的初始结构。目前建立黄土微观结构主要有两种方法，一种是数值模拟法，另一种是图像处理法。数值模拟法通过Monte Carlo等方法在一定空间内填充土体颗粒，从而形成黄土的微观结构。如Rogers et al. (1994)通过在一定范围内赋予颗粒随机角度和位置的办法建立了黄土的初始结构，并研究了颗粒之间的胶结作用，认为前期胶结作用是黄土后期产生湿陷的重要原因； Assallay et al. (1997)在假定颗粒水平、角度不变、胶结力与颗粒重力比为1，即颗粒在接触瞬间便粘合的前提下，使用Monte Carlo法随机充填并构建了黄土的二维初始结构； Dibben et al. (1998a，1998b)进一步拓展了Assallay et al. (1997)的方法，假定了一个临界胶结力，当该胶结力大于重力时，两颗粒粘合，否则颗粒移动，据此建立了黄土的初始结构，并且研究了颗粒的大小和形状对结构的影响。图像处理法则通过扫描电镜以及断面扫描(CT)等技术对黄土进行断面扫描获得黄土的微观结构图像，然后统计求解相关结构参数，基于参数控制建立黄土微观结构。如陈开圣等(2009)基于数字图像处理技术，定性和定量分析了不同压实度下黄土的微结构特征； 谷天峰等(2011)基于扫描电镜图像分析了Q3黄土的微结构变化； 陈阳等(2015)基于扫描电镜图像和光学显微镜图像分析了黄土湿陷前后微结构的变化特征； Liu et al. (2015)基于扫描电镜图像建立了一种4层结构的黄土概念微结构模型； Li et al. (2019)基于扫描电镜图像建立了不同压力和含水率下的微结构模型。综上所述，数值模拟法在构建黄土微观结构时，假定条件过于理想，没有考虑黄土在形成初始结构时颗粒之间力的作用； 图像处理法建立的结构模型只能做统计分析，无法进行力学模拟，不利于进一步分析结构变化。

基于以上研究，本文提出了一种模拟黄土沉积过程并构建黄土初始结构的方法，即先利用Monte Carlo法生成沉积前的黄土颗粒群，然后引入非连续变形分析方法(DDA)模拟黄土的沉积过程，该方法能够模拟颗粒下落过程中的相互碰撞及摩擦，由此建立黄土的初始结构模型。最后，利用建立的结构模型模拟了黄土的压缩试验，通过与相同条件下物理模型试验结果的对比，初步表明该方法是可行的。

1 基于Monte Carlo法的黄土颗粒群生成

1.1 黄土颗粒形态的确定

黄土颗粒的形状是其结构的要素之一，它是决定黄土结构排列并引起湿陷的重要因素(Smalley et al.，2017)。Krinsley et al. (1973)认为微小的沉积石英颗粒是一种扁平状的颗粒。在此基础上，Rogers et al. (1993)应用Monte Carlo抽样统计分析了黄土颗粒形状和大小的分布模式，表明黄土中的石英颗粒主要是一种粒径为30μm的扁平状颗粒，且其长、宽、高之比约为8︰5︰2，如图 1a所示(Domokos， 2010； Howarth， 2010； Assadi Langroudi et al.， 2014， 2018)。Dibben et al. (1998)研究了二维平面上颗粒的形状和大小对黄土结构的影响，结果表明在二维平面上用长宽比为3︰1的矩形颗粒代表石英颗粒较为合理。本文根据Dibben et al. (1998)的研究结论，在模拟二维平面上的黄土沉积过程时，采用3︰1的矩形颗粒代表以石英、长石为主的粗骨架颗粒(图 1b)。

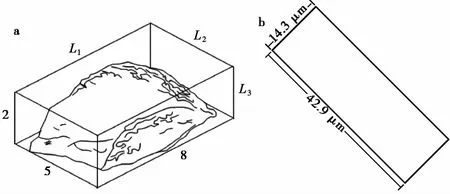
图 1 黄土颗粒的形状Fig. 1 The shape of loess particles

为了确定黄土颗粒的最优势粒径，统计了400组陕西省自陕北到关中马兰黄土的粒度分析结果，统计出其平均粒径d50的频率分布，总共获得400个平粒粒径，作出平均粒径频率分布直方图(图 2)。可以看出黄土的粒径主要集中于26～30μm，因此选取中位数28μm作为黄土的优势粒径。采用等效面积粒径法确定二维平面上颗粒的粒径，使矩形颗粒的面积与直径为28μm的圆面积相等，可得矩形石英颗粒的等效长度为42.9μm，等效宽度为14.3μm。

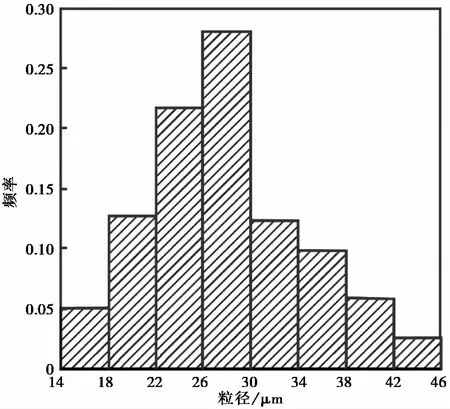
图 2 黄土颗粒平均粒径频率分布Fig. 2 Frequency distribution of average particle size of loess

实际上黄土颗粒的形状和大小各异，若按实际形状和大小模拟，计算将变得十分复杂，目前的计算能力基本难以实现。本文先注重于算法的探讨，因此基于上述统计结果，将黄土颗粒按大小和形状相同处理。

1.2 黄土颗粒群的生成

利用选定大小和形状的二维颗粒，使用Monte Carlo法在预先设置的区域内，随机生成沉积前的黄土颗粒群，本文给定一1.0mm×0.7mm的区域。具体步骤为：

(1)在已确定的垂直立面上的一个方形区域中，建立直角坐标系，水平为x坐标，垂直为y坐标。

(2)使用Monte Carlo法，抽取3个随机数，将其分别换算为颗粒在指定区域的(x，y)值，及颗粒长轴与x轴的夹角α， 0≤α≤360°。

(3)只要新颗粒与已有颗粒发生一定的重叠，认为该颗粒生成失败，同时赋予该颗粒一个新坐标。

(4)由于颗粒的位置和方向是随机的，随着颗粒增多，新颗粒和已有颗粒可能发生重叠，当发生重叠时，放弃该颗粒，重新抽样。

(5)经反复测试，当颗粒连续15～20次与已有颗粒重叠时，颗粒已经均匀地填满指定空间，则结束运算。

利用该方法生成的黄土颗粒群如图 3所示。

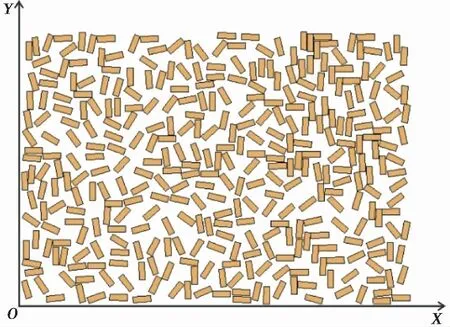
图 3 利用Monte Carlo法生成的黄土颗粒群Fig. 3 Loess particle group generated by Monte Carlo method

图 4 黄土沉积DDA初始数值模型Fig. 4 Initial numerical model of DDA in loess deposition

2 基于DDA的颗粒群沉积过程模拟

首先建立用于存储颗粒的模型盒，模型盒内部尺寸为0.7mm×0.5mm。利用Monte Carlo法随机生成颗粒群置于模型盒上方，如图 4所示。

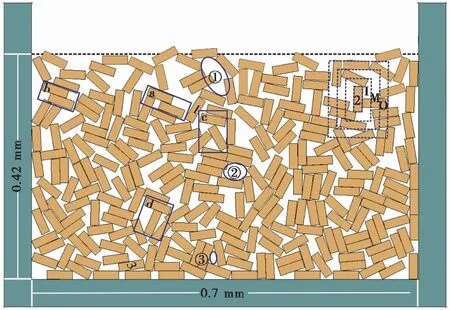
图 5 初始黄土微观结构模型Fig. 5 Initial loess microstructure model a. 台阶结构， b. 堆叠结构， c. 点接触结构， d. T型结构； ①. 大孔隙， ②. 中孔隙， ③. 小孔隙

由于黄土颗粒微小，在实际下落过程中，受到重力与空气阻力的共同作用，并非加速下落，而是时快时慢，运动轨迹也非垂线，但其速度和轨迹对模型影响不大，因此在建模时不考虑速度和轨迹的影响，将颗粒的初速度设置为0。由于黄土颗粒的成分主要是长石和石英，类似于花岗岩(谢星等， 2013)，因此颗粒的弹性模量、泊松比参考花岗岩的参数取值，密度可通过室内试验获得，松散状态下黄土的内摩擦角与其休止角相等，可取休止角。黄土颗粒及土样盒的物理力学参数如表 1。相对于土颗粒，模型盒为刚体，因此模拟时使其弹性模量远大于土体。

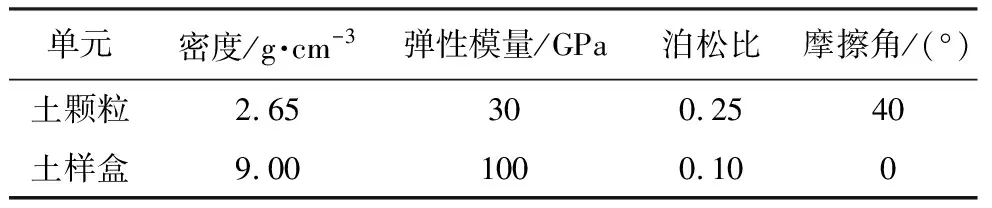
表 1 模型物理力学参数Table 1 Physical and mechanical parameters of model

初始数值模型建立后，同时释放所有颗粒，颗粒在下落中会相互碰撞和摩擦，颗粒群在重力作用下下降并在模型盒中堆积。最终堆积稳定，形成的黄土初始微观结构模型如图 5所示。可以看出，生成的模型中，底部较密实，向上变疏松，中上部有架空的大孔隙，和实际沉积的黄土结构有相似性。

由图 5生成的初始黄土微观结构模型可以看出，颗粒间主要有4种接触结构类型，分别为：a. 台阶结构(staircase)(Smalley et al.，1969)、b. 堆叠结构(stack)、c. 点接触结构(point contact)(Assallay et al.，1997)、d. T型结构。其中，台阶结构(staircase)是黄土中最基本的一种接触结构，在黄土中大量存在。堆叠结构(stack)中两个颗粒之间的接触面积比台阶结构(staircase)大，当两颗粒之间的接触面积大于50%时为堆叠结构，小于50%时为台阶结构，因此堆叠结构(stack)比台阶结构(staircase)稳定。点接触结构非常不稳定，但是在初始结构中这种点接触数量居多，在上覆土层压力作用下，这种接触结构首先被破坏，这种不稳定的点接触是评价黄土塌陷的关键。T型结构也是一种不稳定的结构，在压缩过程中，上部颗粒和下部颗粒均有可能倒塌，形成其他更稳定的接触结构，在以往学者构建的模型中并没有发现这种结构，实际黄土中可见到这种结构，如图 6所示(Milodowski et al., 2015)。以上颗粒接触结构往往不是单独存在的，会与其他结构相互组合，组成更复杂的接触结构。

图 6 黄土中的T型接触结构Fig. 6 T-type contact structure in loess

在图 5中，可以明显看到大、中、小3种类型的孔隙。其中，大孔隙半径>0.016mm，主要由骨架颗粒相互支撑形成，孔径大于骨架颗粒粒径，这类孔隙较多地存在于黄土的初始结构中，黄土湿陷时，这类孔隙首先破坏，颗粒可以掉落其中，变为中孔隙或小孔隙。中孔隙半径为0.004～0.016mm，主要由黄土颗粒相互穿插嵌套形成，孔径比骨架颗粒粒径小，在黄土受荷时，支架颗粒可以移动和转动，使得这类孔隙变小。小孔隙的孔径远远小于骨架颗粒的粒径，为0.001～0.004mm，体积小，数量多，呈缝隙状或者似三角形，这类孔隙十分稳定，不足以变形。

在图 5所示模型的上方画一条水平线，计算出初始结构的孔隙比为0.60。该模型在二维平面上建立，所生成的结构为二维结构，计算所得孔隙比与三维空间的孔隙比不同，二维要小于三维(黄磊等， 2016)。利用Hoomans et al. (1996)提出的等粒径颗粒二维孔隙与三维孔隙的转化式(1)，可实现二维与三维的转化。经计算，所生成的初始结构三维孔隙比为1.36。

(1)

式中：n2D、n3D分别为土体的二维、三维孔隙率。

3 压缩试验模拟

利用DDA的算法，通过在受荷位置施加点荷载的方式给生成的微结构模型结构加载，通过指定测量点的位移变化确定变形参数并判定是否稳定。通常当测量点的位移在两个时间步的差值为0.0001时，可认为在该级荷载下达到稳定，施加下一级的荷载(郭龙骁等， 2017)。对图 5中的黄土初始结构先施加5kPa的正应力压缩，变形稳定后黄土的亚稳态(metastable)结构二维孔隙比为0.49(图 7)，对应的三维孔隙比为1.13。在此基础上，设置了4个测量点和荷载点，对其施加10kPa、25kPa、50kPa、100kPa、200kPa、400kPa、800kPa的荷载进行模拟。

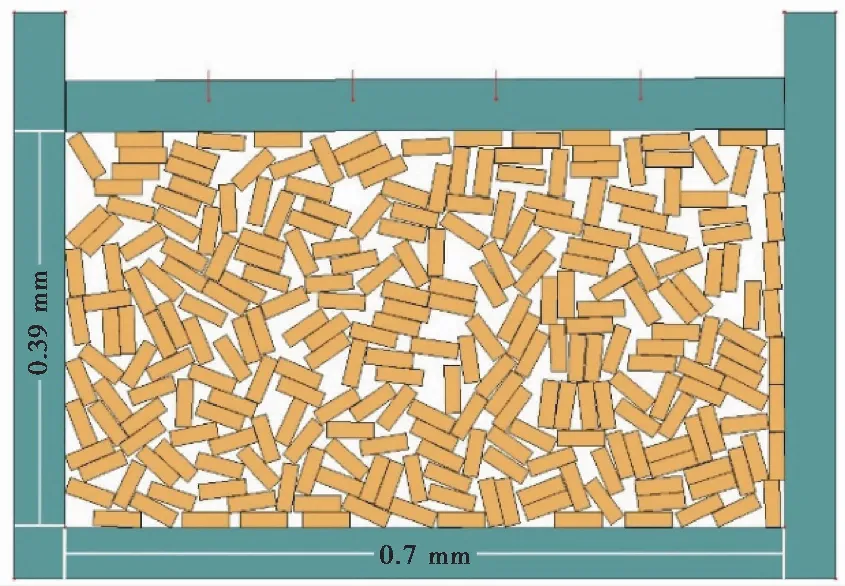
图 7 黄土的亚稳态结构Fig. 7 Metastable structure of loess

当荷载小于50kPa时，由于荷载较小，结构变化不太明显。故在这里只展示荷载大于50kPa的压缩结果，如图 8所示。从图中可以明显地看出，随着荷载的增加，架空结构和大孔隙首先破坏，部分土颗粒进入大孔隙中，孔隙变小，当加载到800kPa时，大部分大孔隙基本闭合。

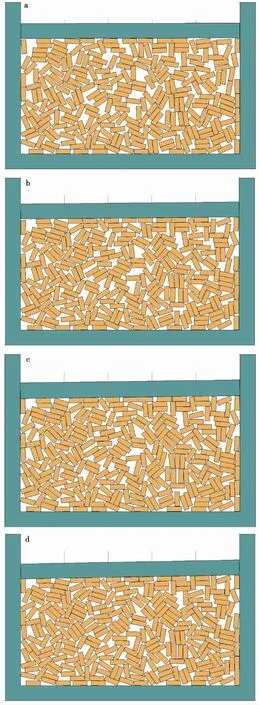
图 8 各级荷载稳定后的模型Fig. 8 Model after load stabilization at each level a. 加载100kPa； b. 加载200kPa； c. 加载400kPa； d. 加载800kPa

图9为黄土模型孔隙比转化为三维后的e-lgp曲线，可以看出，该曲线和物理试验获得的e-lgp曲线非常相似。压力为100kPa之前曲线平缓，其后曲线陡降，也与图 5中大孔隙和架空结构的破坏相对应。

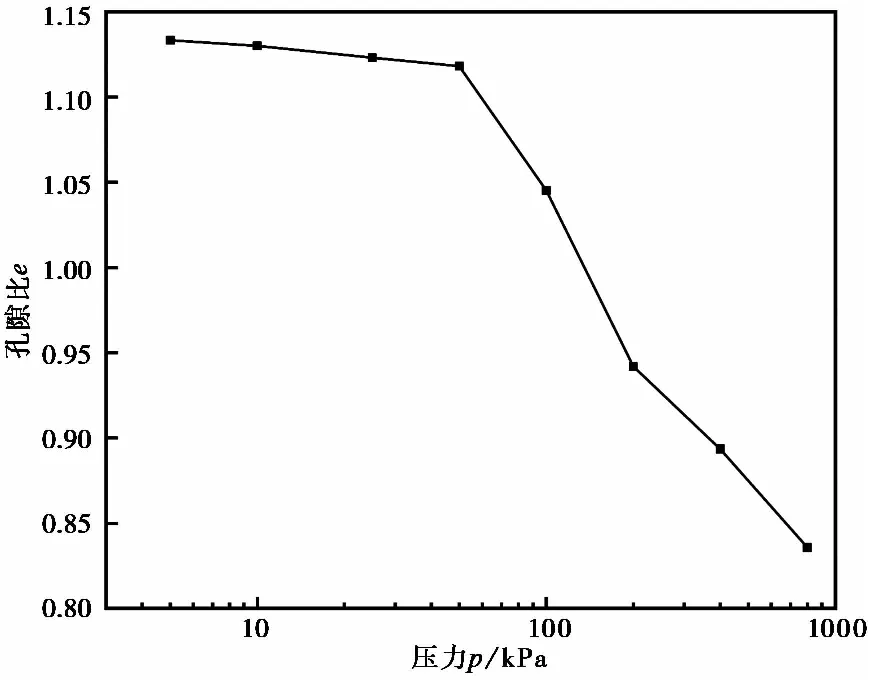
图 9 数值模型压缩曲线Fig. 9 Compression curve of the numerical model

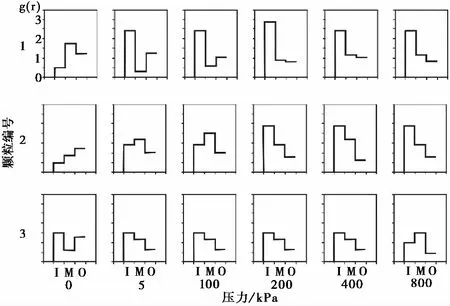
图 10 选定颗粒的径向分布函数Fig. 10 The radial distribution function of selected particle

为了从微观角度研究黄土初始结构模型在压缩过程中的变化，引入径向分布函数。径向分布函数反映了以任意颗粒为中心，其周围颗粒的对称径向分布状态。在所生成的黄土模型中选择某一颗粒，以该颗粒为中心画出3个同心矩形区域，分别命名为内侧(I)、中部(M)、外侧(O)，如图 5所示。每个区域的径向分布函数的计算方法如式(2)。

g(r)=ρ(r)/ρa

(2)

式中：ρ(r)为粒子径向分布的数密度；ρa为整个系统的平均粒子数密度。

在所建立初始模型中选择3个不同部位的颗粒，颗粒1、2、3分别为大、中、小3类孔隙附近的颗粒，在不同荷载下，其径向分布函数如图 10所示。

从图 10可以看出图 5的黄土初始结构极为不稳定，在5kPa正应力作用下，颗粒1内侧区域(I)的径向分布密度显著增加，中间区域(M)值显著减少，说明中间区域(M)的颗粒滑向了内侧区域(I)，使得最内侧区域变得拥挤，在200kPa时颗粒1的内侧区域(I)值达到最大，此后颗粒内侧区域(I)值不再变大，说明此时颗粒1内侧达到最拥挤状态，随后中间区域(M)值开始变大，并且内侧区域(I)值出现减少，说明其内侧区域(I)某些颗粒发生了侧移，移向了中间区域(M)。颗粒2在5kPa的正应力作用下，内侧区域(I)与中间区域(M)值均增加，但没有颗粒1显著，外侧区域(O)值减小，说明外侧区域(O)颗粒滑向了内侧区域(I)和中间区域(M)。颗粒3在压缩过程中径向分布密度基本不变。综上所述，黄土在压缩过程中大孔隙和架空结构会首先被破坏，且破坏程度最大，而小孔隙基本不会变化。

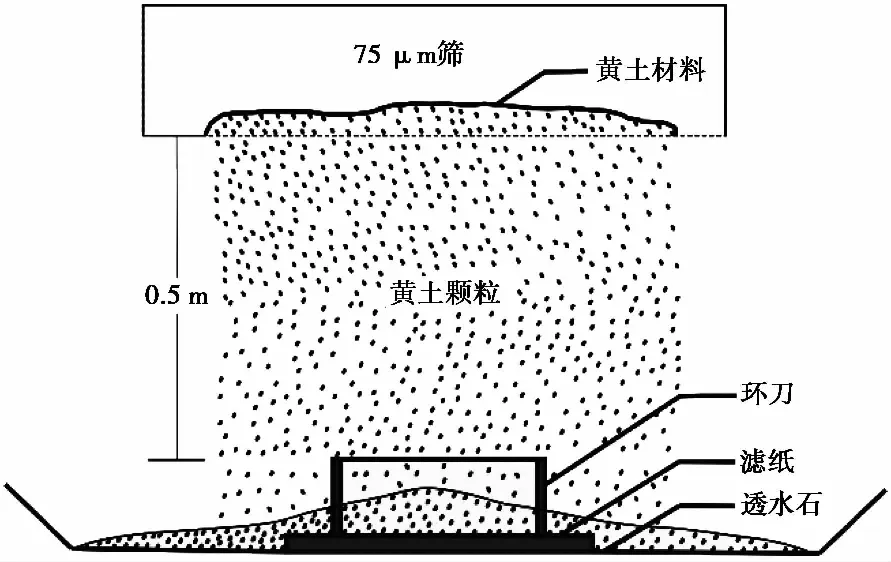
图 11 黄土沉积过程试验方案示意图Fig. 11 Schematic diagram of test scheme for loess deposition process

4 与物理模型试验的对比

4.1 试验设计

数值模拟只有在与天然物质的行为相匹配的情况下才有用，因此为了验证数值模型的可行性，本文设计了一个物理模型试验，如图 11所示。土样取自陕西咸阳黄土塬北缘剖面上的L5层黄土。先将土样碾碎、烘干，测得其比重为2.71。将试样置于75μm的筛中，在固结仪应力盒正上方一定高度轻轻晃动筛子，将土粒筛落在压力盒中，待装满压力盒时停止。本试验将筛子水平置于压力盒上方大约0.5m的位置。

待样品装满压力盒后，仔细平整表面，尽量避免扰动，此时测得样品的孔隙比为1.83。接着在样品上轻轻地放置一块透水石并盖好盖子。固结仪的盖子和透水石可提供1kPa的正应力，将正应力增加到5kPa，此时样品形成了亚稳态(metastable)结构，孔隙比为1.44。随后调整样品，往压力盒中筛入更多的样品，并轻微地压缩，制取两组孔隙比约为1.14(与数值模拟形成的孔隙比大致相等)的样品，将样品放在一维固结仪中依次用5kPa、10kPa、25kPa、100kPa、200kPa、400kPa、800kPa的正应力压缩。

4.2 结果对比与分析

绘制物理试验与数值模拟的压缩曲线e-lgp如图 12所示，可以看出，曲线的趋势相同，但两者之间仍然存在一定的偏差，并且数值模拟形成的初始结构的孔隙比与模型试验土样的孔隙比存在一定差距，考虑主要是由于实际黄土颗粒的大小和形状各异，而本文为了简化模型用一种理想化的颗粒代替。后续将在考虑该因素的基础上开展进一步研究。

图 12 数值模拟与实际试验对比Fig. 12 Comparison between numerical simulation and actual experiment

5 结 论

本文提出模拟黄土沉积过程和构建黄土初始结构的方法，并对黄土的压缩试验进行模拟，得出以下结论：

(1)生成黄土的初始结构，对该结构中的孔隙及接触结构进行分析，发现所生成结构中主要存在大、中、小3种孔隙； 存在台阶(staircase)、堆叠(stack)、点接触(point contact)、T型4类主要的接触结构。

(2)模拟黄土的压缩试验，得到了压缩曲线，并选取特定颗粒作出了径向分布函数，从微观角度说明黄土在压缩过程中架空结构和大孔隙首先会被破坏，而小孔隙基本不会变化。

(3)设计物理模型试验，与数值模拟结果进行对比，两种压缩曲线趋势大致相同，表明本文方法是可行性，为黄土微观力学的进一步研究提供了基础。