节理迹线中点密度修正方法的探讨*

刘 健 王 驹 陈 亮 云 龙 王春萍

(核工业北京地质研究院环境工程研究所， 北京 100029，中国)

0 引 言

节理在岩体中普遍存在，其密度、尺寸和产状等特征信息，是进行地下工程岩体质量评价的重要指标(Bieniawski， 1973； 韩振华等， 2019)。露头调查是获得节理特征信息的主要手段之一。但是，露头调查揭露的节理迹线分布信息通常含有以下4种误差(Zhang et al.， 1998)：

(1)截短误差，即由于野外调查精度的限制，通常需要忽略某一长度阈值之下的节理迹线。截短误差使得节理密度被低估，使得节理迹长被高估。

(2)截长误差，即由于测窗或露头范围的尺寸限制，某些迹线起始点或终止点的位置无法确定。截长误差通常使得节理密度被高估，使得节理迹长被低估。

(3)尺寸误差，即测窗或露头更容易与大节理相交、测线更容易与长迹线相交。尺寸误差通常使得节理迹线密度被低估，节理迹长被高估。

(4)角度误差，即节理面与测窗或测线的夹角越大，则相交概率越大； 反之，则相交概率越小。角度误差使得与测窗或测线夹角大的节理的密度被高估，使得与测窗或测线夹角小的节理的密度被低估。

当野外测量的最小迹长阈值远小于平均迹长和地下洞室截面尺寸时，可以忽略截短误差的影响(Zhang et al.， 1998)。同时，随着无人机摄影以及三维点云处理等技术的引入，使得迹长测量精度接近厘米级，大大降低了截短误差的影响(赵明宇等， 2018； 张恺等， 2019)。在此前提条件下，对于满足“三维空间条件下中心点服从泊松分布”假设(Lanney， 1978)的平行、近平行或者分组平行节理，迹长信息主要受到上述截长和尺寸误差的影响，密度信息主要受到上述截长、尺寸和角度误差的影响(Song， 2006)。针对迹长信息的误差修正，从20世纪70年代开始国内外学者已经开展了大量的研究(陈剑平等， 1996； Cruden， 1977； Pahl， 1981； Wu et al.，2011)，此处不作讨论。本文重点分析节理密度的误差修正方法。

为修正截长和尺寸误差对节理密度的影响，Mauldon(1998)通过关联点分析，推导获得了任意形状凸面测窗中节理迹线中点密度的计算公式。Zhang et al.(1998)通过对Pahl(1981)以及Kulatilake et al.(1984)方法的拓展，推导出了圆形测窗中节理迹线数量、平均长度和迹线中点密度的关联关系。杨春和等(2006)根据上述关联关系推导了圆形测窗条件下节理迹线中点密度的计算公式，与Mauldon(1998)提出的计算公式一致。此外，Song(2006)将测窗面积倒数作为权重系数，进一步将Mauldon(1998)计算方法推广至多个不平行面组成的测窗中。但是，上述方法均没有考虑角度误差的影响。

为修正角度误差，Terzaghi(1965)最早提出了利用节理面与测线或测窗夹角正弦倒数进行修正的思路。根据上述原理，Palmström(1995)认为可以将每条节理与测线或测窗的夹角正弦倒数作为节理出现频率的权重系数，并提出了修正节理密度指标wJd。Sonmez et al. (2004)指出了指标wJd对测窗长度的敏感性，并提出了利用方形测窗计算指标wJd的方案。Nefeslioglu et al. (2006)在大理岩采石场块体分析中使用了指标wJd，发现其与节理密集度具有很好的对应性。刘明等(2016)推导了倾斜测窗上指标wJd的计算公式。但是，上述研究成果并没有完全解决指标wJd对测窗尺寸敏感等问题。

上述研究中鲜有同时修正截长、尺寸和角度误差的计算方法。因此，通过融合上述修正方法，本文提出了一种可以同时修正截长、尺寸和角度误差的节理迹线中点密度计算方法，继而利用算例测试和验证了新方法的有效性，最后实现了岩体露头节理数据的实例分析。

1 基本原理及改进方法

Mauldon(1998)基于关联点分析提出了截长和尺寸误差修正方法，适用于任意凸面测窗，是目前最为常用的节理迹线中点密度计算方法之一。而目前的角度误差修正方法则主要是Palmström(1995)基于Terzaghi(1965)修正原理提出的计算方法。本节首先介绍上述修正方法，继而提出可以同时修正截长、尺寸和角度误差的节理迹线中点密度计算方法。

1.1 截长和尺寸误差修正方法

Mauldon(1998)通过关联点分析，提出了可以修正截长和尺寸误差的节理迹线中点密度计算方法：

(1)

式中：d为节理迹线中点密度；A为测窗面积；N为测窗内节理迹线总数目；Nt为上下端点均不可见的迹线的数目，Nc为上下端点均可见的迹线的数目(图 1)。上述公式仅假定迹线在二维平面上均匀分布，只需要输入节理迹长及其位置信息； 适用于任意形状的凸面测窗； 对测窗面积无明确要求，建议通过改变测窗面积进行试算，在测窗面积v.s. 密度曲线上寻找平稳水平段，继而确定最终的密度计算结果。上述公式实际上忽略了上下端均不可见的迹线，同时将仅有一个端点可见的迹线的频数乘以权重系数0.5，从而实现了截长和尺寸误差的修正。

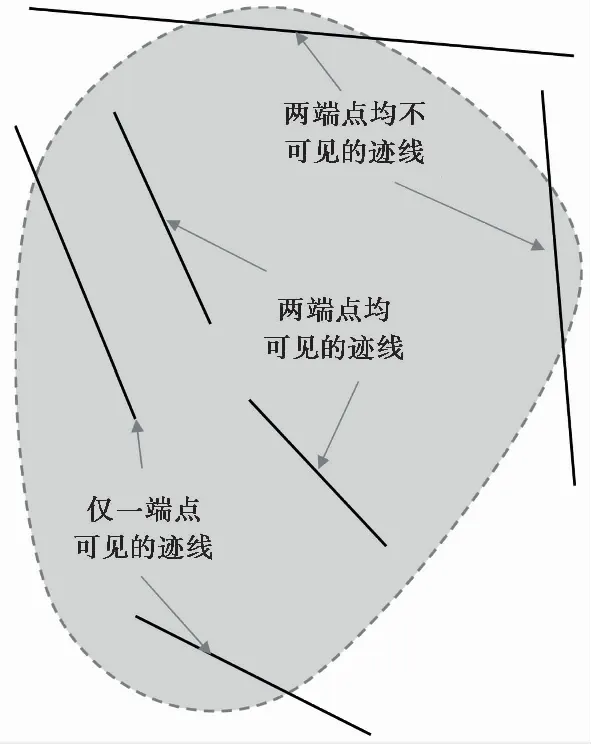
图 1 凸面测窗与节理迹线示意图Fig. 1 Sketch of joint traces and convex survey window

上述计算方法不需要预先进行节理优势组划分，也不需要预估节理迹线的分布函数，易于实际应用。杨春和等(2006)和雷光伟等(2016)利用上述计算方法分析了迹线中点密度和到断裂带距离的相关关系，实现了花岗岩岩体中断裂影响带的识别。但是，上述计算方法没有考虑露头面与节理面夹角变化而引起的角度误差。

1.2 角度误差修正方法

Palmström(1995)将每条节理与岩体露头面的夹角的正弦倒数作为节理出现频率的权重系数，提出了可以修正角度误差的密度指标wJd。为了减小指标wJd对测窗面积的敏感性，刘健等(2018)将指标wJd计算公式中的面积平方根调整为面积：

(2)

式中：wJd为修正后的节理迹线密度；A为测窗面积；N为测窗内节理迹线总数目；δ为节理面与露头面的夹角。上述公式需要输入节理产状和露头方位信息，适用于任意形状的测窗，对测窗面积无明确要求。

上述计算方法同样不需要预先进行节理优势组划分，也不需要预估节理迹线的分布函数，易于实际应用。算例表明，指标wJd对露头的方位变化不敏感，并且其取值与节理体密度具有良好的线性对应关系； 但是，在较小测窗半径条件下，修正后的指标wJd取值仍存在较大幅度的波动(刘健等， 2018)。这说明指标wJd可以修正角度误差，但是仍然受到测窗尺寸的影响。

1.3 截长、尺寸和角度误差联合修正方法

将1.2节使用的“节理面与露头面的夹角的正弦倒数”作为加权系数，带入到1.1节的计算公式中，继而提出了同时修正截长、尺寸和角度误差的计算公式：

(3)

式中：d为迹线中点密度；A为测窗面积；N为测窗内迹线总数目；Nt为上下端点均不可见的迹线的数目；Nc为上下端点均可见的迹线的数目；δ为节理面与露头面的夹角。上述公式的适用条件与式(1)一致，但是需要附加输入露头方位和节理产状信息。

式(3)是式(1)和式(2)的融合，可以同时完成截长、尺寸和角度误差的修正。此外，式(3)同样可以继承式(1)和式(2)的优点：不需要预先进行节理优势组划分，也不需要预估节理迹线的分布函数，易于实际应用。

2 算例验证

借助三维节理网络建模技术，模拟不同方位的岩体露头，布置不同尺寸和形状的测窗，分析了截长、尺寸和角度误差的影响，测试了新算法的性能。

2.1 测试模型构建

测试模型的节理产状和尺寸信息参照我国高放废物处置旧井预选区十月井断裂附近的节理分布信息(表 1和表 2)(刘健等， 2018)。其中，产状服从Elliptical-Fisher分布，其概率密度分布函数为(Golder Associates Inc.，2018)：

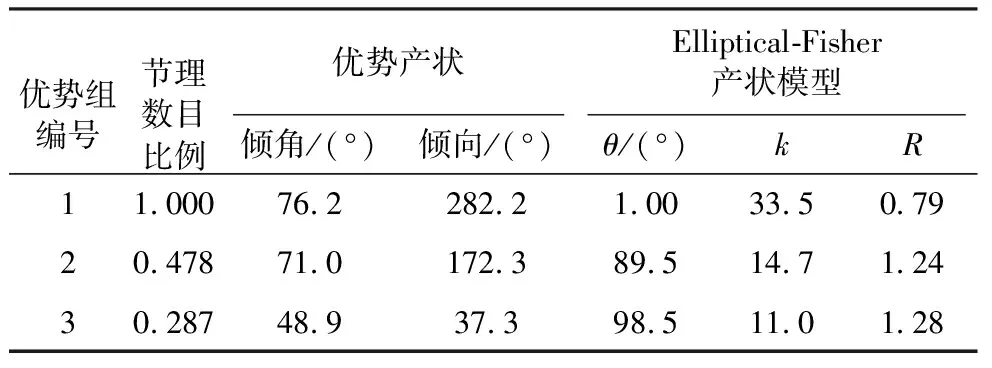
表 1 节理产状分布模型和参数(刘健等， 2018)Table 1 Distribution law and parameters of joint occurrence

表 2 节理直径分布模型和参数(刘健等， 2018)Table 2 Distribution law and parameters of joint diameter

f(φ，β|k，R，θ)

(4)

式中：φ和β为将Schmidt投影球z轴旋转至优势产状方向后计算获得的节理的相对倾角和倾向；k为离散系数，反映产状数据的离散程度；R为椭圆长短轴系数，反映产状数据在两个相互垂直方向上的密度分布差异；θ为旋转后的Schmidt投影球的正北方向相对于原有正北方向的旋转角。

根据“三维空间条件下中心点服从泊松分布”的圆盘节理假设(Lanney， 1978)，利用蒙特卡洛随机抽样技术构建100×100×100m3范围的三维节理网络模型(图 2)。优势组-1的节理体密度设定为0.05m-3，优势组-2和优势组-3的体密度按照表 1中相对于优势组-1的数目比例进行确定。通过节理网络模型的中心点，分别设置水平、东西向竖直和南北向竖直截面，用以模拟不同方位的岩体露头(图 3)。在模拟露头上布置不同尺寸和形状的测窗，利用式(1)、式(2)和式(3)计算迹线中点密度，分析露头方位、测窗尺寸和形状的影响，评价不同计算公式的性能。

图 2 三维节理网络模型Fig. 2 3D discrete joint network model

图 3 不同方位的模拟露头示意图Fig. 3 Sketch of simulated outcrops with different orientations

2.2 计算结果及讨论

2.2.1 最大有效测窗

对于节理网络模型，由于“建模范围外的、有可能延伸到建模范围内的节理”的缺失，将使得边界处的迹线密度低于实际值。因此，计算迹线中点密度时，测窗不能过于接近模型边界。对于直径服从负指数分布的节理，其直径大于5倍均值的概率小于1%。因此，可以将5倍均值作为可能引起边界效应的直径阈值。换言之，在露头上距离边界大于2.5倍直径均值的范围内，可以认为节理迹线均匀分布，是计算迹线中点密度的有效范围。

根据表 2，优势组2的直径均值(2.64m)最大。因此，可以认为距离边界大于6.6m的露头内部区域为计算迹线中点密度的合理范围。因此，围绕露头中心布置86.8m×86.8m的方形测窗，即为计算迹线中点密度的最大有效测窗。最大有效测窗包含最多的有效数据，其密度计算结果最为可靠。

分别按照式(1)、式(2)和式(3)，计算最大有效测窗条件下的迹线中点密度如表 3所示。

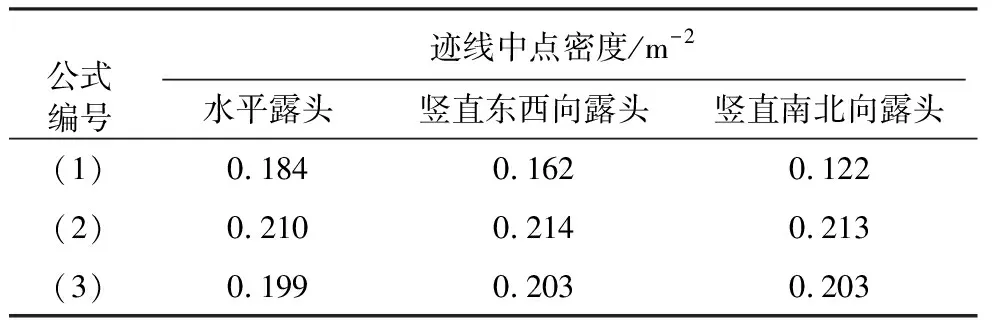
表 3 最大有效测窗条件下的迹线中点密度Table 3 Density of trace mid-point at the biggest effective survey window

对于同一个露头， 3个公式计算结果差异明显，这说明截长、尺寸和角度误差的影响显著。此外，对于不同的露头，式(2)和式(3)给出的迹线中点密度的相对变化率((3个露头中的最大值-3个露头中的最小值)/最小值)仅为2%，而式(1)的变化率可达50%。这说明角度误差使得来自同一节理网络模型的、方位不同的露头给出了差异显著的迹线中点密度。

2.2.2 测窗形状的影响

在图 3所示的每个模拟露头上，以中心点为圆心，分别以半径5m、6m、7m、…、43m布置圆形测窗，利用式(1)、式(2)和式(3)计算迹线中点密度。同时，对应于每个圆形测窗，按照等面积和中心点不变的原则，布置一个方形测窗，计算节理迹线中点密度。圆形与方形测窗的计算结果如图 4所示。对于式(1)，在水平、竖直东西向和竖直南北向露头上，由于测窗形状变化而引起的迹线中点密度变化率(两种测窗计算结果的差值与圆形测窗计算结果的比值)的最大值分别为6.3%、7.1%和14.3%； 对于式(2)，分别为6.6%、11.9%和16.4%； 对于式(3)，分别为6.1%、5.6%和11.5%。变化率最大值出现在较小测窗面积条件下。此外，两种测窗条件下，密度计算结果随着测窗面积的变化规律一致。因此，可以认为测窗形状变化不会引起迹线中点密度计算值的显著变化。

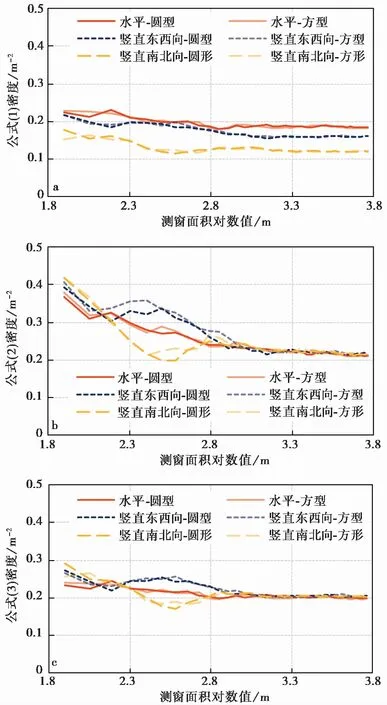
图 4 迹线中点密度计算结果Fig. 4 Results of trace midpoint density a. 仅修正截长和尺寸误差的计算结果； b. 仅修正角度误差的计算 结果； c. 联合修正截长、尺寸和角度误差的计算结果

2.2.3 测窗面积的影响

对于式(1)，当测窗面积对数值大于3时，随着测窗面积的增大，3个不同方位露头的迹线中点密度计算值趋于稳定(图 4a)。这说明，式(1)可以有效修正尺寸和截长误差。但是，3个不同方位露头的密度计算值并没有趋于一致(图 4a)。这说明，针对同一节理网络模型，式(1)给出了不同的迹线中点密度，即角度误差的影响显著。

对于式(2)，随着测窗面积的增大，3个不同方位露头的密度计算值趋于一致(图 4b)。这说明，式(2)可以消除角度误差。但是，3个不同方位露头的密度计算值并未趋于稳定，当测窗面积对数值大于3时，仍存在持续下降的趋势(图 4b)。这说明，式(2)未能消除截长和尺寸误差的影响。

对于式(3)，当测窗面积对数值大于3时， 3个露头上的密度与表 3中最大有效测窗条件下获得的计算值的差异均小于5%； 并且3个露头之间的密度相对变化率小于7%(图 4c)。即3个不同方位露头的密度计算值趋于稳定，并趋于一致。这说明，式(3)可以消除角度误差的影响，同时可以有效地控制截长和尺寸误差。

3 实例应用

北山坑探设施是我国高放废物处置地下实验室的先导工程(Wang et al.， 2018)，其硐口处的岩体露头平整清晰(图 5a)。利用综合测线法获得69条节理迹线的产状和迹长等信息(图 5b)。为计算节理迹线中点密度，在露头上按照以下两种方案布置测窗：方案1，沿露头最长测线方向、以0.5m为间隔连续布置半径为5m的圆形测窗(图 5b)； 方案2，以露头最长测线中点为圆心连续布置半径为5m、5.5m、…、10m的圆形测窗(图 5c)。

图 5 露头照片、节理迹线图及测窗布置方案 (实心点-测窗中心、圆形-测窗、直线段-节理迹线)Fig. 5 Outcrop photo， trace map and different designs of survey windows (solid point-center of survey window， circle-survey window， line-joint trace) a.山坑探设施开挖前硐口岩体露头照片； b. 测窗布置方案1； c. 测窗布置方案2

根据测窗布置方案1，计算获得的节理迹线中点密度结果如图 6所示。相比于式(1)和式(3)，式(2)给出的迹线中点密度的变化幅度更大，说明截长和尺寸误差随着测窗位置的变化而显著变化。式(3)的计算结果高于式(1)的计算结果(增大幅度在8.1%～14.5%范围内)，说明角度误差可以使得计算结果出现10%左右的偏差。当测窗位置变化时，尤其是测窗位于露头中部(即测窗中心到测线起点的距离为15～25m)时，式(1)和式(3)计算结果稳定，说明此区域内节理迹线的分布相对更为均匀； 根据式(3)结果，此区域内的迹线中点密度分布在0.117～0.147m-2范围内，均值为0.135m-2。

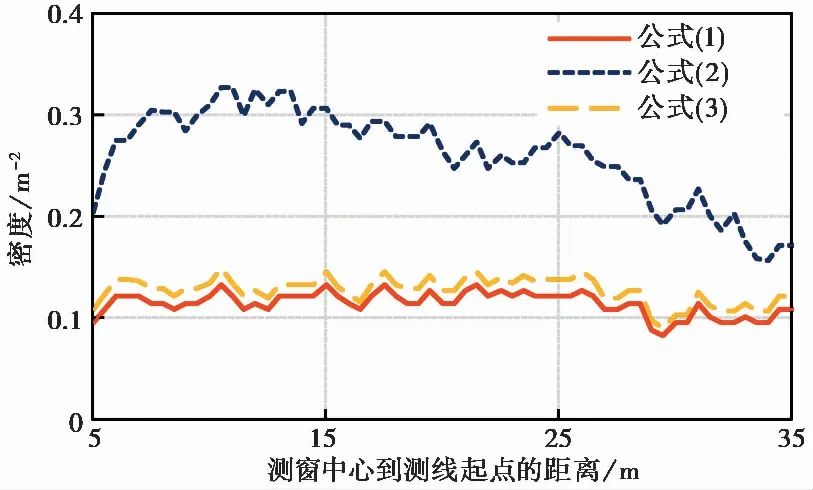
图 6 不同位置测窗上的节理迹线中点密度Fig. 6 Results of midpoint density of joint traces obtained from survey windows at different locations

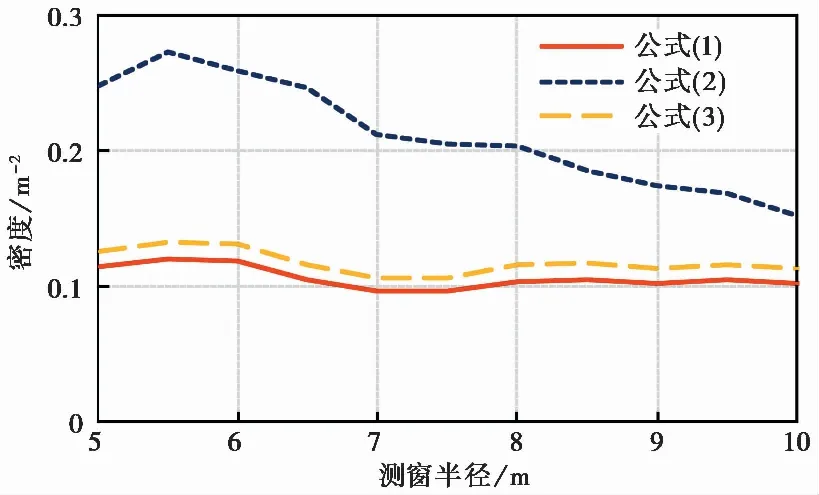
图 7 不同测窗半径条件下的节理迹线中点密度Fig. 7 Results of midpoint density of joint traces under different survey radii

根据测窗布置方案2，计算获得的节理迹线中点密度与测窗半径的对应关系如图 7所示。随着测窗半径的增大，式(2)计算结果整体上呈现逐渐减小的趋势，并逐渐接近式(3)计算结果； 而式(1)和式(3)计算结果更为稳定，并且式(3)的计算结果高于式(1)的计算结果。上述变化规律与2.2节所示的算例结果变化规律一致。因此，可以推断：岩体中节理分布特征与2.2节中的节理分布特征相似，即均满足“三维空间条件下节理中心点服从泊松分布”的假设。这说明，按照测窗布置方案2，分别利用式(1)、式(2)和式(3)计算节理迹线中点密度，可以为判定岩体中节理分布规律是否满足“三维空间条件下中心点服从泊松分布”假设提供佐证，继而为后续的节理三维分布特征分析和网络模型构建提供支撑。

上述分析结果说明，式(3)可以针对真实的岩体露头给出稳定可靠的节理迹线中点密度。同时，通过计算不同测窗面积条件下的迹线中点密度，可以测试和验证节理分布是否满足“三维空间条件下中心点服从泊松分布”假设，为后续的岩体统计均质区划分和三维节理网络建模等工作提供依据。

4 结 论

本文将角度误差修正系数引入到关联点密度计算方法中，提出了凸面测窗条件下同时修正截长、尺寸和角度误差的节理迹线中点密度计算方法。算例测试和实际应用结果表明：

(1)提出的新方法不需要进行节理优势组划分或节理迹长分布函数预估，对测窗方位和尺寸的变化不敏感。建议使用提出的新方法进行野外露头节理迹线中点密度计算。

(2)根据实例应用结果，建议分别利用截长和尺寸误差修正方法、角度误差修正方法以及提出的新方法，计算分析不同测窗面积条件下的迹线中点密度，为判定节理分布是否满足“三维空间条件下中心点服从泊松分布”的假设提供佐证。