快速路入口匝道控制策略综述
2021-09-18葛静张丽岩马健
葛静 张丽岩 马健

摘 要:随着城市规模的逐步扩大,机动车保有量和交通需求都有了明显增长,各种交通问题逐渐涌现出来。在众多问题中,日益严重的交通拥堵是各城市发展共同面临的社会问题,其中快速路的堵塞尤为严重。因此,如何通过实施合理的控制措施来缓解快速路交通拥堵,成为当前研究的重点,在众多的快速路交通控制策略中,匝道控制相关的研究较多,取得的效果也较好。本研究重点介绍了快速路入口匝道控制,根据对交通信息反应的区别可将入口匝道控制策略分为静态控制和动态感应控制;根据控制区域的范围将其分为单点控制和协调控制。最后在总结现有匝道控制策略的基础上,对未来的快速路匝道控制策略的研究方向进行了展望。
关键词:快速路;入口匝道;控制策略
中图分类号:F570 文献标识码:A
Abstract: With the gradual expansion of the scale of the city, the number of motor vehicles and traffic demand have increased significantly. All kinds of traffic problems emerge gradually. Among many problems, increasingly serious traffic congestion is a common social problem in the development of cities, especially the expressway congestion. Therefore, how to alleviate the traffic congestion of expressway by reasonable control measures has become the focus of the current research. Among the many expressway traffic control strategies, there are more researches on ramp control and better results. This study focuses on the on ramp control of expressway, which can be divided into static control and dynamic induction control according to the different responses to traffic information; according to the scope of control area, it can be divided into single point control and coordinated control. Finally, on the basis of summarizing the existing ramp control strategies, it looks forward to the future research direction of expressway ramp control strategies.
Key words: expressway; on ramp; control strategy
0 引 言
作為城市道路交通网络的骨干,快速路因其特点吸引交通流量日益增加,这极大地缓解了交通运输的压力,提高了城市的服务水平。然而由于缺乏合理的控制和有效的引导,快速路的安全和拥堵问题日益严峻,具体表现为高峰时期堵塞严重、车流运行速度缓慢、尾气排放加大等。这些问题导致快速路通行能力下降,安全风险增加,逐渐失去其优势,因此快速路交通主动控制是当前交通管理部门的研究重点。根据以往的经验,匝道控制是当前应用最为广泛可靠的方法,匝道控制的范围包括入口匝道和出口匝道,本研究将重点分析入口匝道的控制策略。
1 入口匝道控制策略分类
1.1 匝道关闭
匝道关闭就是通过采用人工护栏或放置交通禁行标志等方式,将部分入口匝道在某些特殊情况下进行暂时或永久性关闭。采用匝道关闭可有效解决因匝道问题带来的道路交通压力,增加快速路匝道合流区通行能力,缓解主线拥挤。但采用此方法大大增加了关联道路的交通流量以及车辆总行程时间,易引起出行者的异议,因此匝道关闭一般只在以下等特殊情况下采用:
(1)极端天气情况下易发生交通事故,此时可关闭入口匝道;
(2)当快速路发生事故等意外而造成路段瓶颈时,为防止交通状况进一步恶化可关闭入口匝道;
(3)当快速路系统已达饱和,再增加车辆易引起大面积堵塞,且附近有良好的绕道行驶路线时,可暂时关闭入口匝道。
1.2 入口匝道控制
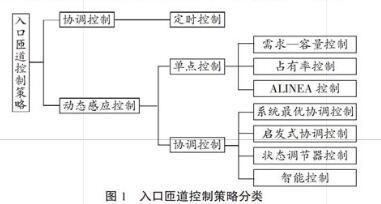
半个多世纪以来,国内外的学者始终致力于匝道控制算法的研究,提出了各种新的匝道控制策略,根据对交通信息反应的区别可分为静态控制和动态感应控制;根据控制区域的范围可分为单点控制和协调控制。匝道静态控制以
Wattleworth提出的定时控制为主,因此本文将入口匝道控制策略分为:定时控制、单点感应控制和协调感应控制,其分类具体情况如图1所示。
2 快速路入口匝道控制算法
2.1 定时控制
定时控制即假设某一时段的交通流运行状况以及控制周期和相位是近乎固定的,根据历史数据提前确定匝道控制率,常用方法是通过匝道信号灯进行匝道车辆的控制。该算法以匝道汇入主线的流量最大为目标,以快速路实际通行能力为约束,即匝道调节率r是由上游交通需求q、下游通行能力q和匝道期望汇入主线交通量q的关系来决定。当q≥q+q时,不会发生拥堵,因此不需要控制;当q
这种控制方法模型计算比较简单,但是只适用于交通流变化不大的路段以及10~30min的控制周期,一般可在交通流量有明显增加时使用。当交通流波动较大时,其控制效果十分有限,无法对实时交通变化和突发性拥挤做出相应处理,很难放到具体工程应用中。针对定时控制存在的不足,国内外学者从改进其目标函数或模型等多个角度对其进行了优化。Papageorgiou在充分考虑快速路入口匝道流量的变化以及其对下游影响的基础上,提出了快速路动态交通模型控制算法,可在较长的快速路实施控制,同时他还提出了分时段线性规划(Linear Programming , LP)控制方法。杨晓光则探究了快速路通行能力、车流运行速度以及出、入口匝道车流的排队约束,对传统LP控制算法进行优化,提出了动态LP控制算法[1]。
2.2 匝道单点控制
匝道单点控制的目的是改善该匝道的交通状况,常用方法有需求—容量控制(The Demand-Capacity Strategy)、占有率控制(The Occupancy Strategy)和ALINEA控制。
2.2.1 需求—容量控制
1975年,Masher提出了需求—容量控制[2],该方法中匝道调节率的确定也是通过比较q和q的关系得到的,目的是保证主线下游交通量在快速路通行能力范围内并最大化其利用率,算法具体描述如下:
rk= (1)
式中:rk为第k个控制时段的匝道调节率;r为最小调节率;qk-1为第k-1个控制时段主线上游交通量(veh/h);Ok-1为第k-1个控制时段主线下游占有率;O为临界占有率。
2.2.2 占有率控制
以需求—容量控制的研究为基础,Masher又提出了占有率控制,他利用检测器实时获取主线上游和下游的占有率,并通过经验公式估计下游流量来确定rk。当下游通行能力为负时,采取最小调节率,否则需通过公式估算,即:
rk= (2)
式中:v为自由流速度(km/h);g为调节参数,取决于检测器及车辆长度。
上述两种方法都属于开环控制,对外部干扰敏感度较高,但由于缺乏反馈机制,系统的稳定性相对较差。
2.2.3 ALINEA控制
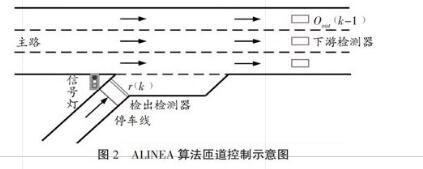
为了解决开环控制算法存在的问题,Papageorgiou等(1991)提出了一种局部交通反馈控制算法——ALINEA(Asservissement line'aire d'entre'e autoroutie're)[3]。与前两种控制方法不同的是,ALINEA是闭环反馈控制,它以经典自动控制理论作为算法基础,采用该算法时具体检测器布设示意图如图2所示,其具体控制过程为:在快速路匝道下游约40m处安装检测器以检测下游实时占有率,通过比较实时占有率与预先设定的下游期望占有率来确定匝道调节率,匝道车流的汇入通过信号灯控制,从而保证主线下游的车辆运行处于理想状态。同时该方法还考虑了上一控制周期的调节率,可以避免本周期的匝道调节率出现较大的波动,保证车流的平稳运行。
ALINEA算法的基本模型为:
rk=rk-1+K-Ok-1 (3)
式中:K調节参数;为主线下游期望占有率。
上式在经典自动控制理论中被称为I型(积分)调节器,可以看出当交通流在相邻时段变化不大时,如匝道上游交通量q为常数或变化很小,此时该调节器会自动调整使下游占有率O=,这一特性可有效避免匝道上游交通量的任何变化以及其他有可能的干扰。一般取值等于或接近O,而O需通过下游流量—占有率q—o基本原理图来设立,如图3所示。ALINEA控制策略自被提出后,已在欧洲多个地区通过实地检验证明了其控制效果的可靠性,尤其是在提高车流平均速度、降低路网行程时间以及稳定交通流方面。需求—容量控制和占有率控制是在临界状态时才对匝道进行控制,而ALINEA对于-Ok的细微差别处理更加顺畅,可以最大限度保证下游的运行容量,使交通流更加稳定,避免堵塞。
ALINEA在实际应用中还存在一些缺陷,如:经典ALINEA控制没有考虑匝道排队溢出问题,易使入口匝道及关联交叉口出现排队过长的现象;控制范围仅为单个匝道,缺乏对多匝道协调控制的探讨,难以实现系统最优。因此不少学者对其基本模型进行了优化,Zhang等对基本ALINEA模型进行了扩展,可避免匝道交通量超过其通行能力[4]。Papageorgiou和Smaragdis提出了FL-ALINEA、UP-ALINEA和X-ALINEA/Q等扩展算法[5],可提高模型在各种场景下的性能。FL-ALINEA采用来自匝道下游检测器的主线流量数据,当下游检测器失效时,UP-ALINEA使用来自上游检测器的占用率值。X-ALINEA/Q则通过限制匝道调节率,针对性解决了快速路达到最大通行能力时匝道排队的问题。Papageorgiou提出的PI-ALINEA算法可有效缓解匝道下游的交通瓶颈[6],Smaragdis等引入自适应控制,通过估计器获取匝道下游实时期望占有率,提出了AD-ALINEA,该方法解决了由于天气或交通组成而可能改变恒定期望占有率值的问题,适用于交通流状态变化较大、临界占有率不稳定的路段。郑飞等探索了ALINEA算法的参数设定,通过对实际道路展开匝道动态控制并分析采集的数据,构建了匝道排队分段约束模型,并设立控制阈值表,仿真表明该方法可平滑匝道流量脉冲,提高匝道下游车流平均速度,缓解交通拥挤[7]。
2.3 匝道协调控制
匝道单点控制仅仅提高了单个匝道层面的运行效率,难以实现系统最优,而匝道协调控制考虑上下游若干匝道的调节,充分利用每个匝道的空间容量,改善快速路系统。这样不仅可减轻某一处匝道的排队压力,还能缓解主线交通拥堵,从而弥补匝道单点控制的不足,达到系统最优。常用的匝道协调控制方法包括以下四种:
2.3.1 系统最优协调控制(Systematic optimal control)
早在1965年,Wattleworth和Berry教授就已展开将匝道控制问题转化为一个线性规划问题的研究。系统最优协调控制一般以路网行程时间最小、通行流量最大等为目标函数,主线、匝道通行能力及主线限速等为约束条件,根据实时检测的交通流状态信息,求解交通流控制模型得到路网最优的交通状态和匝道调节率。该方法有明确的控制模型及目标函数,理论上可以实现系统最优,但其算法求解困难,可能会出现无最优解的问题,且对交通状态预测的要求高,因此当交通需求预测的准确度较低时,难以达到预期控制效果。同时该方法对交通异常状态的反应很差,缺少反馈机制;一般默认通过设立约束条件使主线保持良好运行状态,很难建立主线在拥堵或事故状态下的交通模型。目前对于系统最优协调控制的大部分研究还处于理论探索阶段,在实际应用中控制效果一般,但随着智能技术的不断进步,其研究前景依然非常广阔。
2.3.2 启发式协调控制(Heuristic control)
启发式协调控制不需要具体的目标函数,也不需要求实时最优解,具有一定的反馈机制,可操作性高。该方法包括合作(Cooperative)控制和競争(Competitive)控制,合作控制中具有代表性的算法有Linked-ramp、Helper算法等,Helper算法由Lipp等提出,于1981年首次部署在科罗拉多州丹佛地区的某高速公路上,该方法将高速公路分为六组,每组包括1~7个入口匝道,并定义了六个可选匝道调节率,当某个入口匝道出现排队时,系统将通过协调控制将该匝道的交通量有序分配至上游匝道,直至拥堵缓解结束协调控制。
竞争控制主要包括Bottleneck算法和Swarm算法等,Bottleneck算法最早是由华盛顿州交通部Jacobson等开发,首先确定每个匝道的调节率,然后当主线出现瓶颈即该处占有率超过阈值时,激活控制算法,协调控制区域内所有关联匝道的调节率,将计算的调节率减少总量按比例分配至每个匝道,最后比较每个匝道的两个调节率,取其中较小者作为其调节率,该方法实时性好,执行效率高,对匝道单点控制策略的鲁棒性要求高。Swarm算法由Paesani等提出,该算法可分为两层:协调控制(SWARM1)和局部控制(SWARM2),SWARM1是利用检测器检测实时的交通数据,然后通过线性回归及卡尔曼滤波进行交通流预测,根据期望密度计算上游控制区域内每个匝道的调节率[8],SWARM2中匝道调节率是根据快速路和匝道检测到的交通流车头时距来计算的,该算法已被应用于洛杉矶的多个洲际高速公路,控制效果较好。
2.3.3 状态调节器控制(State regulator control)
状态调节器控制中最典型的算法是METALINE,属于ALINEA的一个扩展算法[9],其基本模型为:
rk=rk-1-Kok-ok-1-KOk- (4)
式中:ok为第k个控制时段主线重要路段占有率;Ok为第k个控制时段主线下游占有率;K、K为反馈增益矩阵。
METALINE与ALINEA算法相似,其控制思路和算法求解比较简单,并且比ALINEA更具系统性,对交通流状态的变化更为敏感,在实际中获得了广泛应用。但其缺点也很明显,如多匝道算法标定比较复杂;城市快速路入口匝道密度较大,在经常性拥堵的情况下,该算法就失去了优势;当快速路交通状态发生强烈变化如因事故等引起严重拥堵时,系统难以达到理想状态,此时的控制效果很差。
2.3.4 智能控制方法(Intelligent control)
由于传统控制方法难以应对日益复杂的交通系统,因此许多学者开始利用智能控制算法,常用的有模糊控制、遗传算法以及神经网络等。Pappis等在进行单个交叉口控制时最先采用了模糊控制,并通过仿真证明该方法可有效降低系统车流的平均延误。20世纪80年代,Chen提出利用模糊控制对单入口匝道进行控制,随后Taylor等通过实验证明该方法可有效预防高速公路交通拥挤,并且比传统的匝道控制效果更好。陈德望结合了模糊控制和神经网络,通过仿真证明了该智能控制方法适用于任何交通模式,并可在有效保持主线交通流处于理想密度的同时,尽可能减少入口匝道排队[10]。乔良等采用深度Q网络构建强化学习模型来解决无人驾驶汽车匝道汇入问题,主要从车间通信和单车控制的角度讨论了单点匝道的汇入控制,缺乏对匝道区域内车辆的协调和对交通流的引导[11]。罗孝羚则是提出了一种网联环境下的匝道车流汇入轨迹优化算法,通过仿真实验证明所提出的模型可以使车辆总延误减少59.7%,实现车辆以较高的速度通过匝道交通区域[12]。目前智能环境下的匝道控制研究重点在于匝道车辆的汇入控制微观研究,缺少对快速路匝道区域内车辆的协调控制,且由于当前主流的交通仿真软件难以实现智能环境下控制框架的构建,一般需通过二次开发实现个性化研究需求,增加了研究者的研究成本。
3 结束语与展望
本文围绕快速路入口匝道这一场景,介绍了目前常用的入口匝道控制算法,定时控制是最简单的控制策略,在交通流变化较小时十分有效,但难以处理交通流状况发生突变的情况。匝道单点控制提高了单个匝道的运行效率,但是该方法并未考虑交通流干扰,可能会影响相邻匝道的通行效率,因而无法达到系统最优。匝道协调控制是在单点控制的基础上,协调控制上下游若干个匝道,实现整个快速路主线的畅通。随着车路协同和智能网联技术的兴起与发展,当前的研究热点是将各种智能控制算法与匝道控制相结合,可有效提高匝道控制的效果和可靠性,未来可在这些方面作进一步研究。
参考文献:
[1] 杨晓光. 考虑进出口匝道排队约束的城市快速道路交通系统动态控制方法[J]. 长安大学学报(自然科学版),1999(2):20-26.
[2] Masher D P, Ross D W, Wong P J, et al. GUIDELINES FOR DESIGN AND OPERATION OF RAMP CONTROL SYSTEMS[R]. Stanford Research Institute, 1975.
[3] Papageorgiou M, Hadj-Salem H, Blosseville J M. ALINEA: A local feedback control law for on-ramp metering[J]. Transportation Research Record Journal of the Transportation Research Board, 1991,1320:58-64.
[4] Zhang M, Nie X, Jin W, et al. Evaluation of On-ramp Control Algorithms[D]. California: University of California, 2001.
[5] Smaragdis E, Papageorgiou M, Kosmatopoulos E. A flow-maximizing adaptive local ramp metering strategy[J]. Transportation Research Part B Methodological, 2004,38(3):251-270.
[6] Wang Y, Papageorgiou M, Gaffney J, et al. Local ramp metering in the presence of random-location bottlenecks downstream of a metered on-ramp[C] // International IEEE Conference on Intelligent Transportation Systems, 2010.
[7] 鄭飞,杜豫川,孙立军. 基于ALINEA算法快速路入口匝道单点动态控制[J]. 同济大学学报(自然科学版),2009,37(6):766
-771.
[8] 陆海亭,张宁,钱振东. 高速道路入口匝道控制方法及应用探索[J]. 公路,2008(8):180-186.
[9] 康平允,干宏程,袁鹏程. 快速路入口匝道控制方法探究[J]. 物流工程与管理,2016,38(3):201-203.
[10] 陈德望,王飞跃,陈龙. 基于模糊神经网络的城市高速公路入口匝道控制算法[J]. 交通运输工程学报,2003,3(2):100-105.
[11] 乔良,鲍泓,玄祖兴,等. 基于强化学习的无人驾驶匝道汇入模型[J]. 计算机工程,2018,44(7):20-24,31.
[12] 罗孝羚,蒋阳升. 智能网联车环境下高速匝道汇入车流轨迹优化模型[J]. 交通运输系统工程与信息,2019,19(4):94-100.
