曲柄摇杆机构预定轨迹的优化设计与仿真
2021-09-18孙道宾李元皓
孙道宾,李元皓
(沈阳理工大学 机械工程学院,辽宁 沈阳 110159)
曲柄摇杆机构是一种较为常见的传动机构,在多个领域都有广泛的应用,许多研究者曾致力于其结构的优化设计。俄罗斯数学家切贝雪夫为此建立了解析法。这种解析法综合运用逼近论、数学矩阵、复数等知识,能对二次线性方程或者超越方程进行求解,但求解过程相当麻烦。解析法最多只能按照9个点进行求解设计,求解精度有待提高,且最后得到的只有一组可行解。美国的F·Ferudesnetin通过设置精确点,首次使用计算机实现了四杆机构再现函数的最优综合。从此,人们开始了采用计算机对连杆机构进行综合分析设计的进程。R·L·Fox和K·D·Willmert于1967年,J·Tomas于1968年,先后把优化方法与计算机技术结合起来,进行机构设计(称作机构最优化设计),从而开始了机构优化设计的新进程,推动了优化设计方法的应用[1]。
本文针对机器人足端轨迹,在椭圆轨迹的基础上重新规划,以期获得具有更强稳定性的机器人足端新规划轨迹,并通过Matlab编程实现新规划轨迹的曲柄摇杆机构设计,进而设计机器人的单条腿部机构。
1 机器人足端轨迹的确定
曲柄摇杆机构经常被用作机器人的行走机构。本文将曲柄摇杆机构作为机器人的腿部机构。机器人足端轨迹如图1所示。采用这种椭圆轨迹的优点是能够保证机器人足端与地面接触时的速度和加速度都为零,从一定程度上减轻机器人足端与地面碰撞的强度,提高机器人腿部机构的使用寿命。若地面为非理想状态,机器人足端在着地瞬间的速度和加速度都为零,只能向上抬腿,则机体的倾斜或者摆动腿落地位置的地面下陷,都会导致在机器人的摆动腿还未落地时其着地腿就已经抬了起来,使机体的稳定性大为降低。换句话说,这种机器人足端轨迹(图1(a))根本无法满足机器人实际行走稳定性的要求,因此需要在椭圆轨迹的基础上重新规划机器人足端轨迹。
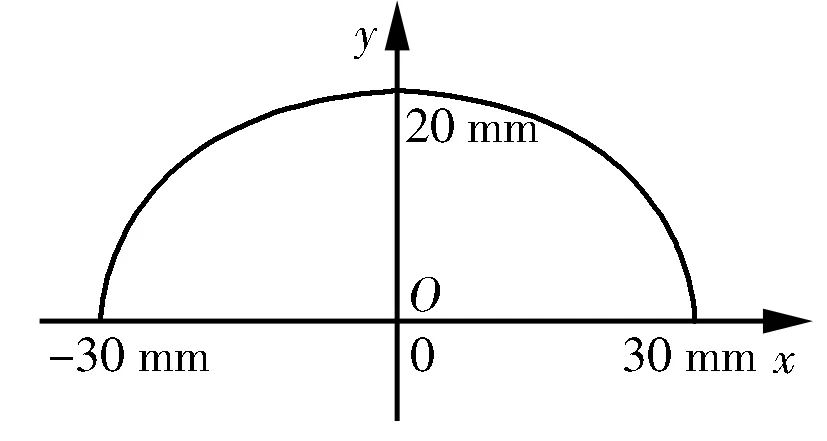
(a) 椭圆轨迹

(b) 新规划轨迹图1 机器人足端轨迹

1.1 建立足端轨迹方程
根据图1中新规划轨迹可建立对应的机器人足端轨迹方程。
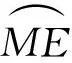
(1)

(2)

(3)
对应直线MN的轨迹方程为:
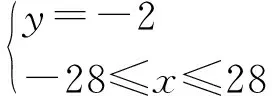
(4)
1.2 确定足端轨迹上若干点的坐标
本文首先在机器人足端轨迹上取12个点,然后根据足端轨迹方程,计算这12个点的坐标值(表1)。

表1 足端轨迹上12个点的坐标值
2 曲柄摇杆机构的运动分析
基于坐标系Oxy,可对曲柄摇杆机构(图2)进行运动分析。

图2 曲柄摇杆机构
本文参考相关文献[2-4],针对曲柄摇杆机构OAABOB,设OAOB=L0、OAA=L1、AB=L2、BOB=L3、APj=L4,且令APj与AB为固联。通过矢量分析,有:
(5)
由式(5)消去θj可得:
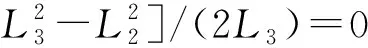
(6)
令
E1j=L0cosα-L1cosφj,
E2j=L0sinα-L1sinφj,
E3j=[(L0cosα-L1cosφj)2+(L0sinα-
则
E1jcosΨj+E2jsinΨj+E3j=0
(7)
根据三角函数知识可列出:
cosΨj=[1-tan2(Ψj/2)]/[1+tan2(Ψj/2)]
(8)
sinΨj=2tan(Ψj/2)/[1+tan2(Ψj/2)]
(9)
把式(8)和式(9)代入式(7)中,得到关于tan(Ψj/2)的一元二次方程式后求解,可得:
(10)
将式(10)代入式(5),可得:
θj=tan-1[(E2j+L3sinΨj)/(E1j+L3cosΨj)]
(11)
设OA点的坐标为(OA,x,OA,y), 实际轨迹上Pj点的坐标为(Pj,x,Pj,y);则
(12)
为了让曲柄摇杆机构运动时灵活轻便、传动时节省动力,设计时应使其最小传动角γ大于等于其许用传动角[γ]。由机械原理可知,曲柄摇杆机构的最小传动角γ和杆AB杆BOB的夹角δ有关,当δ≤90°时,γ=δ;当δ>90°时,γ=180°-δ。由此推算出:
[γ] ≤δ≤ 180° - [γ]
(13)
令δmin= [γ],δmax=180° - [γ];则
δmin≤δ≤δmax
(14)
即
cosδmin≥ cosδ≥ cosδmax
(15)
在机构运转过程中δ是不断变化的,当曲柄OAA与机架OAOB重合共线时,δ为最小值。此时有:
(16)
当曲柄OAA与机架OAOB拉直共线时,δ为最大值。此时有:
(17)
通过运动分析可知,曲柄摇杆机构的设计应满足式(15)成立的条件。
3 数学模型的建立
3.1 建立目标函数
为了尽可能地让曲柄摇杆机构上点的实际轨迹与预定轨迹重合,可根据机构实际轨迹上的点坐标与预定轨迹上的点坐标差值的最小平方和来建立下列目标函数[5]:
(18)
式中:(Pj,xPj,y)为机构实际轨迹上一系列点的坐标;(P′j,xP′j,y)为预定轨迹上一系列点的坐标。
假设曲柄OAA起始位置与机架OAOB之间的夹角为φ1, 若给定一系列预定轨迹点P′的坐标(P′j,x,P′j,y)以及对应的曲柄OAA转角(相对于曲柄OAA起始位置的夹角)φj,1, 则图2中的φj可表示为:
φj=α+φ1+φj,1;j= 1,2,…,n
(19)
综合式(12)和(19),可得:
(20)
3.2 设定设计变量
分析可知,在已知一些有规律的预定轨迹上点P′的坐标(P′j,x,P′j,y)以及对应的曲柄OAA转角φj,1时,目标函数F(X)与参数L0、L1、L2、L3、L4、α、β、φ1、OA,x、OA,y都有一定的关系。这些参数就是设计变量。为了让设计变得简单,可以在设计前预先给定OA,x、OA,y的值[6-7]。
取(OA,x,OA,y)=(-75,-0),则设计变量可设定为:
X=[x1,x2,x3,x4,x5,x6,x7,x8]T= [L0,L1,L2,L3,L4,α,β,φ1]T
(21)
3.3 设定约束条件
本文所研究曲柄摇杆机构在满足曲柄存在的条件下,为了让其运动顺畅灵活、节省动力,还应该满足传动角的约束条件。
曲柄存在必须满足下列条件:
(22)
根据式(22)可写出曲柄存在的约束条件,即
(23)
根据文献[8],结合式(15),可写出传动角的约束条件,即
(24)
通常,许用传动角[γ] = 40°,故δmin=[γ]=40°,而δmax= 180° - [γ] = 140°。
根据cos 40°=0.766 0,以及式(16)、式(17)、式(24)推导,可得:
(25)
进一步推导可知,传动角的约束条件为:
(26)
综合式(23)和式(26)可知,目标函数F(x)的约束条件为:
(27)
3.4 求解目标函数
对于多约束非线性优化问题,可采用Matlab自身库中fmincon函数来求解[9]。非线性约束优化函数的数学模型为:
[X*,fval]=fmincon(@objectf1,x0,A,b,Aeq,beq,lb,ub,@conf1,options)
(28)
式中:X*为设计变量的优化解;fval是对应于该解的函数值;@objectf1为调用函数的文件名;x0为初始点, 其取值必须满足约束条件,本文取x0=[120,35,110,45,70,-30,10,30];A为线性不等式约束条件下的系数矩阵,且A(1,:)=[1,1,-1,-1,0,0,0,0],A(2,:)=[-1,1,1,-1,0,0,0,0],A(3,:)=[-1,1,-1,1,0,0,0,0],A(4,:)=[0,-1,0,0,0,0,0,0];b为线性不等式的常数向量,b=[0;0;0];因本文的x0、A、b中不存在线性等式约束,所以Aeq和beq皆为空阵;lb为设计变量的下界,本文中lb=[0,0,0,0,0,-180,0,0];ub为设计变量的上界,本文中ub=[],即空阵;@conf1为根据非线性约束条件所写约束程序的函数名。本文中只有传动角约束为非线性约束,可针对它编写相关的约束函数[10]。其程序格式为:
function[c,ceq]=conf1(x);
c(1)=cos δmin-cos(40pi/180);
c(2)=cos(140pi/180)-cos δmax;
ceq=[]。
这里ceq为空阵,表示不存在非线性等式约束。 限于篇幅,本文的主程序和目标函数程序不在此列出。
经过Matlab程序运算,得到的设计变量优化解为:
X*=[x1,x2,x3,x4,x5,x6,x7,x8]T=
[L0,L1,L2,L3,L4,α,β,φ1]T=
[120.632 8,30.993 1,114.681 4,44.649 5,
74.788 3,-20.319 6,5.809 2,26.602 3]T;
目标函数的优化值为:F(X*)= 3.229 5。
可见, 其实际轨迹点与预定轨迹点的点距误差已相当小。实际使用时,还可通过改变收敛精度系数进一步缩小点距误差,使所设计机构更好地满足使用要求。
4 机器人足端轨迹的仿真验证
通过仿真可知,对应于优化设计的曲柄摇杆机构,机器人足端实际轨迹与新规划轨迹已经非常接近。利用UG NX软件建立曲柄摇杆机构的三维模型,依据Matlab软件求解的数据,可进行曲柄摇杆机构的轨迹追踪,进而比较实际轨迹与新规划轨迹。
按机器人足端预定轨迹仿真优化后设计的机器人单条腿部机构如图3所示。仿真所得机器人足端轨迹如图4所示。
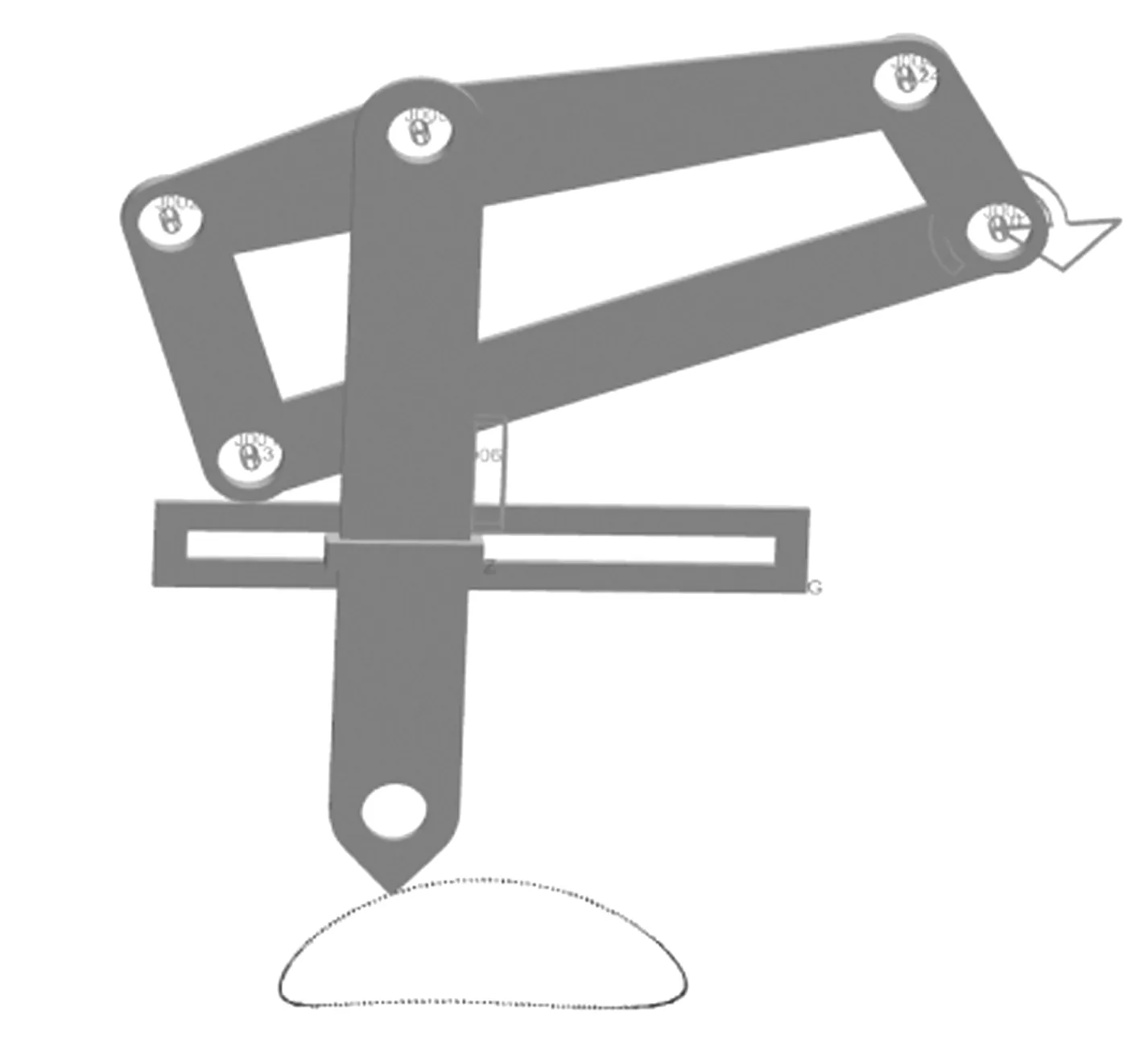
图3 机器人的单条腿部机构
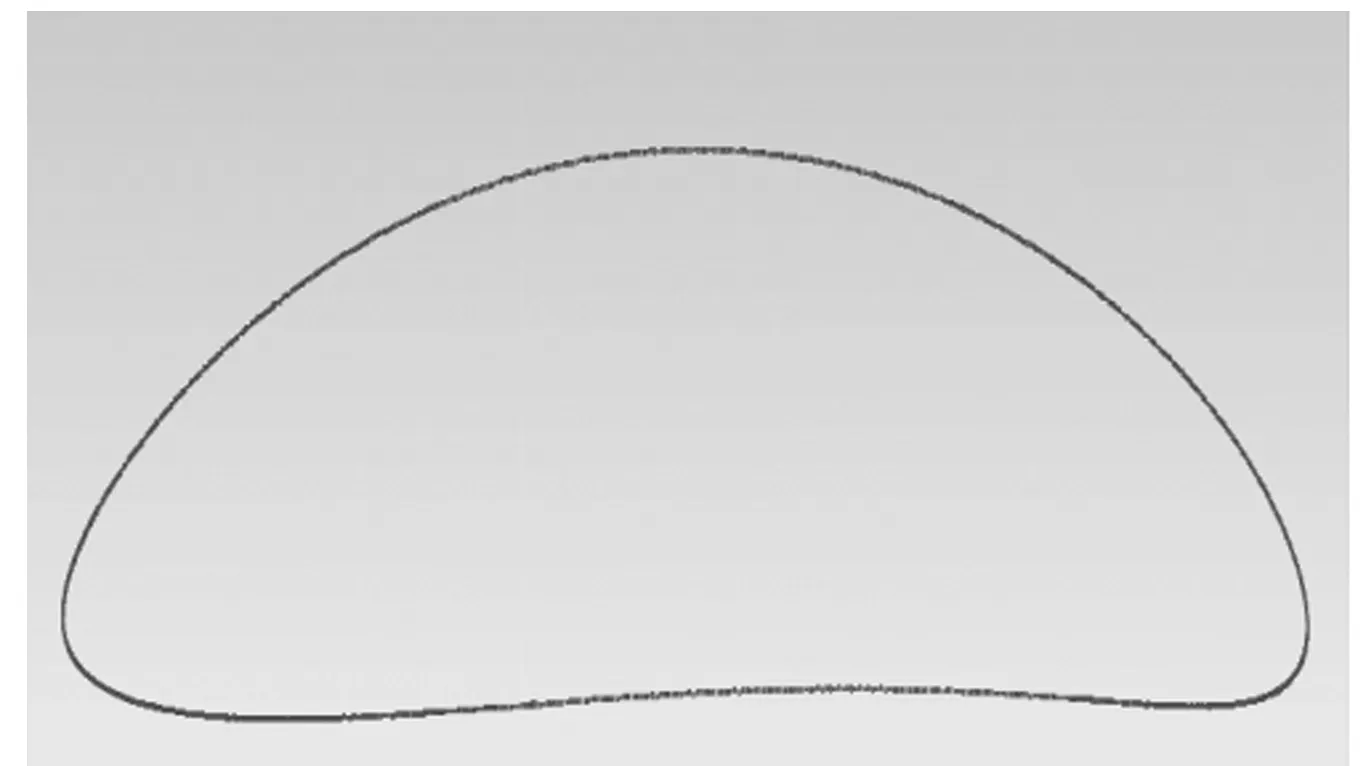
图4 仿真所得机器人足端轨迹
对比图1和图4可知,机器人足端仿真轨迹与新规划轨迹基本一致。
5 结束语
本文以曲柄摇杆机构为例,通过建立数学模型,进行多约束条件下预定轨迹的优化设计;基于Matlab平台对椭圆轨迹进行再规划,在一定程度上可以解决机器人足端椭圆轨迹在非理想地面稳定性不足的问题。利用Matlab自身库中fmincon函数对多约束条件下曲柄摇杆机构的优化求解,实现了设计过程的简化。通过UG NX动力学模型验证可知,新规划轨迹与仿真轨迹大致相同,机构设计效果理想,所用设计方法能大大提高连杆机构设计的效率和质量。
