爆破冲击荷载作用下连续刚构桥动力响应分析
2021-09-18李云虎尹万杰邹辉煌潘怡宏
李云虎,尹万杰,邹辉煌,潘怡宏
(中国市政工程中南设计研究总院有限公司,湖北 武汉 430010)
0 引言
桥梁作为国家重要交通基础设施的组成部分之一,发挥着改善交通系统,促进经济发展等重要作用。由于桥梁在使用过程中,不可避免地会发生爆炸,对桥梁结构产生损害,甚至产生不可修复的破坏,导致交通系统停滞和相关人员伤亡。所以研究爆破荷载作用下,桥梁的动力响应以及相关损伤评估,对桥梁修复以及破坏后使用功能评价具有重要意义[1,2]。
本文采用ANSYS 有限元软件建立连续梁桥有限元模型,在不同当量和爆破距离条件下,进行爆破荷载作用下,桥梁动力响应分析以及损伤分析,对比不同桥梁断面承受爆破荷载能力。
1 有限元概况
本文分析采用的桥梁模型为某连续T 型刚构梁桥,见图1。该桥桥跨布置为140 m+268 m+140 m,桥面宽16 m,箱梁为变截面预应力混凝土箱梁。主梁和桥墩均采用C60 混凝土。

图1 某连续T 型刚构梁桥(单位:mm)
在把握结构的主要受力特征的基础上,建立由不同单元类型组成的ANSYS 有限元模型。本文采用梁单元与实体单元连接:爆破荷载作用部分分析的梁截面采用实体单元solid65,其余梁截面采用梁单元beam4,不同单元连接处采用刚性梁法进行连接,保证受力整体性。预应力混凝土梁结构进行实体建模时,采用分离式有限元模型建模,即混凝土单元采用solid65 实体单元,预应力筋采用Link8 单元,预应力与混凝土之间采用共用节点模拟混凝土与预应力之间的连接作用,采用降温法施加预应力。主梁中的普通钢筋不予考虑,当爆炸荷载作用与桥墩时,实体桥墩结构中的钢筋采用配筋率模拟钢筋混凝土桥墩。
2 爆炸荷载模拟
爆炸荷载实质为一种冲击荷载,作用时间极短,一般为毫秒级,瞬间产生的超压峰值极大,实际中的爆炸空气冲击波荷载非常复杂,基于目前数值模拟的局限性,在保证计算精度的要求下,对爆炸荷载进行简化。
在实际爆破结构分析设计中,为了简化计算,常将空气冲击波压力衰减曲线简化为线性下降三角形冲击波压力衰减曲线[3-5],等效冲击波公式可以表示为:

式中:ΔP+为等效冲击波侧向超压幅值;Ta为等效冲击波作用时间。

实例分析中,考虑到汽车炸弹或者易燃易爆品爆炸的因素,现假设在桥上爆炸TNT 当量分别为100 kg、150 kg、200 kg,爆炸中心O 距离桥面2.5 m高,作用范围为2.5~3 m,采用不同距离范围内压力平均值在相应范围内代替,作用范围为5.5 m×5.5 m。
通过分析可以得到本实例分析的桥梁爆炸压力时程荷载曲线,以,爆破荷载时间曲线见图2。

图2 实例中桥面三角爆炸压力时程曲线
3 有限元模型建立
根据爆炸荷载作用位置不同,分别为跨中,1/4跨两种荷载作用位置,分为两种有限元模型,不同荷载作用位置见图3。全桥有限元模型单位采用国际制单位,以下云图中挠度的单位为m,应力为单位为Pa,其中混凝土图应力压为负值,拉为正值。

图3 控制截面示意图(单位:mm)
控制截面选取跨中截面时,有限元模型见图4(a),实体单元长度为16 m,共有65 018 个单元。自重作用下,实体单元应力云图见图4(b),挠度云图见图4(c)。

图4 有限元模型概况以及自重荷载作用下实体单元云图(荷载作用于跨中)
控制截面选取1/4 跨截面时,有限元模型见图5(a)所示,实体单元长度为25m,共有84 165 个单元。自重作用下,实体单元应力云图见图5(b),挠度云图见图5(c)。

图5 有限元模型概况以及自重荷载作用下实体单元云图(荷载作用于1/4 跨)
4 损伤特性分析
4.1 损伤工况
将TNT=250 kg 荷载曲线加载在中跨跨中中心区域内,进行ANASYS 瞬态分析后得出结构的挠度和应力分布见图6、图7。

图6 自重和爆炸作用下应力云图(单位:P a)
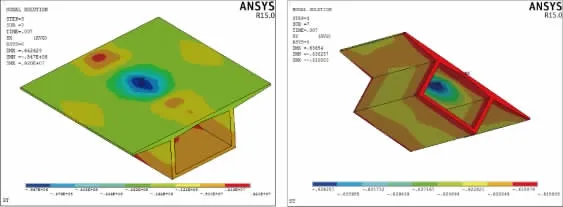
图7 自重和爆炸作用下挠度云图(单位:m)
爆炸冲击荷载作用时间极短,本文中荷载作用时间最长只有0.006 s,但是为了能够更加清楚地了解爆炸荷载作用时间内模型截面内力及变形变化,荷载作用范围内选取典型节点,将挠度以及应力时间变化曲线绘制见图8, 这里需要说明一下,从0~0.001 s 只有自重作用,0.001~0.007 s 为自重作用+ 爆炸荷载作用。

图8 挠度以及应力时间变化曲线
从图8 中可以看出,在爆炸荷载作用下,挠度随着时间的增加而增大,应力变化随着时间的增大然后减小,在最后0.002 s 内,荷载作用位置应力出现缓慢恢复。所以,爆炸荷载作用完毕之后,模型应力并不最大。为了更加清晰地表现模型在不同时刻应力变化,分别将爆炸荷载时间0 s,0.002 s,0.004 s 和0.006 s 模型应力云图绘制于图9。

图9 跨中1/2L 处应力图(单位:P a)
分别采用不同TNT 当量,提取结构关键点截面的应力数据如下,与仅在自重作用下的应力对比:找出不同TNT 当量值临界爆距,即某当量值对应该爆距时,截面应力刚好达到混凝土极限应力(此应力考虑冲击荷载作用下混凝土极限强度提高系数),将变化曲线绘制于图10,其中安全区与危险区是指,受爆破荷载作用,桥面只要发生拉应力大于混凝土极限拉应力就视为破坏。

图10 不同爆破荷载作用下主梁断面破坏情况
4.2 不同工况对比
为了对比1/2 跨和1/4 跨主梁断面抵抗爆破荷载作用的能力,以1/2 跨主梁断面混凝土达到拉应力极限强度的爆破荷载作用参数为临界值,作用于1/4跨,对比两种不同断面在相同荷载作用下的响应变化,结果列于表1 中。总体来看,相同爆破荷载作用下,1/4 跨最大拉应力要大于1/2 跨中,而1/4 跨最大压应力要小于1/2 跨。说明桥梁主梁断面梁高不同,相同荷载作用在与不同梁截面,荷载作用响应不同;1/2 跨中梁高较小,爆破荷载作用后,桥梁截面顶板和底板都出现破坏,而对于1/4 跨梁截面高度较高,相同荷载作用后,仅有桥梁顶板出现较大的拉裂破坏。
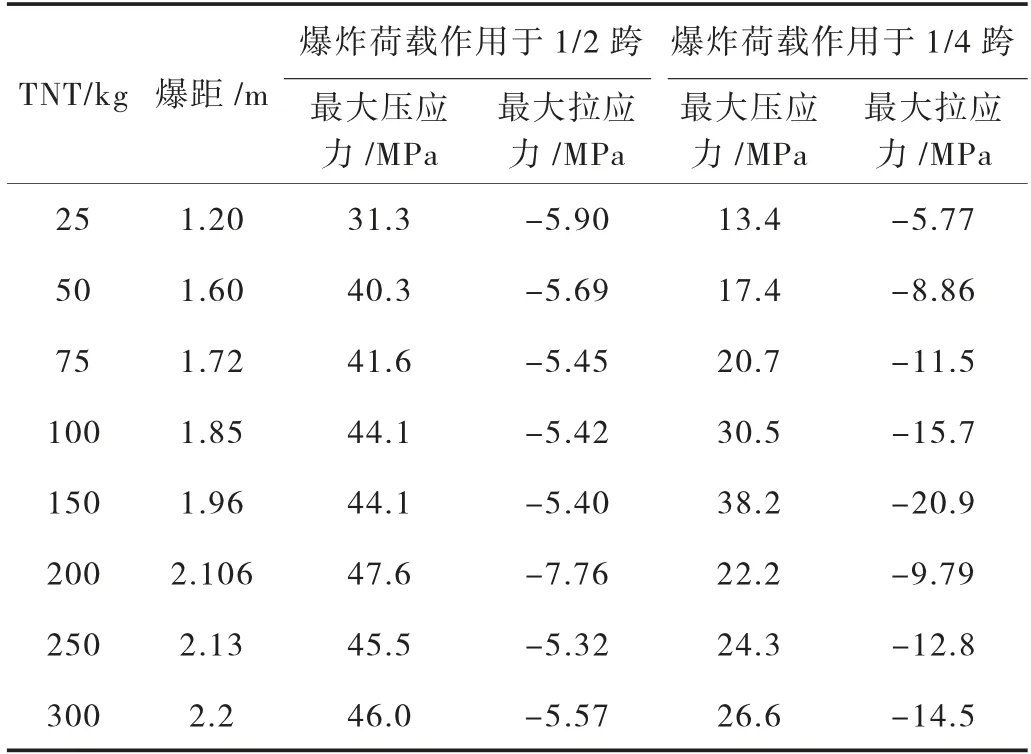
表1 爆炸荷载作用于1/2 跨与1/4 跨主梁断面应力响应
5 结论
本文采用ANSYS 有限元软件建立连续梁桥有限元模型,在不同当量和爆破距离条件下,进行爆破荷载作用下,桥梁动力响应分析以及损伤分析,结论如下:
(1)在爆炸荷载作用下,挠度随着时间的增加而增大,应力变化随着时间的增大然后减小,最后应力值有所恢复;
(2)相同爆破荷载作用在与不同梁截面,荷载作用响应不同;1/2 跨中梁高较小,爆破荷载作用后,桥梁截面顶板和底板都出现破坏,而对于1/4 跨梁截面高度较高,相同荷载作用后,仅有桥梁顶板出现较大的拉裂破坏;
(3)爆破荷载作用下,桥梁的损伤程度与当量值以及爆破距离有关。
