地下水渗流作用下的三峡库区巴东县赵树岭滑坡稳定性研究
2021-09-18刘秋强胡嫚吕杰堂程凯
刘秋强,胡嫚,吕杰堂,程凯
(1.有色金属矿产地质调查中心,北京 100012;2.西南大学工程技术学院,重庆 400715;3.自然资源部地质灾害技术指导中心,北京 100086 )
0 前言
中国是世界上滑坡分布最广、危害最严重的国家之一。滑坡灾害数量近百万之多,平均每年造成数百人死亡,数十亿元的经济损失。地下水渗流作用是诱发滑坡灾害的因素之一。大量的事故表明,土质边坡的失稳在滑坡事故中占有很大的比例,而地下水渗流则是诱发边坡失稳的关键因素,对坡体的稳定系数起着决定性的作用。据统计,约90%的自然边坡和人工边坡的破坏与地下水作用有关。地下水渗流诱发边坡失稳主要由于土体的含水率增加,发生非稳定渗流,增加土体的重量和滑动力(谢罗峰,2009)。在工程实例中,不乏有许多学者通过对滑坡稳定性分析研究分析为滑坡治理决策提供理论支撑,从而减少事故损失(张秦华等,2019;张啟兴等,2019)。所以,正确认识滑坡中的地下水分布情况及其对滑坡稳定性的影响规律,能够有效指导滑坡防治,减少事故损失。
一直以来,众多学者对地下水渗流作用下的滑坡稳定性进行了研究。如:Morgenstern(1963)最早基于极限平衡法研究了不同水位变化对边坡安全系数的影响,Desai(1977)和Cousins(1978)分别通过极限平衡法研究渗透作用下边坡的稳定性;Iversion and Major(1986),Hodge and Freeze(1997)认为水对滑坡变形起重要作用;Lam et al.(1987)对饱和-非饱和土进行了论述,分析地下水复杂的流动渗流实例;章广成(2005)提出土水特征曲线的多项式约束优化模型,以赵树岭滑坡为例分析滑坡渗流场以及水位下降过程中的稳定性系数之间的规律;代科建(2019)研究库水在不同降速、极端降速叠加降雨、土体强度弱化以及不同渗透系数下滑坡渗流及稳定性变化规律;陈欢(2018)对三峡库区沟边上滑坡进行渗流分析和稳定性分析评价;林仕祥等(2009)通过对三峡水库区猴子石滑坡的渗流场分析从而进行滑坡稳定性计算得到水位消落速度越快,对滑坡稳定越不利;徐庆方(2019)通过求解滑坡的稳定渗流场,对滑坡稳定性分析评价,得到考虑渗流作用滑坡的稳定系数小于不考虑渗流作用下边坡的稳定系数。上述研究均揭示了地下水渗流对三峡库区边坡稳定的不利影响。
许多学者曾对赵树岭滑坡进行过相关研究:许忆(2016)基于塑性力学极限分析法求得赵树岭滑坡的稳定性系数,得到赵树岭滑坡总体稳定,但稳定性富裕度不高;范国荣(2019)采用GEO-slope和FLAC3D对该滑坡不同工况下的稳定性研究;罗红明等(2008)以赵树岭滑坡为例,分析了库水位涨落对库岸滑坡稳定性的影响,得到库水位上升时滑坡稳定性系数总体逐渐增大,同一库水位下,上升时的稳定性系数比下降时的稳定性系数大等结论;陶宏亮等(2008)通过对赵树岭滑坡特征的归纳总结,对其进行稳定性评价,得到在水位上升和暴雨情况下仍满足稳定性要求。本文基于前期对赵树岭滑坡的充分调查,结合地下水渗流作用下的稳定性研究所取得的经验和成果,对赵树岭滑坡在地下水渗流作用下的稳定性进行分析,从而得到赵树岭滑坡的稳定性,完成其稳定性评价。
1 滑坡渗流场和稳定性分析数值模拟理论方法
1.1 地下水渗流计算方法
三峡库区库水位在175~145 m波动。库水位上升时,初始库水位以上滑坡体处于非饱和状态,库水位以下滑体处于饱和状态,随着库水位上升,初始库水位以上滑体内孔隙水压力也逐渐增加,土体由非饱和变为饱和状态;库水位下降时,库水位以上滑坡体处于非饱和状态,库水位以下滑体处于饱和状态,随着库水位下降,滑体孔隙水压力也逐渐消散,土体由饱和变为非饱和状态,非饱和区土壤水的运动和饱和区水的运动相互联系,将两者统一起来即所谓饱和与非饱和问题(李红军和王旭,2009)。采用库水位h作为控制方程的因变量,建立各向异性的二维饱和-非饱和渗流控制方程。对于各向异性的岩土体来说,饱和-非饱和二维渗流的一般控制方程(张培文等,2003)可以表达为:
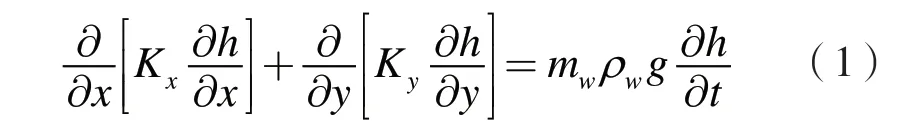
式中:ρw为水的密度;Kx,Ky分别表示水平方向和垂直方向的饱和渗透系数(本次模拟均假定Kx=Ky);g为重力加速度;m w为比水容量:定义为体积含水量θw对基质吸力(µa-µw)偏导数的负值,即:
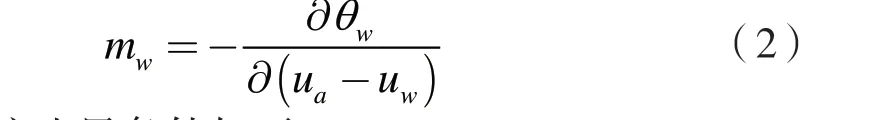
渗流边界条件如下:

1.2 滑坡稳定性计算方法
对于目前的滑坡稳定性计算,刚体极限平衡分析法是最为广泛的计算方法,包括Fellenius法(Fellenius,1957)、Bishop 法(Bishop,1995)、Janbu 法(Janbu,1973)、Morgenstern-Prince 法(Morgenstern and Price,1965)、Spencer法(Spencer,1967)、Sarma法(Sarma,1979)等。在本例中,赵树岭滑坡采用Morgenstern-Prince极限平衡法进行稳定性分析计算。该方法适用于不规则曲线形滑面的滑坡稳定性计算方法,在充分考虑条间力的相互作用下,先假定相邻两土条间的法向力和切向力之间存在函数关系,根据给出的边界条件,通过迭代求出解,水平力与垂直力之比用条间力函数f(x)与特定比例系数λ的乘积表示。计算时任一条块要满足静力和力矩平衡条件,误差较小。
采用GeoStudio软件进行模拟计算,利用SEEP/W模块模拟计算不同工况下滑坡区渗流场,用于分析土体或岩石等多孔材料饱和及非饱和地下水渗流和超孔隙水压力消散问题,进行传统的稳定状态饱和渗流场分析,以及随时间变化的瞬态饱和/非饱和渗流场分析。Seep/W模块的理论公式是基于饱和与非饱和土体渗流的达西定律,同样适用于非饱和土,区别在于非饱和条件下渗透系数不再是常数,而是随着含水量的变化而变化,并且间接地随着水压力的变化而变化。
2 赵树岭滑坡概况
三峡工程建设以来,在巴东县城拟建场地勘察过程中发现赵树岭一带的地形及地质结构与周围不协调,特对赵树岭滑坡进行了稳定性分析。赵树岭滑坡平面形态近似长方形(图1),前后缘南北向等长(约1200 m)、侧缘东西向等宽(570 m);坡面形态总体呈阶梯状,总体坡向340°~360°;滑坡后缘高程422~471 m,前缘涉水,高程58~115 m;滑坡纵长1130~1263 m,宽约565~585 m,厚24.8~110 m,平均厚度约70 m,总面积68.4×104m2,总体积约4788×104m3;滑坡主滑方向350°。

图1 赵树岭滑坡平面布置图
2.1 滑坡物质组成及结构特征
(1)滑体:赵树岭滑坡物质构成较复杂,滑体包括人工填土(Q4ml)、碎(块)石土(Qdel)、块石土(Qdel)、块石(Qdel)和块裂岩(Qdel)几个部分,表层一般为人工填土、碎块石土。
(2)滑带:滑带物质成分由粉质粘土夹碎石角砾构成。碎石表面有粉沫感,为碾压残余物质,局部见有残留擦痕,土体中分布有带擦痕的磨光镜面。碎石角砾成分由T2b3灰质岩或T2b2泥质粉砂岩构成,与滑床岩体相关联,局部有混杂现象。
(3)滑床:赵树岭滑坡滑床的岩性主要为T2b2、T2b3岩体。东侧滑体基床为T2b2泥岩,分布于滑坡中部及东区,深部基床为T2b3灰岩,分布于滑坡西侧及东部外侧缘。
2.2 滑坡水文地质特征
巴东县气候为亚热带季风气候,降雨主要集中在5—9月份,占全年降水量的2/3。该地区多年平均降雨量1100.7 mm,最大降雨量1522.4 mm,最小年降雨量694.8 mm。
赵树岭滑坡区内地下水按赋存条件大致可分为3类:第四系松散岩类孔隙水、基岩裂隙水和岩溶、溶隙水。水量均不丰沛,不具备范围较大的含水层。地下水在空间分布上具有很大的不均一性,在松散介质中大多为上层滞水,基岩中的裂隙水或岩溶、溶隙水多呈脉状。
2.3 滑坡变性特征分析
根据滑坡灾害调查情况,赵树岭滑坡在300 m高程以上的工程建设活动中未发现滑坡明显整体变形,300 m高程以下的平硐施工中也未见明显整体变形迹象。滑坡体内发现多处小型崩滑体,规模一般数百至数千立方米不等,塌滑体厚度一般小于10 m。这些崩滑变形有如下特征:(1)发生时代新,大多是近几年内产生的;(2)多为浅层局部土体崩滑;(3)其成因多与地形坡度、人工开挖及降雨有关。
3 滑坡地下水渗流分析
3.1 计算模型
选取滑坡主剖面建立地质模型,在补充勘查的5个纵向地质剖面中,根据两级滑坡分布的情况,选择c-c′剖面进行分析计算。将滑坡地质模型概化为滑体、滑带和基岩三部分,其中滑坡后部为碎块石土(Q4),前部为碎裂岩,碎裂体分为上下两部分,上部(碎裂岩1)为夹有大量碎块石土的泥岩、粉砂岩(T2b2);下部(碎裂岩2)以灰岩、泥灰岩(T2b3)为主要成分(图2a)。
渗流计算网格剖分采用四边形/三角形单元,共剖分成6678个节点、6741个单元(图2b)。

图2 赵树岭滑坡稳定性计算地质模型
3.2 边界条件和计算参数
渗流模拟中,在滑体表面175 m高程以下设为定水头边界,水头随工况变化;滑体表面175 m高程以上至滑坡后缘设为降雨入渗边界,流量随时间变化边界;基岩与滑带的接触面设为隔水边界,即零流量边界,边界条件如图3所示。

图3 模型边界条件
计算参数主要根据勘察成果以及结合该地区相似地质结构的滑坡岩土体参数进行工程地质类比反演综合确定,具体参数见表1,测得到各材料非饱和渗透特征曲线(图4)。

图4 不同岩土作用下水土特征曲线

表1 SEEP/W计算参数
3.3 渗流计算工况和计算结果
按照三峡库区水库运行情况,确定渗流计算模拟的4种基本工况,库水位145 m和175 m为稳水位工况;库水位175~145 m为库水位下降工况,降落速率为0.6 m/d;库水位175 m 叠加非汛期50年一遇5日暴雨工况。
工况①:库水位145 m,定水头边界,滑坡体内稳定性渗流场如图5,145 m库水位时,滑坡前部地下水浸润线靠近滑带侧逐渐升高,中部地下水浸润线亦呈现顺坡向缓倾。工况②:库水位175 m,定水头边界(正常水位),滑坡体内稳定性渗流场如图6,滑坡前部地下水浸润线与库水位贯通、持平,中部水位线平缓。工况③:库水位175 m降至145 m,库水位175 m稳态渗流场为初始状态,水头从175 m降至145 m(速率0.6 m/d),库水位下降过程地下水浸润线如图7所示,50天后渗流场如图8所示。库水位降落过程中,由于滑体渗透性良好,在坡体内产生了指向坡外的孔隙水压力,这种朝向坡外的瞬态动水压力不利于滑坡稳定。工况④:175 m库水位条件,叠加当地50年一遇5日暴雨量315.9 mm。以库水位175 m的稳态渗流场为初始状态,模拟结果显示(图9),滑坡前部地下水浸润线靠近滑带侧逐渐升高,中部地下水浸润线顺坡向缓倾。
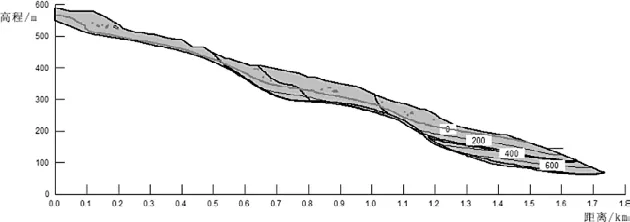
图5 工况①稳态渗流场

图6 库水位为175 m时滑坡体内稳态渗流场

图7 库水位下降过程地下水浸润线

图8 50天后渗流场

图9 暴雨+175 m库水位50天后渗流场
4 滑坡稳定性计算
利用Slope/W模块,采用Morgenstern-Price(M-P)法计算滑坡在不同工况下的稳定系数,计算主滑坡(滑坡整体)稳定性系数。滑坡稳定性判别,采用通常的分级标准即整体稳定(Fs≧1.10)、基本稳定(1.1>Fs≧1.05)、欠稳定(稳定性差 1.05>Fs≧1.0)、不稳定(Fs<1.0)四种状态。计算模型与渗流计算采用相同的计算剖面,即C-C′地质剖面,计算条块划分见图10。
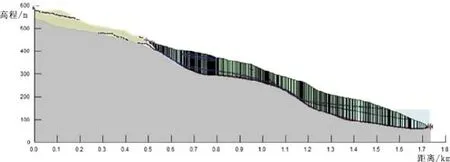
图10 SLOPE/W中赵树岭滑坡整体稳定性条分模型
滑坡稳定性计算采用的水位主变动情况与渗流计算相同,考虑近年来巴东县城及周边多次发生地震的情况,稳定性分析中加入地震影响计算,共计算6种工况,见表2。根据室内试验、现场实验、工程勘察资料等,赵树岭滑坡计算岩土体参数见表3。对赵树岭滑坡的稳定性计算结果进行汇总,结果见表4。
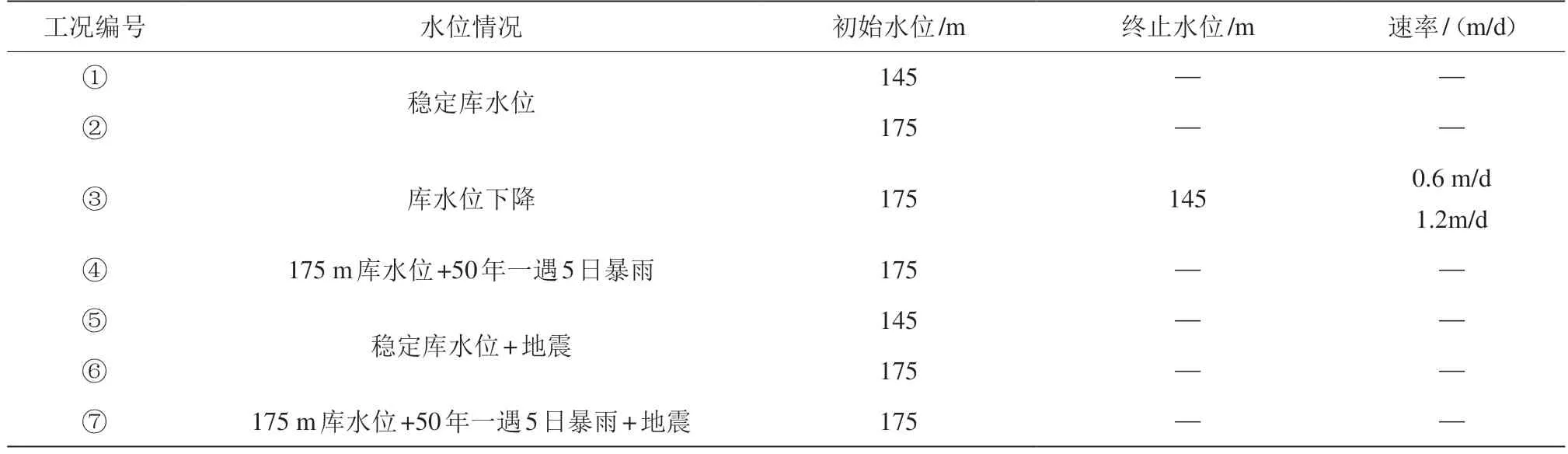
表2 稳定性计算工况

表3 赵树岭滑坡岩土体强度参数取值
在工况③组合中,库水位从175 m下降至145 m过程中,滑坡稳定系数随着库水位的不断下降而减小,且库水位以速度1.2 m/d下降时,其稳定性比0.6 m/d的情况下略有降低,但滑坡整体仍保持稳定。工况④库水位175 m时叠加5日暴雨,如果将降雨作用持续,Fs也表现出随时间呈现逐渐减小的变化特征,但持续降雨5天的情况下,滑坡仍处于稳定状态。工况⑤⑥,考虑地震烈度6度(地震作用水平荷载系数0.1)时,可得到地震作用将显著降低滑坡的稳定性,滑坡能处于基本稳定状态。工况⑦175 m库水位+50年一遇5日暴雨+地震,滑坡稳定性进一步降低,滑坡能处于基本稳定状态。
5 结论
通过上述稳定性计算得出以下结论:
(1)赵树岭滑坡整体是稳定的,在各种计算工况下,滑坡的稳定系数均大于1.0。从稳定系数计算的数值上看,降雨对滑坡稳定性的影响小于水位变动对滑坡稳定性的影响。
(2)库水位稳定的前提下,175 m水位时滑坡的稳定系数大于145 m水位条件下的稳定系数,原因可能与高库水位的水库压脚作用、和高水位时渗流压力作用小有关。库水位从稳定的175 m水位降到145 m水位并稳定的过程中,随着水位开始下降,滑坡稳定系数明显降低,大致在水位下降7~10天时达到最低,然后稳定系数逐渐增加,并趋于稳定。
(3)巴东县城区处于Ⅵ度地震区内,滑坡稳定性计算结果表明,地震作用是对滑坡稳定性影响最大的地质作用,考虑地震作用,赵树岭滑坡的稳定性显著降低,赵树岭滑坡由稳定状态转为基本稳定至欠稳定状态。
综上所述,滑移极限平衡分析的结果与赵树岭滑坡的实际情况基本相符,计算过程中降低了岩块的作用,加大了渗流压力作用。结合监测分析,赵树岭滑坡现状整体稳定,目前没有整体变形迹象,也无局部较大规模变形迹象和局部变形迹象,滑坡可以参考稳定性计算按照适宜性和分区原则规划建设使用。
