一种基于EMD-BLS的三相整流电路故障诊断方法

曾超俊，王荣杰,，王亦春,，郜怀通，林安辉,，韩 冉

(1.集美大学轮机工程学院，福建 厦门 361021；2.福建省船舶与海洋工程重点实验室，福建 厦门 361021)

0 引言

三相整流电路在实际运行中，开关器件通常会发生开路和短路两种常见故障。准确识别三相整流电路故障对于电力系统的安全运行和避免灾难性事故极其重要[1-3]。三相整流电路故障诊断的关键有二：一是提取反映整流电路状态的特征信息，二是对特征信息进行分类实现故障诊断[4]。

目前故障特征提取方法主要有[5-7]：小波变换(wavelet transform，WT)、主成分分析(principal component analysis，PCA)、奇异值分解(singular value decomposition，SVD)和经验模态分解(empirical mode decomposition，EMD)等。小波变换时频分析方法可处理时变的非平稳信号，但无法提取反映信号非线性的信息，分解的信号容易产生虚假频率[8]；主成分分析法提取特征完全无参数限制，但解释其自身含义总是具有一定的不确定模糊性，提取出来的特征不如原始样本完整，贡献率小的主成分可能是整体差异的重要信息；奇异值分解法能在特征提取时去除噪声，但是只适用于数值型，对非方阵数据分解出的数据具有高不确定性[9]；而EMD突破了传统时频分析的局限，并且在非平稳信号上表现良好，与传统的时频分析方法相比，EMD具有自适应性、正交性和完整性的典型特征。

应用于三相整流电路故障类型分类的方法主要有[10-13]：反向传播神经网络(backpropagation neural network，BP)、概率神经网络(probabilistic neural network，PNN)、支持向量机(support vector machines，SVM)、极限学习机(extreme learning machine，ELM)和宽度学习系统(broad learning system，BLS)等。反向传播网络因具有自学习能力被广泛推崇，但经常陷入局部最优和网络训练能力差且收敛速度慢等困境；概率神经网络虽然克服了反向传播网络训练差收敛慢的缺点，但计算复杂度高且样本要求也高[14]；支持向量机在多分类问题上存在无法达到高精度分类的困难，且求解分类问题需要消耗大量的存储空间；极限学习机结构相对简单，但当调整极限学习机结构时，重新训练耗费时间相当长[15]；而宽度学习系统结构简单，可以通过增加映射节点和增强节点数目来提高性能，是为各种应用的快速通用逼近而设计的。

因此，本文将揭示故障本质局部特征的经验模态分解和计算复杂度低的宽度学习系统相结合，应用于三相整流电路故障诊断中。

1 故障诊断方法的建立

1.1 经验模态分解

经验模态分解采用黄锷于1998年提出的自适应信号分析方法[16]。EMD可以逐步分解信号并产生一系列固有模式函数(IMF)和1个残差余项的和，每1个IMF的获取均依赖于信号的局部时间尺度，不利用任何其他信息。EMD的分解可以归纳为以下4个步骤。

步骤1：找出信号x(t)中的所有局部极大值和极小值点，再分别用曲线把所有极大值点和所有极小值点连接起来，得到信号x(t)的上包络线fmax(t)和下包络线fmin(t)。与此同时把上包络线和下包络线的平均值用m(t)表示[17]。

步骤2：设x(t)与m(t)的差记为h1(t)，即

h1(t)=x(t)-m(t)。

(1)

理想条件下，h1(t)是一个基本模式分量(IMF)。但是，实际环境下信号是复杂多变的，得到的差h1(t)中可能仍然存在非对称波。因此将h1(t)当成新的x(t)，重复步骤1和2的操作，直至h1(t)为一个基本模式分量，记为

c1(t)=h1(t)。

(2)

步骤3：分解获得第一个基本模式分量c1(t)后，用x(t)减去c1(t)得到余下的信号x1(t)，则

x1(t)=x(t)-c1(t)。

(3)

步骤4：把x1(t)当做新的x(t)，重复以上3个步骤，多次分解得到

(4)

直至满足筛选过程的极限停止准则，这一般是通过限制h1(k-1)(t)和h1k(t)之间的标准差δ的大小来确定：

(5)

其中：T表示信号时间跨度；标准差δ一般取0.2～0.3。最后停止条件下残余的项xn(t)=rn(t)，就是原始信号分解后留下的残差。通过EMD分解，整个信号x(t)被分解成若干个基本模态分量ci(t),i=1,2,…,n，和一个残差余项rn(t)的和，即

(6)

1.2 宽度学习系统

BLS[18-20]是由澳门大学陈俊龙教授团队于2018年提出的一种替代深度学习网络的方法。它是将映射特征用作随机矢量函数链接神经网络(RVFLLNN)输入的想法进行设计的。BLS可以用高效的方式对新加入的数据进行更新(输入的增量学习)。BLS通过建立特征节点和增强节点，来执行大数据的特征提取和降维，用于更新RVFLNN中的输出权重，即新增加的输入数据和新添加的增强节点的输出权重，以保持系统的有效性。

BLS结构图如图1所示，假设给出输入数据X和增强节点δi(XWei+βei)，则它们成为第i个映射特征Zi，其中Wei和βei是具有适当维数的随机权重。令Zi=[Z1,…,Zi]，这是所有前i组映射特性的串联。同样，将第j组增强节点ξj(ZiWhj+βhj)表示为Hj，所有前j组增强节点的连接表示为Hj=[H1,…,Hj]。

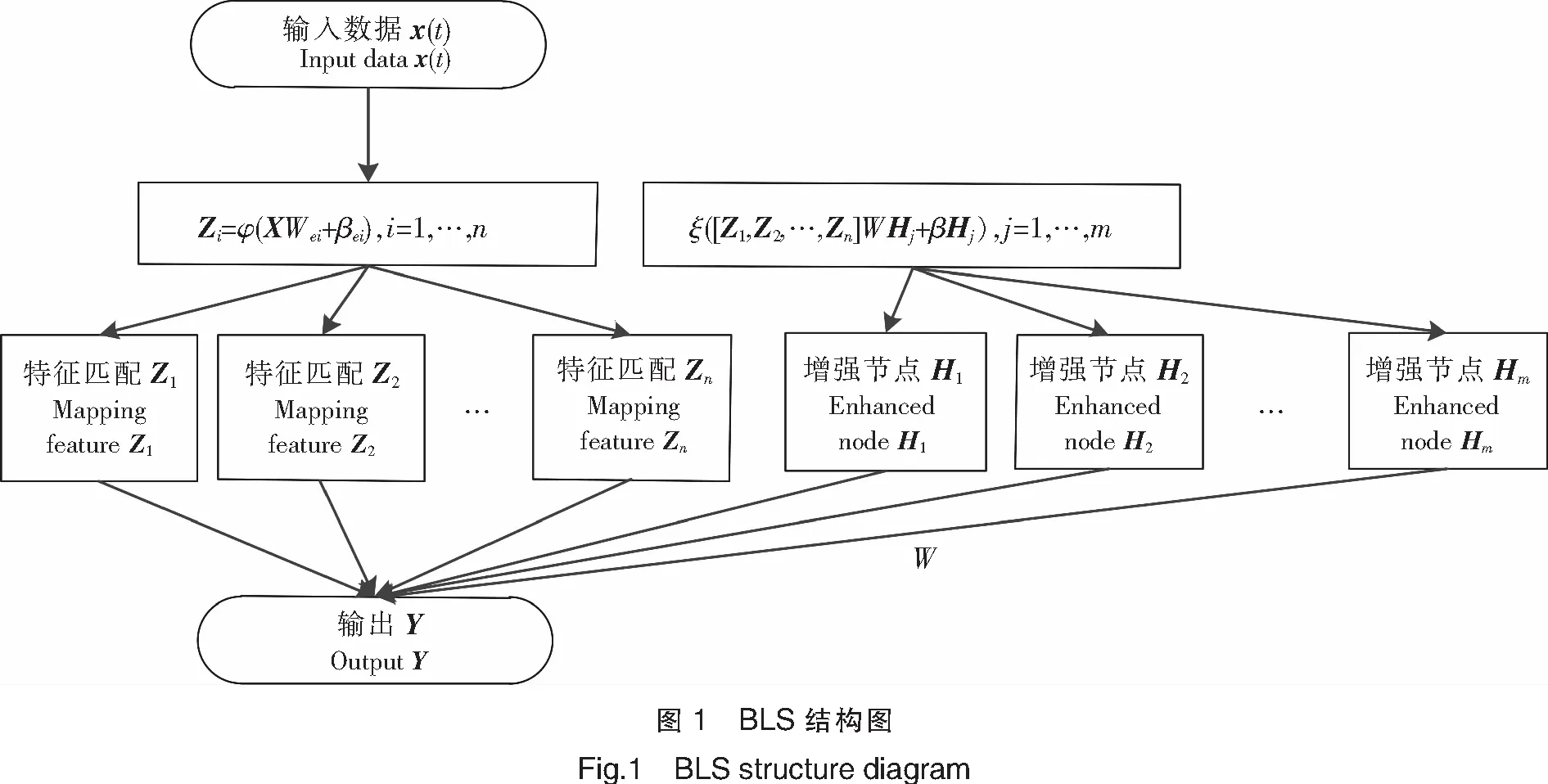
在宽度学习系统中，对初始Wei进行微调以获取更好的特征。假设输入数据集X有N个样本，每个样本有M个维度，Y是输出矩阵且属于RN×C[21]。对于N个特征映射，每个映射生成k个节点，可以表示为：

zi=φ(XWei+βei),i=1,…,n。

(7)

其中Wei和βei是随机生成的。令所有特征节点Zn≡[Z1,…,Zn]，则第m组增强节点可表示为：

Hm≡ξ(ZnWhm+βhm)。

(8)

因此，BLS可以表示为

Y=[Z1,…,Zn|ξ(ZnWh1+βh1),…,ξ(ZnWhm+βhm)]Wm=

[Zn|Hm]Wm。

(9)

其中，Wm代表输出层的权重。

对于一个输入系统x(k)：

X(k)=[x1,x2,…,xm]。

(10)

则它的增强节点

H=ξ(W1X+b1)，

(11)

它的宽度神经网络的输出

Y=W2·[X|H]。

(12)

其中:m代表不同的尺度长，这是人为设定的常数；W和b是随机输入权重；ξ是增强节点函数。

1.3 三相整流电路故障分析

为了验证所提出的EMD-BLS故障诊断方法的有效性，在Simulink仿真实验平台上模拟三相整流电路，分析出现的故障，仿真模型如图2所示。在整个运行过程中，晶闸管故障表现极其明显。

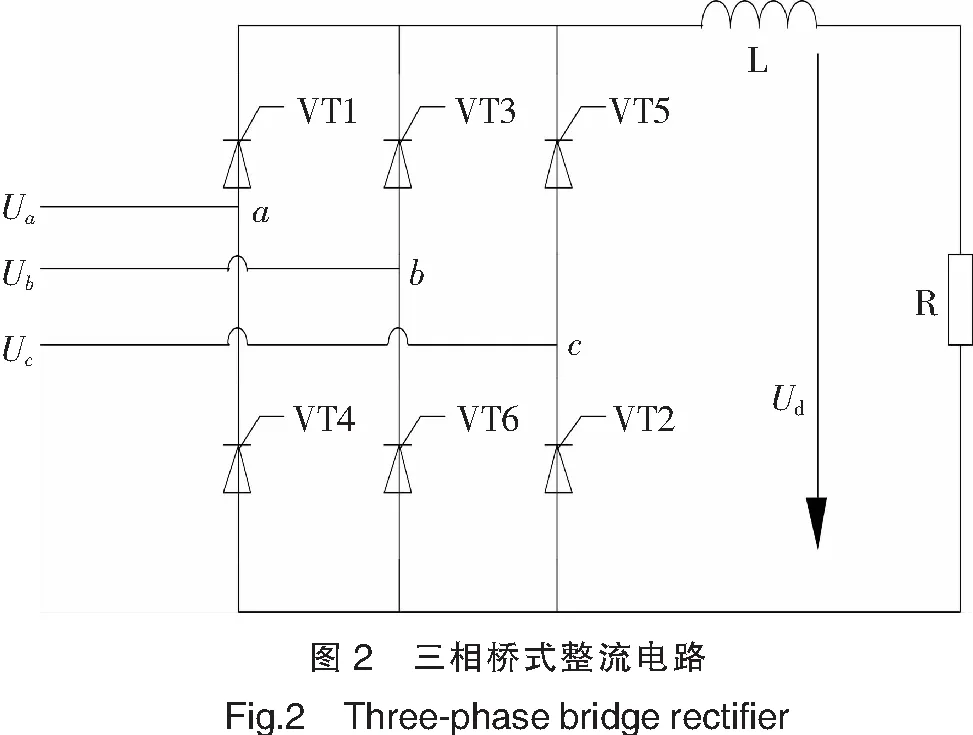
本文对晶闸管故障进行研究，将晶闸管开路和短路作为晶闸管故障，以晶闸管不正常工作为基准，把故障分成六大类：

1)晶闸管无故障；

2)只有一个晶闸管发生故障，即VT1、VT2、VT3、VT4、VT5和VT6之中有一个发生故障；

3)只有一个晶闸管发生短路故障，即VT1、VT2、VT3、VT4、VT5和VT6之中有一个发生短路故障；

4)同相不同组的两只晶闸管同时发生开路故障，即VT1和VT4、VT2和VT5、VT3和VT6同时发生开路故障；

5)同组不同相的两晶闸管同时发生故障，即VT1和VT3、VT1和VT5、VT3和VT5、VT2和VT4、VT4和VT6、VT6和VT2同时故障；

6)不同组不同相的两晶闸管同时发生开路故障，即VT1和VT2、VT2和VT3、VT5和VT6、VT1和VT6、VT3和VT4、VT5和VT4同时故障。

共计28种故障。

1.4 故障诊断流程

基于EMD-BLS的三相整流电路故障诊断方法的流程图如图3所示。首先对三相整流电路开关器件信号进行EMD分解，得到一系列基本模式分量(IMF)，构成特征矩阵；然后把所得特征提取值输入BLS模型，对输入特征数据进行线性变换，形成BLS的特征节点，通过非线性变换使特征节点随机生成一个增强节点[22];再将所有的映射特性和增强节点都直接连接到输出，通过伪代码得到相应输出的权重，在得到输出权重后，进行训练并输出结果。

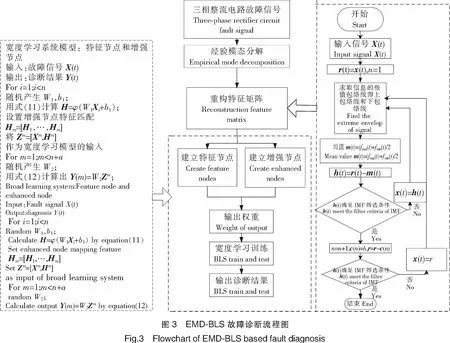
BLS极大地缩短了计算时间，而且可以通过快速的增量学习来扩展网络结构，而无需进行全面完整的再次网络训练。

2 实验结果与分析

2.1 特征提取方法比较

为了验证基于EMD分解的特征提取效果，将EMD与小波变换、主成分分析方法和奇异值分解法三种特征提取法得到的特征输入BLS进行训练测试比较。

2.1.1小波变换

如式(13)，将信号分解成一系列小波函数的叠加，信号的局部特征用小波函数来逼近，把基波函数ψ(t)经过位移τ后，在不同尺度a下的待分析的信号f(t)做内积[23]，有：

(13)

2.1.2主成分分析

(14)

(15)

(16)

Cu=λu，

(17)

(18)

2.1.3奇异值分解

奇异值分解如式(19)[25]为

A=UΣV′。

(19)

其中：矩阵A是一个m×n的矩阵;U是一个m×m的矩阵；Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值；V是一个n×n的矩阵；U和V都是酉矩阵，即满足U′U=I，V′V=I。

将得到的特征矩阵输入到BLS网络中进行训练比较。BLS的特征节点和增强节点都相同，经过10次实验得到3种不同触发角的实验结果(如表1所示)，NONE为未进行特征提取的原始数据。

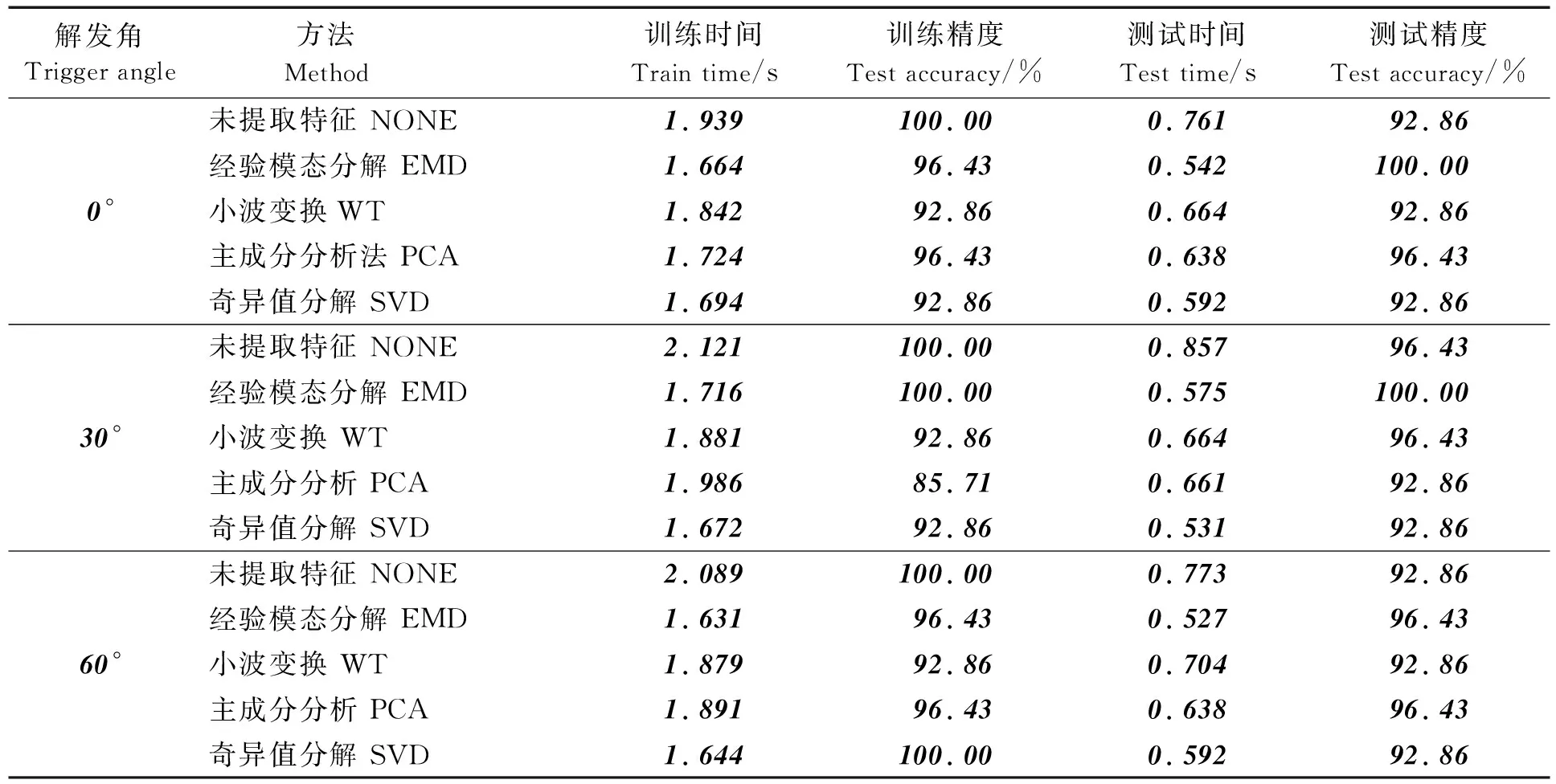
表1 触发角为0°、30°、60°时不同特征提取方法的比较

由表1可看出，当触发角为0°、30°和60°时，与没有特征提取的原始数据进行比较，应用特征提取方法能有效地减少训练时间和提高准确度。0°和30°时EMD的特征提取效果明显，测试精度达到100%，在这四种特征提取方法中的表现是最好的。当触发角为30°时，虽然利用SVD进行特征提取可以有效提高训练时间，但其测试精度为92.86%，而EMD方法为100%；同时，与WT、PCA提取的特征数据相比较，EMD方法可以有效地减少训练时间和测试时间，提高特征提取的稳定性。当触发角为60°时，用EMD方法提取的训练时间和测试时间都要比WT、PCA和SVD少，而且在一定程度上还提高了测试精度。综上所述， EMD方法能较好地去除数据之间的冗余，保持数据的有效性，相比其他方法对提高BLS模型的分类准确率更有效。

2.2 故障分类方法的比较

为了验证EMD-BLS故障诊断方法的有效性，把用EMD提取后的数据输入到不同的分类器中进行比较，即与EMD-ELM、EMD-BP、EMD-PNN、EMD-SVM共4种故障诊断方法进行比较。ELM、BP、SVM的隐藏层选择Sigmoid函数，BLS的增强层选择Sigmoid函数。同时，从间隔[-1,1]上的标准均匀分布中提取BLS中特征节点层和增强节点层的权重和偏移量。此外，实验结果用每种方法得到的10次平均值描述。三种不同触发角的故障分类实验结果分别见表2。

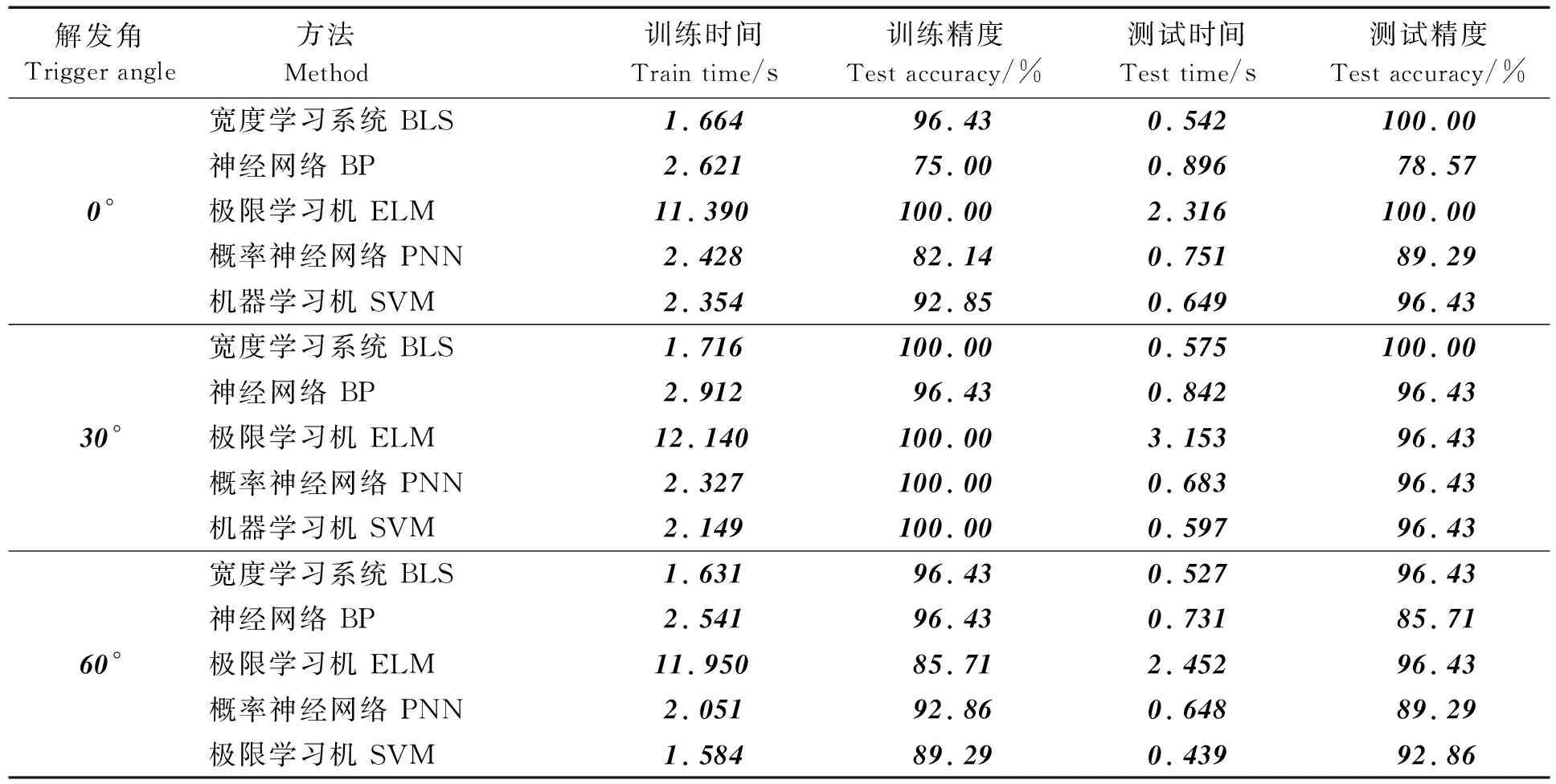
表2 触发角为0°、30°、60°时不同分类方法的比较

由表2可以看出：当触发角为0°时，ELM在训练和测试过程中表现出很好的准确性，训练准确率为100%，测试准确率为100%，但其训练时间和测试时间远远多于其他分类模型；BLS模型的训练时间仅需1.664s，优于ELM、BP、PNN、SVM的训练时间。当触发角为30°时，5种分类方法都能获得较高的训练精度和测试精度， 其中BLS的训练时间和测试时间分别只需要1.716s和0.575s，分别低于ELM、BP和PNN、SVM。当触发角为60°时，SVM方法可以更快地实现故障诊断，训练和测试最快，但是训练精度和测试精度比BLS更低；BLS模型应用于故障分类，训练准确率和测试准确率均为96.43%，分类精度优于其他分类模型。综上所述，三相整流电路经EMD分解特征提取后，用BLS分类与用ELM、BP、 PNN、SVM分类相比，BLS能够相对较快精准地完成分类，在不同的故障数据类型下可以以最好的测试精度实现故障诊断。

3 结论

本文提出一种基于EMD-BLS的三相整流电路故障诊断方法，利用EMD方法提取特征，获得低维特征矩阵，再将提取后的数据输入BLS模型，实现故障诊断。经过MATLAB仿真实验，EMD特征提取方法效果较好，BLS分类迅速准确，EMD-BLS方法能有效地实现故障诊断。