基于改进型A＊-蚁群混合算法的USV 航迹规划

孙海文，肖玉杰，王生玉

(1.中国人民解放军91054 部队，北京 102442；2.海军航空大学，山东 青岛 266000)

0 引言

航迹规划[1]是USV 研究领域中最主要的研究方向之一。USV 航迹规划指规划出一条安全快速到达目标位置的路径。

航迹规划主要研究避障问题。目前，传统的航迹规划算法有模拟退火算法[2]、禁忌搜索算法[3]、A*算法[4]、人工视场法[5–6]等。随着智能仿生学算法的发展和应用，逐渐将遗传算法[7]、粒子群算法[8]以及蚁群算法[9]等用于航迹规划。其中，A*算法具有较强的全局搜索能力，在低密度避障环境中能够快速高效地规划出到达目标点的合理路径，但当避障环境密度较高时，A*算法容易陷入局部死区。蚁群算法具有较强的鲁棒性，在高密度环境下亦能找到合理路径，但其收敛速度较慢。因此本文将水面环境进行分割，在高密度环境中设置过度目标点，在低密度环境下采用A*算法进行航路规划，当目标到达过度目标点，则采用蚁群算法进行搜索规划航路。从而提高了USV 全局和局部航路规划能力。

1 航行环境模型

栅格（grid）法[1]，即用编码的栅格来表示地图，把包含障碍物的栅格标记为障碍栅格，反之则为自由栅格，以此为基础作路径搜索。栅格法是目前研究最为广泛的空间规划方法。构建路径规划环境，令障碍物的栅格状态为1，自由栅格状态为0。环境矩阵为：

模拟空间环境如图1 所示。

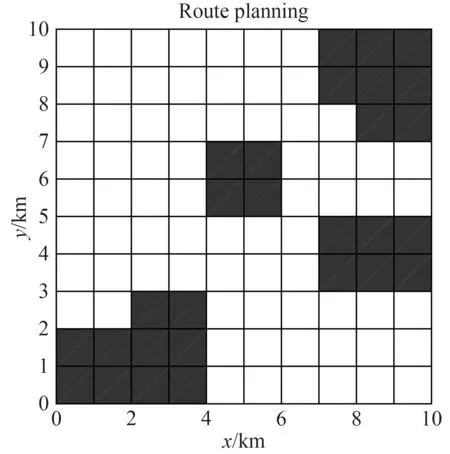
图1 模拟的空间环境Fig.1 Simulated space environment

无人航行器节点的位置移动方式如图2 所示。

图2 位置移动模式Fig.2 Position movement mode

2 改进型A*-蚁群混合算法

2.1 启发式A＊算法

A*算法[4]的估价函数为：

式中：f(n)为当前USV 所处的节点n的总代价；g(n,s)为节点n到起始节点s的实际代价函数；h(n,e)为节点n到目标节点e的预估代价函数。

2.2 改进型蚁群算法

在传统的蚁群算法[10–11]中，当所有蚂蚁完成一次迭代后，对路径上(i,j)上的信息量进行调整，调整公式：

式中：τij(t+n)表示t+n时刻路径 (i,j)上的信息浓度；ρ表示信息素挥发系数；1-ρ 表示信息素残留因子；Δτij(t)表示本次循环中所有蚂蚁在路径 (i,j)上释放的信息素浓度之和；Q为一常数；Lk表示第k只蚂蚁在本次循环中所走的总路径长度。

为增强蚁群算法的快速性和有效性，本次改进了信息素的更新模型，增强了可行路径中最优路径的信息浓度，减弱了最差路径的信息浓度，并通过调整信息素浓度总和比例，增强算法的寻优能力。

式中：Lmin表示第k只蚂蚁在所经历的迭代中可行路径的最小值；Lmax表示第k只蚂蚁在所经历的迭代中可行路径的最大值。

2.3 改进型A＊-蚁群混合算法

USV的航路规划分为全局规划和局部规划。算法首先利用A*算法进行全局规划，当遇到高密度环境，则采用蚁群算法，通过蚁群信息素搜索原理，进行障碍的规避。

根据环境栅格图的特点在高密度局部图中设置过渡节点，过渡节点的总代价函数要小于USV 所处节点的代价。目标先采用A*算法朝向目标节点进行全局规划，到达过渡节点时采用蚁群搜索算法进行局部规划。在USV的全局航行过程中，不断采用蚁群算法进行局部高密度避障在，可有效地提高航行器在复杂环境中的航路规划能力，避免陷入局部死锁。算法流程如图3 所示。

图3 改进的A*-蚂蚁混合算法流程图Fig.3 Flow chart of improved A * -ant hybrid algorithm

3 仿真实验

为了验证本文所提改进型A*-蚁群混合算法的有效性和优势性，进行仿真实验比较。

3.1 低密度简单环境下的仿真比较分析

本仿真试验选取22 km×22 km的正方形水域，采用栅格法划分该区域为22×22的网格，各网格表示1 km×1 km 区域。黑色表示障碍物区或禁航区，白色表示自由航行区。分别采用传统A*算法、蚁群算法、改进型蚁群算法、改进型A*-蚁群混合算法进行航路规划。蚁群规模为M=50，最大迭代次数为N=100；信息素重要程度因子α=1；启发函数重要程度因子β=5；常系数Q=2 000；信息素挥发因子为ρ=0.7；单位栅格边长为1 km。仿真结果如图4 所示。

图4 四种算法的仿真结果Fig.4 Simulation results of four algorithms

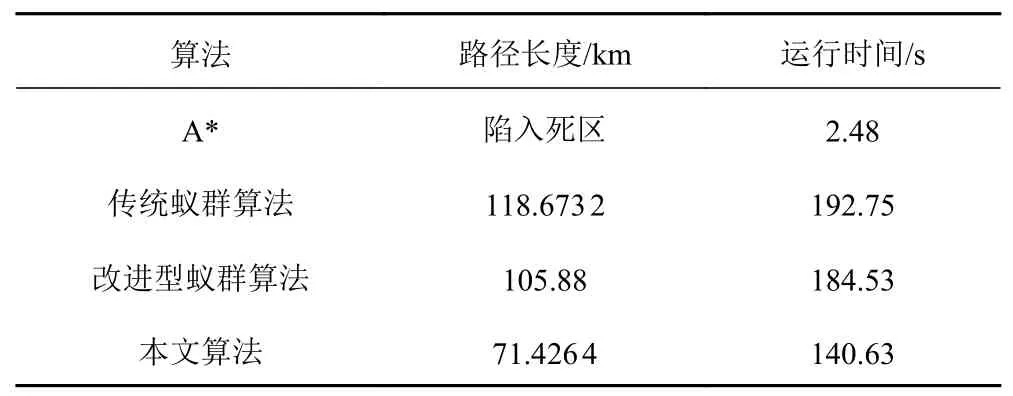
图4 中的路线规划路径长度和运行时间统计如表1所示。

表1 四种算法的数据统计Tab.1 Data statistics of four algorithms

根据图4 和表1 比较分析，4 种方法的路径长度比较为改进型蚁群算法<本文算法

3.2 高密度复杂环境下仿真比较分析

为了进一步证明该算法的优越性和有效性。选取面积为45 km×45 km的正方形水域，采用栅格法将面积划分为45×45 个网格，每个网格代表1 km×1 km的面积。分别采用传统A*算法、蚁群算法、改进型蚁群算法、改进型A*-蚁群混合算法进行航路规划。仿真参数不变，增加了障碍的复杂性。仿真结果如图5 所示。

图5 中的路线规划路径长度和运行时间统计如表2所示。

根据图5 和表2的比较分析，4 种方法的路径长度比较为：本文算法<改进型蚁群算法<传统蚁群算法

图5 四种算法的仿真结果Fig.5 Simulation results of four algorithms

表2 四种算法的数据统计Tab.2 Data statistics of four algorithms

仿真结果表明，A*算法在低密度、小规模环境下具有较强的路径规划能力和较短的运行时间。然而，在高密度、复杂的环境中，A*算法容易陷入死区。与传统蚁群算法和A*算法相比，本文提出的算法大大提高了路径规划的质量和效率，能够快速有效地完成OSV的路径规划。

4 结语

针对高密度复杂环境下的无人水面航行器（USV）航迹规划问题，本算法有效地增强USV 航迹规划能力，解决了传统蚁群算法和A*算法各自使用不能兼顾全局和局部规划的问题。通过仿真比较分析，本算法能够有效地平衡全局和局部规划，提高在复杂环境下的USV 航迹规划能力。本文方法将为USV 大规模复杂的环境任务提供研究依据。