港口船舶系泊载荷参数化及特性研究

赵奎，魏志强，魏立明，贺保卫，崔海朋，杜鹏

(1.中国海洋大学 信息科学与工程学院，山东 青岛 266100；2.青岛杰瑞工控技术有限公司，山东 青岛 266061；3.中船重工（青岛）海洋装备研究院有限责任公司，山东 青岛 266061)

0 引言

船舶大型化、智慧化发展及大型深水开敞式港口码头的现代化建设，使得船舶港口系泊问题受到业界广泛关注和研究。船舶与码头大多采用旁靠方式进行装卸作业，通过系泊缆与橡胶护舷相连[1]。船舶靠港系泊时受到风、浪、流多环境载荷联合作用[2–3]，导致其运动响应具有多变性和突发性[4]，由此关系到码头结构、船舶自身及装卸作业的安全性，及时有效地进行系泊动态响应分析，选择合适的靠泊方式、系缆绳索等对多方安全至关重要。

近年来，国内外学者针对船舶港口系泊过程的运动特性及环境载荷分析开展了大量的研究工作。SHASHIKALA[5]通过编写SHIPMOOR 程序，参数化计算了船舶系缆力，并通过试验验证了程序计算结果的有效性。KIM[6]采用时域方法研究了水动力干扰效应对不同系缆方式下的浮体系缆力影响。ROSA[7]研究发现恶劣海况下，仅依赖系泊缆绳对船舶大幅值运动的限制不足。贾德君等[2]应用时域响应方法，对比研究了不同环境载荷下，传统系泊与恒定范围张力系泊下的船舶系缆强度。孟祥玮等[8]提出了船舶系泊中波浪载荷理论计算公式，对我国现有规范进行了补充完善。张鼎等[9]采用时域计算方法分析了风、流载荷共同作用下系泊缆绳预张力、材质和系泊布置等对系泊系统的影响。刁峰等[10]通过建立系泊状态下船体与平整冰相互作用的二维数学模型，计算了极地钻井船系泊冰阻力、系泊力以及船体运动响应，试验结果表明该方法能够有效预报系泊载荷。骆寒冰等[11]采用谱分析方法，研究了涌浪环境下系泊起重船吊装组块耦合运动响应。陈里等[12]分析了内河港口滑坡涌浪作用下船舶系缆力和撞击能的影响因素，以及波高、水深等因素影响下船舶系缆力和撞击能的变化规律，得出了涌浪作用下船舶系缆力和船舶撞击能的经验计算式。

目前，国内船舶港口系泊载荷计算采用《港口工程载荷规范》[13]（JTS144-1-2010）的方法进行，基于该规范的船舶系泊静态理论计算的局限性，使得大型船舶在恶劣环境下系泊安全存在隐患，加之港口单位大多采用人工计算，效率较低，误差较大。此外，CFD 数值模拟和水池试验计算周期较长、费用较高，并往往简化了海洋环境的约束条件，对恶劣海况条件预估不足，使得计算结果存在一定偏差。因此，本文基于文献[13]通过港口气象水文采集传感器的数据输入，编程实现了船舶港口系泊缆力的动态参数化计算，并通过水池试验验证了该系统的有效性及可靠性，为船舶港口系泊运动响应快速分析提供了支撑，具有一定的工程实用价值。

1 船舶港口系泊载荷参数化

1.1 系泊缆力计算模型

船舶港内系泊缆力应综合考虑风、浪、流共同对船舶作用所产生的横向分力总和与纵向分力总和，如下式：

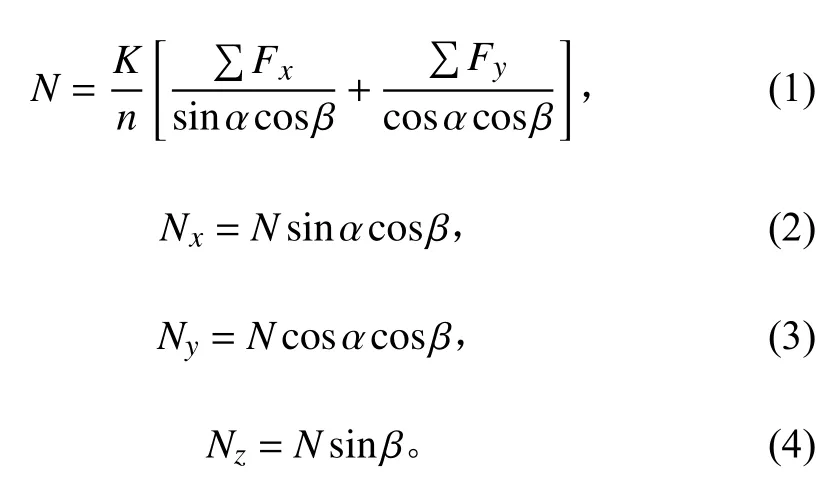
式中：N表示船舶港内系泊缆力，kN；Nx，Ny，Nz分别表示系泊缆力横向、纵向、竖向分力，kN；∑Fx、∑Fy分别表示风、浪、流对船舶共同作用产生的横向分力总和与纵向分力总和，kN；n表示系泊船舶同时受力的系船柱数目；K表示系船柱受力分布不均匀系数，n=2 时，K=1.2，n>2 时，K=1.3；α表示系船缆水平投影与码头前沿夹角，（°）；β表示系船缆与水平面间夹角，（°）。

1.2 风、浪、流载荷计算模型

1.2.1 风载荷计算模型

作用于船舶上的风载荷垂直于码头前沿的横向分力和平行于码头前沿的纵向分力可按式（5）和式（6）进行计算。

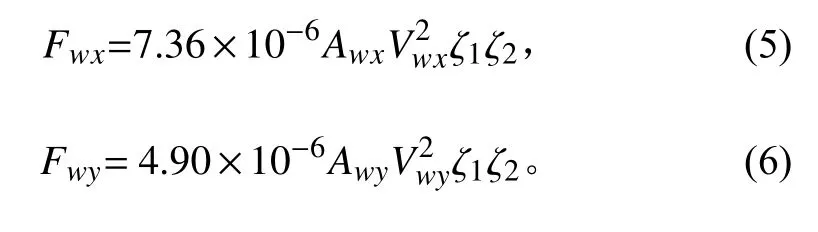
式中：Fwx，Fwy分别表示作用于船舶的风载荷横向分力和纵向分力，kN；Awx，Awy分别表示船体水面以上横向和纵向受风面积，m2；Vxy，Vwy分别表示风速的横向和纵向分量，m/s；ζ1表示风压不均匀折减系数；ζ2表示风压高度变化修正系数。

1.2.2 浪载荷计算模型

《港口工程载荷规范》中尚未给出波浪作用于船体的系缆力计算公式，本文基于文献[8]提出的船舶波浪产生的缆力载荷计算公式与方法，进行参数化计算。

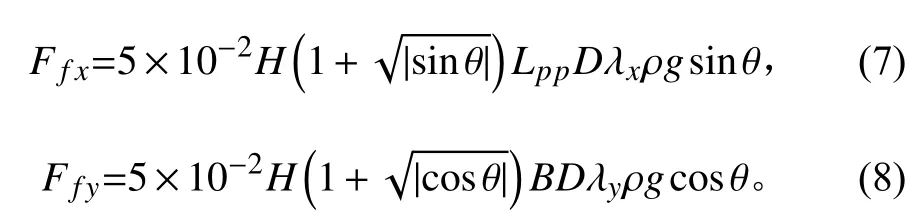
其中：

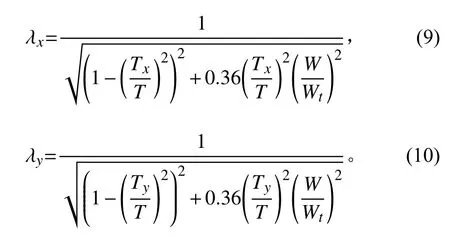
式中：Ffx，Ffy表示浪载荷沿船舶纵轴的横向分力和纵向分力，kN；H代表入射波高，m；θ为波浪入射角度，度；Lpp为船舶垂线间长，m；D为船舶吃水，m；B为船舶型宽，m；g为重力加速度，9.81 m/s2；Tx为船舶横摇周期，s；Ty为船舶纵摇周期，s；T为波浪周期，s；W为船舶当前排水量，t；Wt为船舶满载排水量，t。

1.2.3 流载荷计算模型

对于开敞式港口透空式系船，当流向与船舶纵轴夹角小于15°或大于165°时，沿船舶纵轴的流载荷船首横向分力、船尾横向分力、流载荷纵向分力可按下式计算：

式中：Fscx，Ffcx，Fcy分别表示沿船舶纵轴的流载荷船艏横向分力、船尾横向分力和纵向分力，kN；Cscx，Cfcx，Ccy分别表示流载荷船首横向分力系数、船尾横向分力系数和纵向分力系数；Vc表示水流速度，m/s；ρ表示水密度，t/m3；Bwl表示船舶水线以下横向投影面积，m2；Bf表示船舶水线以下湿表面积，m2。

对于开敞式港口透空式系船，当流向与船舶纵轴夹角为15°～165°时，沿船舶纵轴的流载荷横向分力与纵向分力可按下式计算：

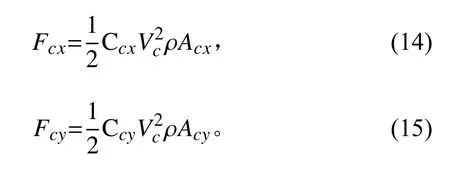
式中：Fcx，Fcy分别表示沿船舶纵轴的流载荷横向分力和纵向分力，kN；Ccx，Ccy分别表示流载荷横向分力系数和纵向分力系数；Acx，Acy分别船舶水下部分垂直和平行水流方向的投影面积，m2。

1.3 系泊载荷参数化程序设计

1.3.1 程序架构及流程

《港口工程载荷规范》系泊载荷计算主要包括风、流载荷内容，文献[8]进一步补充完善了波浪载荷对船舶系缆力的贡献，基于上述风、浪、流作用船舶后产生的系泊载荷计算方法，本程序架构如图1所示。

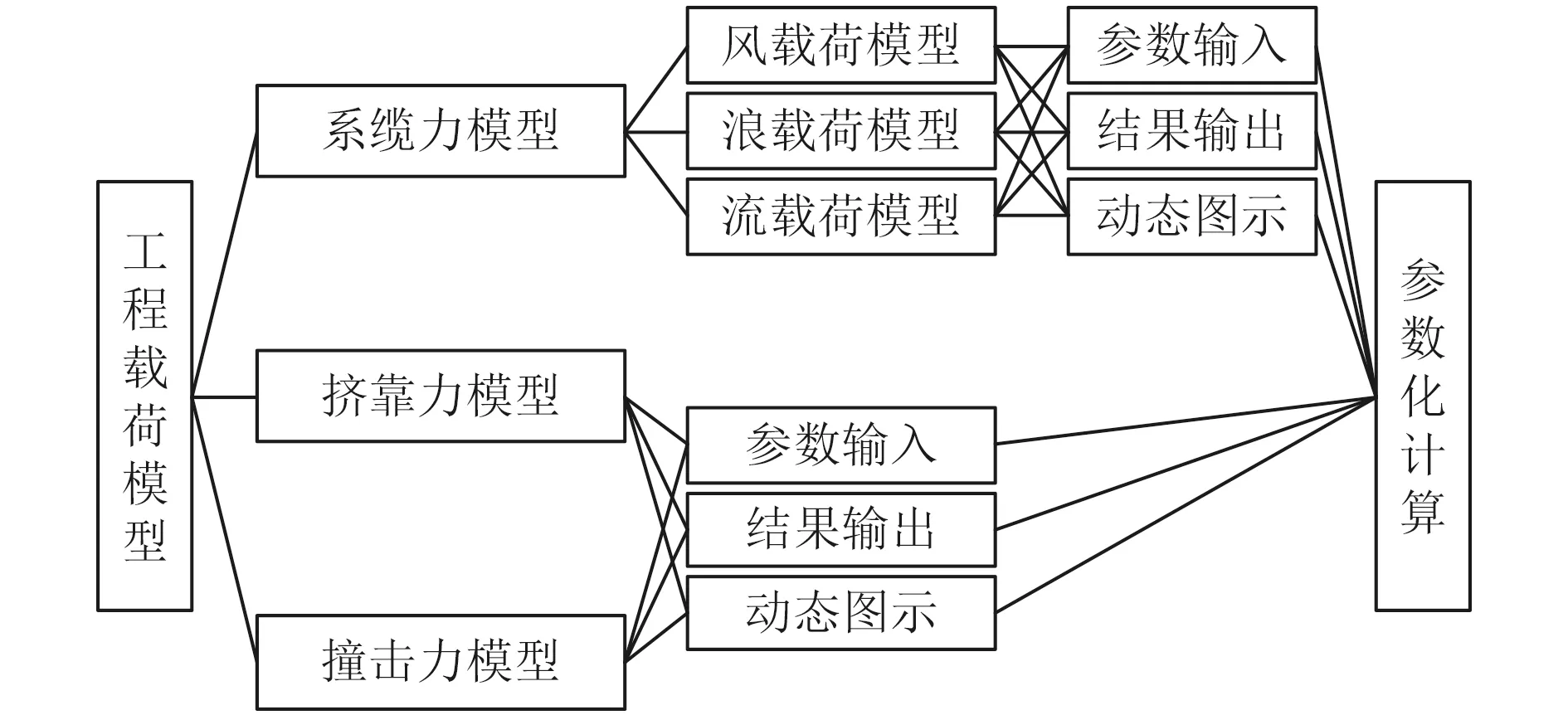
图1 系泊载荷计算程序架构Fig.1 Framework of mooring load calculation program

根据环境载荷、船舶主尺度、程序设置参数等因素，基于VB.net 开发环境，编程开发船舶系泊载荷计算程序，通过传感器实时采集风、浪、流数据无线传输至程序，计算设定时间步长内的环境数据平均值，进而动态求得船舶系泊时风、浪、流载荷贡献值，并将结果曲线动态绘制于界面右侧。计算流程如图2所示。

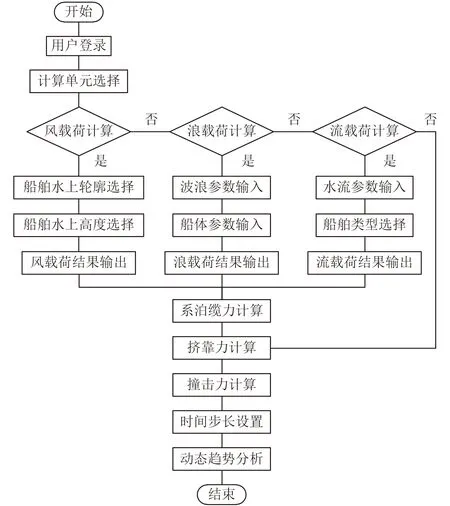
图2 系泊载荷计算流程图Fig.2 Flow chart of mooring load calculation

1.3.2 参数化界面

风、浪、流载荷经程序化计算后，可通过设置时间步长，实时显示当前环境参数，并将环境载荷趋势变化实时反映至界面中，以浪载荷计算为例，时间步长设置为1 h，其载荷实时计算结果趋势曲线如图3 所示，其他界面原理相同。

图3 浪载荷计算界面Fig.3 The interface of wave load calculation

2 船舶水池系泊试验

为验证该程序的可靠性、准确性及研究船舶系泊响应特性，通过船舶水池系泊试验进一步分析环境载荷对船舶系泊缆力的影响。

试验数据来源于大连理工大学船舶拖曳水池系泊试验数据[14]，水池长170 m，宽7 m，水深4 m；造波机由20 块造波板组成，最大造波高0.4 m；试验船型为中远海运集团2012 年建造的30000DWT 多用途重吊船，其主尺度如表1 所示，模型缩尺比为1∶30.18。试验时，室内温度为21.6 ℃，水运动粘性系数取值0.969×106m2/s。船体型线图如图4 所示，系泊船舶模型及系泊示意如图5 和图6 所示。

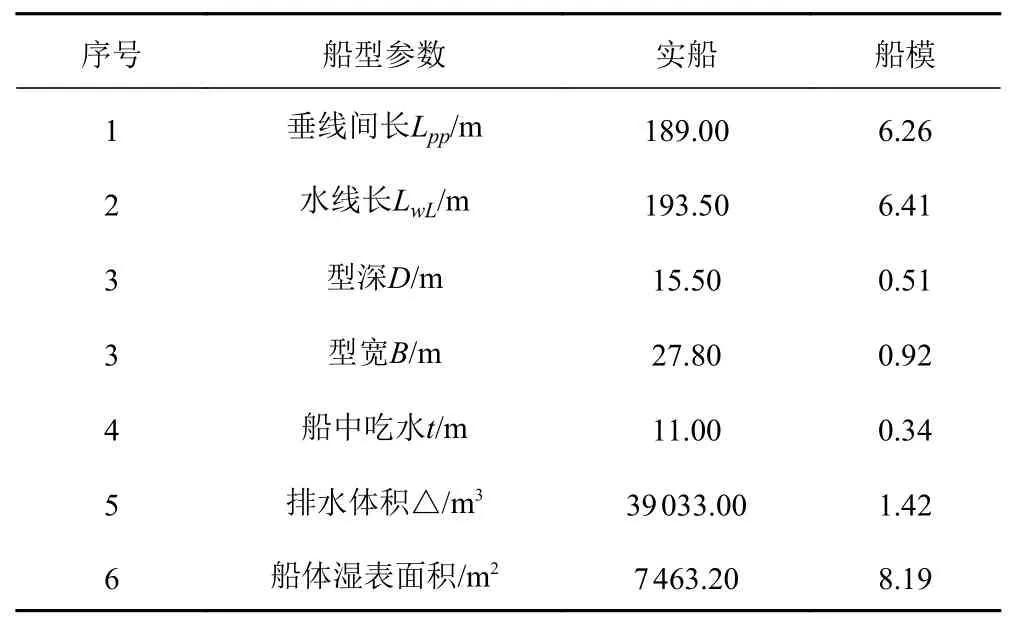
表1 船舶主尺度参数Tab.1 Principal dimension parameters of ship

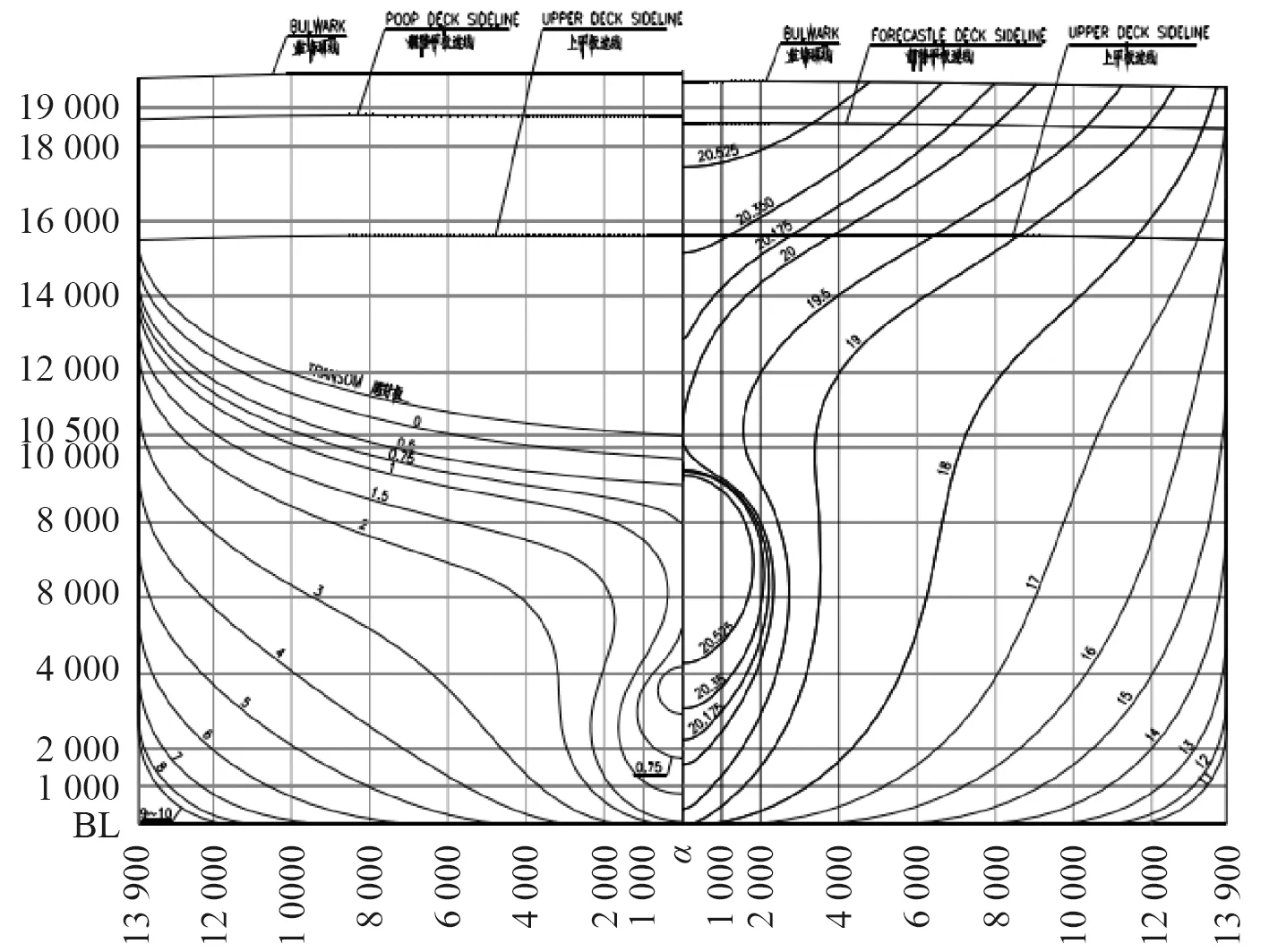
图4 船舶型线图[14]Fig.4 Hull lines

图5 试验船模[14]Fig.5 Test model of ship

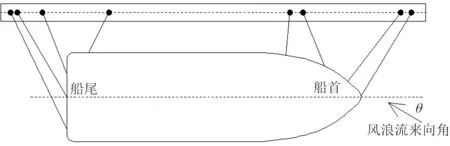
图6 系泊示意图Fig.6 Schematic diagram of mooring

3 试验验证及结果分析

3.1 程序可靠性验证

船舶水池系泊试验时，以波浪载荷试验对程序可靠性予以验证，试验在船舶满载、静风、静流工况下，分别验证了波浪入射角度 θ为5°，10°，15°，20°，25°，30°，波浪周期T为4.5 s，波高为0.3 m 时的波浪载荷Ff，对比结果如表2 和图7 所示。其中，Ffx0为波浪载荷横向分力试验值，Ffx1波浪载荷横向分力试验值；Ffy0为波浪载荷纵向分力试验值，Ffy1波浪载荷纵向分力试验值，kN。

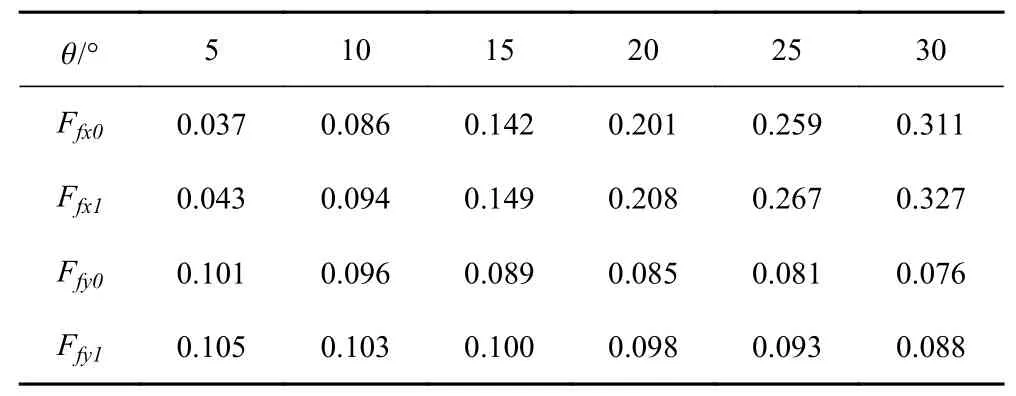
表2 波浪载荷对比结果Tab.2 Comparison results of wave load

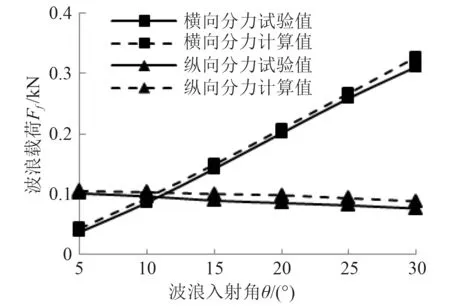
图7 波浪载荷试验与计算曲线Fig.7 Test and calculation curve of wave load

由图7 可以看出，程序计算结果与水池试验结果总体趋势一致，计算值总体是试验值1.0～1.1 倍，最大偏差0.013 kN，原因在于：为保证系泊安全，理论计算方法相对保守，其系数因子取值偏大；其次，从波浪载荷理论计算公式可以看出，横向分力曲线符合正弦变化，纵向分力曲线符合余弦变化，通过0°～180°波浪入射角度的波浪载荷程序计算，结果曲线满足上述规律，可验证该程序计算的有效性与可靠性。

3.2 浪、流特性分析

3.2.1 浪载荷特性

研究船舶满载、静风、静流工况下，浪向角θ分别为0°，15°，30°，45°，60°，75°，90°，波高H分别为0.1 m，0.15 m，0.2 m，0.25 m，0.3 m，0.35 m，0.4 m时的船舶浪载荷响应，对比结果如图8 所示。

由图8 可知：

1）在浪横向载荷曲线中，图8（a）随浪向角增加，曲率逐渐变小，曲线上升变缓，相邻曲线间距基本一致，符合试验结果趋势与精度；图8（b）随波高的增加呈线性增长，曲率基本保持一致，且随着角度的增加，同一波高下的相邻曲线间距逐渐减小；

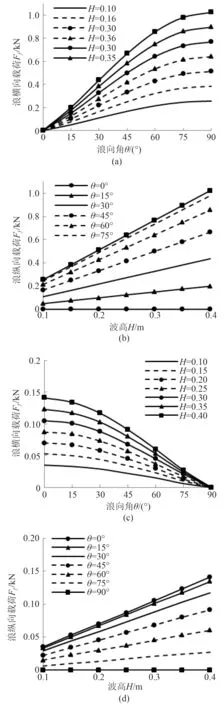
图8 浪载荷特性对比曲线Fig.8 Correlation curve of flow load

2）在浪纵向载荷曲线中，图8（c）随浪向角增加，曲率逐渐变大，图8（d）同样呈线性增长趋势，曲线特性与图8（b）相同。

3.2.2 流载荷特性

流载荷特性主要研究了静风、静浪，船舶满载工况下，流向角φ分别为0°，15°，30°，45°，60°，75°、90°，流速分别为0.1 m/s，0.2 m/s，0.3 m/s，0.4 m/s，0.5 m/s 时的船舶流载荷响应，对比结果如图9 所示。

由图9 可知：

1）在流横向载荷曲线中，图9（a）随着流向角的增加，曲率逐渐增大，曲线上升速率加快，相邻流向角曲线随流速的增加，间距逐渐成扩大趋势；图9（b）随着流向角的增加，曲率变小，曲线上升速率变缓，相比流向角，流速对流载荷影响更为明显；

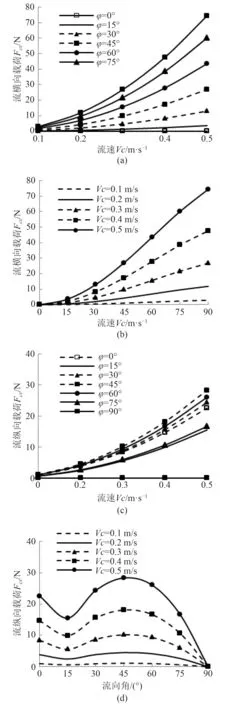
图9 流载荷特性对比曲线Fig.9 Correlation curve of wave load

2）在流纵向载荷曲线中，图9（c）呈现明显的聚类现象，不同于常规受力分析，流向角为45°时，船舶流纵向载荷最大，且流向角为0°时，流纵向载荷较低，图9（d）趋势同样反映出该现象，计算结果与试验结果及OCIMF 规范存在较大差异，其原因在于：国内《港口工程载荷规范》中流载荷系数计算只给出船舶方形系数为0.825 与0.625，水深吃水比为1.1 和1.5 工况下的系数计算方法，本文水深吃水比为11.76，超出规范量程，基于静态理论计算方法的局限性，导致程序静态计算时的误差偏大。

4 结语

本文首先基于国内《港口工程载荷规范》载荷计算方法，编程实现了船舶系泊过程中风、浪、流载荷的动态参数化计算，解决了人工计算繁琐、精度较低以及试验周期长、成本偏高等问题，通过试验验证了程序计算的可靠性，并进一步分析了系泊过程中浪、流载荷的变化特性，得出以下结论：

1）本文编程实现的船舶系泊过程中波浪载荷的动态参数化计算结果与试验结果拟合度可达90%，满足波浪载荷计算要求，具有一定的实用性；

2）国内《港口工程载荷规范》中流载荷计算结果与试验结果趋势偏差较大，实际工程的适用性不足，该理论计算尚需进一步完善；

3）本文分析了单一环境因素对系泊特性的影响，基于风浪流耦合作用于下的船舶系泊理论计算、数值模拟与试验研究仍需进一步研究。