加筋混凝土支护桩合理最大桩间距分析
2021-09-17徐永旺杨文超李裕忠魏伟琼
徐永旺,杨文超,李裕忠,魏伟琼
(中国电建集团贵阳勘测设计研究院有限公司, 贵州 贵阳 550081)
随着高层建筑、地铁、地下商业街、城区改造等地下空间的不断建设,基坑支护已经成为了不可或缺的施工步骤。基坑的施工难度也随基坑规模和深度的增加而逐渐增大。特别是在旧城区中,深基坑邻近旧建筑或古建筑,基坑开挖会对老旧建筑产生非常严重的后果,如下沉、开裂甚至倒塌等[1]。但是,目前支护桩桩间距的确定只能依据规范和相应的工程经验,没有合适简单的计算公式。因此,确定支护桩合适的桩间距既能减少资源的浪费降低工程成本,又能充分发挥支护桩的阻滑能力[2]。
关于支护桩桩间距的确定方法近些年也有许多学者进行了相应的研究,其中大多数学者研究的出发点都是基于桩间土体所形成的土拱效应(见图1),并从不同的强度理论、桩体模型、土拱迹线等方面入手推导出了相应的支护桩和抗滑桩桩间距的计算方法。概括起来大概有五类:第一类是以王成华等[3]、李长冬等[4]为代表,根据“桩间滑动土体的推力不大于桩间土体与抗滑桩桩两侧的摩阻力之和”为理论依据,推出了桩间距的计算公式;第二类是以蒋良潍等[5]、赵明华等[6]、王培勇等[7]、陈龙等[8]为代表,将桩间土体形成的土拱作为研究对象,建立几何模型并对该模型建立对称的抛物线方程,根据Mohr-Coulomb强度破坏准则为控制条件确定桩间距并推出了相应的计算公式;第三类则是以胡敏云等[9]为代表,根据大小主应力理论为依据,推出了相应的桩间距计算公式;第四类是以周德培等[10]、刘涛等[11]、张玲等[12]、杨帆等[13]为代表,根据土体静力平衡条件及Mohr-Coulomb强度破坏准则为理论依据,推出了桩间距的计算公式;第五类是以陈秋南等[14]为代表,从双剪强度理论三维角度出发并考虑了第二主应力对土体的破坏,推出了相应的桩间距计算公式。
上述的五类理论大都是以桩间土体产生的土拱效应为研究对象,建立几何方程,采用不同的强度准则,得到支护桩最大桩间距的计算公式。由于选用的几何方程、强度准则及不同公式省略的影响因素均不相同,所以得到的最大桩间距计算结果差别较大[15],且计算公式过于复杂,并不适合工程技术人员的应用。马显春等[16]提出,上述所提及的五种桩间距计算公式都与桩间土体的黏聚力和内摩擦角有关系,但是考虑在无黏性土的施工场地计算时,黏聚力的取值应该为零,则利用上述五种计算方法得到的桩间距也为零,这明显与实际施工情况不符。
目前基坑支护桩桩间距的确定主要依据《建筑基坑支护技术规程》[17](JGJ 120—2012),对悬臂式排桩、支护桩的桩径宜大于或等于600 mm;排桩中心距不宜大于桩直径的2.0倍。而在地质灾害防治中,抗滑桩桩间距的确定则根据《地质灾害防治工程设计规范》[18](DB 5029—2004),抗滑桩的间距一般为桩径的3.0~5.0倍。由此可以看出不同行业和地区对最大桩间距的规定差别较大。
结合上述原因在对支护桩桩间距确定的问题上并没有得到较好的方案与公式,本文从工程实际出发,结合施工场地的地质情况拟寻求一种简单合理的支护桩最大桩间距的计算公式。
1 支护桩的最大桩间距计算
马显春等[16]在利用抗滑桩斜截面受剪承载力计算其最大抗滑承载力的基础上,根据极限状态下单根桩的最大抗滑承载力恰好等于桩间距范围内滑坡土体的剩余下滑力为理论依据,推出了抗滑桩的最大桩间距的计算公式,计算结果准确可靠。在此理论基础之上本文提出:以圆形支护桩为研究对象,在利用支护桩斜截面受剪承载力计算其最大水平承载力的基础上,根据极限状态下单根支护桩的最大水平承载力恰好等于桩间距范围内所夹土体的总主动土压力,推导出基于支护桩斜截面受剪承载力的最大桩间距计算公式。
1.1 桩后土压力计算
目前朗肯土压力理论是计算桩后土压力大小最常用的土压力理论,其概念明确,方法简单。朗肯土压力理论有两个基本假设:(1) 挡土墙墙背竖直且光滑;(2) 挡土墙墙后土体表面水平且无限延伸(见图2)。认为墙后各点土体均处于极限平衡状态,应用极限平衡条件,推导出了主动土压力和被动土压力的计算公式。

图2 挡土墙后土体表面情况
在进行基坑开挖与支护时,支护桩桩后土体的破坏类型可视为主动破坏状态。根据朗肯主动土压力理论,作用于任意z深度处土单元上的竖向应力σz应是最大主应力σ1,而作用在墙背的水平土压力ea应是最小主应力σ3,即:
σz=σ1,ea=σ3
(1)
式中:σz为单元体竖向应力,kPa;σ1为单元体最大主应力,kPa;ea为主动土压力强度,kPa;σ3为单元体最小主应力,kPa。
当土单元体处于极限平衡状态时所受的大、小主应力应满足式(2):
(2)
式中:φ为土的内摩擦角,(°);c为土的黏聚力,kPa。
因此,任意z深度处土体所产生的朗肯主动土压力的计算公式可以表示为:
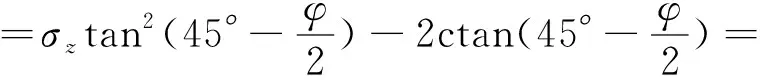
(3)
(4)
式中:Ka为朗肯主动土压力系数。
当基坑上部土体有均布荷载作用的情况下,桩间距范围内所夹土体的总主动土压力由三部分组成:(1) 由基坑上部均布荷载所引起的土压力,该部分土压力大小与深度无关,土压力沿桩高呈矩形分布;(2) 由土体自重引起的土压力,该部分土压力与深度成正比,土压力沿桩高呈三角形分布(见图3);(3) 由黏聚力c产生的抗力,表现为负的土压力,起减少土压力的作用,其值为常量,不随深度变化。

图3 均布荷载作用下的黏性土主动土压力分布
得出桩间距范围内所夹土体的总主动土压力Ea的计算公式,即:
(5)
式中:Ea为总的主动土压力,kN/m;γ为土的重度,kN/m2;H为支护桩长度,m。
由式(1)—式(5)可以看出在实际工程中根据朗肯主动土压力理论,能够方便快捷地计算出桩间距范围内所夹土体的总主动土压力。
1.2 最大水平承载力计算
基坑支护桩属受弯构件,其弯矩与桩后土压力、桩前侧土体抗力及配筋等因素有关,其水平承载力用弯矩来确定相对较复杂,因此,本文利用支护桩斜截面的受剪承载力来确定其水平承载力。
基坑支护中的桩截面通常为圆形,根据《建筑基坑支护技术规程》[17](JGJ 120—2012)以及《混凝土结构设计规范》[19](GB 50010—2010)的规定,圆形截面受弯构件的受剪截面的最大剪力设计值应符合下列规定:
Q≤0.704βcfcr2
(6)
式中:Q为构件斜截面上的最大剪力设计值,N;βc为混凝土强度影响系数:当混凝土强度等级不超过C50时,βc取1.0;fc为混凝土轴心抗压强度设计值,N/mm2,取值见表1;r为圆形截面混凝土桩的半径,mm。
根据桩间距范围内所夹土体的总主动土压力和土体性质确定支护桩类型、尺寸及配筋,并计算出该支护桩所受最大剪应力及其部位,在最大剪应力值满足式(6)式时,可以根据以下方法计算支护桩斜截面的受剪承载力。
在工程中,圆形支护桩往往配置有箍筋与加强筋,而对于仅配置箍筋的圆形截面受弯构件,其截面受剪承载力的计算需满足下列规定:
(7)
式中:ft为混凝土轴心抗压强度设计值,N/mm2,取值见表1;fyv为箍筋的抗拉强度设计值,N/mm2,箍筋常用的牌号抗拉强度设计值: HPB300为270 N/mm2,HRB335为300 N/mm2,HRB400、HRBF400、RRB400为360 N/mm2;Asv为配置在同一截面内箍筋各肢的全部截面面积,mm2;s为沿构件长度方向箍筋间距,mm。

表1 混凝土轴心抗压、抗拉强度设计值
(8)
式(8)即为圆形截面支护桩最大水平承载力。
1.3 最大桩间距计算
通过式(8)确定的圆形截面支护桩最大水平承载力,结合桩间距范围内所夹土体的总主动土压力,可以得出支护桩的最大桩间距,即:
(9)
式中:S为支护桩中至中的最大桩间距,m。
将公式(5)和式(8)带入式(9),可得:
(10)
通过上述分析可得出,圆形支护桩的截面尺寸确定后,其斜截面的受剪承载力为定值,最大桩间距与桩间距范围内所夹土体的总主动土压力成反比,总主动土压力越小,桩间距越大,反之亦成立。
2 工程实例计算
利用文献[14]中提供的工程实例来验算本文所提出方法的合理性。株洲市某高层建筑物基坑开挖,所选用的支护形式为桩锚支护,桩径d=1 m,支护桩桩长H=13 m,桩身嵌固深度h0=3 m。场地土质以黏性土为主,根据地质勘察报告,桩后土体的黏聚力c0=40 kPa,内摩擦角取φ0=20°,地面均布荷载q0=10 kN/m2,土体的重度近似取γ0=20 kN/m2[9]。
通过采用朗肯土压力理论计算桩间距范围内所夹土体的总主动土压力。考虑工程的安全性预留一定的安全系数,所以在计算桩间距范围内所夹土体的总主动土压力时不考虑由黏聚力c产生的抗力,即不考虑拉应力区。可得:
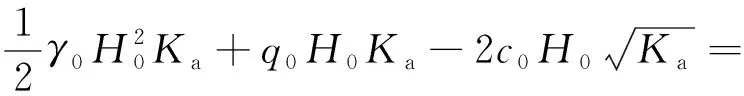
495.9 kN/m
桩间距范围内所夹土体的总主动土压力值为495.9 kN/m。
基坑支护桩桩体的配筋方案参考《混凝土结构设计规范》[19](GB 50010—2010),采用桩径1 000 mm,混凝土强度C30,主筋使用HRB400的钢材,14φ20;加强筋使用HRB400的钢材,16@2000;螺旋箍筋使用HBR335钢材,箍筋配筋8@200的配筋方式。
考虑到圆形截面支护桩加强筋的作用,沿构件长度方向的箍筋间距作减半处理,将上述数值代入式(8)计算,即:
将Q、Ea的值代入式(9)可得:
可得出基坑支护桩最大桩间距为1.91 m。
在计算桩间距范围内所夹土体的总主动土压力时已将黏聚力c产生的拉应力区给忽略,为工程留出了较大的安全保障。考虑实际情况及工程成本时可采用折减系数法n对最大桩间距进行调整,即:
(11)
(12)
式中:z0为拉应力区深度,m。
计算得:
将本文计算结果与文献[14]中的双剪理论、绕流理论和规范法桩间距计算结果进行比较(见表2)。
通过表2可得出,本文的计算结果与双剪理论法和绕流理论法所得的结果相差不大,误差在7%~11%之间。与规范法相比,本文比绕流理论法得到的结果偏于安全,更接近国家基坑支护规范的计算结果,且<2d(支护桩桩径)。在此基础上采用折减法所得到的结果有一定的合理性,对工程成本的控制有一定的参考意义。
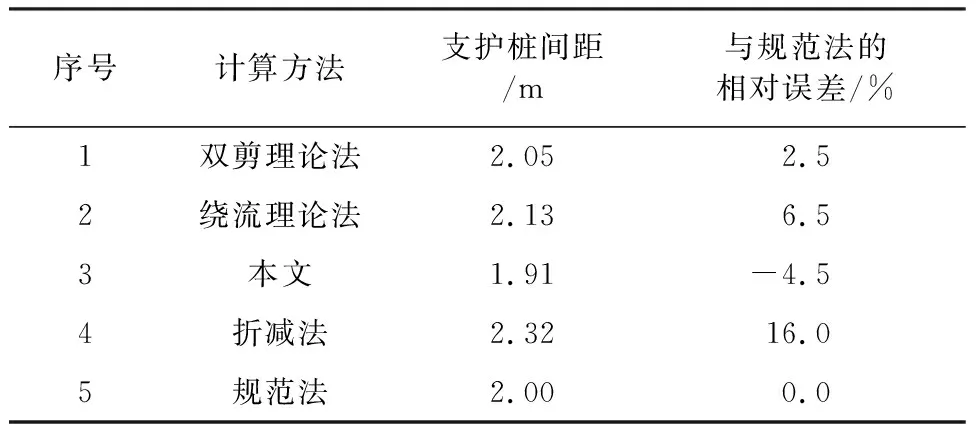
表2 5种方法的计算结果比较
3 实例延伸分析
在上述工程的基础上,根据式(9)和式(10)且考虑支护桩加强筋的影响,在工程地质条件不变的情况下Ea不发生变化,将Ea视为常数A,则式(10)可化为:
(13)
式中:A为确定工程桩间距范围内所夹土体的总主动土压力值,为常数,kN/m。
可得出当桩间配筋情况相同时,最大桩间距S是关于桩径r的一元二次方程;当桩径r确定时,最大桩间距S与桩身混凝土抗拉强度、箍筋抗拉强度、箍筋半径及箍筋间距均有一定的关联。采用控制变量法分析各因素对最大桩间距的影响,见图4—图8。

图4 桩身混凝土抗拉强度设计值改变对最大桩间距的影响
以上述工程采用的数据为标准:ft=1.43 N/mm2;fyv=300 N/mm2;Asv=100.53 mm2;s=200 mm。
通过图4—图8可得出支护桩的桩身直径对最大桩间距的影响最为明显,其次是箍筋半径,螺旋箍筋抗拉强度设计值和桩身混凝土抗拉强度设计值对

图5 螺旋箍筋抗拉强度设计值改变对最大桩间距的影响

图6 同一截面内螺旋箍筋半径改变对最大桩间距的影响
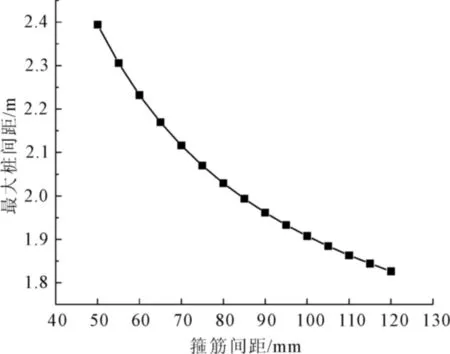
图7 螺旋箍筋间距改变对最大桩间距的影响
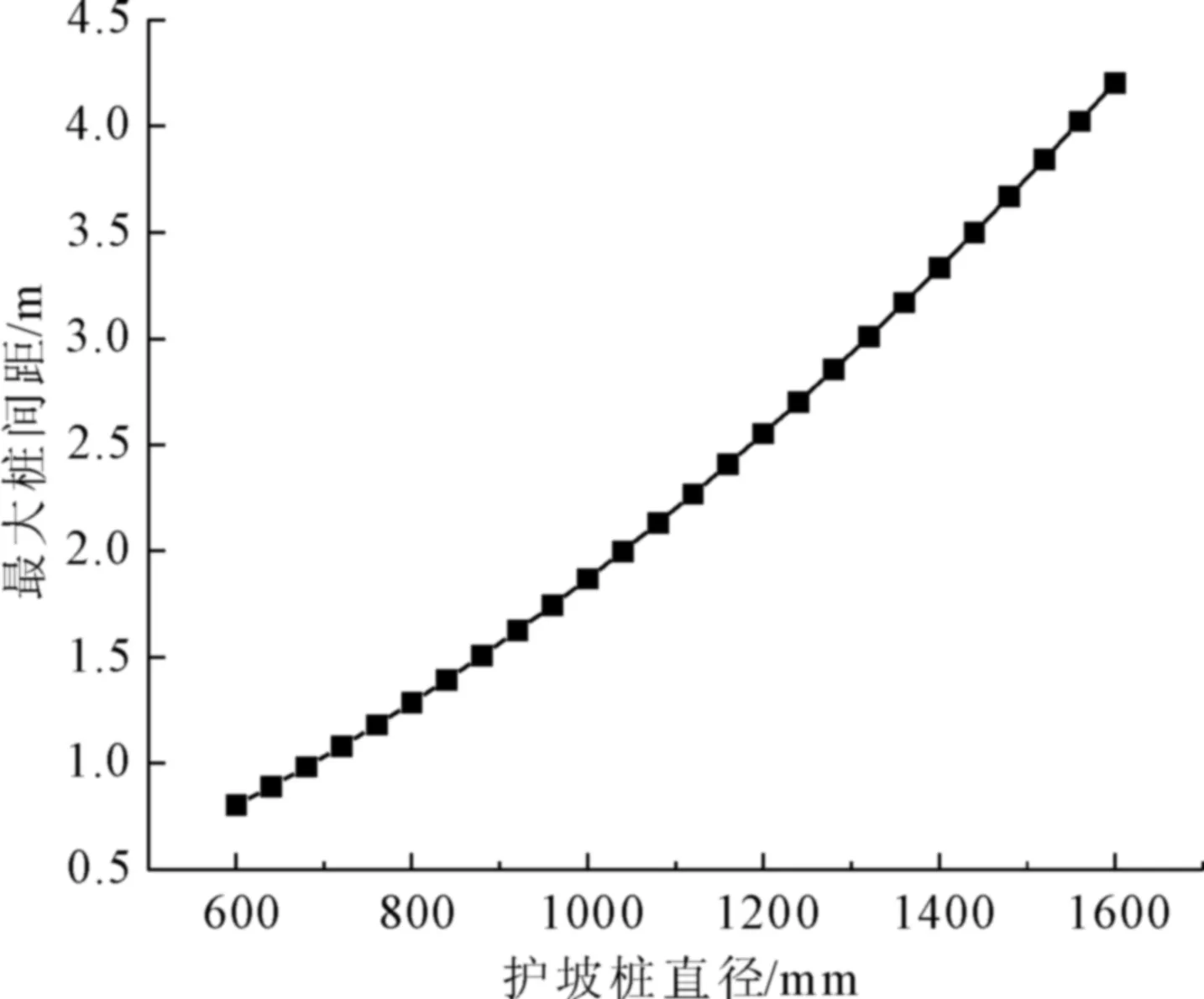
图8 支护桩桩身直径改变对最大桩间距的影响
最大桩间距影响较小,螺旋箍筋间距与最大桩间距呈反比例关系。在进行深基坑支护桩支护设计时,若桩间距范围内所夹土体的总主动土压力一定时,可适当减少箍筋的抗拉强度和箍筋间距来增大桩间距;或在桩身斜截面受剪承载力设计满足安全的前提下适当增加支护桩的桩身直径来增大桩间距。得到适合于工程的最大桩间距,进而节省工程成本,提高工程施工效率。
4 结 论
(1) 本文以深基坑支护中的圆形截面支护桩为研究对象,利用桩身的斜截面受剪承载力在极限状态下恰好等于桩间距范围内所夹土体的总主动土压力,推导出了简单、实用和便于理解计算的圆形截面支护桩合理最大桩间距的计算公式。
(2) 利用工程实例,与基于双剪理论和绕流理论及规范法桩间距计算结果进行比较,结果相近,验证了本方法的合理性,与前两者相比,本文的支护桩最大桩间距计算公式更简单实用,适合在实际工程中推广应用。
(3) 在工程实例基础之上采用控制变量法分析得出支护桩的桩径对桩间距的影响最为明显,其次是箍筋半径,螺旋箍筋抗拉强度设计值和桩身混凝土抗拉强度设计值对支护桩的最大桩间距影响较小,螺旋箍筋间距与最大桩间距呈反比例关系。提出了适当增加支护桩的桩身直径或增加箍筋配筋率得到适合工程的最大桩间距。有效的避免了桩间距过小造成工程成本的上升,桩间距过大造成桩间土失稳。
