基于滚动阻力模型的加筋碎石三轴试验数值模拟研究

2021-09-17商昆麒樊赟赟

水利与建筑工程学报 2021年4期

商昆麒，樊赟赟

(东北大学资源与土木工程学院，辽宁沈阳 110004)

岩土体与土工合成材料的界面性能决定着加筋结构的稳定性和有效性，一直是加筋技术领域的研究热点之一。当前用于测定加筋岩土体特性的试验方法包括直剪试验、拉拔试验和三轴试验三类。其中三轴试验是最为重要的手段之一。学者们利用三轴试验研究土工合成材料加固岩土体的作用机理，提出了诸如“等效围压”和“准黏聚力”等力学原理[1]。王家全等[2]为探究循环动载作用下加筋砾石土的动力特性，在不同加筋层数和围压下对加筋砾石进行了固结不排水动三轴试验，研究加筋层数和围压对加筋砾石动力特性的影响。Prabhu等[3]通过三轴试验，对土工格栅加筋、土工格室加筋和无加筋地基在反复荷载作用下的弹性模量进行了评价和比较，对地基的加固效果形成了新的认识。刘方成等[4]基于三轴试验，对三种不同格栅布置方式下的干燥橡胶砂强度特性展开研究，重点考察加筋层数对不同围压和配比下橡胶砂的峰值强度、黏聚力、内摩擦角的影响规律。试验手段成为加筋岩土体宏观力学性能研究的基础。

常规的试验手段能够得到加筋岩土体的宏观力学参数，但在进一步研究细观力学机理和规律时则受到一定限制。随着现代计算技术的不断进步，数值模拟技术得到了长足发展，其中用于模拟散体细观力学性质的离散元法成为研究加筋土的一项重要手段。董博文等[5]针对目前土石坝工程中最常采用的双向塑料焊接土工格栅和双向涤纶经编土工格栅,采用大型拉拔试验设备完成了两种格栅在堆石料中的拉拔试验,以研究其与堆石料的相互作用机制及加筋效果。苗晨曦等[6]为分析网孔形状对格栅加筋性能的影响，采用离散元对土工格栅拉拔过程进行了分析，揭示了剪切带形成演化和剪切带内颗粒接触力的细观组构特征，并比较了不同网孔形式的加筋性能。Chen等[7]建立了两种形态的平行键土工格栅离散元模型用于拉拔试验模拟，并用理想形状颗粒模型进行了验证。郜家奇等[8]结合离散元方法采用clump-ball混合的落雨式分层过压建模法构造了大三轴数值模型。结果表明,构造方法更接近实验室制样过程,数值模型满足室内试验级配和孔隙率要求,为研究颗粒形状对堆石料力学特性影响作铺垫。

在传统理想球体离散单元中，没有考虑颗粒之间的滚动的影响，模拟中颗粒被设定自由滚动，或者完全限制其滚动，对颗粒滚动阻力的考虑不足。Oda等[9]通过试验发现决定颗粒材料细观变形机制的主要因素不仅是颗粒间滑动，还包括颗粒间的滚动。Smith等[10]对滚动摩擦的成因进行了研究，认为土体变形使受力变得不均匀而产生滚动阻力。因而，对具有不规则性的现实颗粒除可以采用复杂形态离散单元或颗粒簇单元模拟外，还可以通过引入滚动阻力模型考虑颗粒形态不规则形的影响。Iwashita等[11]在接触模型中加入滚动分量，分析了滚动对数值模拟结果的影响。Belheine等[12]建立了考虑颗粒滚动阻力的三维接触模型用来模拟实际材料，数值模拟结果与实验结果吻合较好。Ai等[13]在对比分析几种阻力模型的基础上提出了一个较为通用的滚动阻力模型。滚动阻力模型丰富了离散元理论，拓展了离散元的应用空间。Zhou等[14]通过研究认为滚动阻力能在一定程度上决定着颗粒形状对峰值抗剪强度的影响，但在颗粒较小时这种影响并不明显。

综合已有文献可知，一般在岩土体颗粒受到约束而滚动受限的情况下，应用滚动阻力模型的离散元方法有望得到良好的模拟效果。本文尝试采用滚动阻力模型对三轴加筋碎石试验进行离散元模拟，研究各细观参数的标定方法及其对数值试验曲线的影响。

1 滚动阻力模型

滚动阻力模型是在线性模型的基础上发展建立起来的一个接触模型。滚动摩擦力对颗粒的平动与滚动均具有减速作用。

在滚动阻力线性模型中力与位移关系中的接触力和力矩设定为：

Fc=Fl+Fd，Mc=Mr

(1)

式中：Fl为线性接触力；Fd为阻尼力；Mr为滚动阻力矩。

Fl和Fd的设定方法与线性接触模型相同，可表示为：

Fl=knδnij+ktδtij

(2)

Fd=-γnvnij-γtvtij

(3)

式中：kn，kt分别为法向、切向接触刚度；δnij、δtij分别为法向、切向重叠量；γn、γt分别为法向、切向相对速度。颗粒间发生滑移的条件是Ft>μFn(Fn和Ft分别为法向和切向力，而μ则为颗粒间的滑移摩擦系数)。

滚动阻力矩的增量可由式(4)更新为：

(4)

式中：Δθb是相邻颗粒间的相对转角。而kr为滚动阻力刚度，为滚动阻力矩增量与接触点相对滚动增量相关的常数，可用剪切刚度与有效半径表示为：

(5)

(6)

式中R(1)和R(2)分别是两接触单元的半径。

依据限定极限扭矩阈值检查滚动阻力矩的大小：

(7)

式(7)中极限扭矩等于当前法向力与滚动阻力系数和有效半径的乘积，可表示为：

(8)

式中：μr为滚动摩擦系数。

滚动阻力矩的模型如图1所示。

图1 滚动阻力矩计算模型

在滚动阻力线性接触模型中，主要通过变化滚动摩擦系数μr实现对颗粒滚动的限制。

2 数值模型建立

文献[15]分别对加筋和未加筋条件下的碎石试样进行了三轴加载试验，由碎石制作的试样尺寸为310 mm×610 mm(直径×高)，为充分模拟碎石在列车运行条件下的高速加载，试验在138 kPa的围压下以每秒5%的速率施加了快速的轴向应变以测试碎石的抗剪性能。试验采用了具有级配的石灰石，碎石材料的级配组成如图2所示，其颗粒的不均匀系数Cu=1.46，曲率系数Cc=0.97，孔隙比为0.68，质量为70 kg。试验所用的石灰石碎石和格栅如图3所示。

图2 石灰石碎石的颗粒级配曲线

图3 试验用碎石和土工格栅[15]

结合试验的实际情况，根据试样的尺寸利用圆柱和平面wall单元建立起加载的边界条件，然后利用无黏结接触的ball单元建立起与石灰石碎石级配相同的颗粒模型，最后采用刚性颗粒簇单元模拟土工格栅，所建立土工格栅模型与实际格栅在网孔形态与尺寸等方面保持一致。在试验中利用伺服机控制围压使之与试验的围压保持一致，并以试验的加载速率移动上下两块加载平板以模拟三轴加载试验的过程。依据文献[15]试验所建立起来的三轴加载数值模型如图4所示。

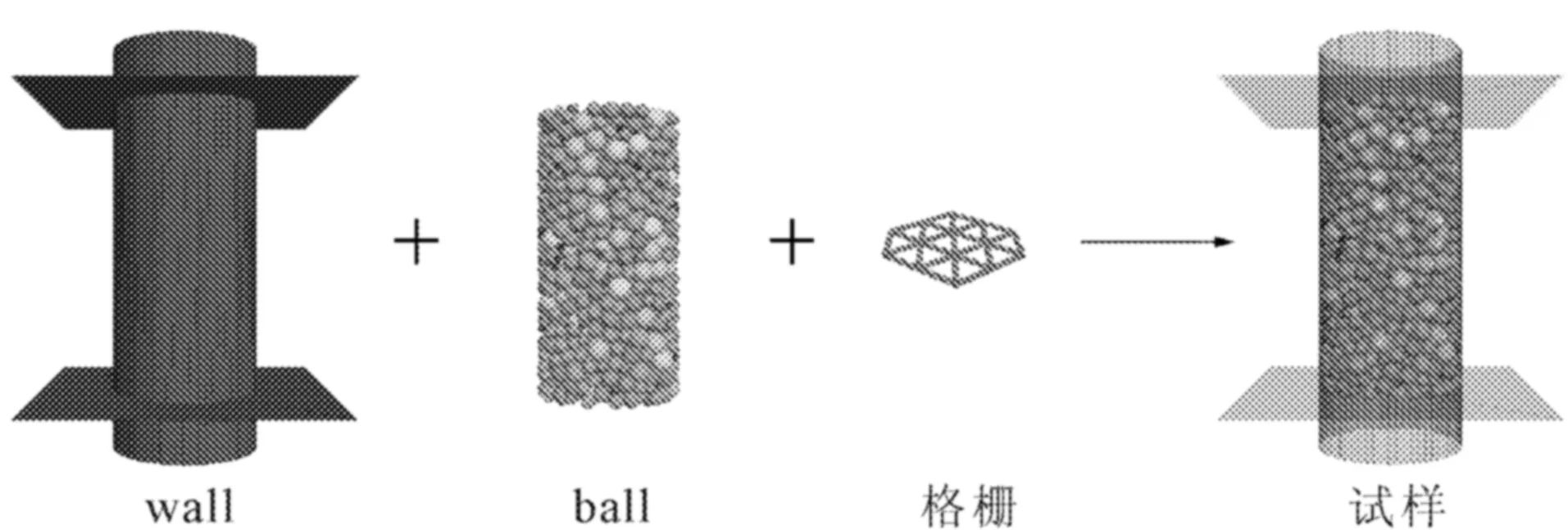
图4 三轴加载试验的数值模型

细观参数的合理确定是利用离散元有效实现三轴试验数值模拟的关键。根据文献的宏观密度和所建立起模型的实际体积，可利用质量相等的原则根据关系式(9)计算求得：

(9)

式中：ρb为球体的密度；vi为球体的体积；ρ为碎石试件的密度；r和h则分别为试样的半径和高度。

根据式(9)可以确定出球体的密度为2 625 kg/m3，这基本与石灰石的密度相一致。同时根据文献所给数据可以确定出滑移的摩擦系数。而离散元计算所采用的其他细观参数则需要进一步利用数值试验的方法加以校准与确定。

3 数值试验与分析

除密度(2 625 kg/m3)和滑移摩擦系数(0.6)可根据文献确定外，在本次数值试验中碎石的其他细观参数与宏观参数间并没有确定的关系，但仍有一些规律可以借鉴[16-18]。对于碎石三轴试验而言，需要进一步确定的参数主要是与弹性模量密切相关的离散单元接触刚度，其中为避免计算中颗粒单元穿透墙体单元，墙体单元的刚度一般设置的比颗粒单元要更大一些[16-18]。基于线性滑移接触模型的数值三轴试验可以得到在不同接触刚度下的宏观弹性模量，如图5所示。

由图5可见，尽管离散单元的接触刚度几乎不会对(σ1-σ3)-ε1曲线的峰值强度产生影响，但其却能对弹性模量产生主要的影响，这种影响主要体现在所得(σ1-σ3)-ε1曲线的初始斜率上。从初步的数值试验基本可以确定接触刚度大致范围，通过进一步细化的数值试验得到如表1所示的计算结果。

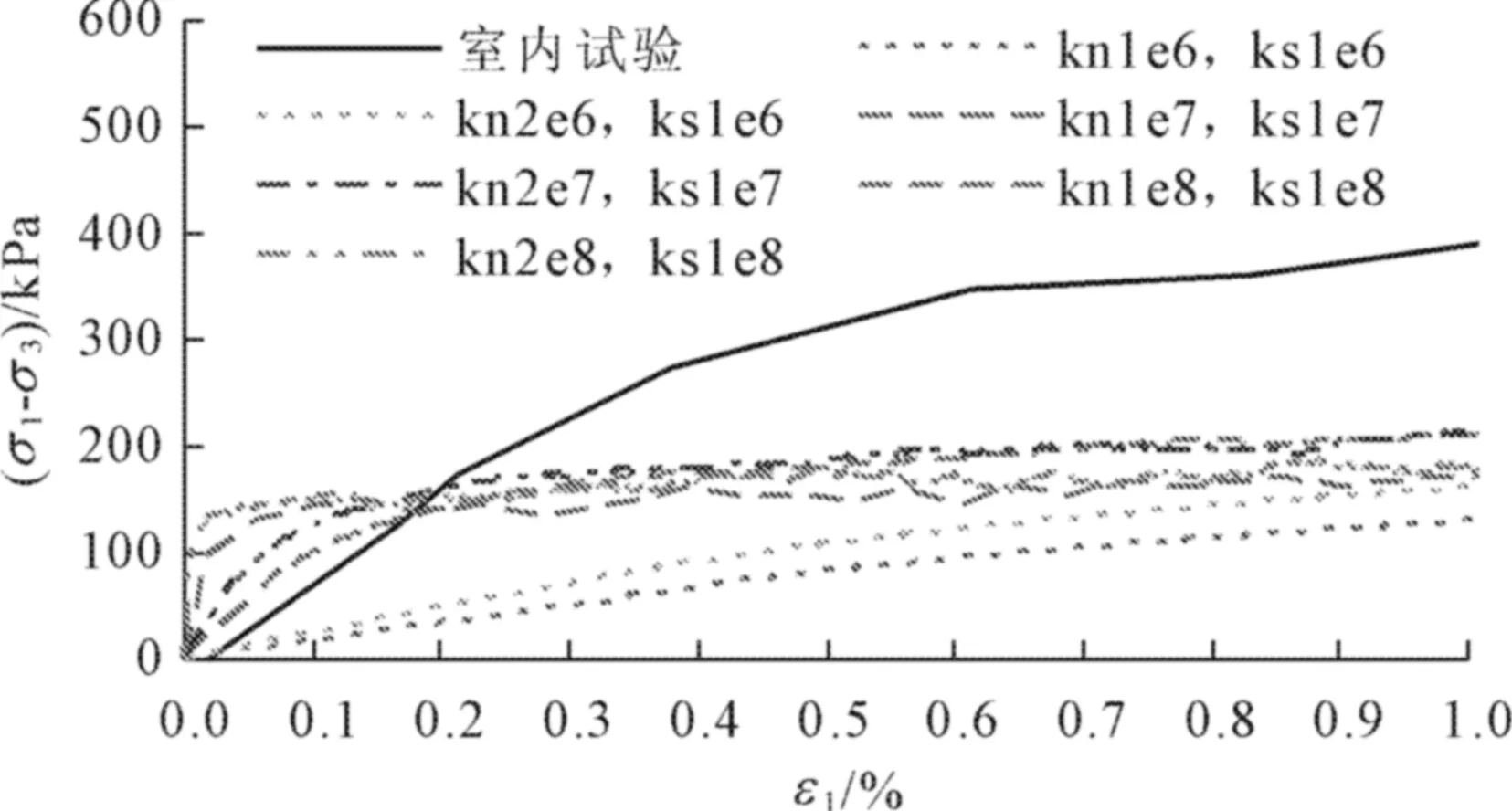
图5 不同接触刚度条件下数值试验与试验数据的对比

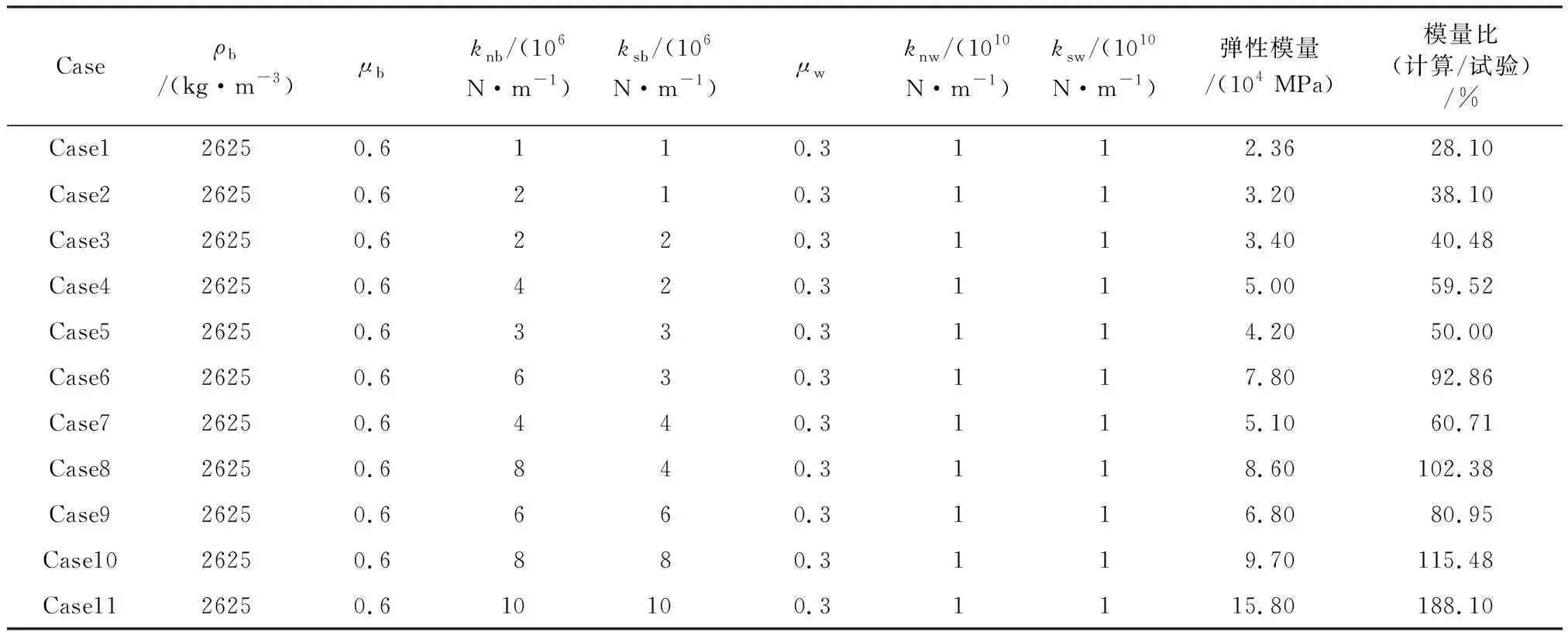
表1 弹性模量的计算与校准

从表1所示的计算与试验的模量比可见，在Case8条件下数值模拟所得到的弹性模量基本与试验的数值相符，从而完成了对离散单元接触刚度的校核。然而，尽管校准后的接触刚度会使数值模拟的曲线在初始阶段与试验数据吻合良好，但接触刚度不能对强度峰值产生更大的影响，因而所得到由理想球形单元和线性滑移接触模型的模拟曲线峰值与试验却相差甚远。

采用基于复杂形态的离散单元或者颗粒簇单元的方法可以考虑颗粒形态对(σ1-σ3)-ε1曲线的影响，但要为接触搜索和单元存储付出较大的计算代价。采用球形单元的滚动阻力模型能够考虑由颗粒形态产生的滚动阻力影响，有望在低计算成本条件下实现对碎石三轴试验的有效模拟。将滚动阻力模型应用到计算模型中，通过调整滚动阻力系数可以体现由不规则形状产生的颗粒间的咬合摩擦作用。在表1所示Case8参数的基础上增加不同的滚动阻力系数，得到了不同滚动阻力系数条件下的碎石的三轴数值试验曲线，如图6所示。

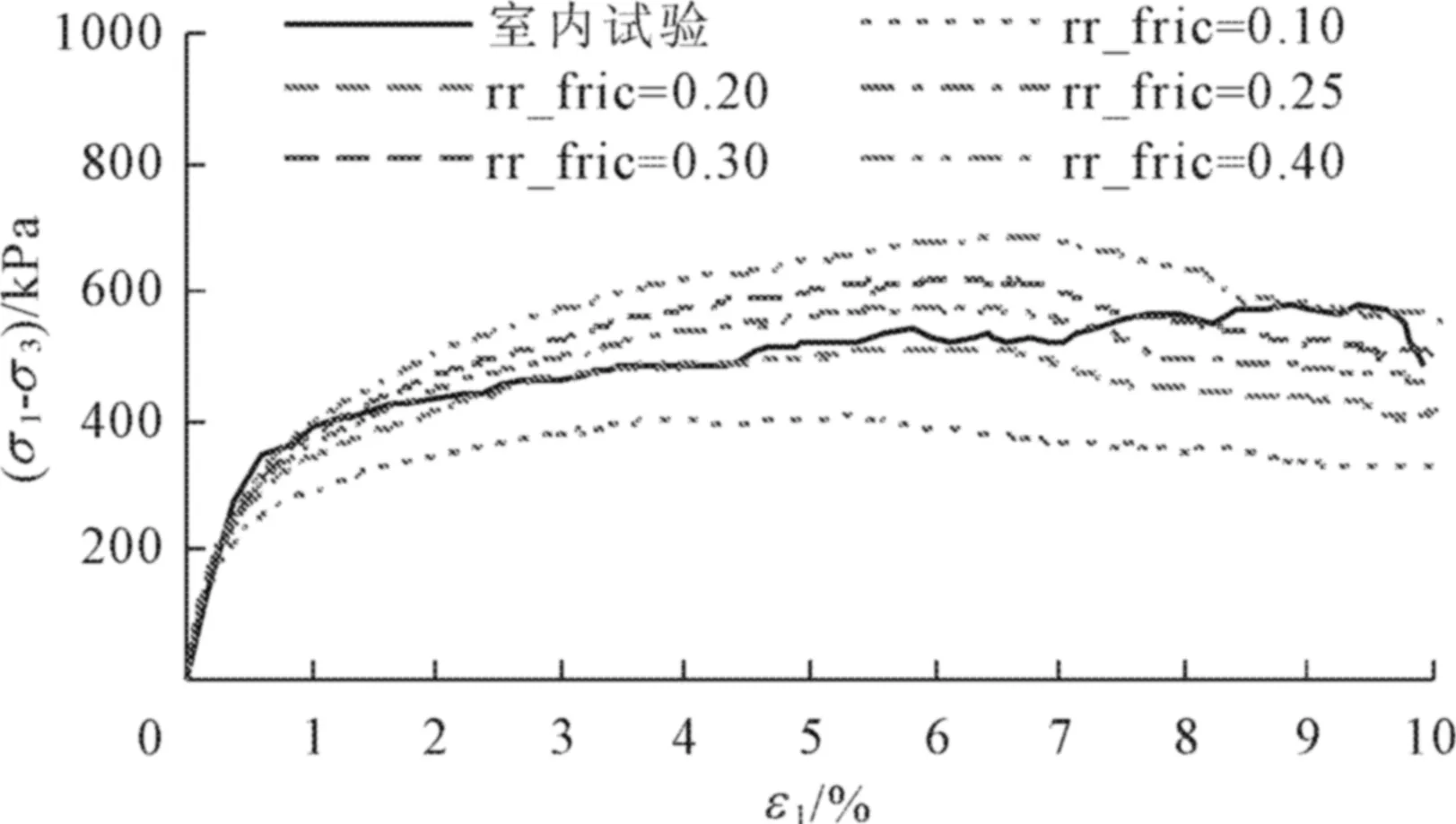
图6 碎石三轴数值试验模拟曲线与试验数据对比图

从图6可见，随着滚动阻力系数μr的增加，(σ1-σ3)-ε1曲线的峰值也随之逐渐增加。从数值试验结果来看试验曲线基本处于μr=0.2和μr=0.3的数值曲线之间，当μr=0.25时数值试验曲线与试验数据曲线的吻合最为良好，这说明对于文献[15]中的碎石材料和加载条件而言，采用滚动阻力模型能够实现对试验过程的有效的模拟。尽管数值模拟和试验的曲线已经足够接近，但我们仍然能够看到在曲线的后半段两者出现了一定的差异，数值曲线的下降段相对试验有所提前，这可能是由于在加载后期随着试样变形的增加，碎石间的咬合变得更加紧密，由颗粒形状所形成滚动阻力有所增加，从而所对应的滚动阻力系数也有所增加，但在缺少更具体根据的情况下本文的计算中并未对滚动阻力系数进行动态的调整。

采用刚性颗粒簇模型来对土工格栅进行模拟。在碎石三轴数值试验模拟的基础上加入土工格栅模型进行计算。参考相关的文献[15,19-20]，所采用的土工格栅细观计算参数如表2所示。

表2 土工格栅细观计算参数

加入土工格栅是提高碎石体宏观强度的一项重要举措，由于在力学机制上主要是通过对碎石体变形的限制以增强其整体性和增加碎石间彼此的咬合与摩擦作用。因而从力学机制和原理上，同样可以应用滚动阻力模型对加筋碎石进行数值模拟。在土工格栅的约束作用下，碎石间的滚动阻力增加，因而在模型中的滚动阻力系数也应有所增加。在碎石三轴数值试验的基础上，改变碎石的滚动阻力系数得到了如图7所显示的(σ1-σ3)-ε1数值试验曲线。

图7 加筋碎石三轴数值试验模拟曲线与试验数据对比图

从图7所示结果可见，当滚动阻力系数达到0.55时，数值模拟的曲线与试验数据曲线的吻合十分良好，从而也说明了滚动阻力模型能够很好的实现对加筋碎石三轴试验的有效模拟。在加入土工格栅的条件下，由于碎石所受到的变形限制增强，碎石间咬合摩擦的态势变化不大，因而即使采用不变的滚动阻力系数对整条试验曲线的模拟都能够与试验数据吻合的十分良好。

为对数值模拟效果进行对比，将几种数值处理方法的计算结果进行比较，如图8所示。其中多面体-线性接触曲线为参考文献[15]的数值结果，球体-滚动阻力曲线为本文采用滚动阻力模型所得到的数值结果，而球体-滑动阻力曲线为本文采用滑动阻力模型所得到的数值结果。

图8 不同数值模型的计算结果比较

从图8可见，采用复杂多面体形态离散单元对碎石三轴试验进行数值计算[15]，可以得到良好的模拟效果，但这需要付出更多的计算成本来完成接触关系的搜索判定及单元的存储，同时为使所建立模型与实际碎石形态等效，在碎石形态的随机数值建模中也可能会面临一些新的问题和困难。而滚动阻力模型可以考虑在滚动趋势下由复杂形态颗粒间咬合摩擦所产生的滚动阻力，这种阻力是由不规则形态所产生不均匀的颗粒间接触力而造成的。应用滚动阻力模型对加筋碎石三轴试验进行数值模拟，所得数值曲线与试验曲线的趋势基本一致且峰值较为接近，同样得到了较好的模拟效果。这是由于土工格栅对碎石约束使得颗粒间的咬合状态较为紧密，使得滚动阻力系数在加载过程中变化不大，因而滚动阻力模型适合于对变形约束更强的加筋碎石三轴试验的数值模拟。在本文的算例中试验碎石的滑移摩擦系数是确定的，若仅采用理想球体单元和线性滑移模型而不考虑由不规则形态造成的滚动阻力，则不能准确反映出三轴试验的应力应变关系，数值计算模拟的结果会与实际情况有很大的差别。