管桩处理软基对既有铁路影响研究

庞 拓

（中铁十六局集团路桥工程有限公司 北京 101500）

1 引言

由于铁路发展以及征拆困难，很多时候需要在既有铁路线附近新建铁路。由于新旧路基距离近，如何减小施工对既有铁路的影响就变得十分关键［1］。软土地基在我国十分常见，其具有孔隙率高、含水量高以及受力后变形大的特点［2］。当遇到这类地基时就必须对其进行加固处理，而在加固施工过程中稍有不当就会对既有路基产生较大影响，从而影响既有线路的正常通行［3］。

目前常用的软基处理方式包含堆载预压法、置换法、水泥搅拌桩法、预应力管桩处理法［4］。这几种方法各有优势，但是当上部填方高度较高时（一般大于4 m），预应力管桩处理方法具有十分明显的优势［5］。预应力管桩目前已经实现工厂化预制，具有制造效率高、制造工艺精湛、桩身强度大、外观尺寸精度高的特点，桩身竖向承载能力高、抗弯性能优良。因此，在铁路工程软基处理中运用十分广泛［6］。预应力管桩在处理软基过程中是通过在特定位置将预制管桩通过静压或者捶打的方式压入路基中，一方面通过管桩挤入将软土挤密，从而提高其承载能力；另一方面管桩本身也能承受上部荷载［7－8］。正是由于管桩处理软基时需要对原有土层进行挤压，这样势必会影响既有线路的路基，一旦影响过大就会威胁到既有线路的交通。而目前针对此类的研究大多还停留在施工经验上，对于理论研究鲜有报道［9－10］。

本文依托广梅汕铁路新增二线工程，针对预应力管桩在软基加固处理中的挤压作用对既有线路的影响开展理论研究［11－12］，以期指导设计和施工。

2 工程概况

广梅汕铁路增二线项目位于韩江三角洲滨海平原地区，地势开阔、地形平坦，相对高差0～2 m。该区域为韩江携带泥砂在其下游沉积而成，第四系沉积层厚度一般30～120 m，沉积厚度最大达168.4 m；上覆第四系人工填土1～3 m，淤泥质黏土厚度为15～32 m。既有线路路基多为填方地段，填筑厚度2～5 m。路基典型横断面见图1。淤泥质黏土参数为：

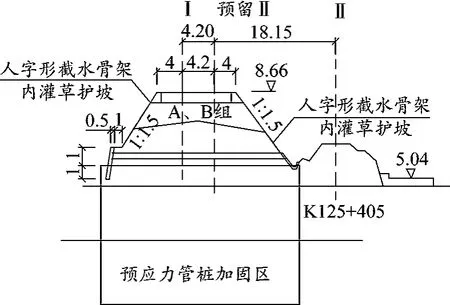
图1 路基典型横断面（单位：m）

需加固路基全长22.9 km。预应力管桩采用PC-500（100）-A型，设计桩身直径0.5 m，壁厚0.1 m，混凝土强度C60，十字钢桩尖，单桩承载力750～1 020 kN。平行于既有路基且距离既有路基5 m和6 m处施打两排预应力管桩，桩间距2.5 m，预应力管桩深度为28～44 m，共需预应力管桩长度为32 969 m。为了防止基础处理过程中对既有线路行车安全的影响，需要对路基加固区段按照《临近营业线施工管理办法》之A类等级进行施工计划管理，并将列车时速限制在60 km内。施工期内需要实时观测既有线路的路基水平位移和路基沉降。

3 数值模型建立

3.1 基本假设

由于压桩过程为高度非线性问题，而且由于压桩数量较多，因此有必要对整个结构进行简化，从而便于计算。基本假设如下：

（1）将整个结构均看作淤泥质黏土一种材质。通过地质资料可以看出，在20 m深度范围内大部分为淤泥质黏土。为了简化计算，只考虑这一种材质。

（2）将整个结构简化为平面应变问题。由于既有路基横截面沿路线方向基本不变，同时预应力管桩为等间距布置，因此整个结构沿路线方向为半无限体。另一方面，由于预应力管桩深度都超过20 m，可以近似认为预应力管桩压入土层后沿不同高度的挤压效果一致。

（3）只考虑预应力管桩完全压入时刻对结构的作用。由于预应力管桩施工是一个逐渐压入的过程，对结构影响最大的时刻为完全压入后的那个时刻。

3.2 数值模拟

本文采用Abaqus 2018建立结构的数值模型见图2。红色区域为原铁路路基所在位置，第一排预制管桩中心距离铁路路基外边缘5 m。模型尺寸为长40 m×宽25 m，共有8 898个单元，9 638个节点。单元均采用平面应变单元CPE4，其为四节点双线性单位，减缩积分，节点为4自由度（两个平动和两个转动自由度）。

图2 结构数值模型

（1）边界条件模拟。模型上缘和下缘采用弹簧单元模拟，弹簧刚度取为淤泥质黏土弹性模量；左侧和右侧边界采用固定约束，即约束节点的平动自由度和转动自由度。

（2）压桩过程模拟。分别在拟压桩位置建立两个半圆形，见图3。半圆直径为0.5 m，两个半圆相切，半圆圆弧端与周围土共用节点，直线段为自由段。在预应力管桩压入中，给定半圆自由段向切点方向的强制位移，位移大小为半圆半径。挤压完成后，在取消强制位移的同时将两个半圆自由段节点所有自由度耦合，从而形成一个整体。由于上、下半圆会存在一个重新找力平衡的过程，因此会有一个微小的位移。同时，当其他桩在挤压土层时，该桩位置也会随之变化，从而模拟出不同桩之间相互作用的过程。

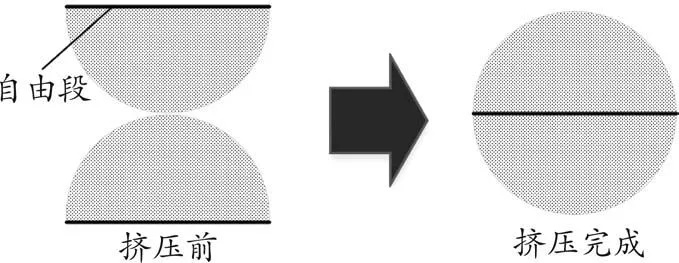
图3 压桩过程模拟

4 工程运用

4.1 模型验证

为了验证本文所建立模型的正确性，分别在距离既有路基5 m处和距离路基6 m处试打两根预应力管桩。两根管桩相距20 m，可以认为两根管桩之间相互无影响。采用本文所构建的数值模型进行计算，分别得到工况1和工况2条件下既有路基位移云图，见图4。由图4可以看出：距既有路基5 m压桩时（工况1），既有路基最大水平位移为4.90 cm，距既有路基6 m压桩时（工况2），既有路基最大水平位移为3.63 cm。

图4 既有路基位移云图（单位：m）

同时，在既有路基上布置水平位移观测点，并将压桩后的位置和压桩前的位置进行对比，得到工况1和工况2下水平位移实测最大值，见表1。

表1 计算最大位移和实测对比

通过表1计算结果可知：（1）工况1和工况2计算值和实测值相差均很小，分别为2.51%和2.25%，可以满足工程精度要求；（2）工况1下既有路基的位移相比较于工况2有明显的增加，说明距离既有路基越近，压桩对既有路基影响越大，且远离1 m大约可降低26%。

4.2 不同压桩顺序对既有路线影响

由4.1节分析可知：距离既有路基不同位置处压桩会产生不同影响程度，且当两根预应力管桩位置较近时会相互影响，因此有必要研究不同压桩顺序对既有线路的影响，从而寻找出最优的打桩路径。在距离既有路基5 m和6 m处分别设置两排共16根桩，桩间距为2.5 m，见图5。分别设计三种打桩工况。

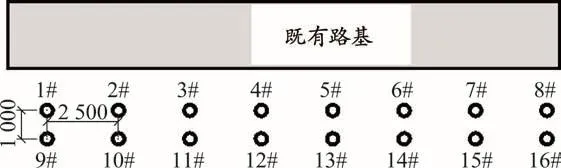
图5 预应力管桩编号（单位：mm）

工况1：先顺序压第一排桩，后顺序压第二排桩，即 1-2-…-8-9-…-16。

工况2：跳打施工，即 1-10-3-12-…-16-8-15-6-…-9。

工况3：先顺序压第二排桩，后顺序压第一排桩，即 9-10-…-16-1-…-8。

三种工况下既有路基位移计算结果见图6；三种工况下既有路基最大位移见表2。

图6 不同工况下的既有路基位移云图

表2 不同工况下的既有路基最大位移

从计算结果可以看出：（1）三种压桩顺序中，位移值最小为工况1的10.08 cm，最大为工况3的10.42 cm，工况1相对工况3减小约3.26%；（2）通过计算可以看出压桩对既有路基位移影响较大，仅通过调整压桩顺序效果较小，必须采取额外的措施来减小对既有路基的影响，比如在第一排桩与路基间设置卸压孔。

5 结束语

当前管桩施工对既有铁路影响研究还局限于实践的经验，并无很好的模拟手段。为了摸清规律，本文开展了管桩施工对既有铁路影响规律研究。首先，将整个结构简化为平面应变问题，并采用强制位移来模拟压桩过程，建立了压桩对既有路基影响的数值模型；其次，通过实际工程验证了数值模型的正确性；最后，通过不同压桩顺序对既有线路的影响开展研究并得出规律。

（1）本文提出的压桩对既有路基影响数值模型具有模拟简单、计算迅速、计算精度高的特点，可用于工程实践。

（2）不同压桩顺序对既有路线有一定的影响，但是影响有限，必须采取额外的措施来减小对既有路基的影响。