多角度理解和运用圆锥曲线性质

方立新 (江苏省扬中市第二高级中学 212200)

刘新春 (江苏省扬中高级中学 212200)

圆锥曲线有许多重要性质，全方位、多角度、整体性地深刻理解这些性质既是学好数学的必然要求，也是提升数学能力和素养的基本载体．

1 理解圆锥曲线性质的本质特征

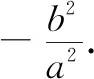
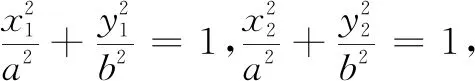
这是椭圆的一个重要性质，双曲线也有类似的性质(略)．以上从数量关系上揭示了椭圆的本质规律，其实圆锥曲线的性质并不是孤立的、一成不变的结论，而是动态的、联系的、可以拓展的．事实上，上述椭圆性质的逆命题也成立，即：

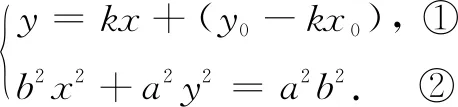
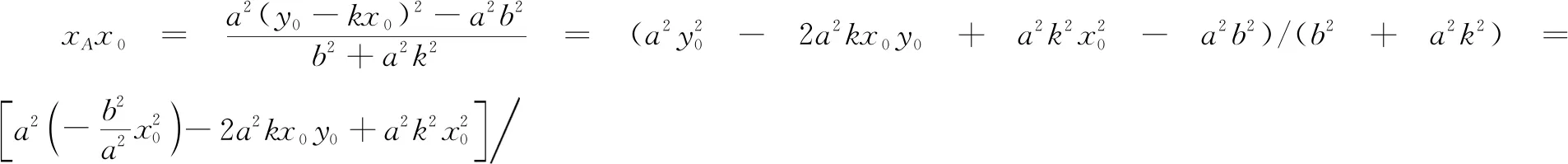
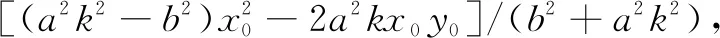
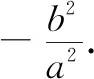
2 领悟圆锥曲线性质的探究方法

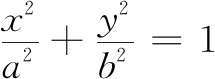
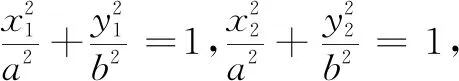
以上结论揭示了椭圆上两点与椭圆中心连线构成的三角形面积与中心弦斜率乘积之间的关系，与椭圆性质的证明采取了类似的方法——点差法和点乘法．应用此结论和椭圆的性质可以解决许多与三角形面积、直线斜率等相关的问题．

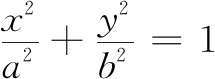
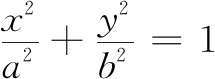
3 掌握圆锥曲线性质的应用策略

同一个知识可能有多种表征形式，而且常常与相对应的方法脱节，在解决问题的过程中往往不能准确快捷地采用相对简捷的方法．我们的策略是，面对待解决的问题，多角度联想概念性质，多形式表征条件结论，多方法简化解题过程，通过观察、比较、尝试、选择获得问题解决．

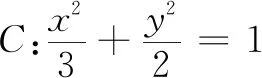
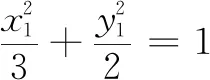
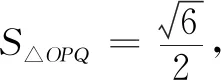
以上结论还可以推广到一般椭圆的情况．对比以上两种解法，不难发现已知结论的作用．

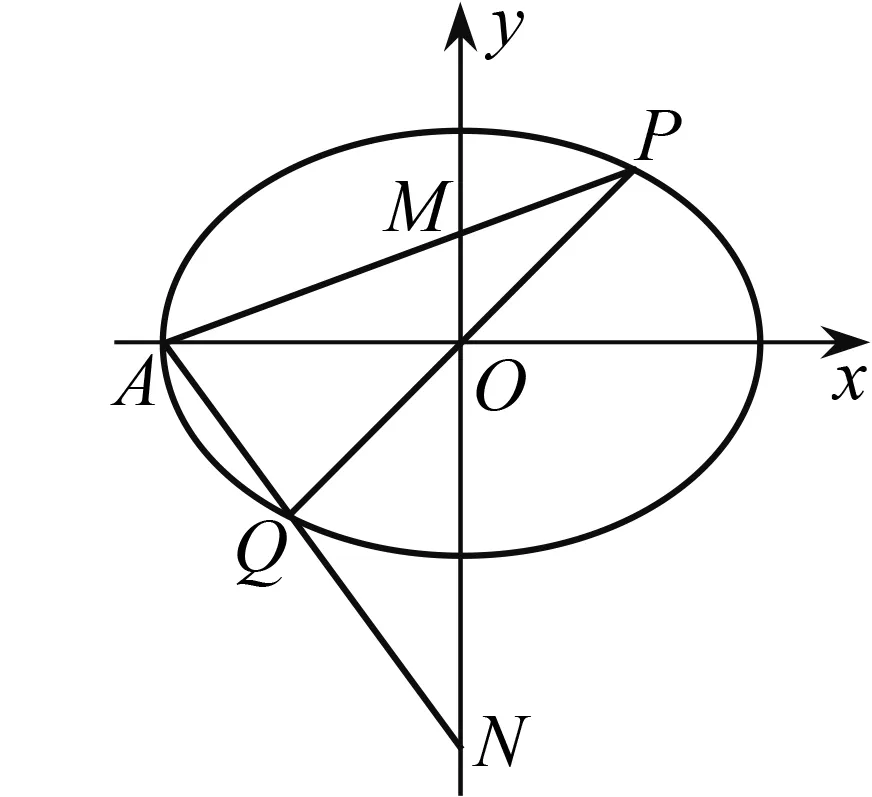
图1

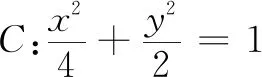
常规解法如下：

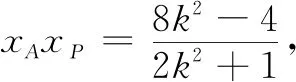
以上两种方法采用“直译法”按部就班求出点M,N的坐标，再求出圆的方程，运算量大，过程繁杂，原因是没有发现题目条件与椭圆性质的本质联系.如果直接假设M,N的坐标再运用中心弦的性质，则可以获得更简捷的方法：