多视角剖析一道2021年高考解三角形问题*

卓晓萍 (福建省莆田第二中学 351131)

蔡海涛 (福建省莆田第二中学 351131 福建教育学院数学教育研究所 350025)

1 试题呈现

(2021年新高考Ⅰ卷第19题)记△ABC的内角A，B，C的对边分别为a，b，c．已知b2=ac，点D在边AC上，BDsin∠ABC=asinC．

(1)证明：BD=b；

(2)若AD=2DC，求cos∠ABC．

本题以三角形为载体，主要考查正弦定理、余弦定理、三角恒等变换等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，考查数学运算、逻辑推理等核心素养，体现基础性和综合性．

本题属解答题中的中档题.高考结束后，笔者随机访谈了部分学生，大部分考生解答此题时都抱有一种想尽快解答的应试心态，但由于紧张而“欲速则不达”，特别在第(2)问未能较快寻找到解决问题的突破口，最后虽然解出来了，但花费了不少的时间.

2 多视角剖析

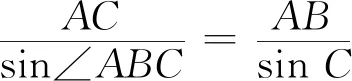
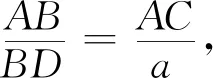
又因为b2=ac，所以BD=b．

评注第(1)问要证明的是边的关系，已知条件含有边、角的关系，因此需要进行边角转化.再根据已知条件中含有∠ABC，∠C，故利用含有这两个角的正弦定理，后续的证明不难完成.

本题的难点在第(2)问，主要有以下视角.

视角1利用函数与方程思想，结合平行线性质，建立方程.

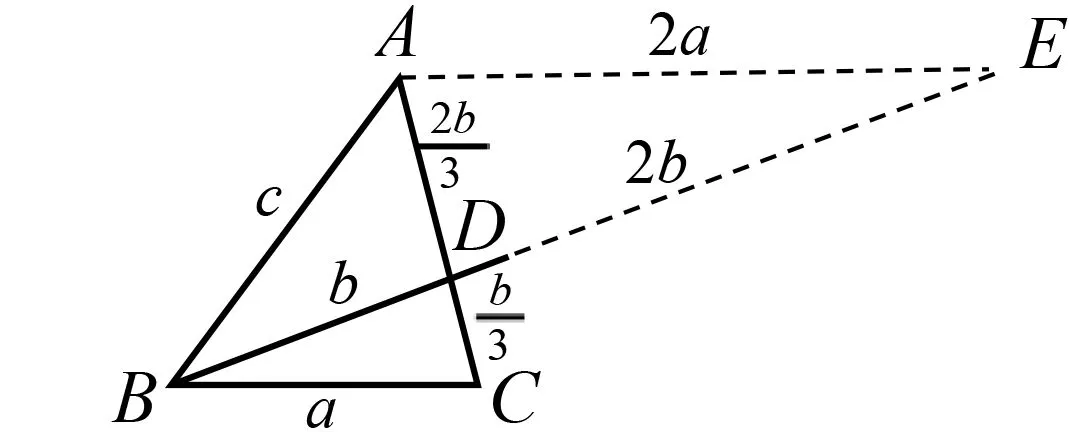
图1

方法1 如图1，过点A作直线BC的平行线AE，延长线段BD，与AE交于点E.因为AD=2DC，所以AE=2a，DE=2b.又∠ABC+∠BAE=π，所以cos∠ABC=-cos∠BAE.

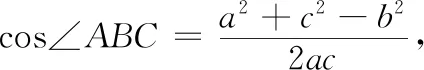
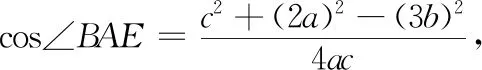
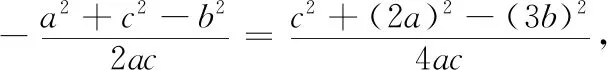
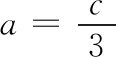
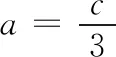
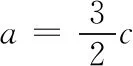
利用本视角还可以有以下方法，碍于篇幅，本文只提供思路，具体解题过程不再赘述.

方法2 如图2，过点D作DG∥AB，利用∠ABC+∠DGB=π，cos∠ABC=-cos∠DGB构造方程.

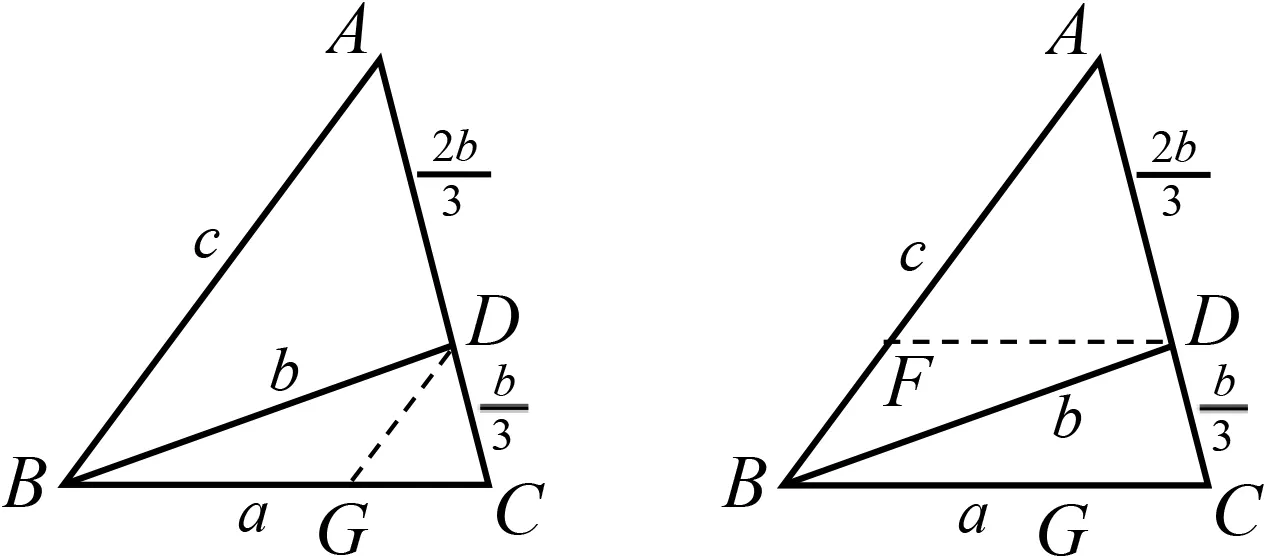
图2 图3

方法3 如图3，过点D作DF∥BC，利用∠ABC+∠DFB=π，cos∠ABC=-cos∠DFB构造方程.

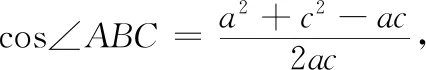
视角2利用化归与转化思想,结合角度关系，建立方程.

方法4 △ABD与△ABC有公共角A，则cos∠BAD=cos∠BAC.

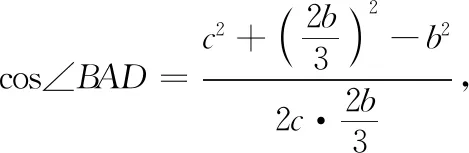
整理得6a2+3c2=11b2，下同方法1.

本视角还可以有以下方法，具体解题过程不再赘述.

方法5 △BDC与△ABC有公共角C，则cos∠BCD=cos∠BCA.

方法6 △ABD与△BDC有一对互补角,∠ADB+∠BDC=π，则cos∠BDA=-cos∠BDC.

评注视角2的思路与视角1的思路类似，都是着力去寻找到用边表示cos∠ABC的表达式，区别之处在于视角2结合了△ABC，△BDC，△ABD之间的角度关系，利用相等或互补关系进行转化.这种方法是解决含多个三角形问题的常用方法.

视角3利用向量的工具性，建立方程.

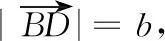
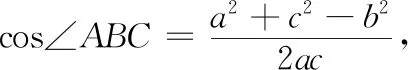
评注向量是高中数学的基础知识，也是解决诸多问题的有力工具，可解决三角形中的角和长度问题.本题即利用向量的模得到一个等量关系.

视角4利用化归与转化思想,把斜三角形化为直角三角形，建立方程.

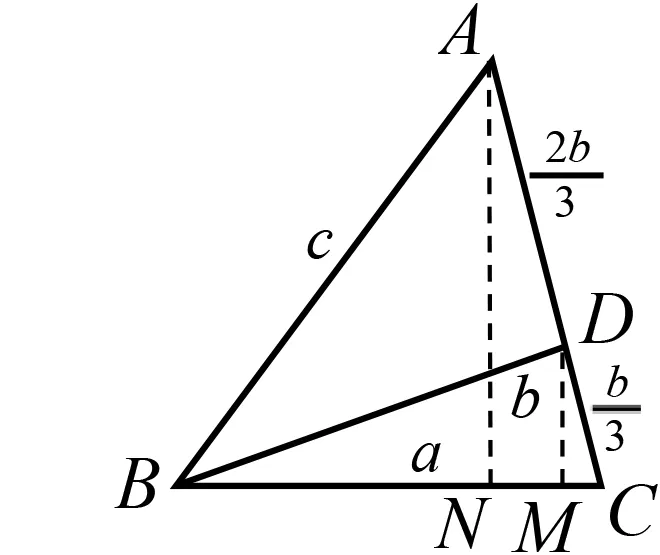
图4

方法8 如图4，过点A作AN⊥BC于点N，过点D作DM⊥BC于点M，设BN=x，CM=y.则CN=3y.

在△ABN和△ACN中，由勾股定理得c2-x2=b2-(3y)2，即c2-b2=x2-(3y)2=(x+3y)(x-3y) ④.

由BC=BN+NC,得x+3y=a⑤.

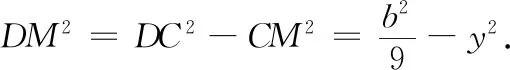
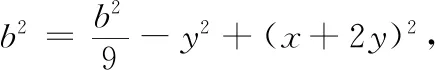
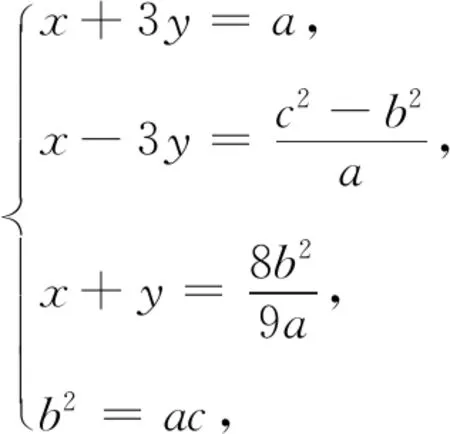
评注一般地，在含多个三角形的复杂图形中,从直角三角形入手会比较简单，因此往往把斜三角形问题转化为直角三角形问题进行处理.

视角5利用海伦公式，建立方程.

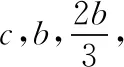
同理可得△BDC的面积为

又因为AD=2DC，所以S1=2S2,得

整理得(25b2-9c2)(9c2-b2)=4(16b2-9a2)(9a2-4b2).将b2=ac代入得

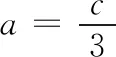
评注由已知条件得△ABD与△BDC面积的关系，又因为要研究三角形三边的关系，故考虑利用海伦公式.

3 教学启示

由以上解答视角不难看出，本题解题的切入点较多，很好地考查了解三角形的有关知识及思想方法，是一道质量较高的选拔性试题.学生的思路不顺畅也告诫我们，教师在教学过程中可引导学生多角度去思考问题.“横看成岭侧成峰，远近高低各不同”，每一种解法背后都有一个故事.教师在展示解法的同时，多让学生去领会其中渗透的数学思想方法，揭示蕴含的数学本质，积累解题经验，从而发展学生的核心素养.