“两个过程”合理性理念下的课堂教学设计——以“三角函数的概念”为例

王 凯 (浙江省杭州市源清中学 310015)

1 问题缘起

2020年11月26日，笔者在参加杭州市某中学学术节的过程中听了两节“三角函数的概念”(2019版人教A版必修第一册5.2节)的同课异构课.第一节课上，A教师以教材给出的框架顺序展开教学，但课堂中学生明显不能很好地跟上教师的节奏来接受知识并给出相应的反馈，学习过程中认知和思维明显不能达到教师的要求，所以不能顺利按教师的引导问题链主动建构三角函数定义；第二节课上，B教师从初中的三角函数定义引出问题，但推广到任意角三角函数的时候，B教师用了一个内燃机传动原理示意图说明任意角三角函数值是随角的变化而变化的实数，这在模型处理上，对学生数学抽象能力的要求过高，即数学知识发生发展的过程欠合理，同样不能很好地切入三角函数概念的主题.

在应用教材进行教学实践时，我们应该用好教材提供的素材，将数学思维的发生和发展过程充分暴露在学生面前，才能吸引学生积极参与知识的再创造和发展的过程[1].既要让数学知识发生发展的过程合理，也要让学生在学习过程中认知的过程、思维的过程合理[2](下文简称为“两个过程”).所以笔者尝试用“两个过程”合理性的理念，对“三角函数的概念”这节课做了一个全新的教学设计，来谈一下如何落实数学核心素养的培养.

2 基于“两个过程”思考下的教学设计

2.1 对教学内容的基本认识

初中阶段利用“边长比”来定义锐角三角函数，这样的定义会让学生对函数一般概念中的“数集到数集”的对应关系产生认知冲突，所以要重新建构三角函数的定义.并且三角函数概念的建构过程与前面各类基本初等函数概念的建构过程都不一样.幂函数、指数函数和对数函数是通过具体实例的共性归纳而抽象出来的，而三角函数概念是直接由单位圆上的点的运动规律的描述得到的.所以在这节课的教学设计中要考虑如何将数学思维的发生和发展过程充分地暴露在学生面前，设计合理的认知冲突，让其参与知识的再创造和发展的过程，既要让数学知识发生发展的过程合理，也要让学生在学习过程中认知的过程、思维的过程合理.

2.2 教学方法的选择

3 课堂实录

3.1 忆初中定义、建认知起点

设问1 同学们，还记得在初中我们是怎样定义锐角的三角函数吗？

设计意图从学生已有的初中知识经验(边长比)出发，着眼于学生的最近发展区，这是学生数学知识发生发展的起点，更是数学思维的发生和发展的起点.

3.2 创设情境冲突，重识研究视角

图1

设问7 此时点P的坐标为.

设计意图借助初中锐角三角函数中熟悉的“边长比”场景，引导学生从已有认知基础出发，创设情境冲突，让学生用任意角的研究策略来重新认识初中的定义，为单位圆的引入做好铺垫.这个过程是学生对原有知识进行再认识，为再创造提供了基础，也让学生在学习过程中提升了自己原有的认知和思维.

3.3 特殊走向一般，完成知识建构

设问11 根据这样的想法，对一个任意角α(α∈R)的正弦、余弦和正切，该如何定义？

设问12 根据这个定义，任意角α(α∈R)的正弦、余弦和正切是否都存在？

接下来师生共同得到三角函数的定义．

设计意图在锐角三角函数的具体情境的引领下自然地引入单位圆来定义三角函数，让学生感受数学概念、数学方法与数学思想的起源与发展都是自然的，不仅合情合理，甚至很有人情味[3].

在概念建构的过程中让学生体会三角函数是“α与x，y直接对应”，无须计算.虽然α，x，y都是实数，但实际上是“几何元素之间的对应”.整个过程让学生参与了知识发展的过程，不仅使三角函数定义的引入水到渠成，也让学生对函数的本质有了更深入的思考.这培养了学生的逻辑推理和数学抽象素养，使之经历从具体到一般的数学抽象过程，切身体验知识的再创造和发展的过程，其认知过程和思维过程可以得到新的发展.

3.4 问题引领思考，新知认识深入

设计意图借助问题再次理解三角函数是“α与x，y直接对应”，无须计算.认识到三角函数的“对应关系”是“几何元素之间的对应”.

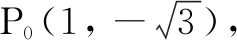
问题4设α是一个任意角，它的终边上任意一点P(不与原点O重合)的坐标为(x,y)，点P与原点的距离为r，试用x,y和r来表示角α的正弦、余弦和正切值.

图2

设计意图用问题链的形式引领学生思考新的定义，通过问题让学生体会初中阶段用“边长比”到直角坐标系上的“坐标比”，最后回到单位圆来计算三角函数值，本质上是等价的，说明了我们的新定义和初中的定义是一脉相承的，是初中定义的继承和发展.让学生体会数学概念的形成过程是水到渠成、浑然天成的产物[3]，并在这个过程中培养学生逻辑推理和数学抽象的核心素养.

3.5 课堂小结

设计意图再次回顾本节课的研究思路，感受从初中“边长比”到高中“单位圆”的变化，体会概念在不同认知阶段会有不同的认识深度.

3.6 课堂练习

设计意图通过这组课本练习题(179页到180页的练习的1～3题)，让学生学会用这节课所学的三角函数的概念来求三角函数值，在这个过程中强化其直观想象和数学运算的核心素养.

3.7 课堂拓展

(课本180页练习第4题)：已知点P在半径为2的圆周上按顺时针方向做匀速运动，角速度为 1 rad/s，求2 s时点P所在的位置.

设计意图让学生反思整节课研究问题的路径，寻求一种问题解决的范式，让其自己能建立一个问题研究的体系，进而合理地解决问题.进一步培养学生的逻辑推理和数学抽象的素养.

4 课后反思

整个设计以明暗两线进行，重视“概念”的生成.明线是通过具体已知锐角三角函数定义推广到任意角三角函数的定义，让学生在过程中归纳现象和抽象结论，得到一般化的结论，即学生的数学知识发生发展的过程；暗线是通过初中锐角三角函数“边长比”和函数一般概念的认知冲突，带领学生走向高中“单位圆”的定义，在过程中帮助学生掌握一类问题的研究范式，领悟数学的本质，即学生认知和思维的过程发展.

人教A版高中教材在其主编寄语中说道：“数学的特点是逻辑严谨，从概念到性质再到应用环环相扣，前面的知识未理解，后续的学习就必然遇上实质性的困难.学数学，既没有捷径，也没有灵丹妙药，唯有按照数学的方式，按部就班，循序渐进地想，在基础知识上下足功夫，才能取得好成效.”[4]这节课的设计也体现了这种思想，基于“两个过程”合理性的思考，让学生从已有的认知出发，在明(知识)暗(认识和思维)交错中，重识认知冲突，建构新的认知结构，学会迁移后进行新的诠释，最终使学生的核心素养在“两个过程”中落地.