深刻理解 深入挖掘 实施运算*——以2021年新高考全国I卷第21题为例

周 炎 (江苏省平潮高级中学 226361)

解析几何是高中数学的主干知识，它紧扣曲线方程、数量关系、几何图形、数形结合等主线，让学生深刻体会到从方程出发用代数方法研究几何问题这一解几本质．在历年的全国高考数学试卷中，解析几何试题一直占据着举足轻重的地位，考生在该题上的成败是决定其最终数学分数高低的重要因素之一．《普通高中数学课程标准(2017年版)》明确指出了平面解析几何解决问题的基本过程，即根据几何问题和图形的特点，用代数语言把几何问题转化为代数问题；根据对几何问题(图形)的分析，探索解决问题的思路；运用代数方法得到结论．笔者以课标精神为引领，对2021年新高考全国I卷第21题第(2)小题进行剖析，逐步发现、优化、解决问题．

1 试题呈现

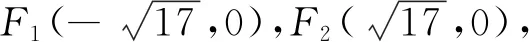
该题考查双曲线的定义和方程、直线与双曲线的位置关系，考查数形结合思想、逻辑推理能力与数学运算能力．第(1)小题既可以由定义法确定曲线为双曲线的右支，从而确定方程，还可以用直接法进行代数推理求得曲线方程．第(2)小题是过动点的两直线与双曲线相交，当截得的线段长乘积相等时，研究两直线斜率和为定值问题，对学生的思维能力及运算素养提出较高的要求，具有较好的区分度．

2 解法剖析

2.1 立足双基，在熟悉的情境中转化几何问题

思路1题干中的TA·TB=TP·TQ是学生熟悉的直线被曲线所截的弦长问题，如何表示TA·TB是解题的关键，联想到弦长公式，结合设而不求思想，借助韦达定理可解决问题．

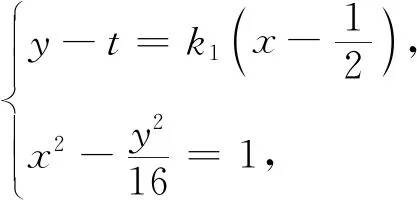
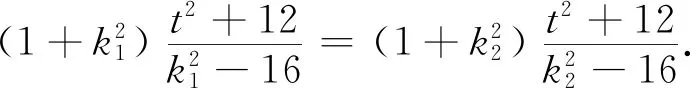
反思 已知直线过一点，常规想法是设出直线的点斜式方程，与曲线方程联立，消元整理．但此时不难发现直线方程表达式不够简洁，整理时运算量大，容易导致计算错误，故联想到直线方程的斜截式．

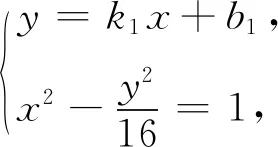
余下过程同解法1.

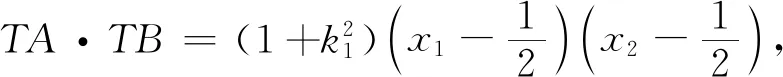
点评以上三种解法，基于同一数学情境，运用相同数学知识与技能，但在实际解决问题时存在一定差异:解法1根据问题特征形成合适的运算思路，解决问题，属于数学运算素养的初级水平；解法2针对运算问题，合理选择，属于中级水平；解法3能够体会运算法则的意义，构造运算程序，解决问题，是数学运算素养的高级水平．

2.2 理解数与式，在关联的情境中转化几何问题，实施数学运算

思路2本题情境为过一点的直线与曲线相交，研究该点与交点连线的线段长问题．对于这样的问题，有时我们还采用“将几何问题转化为向量问题”的方法．联想到“坐标系与参数方程”中直线参数方程里参数的几何意义——有向线段的数量，因此设直线的参数方程，与曲线联立，直接得到两条线段的长度乘积．

(16cos2α-sin2α)l2+(16cosα-2tsinα)l-(t2+12)=0.

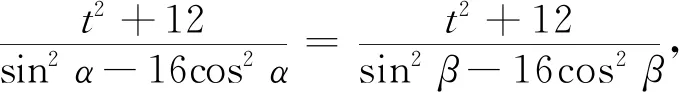
因为cosα≠cosβ，α∈(0，π)，β∈(0，π)，所以cosα=-cosβ，sinα=sinβ，则有tanα=-tanβ，所以k1+k2=0．

点评参数方程是研究曲线方程的基本工具，是表示曲线的另一种形式，它弥补了普通方程在表示曲线方程中的不足．思路2是在明晰题目背景的基础上对问题进行代数及几何角度的思考，进而选择设直线的参数方程，直接表示出TA·TB，在一定程度上简化了运算，体现了参数方程的灵活性，是一次“数”与“形”的完美结合．

2.3 挖掘代数式的几何特征，在知识迁移中转化几何问题

思路3对条件进行类比迁移，研究代数式TA·TB=TP·TQ，发现与平面几何中圆幂定理形式相同，确定A，B，P，Q四点共圆．进而重新构建运算程序，借助圆的一般方程的代数特征进行运算推理．

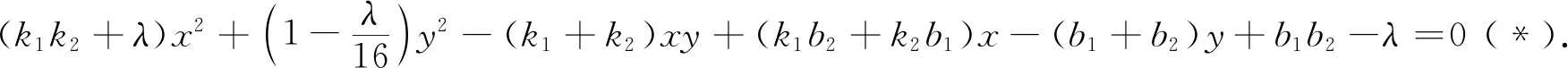
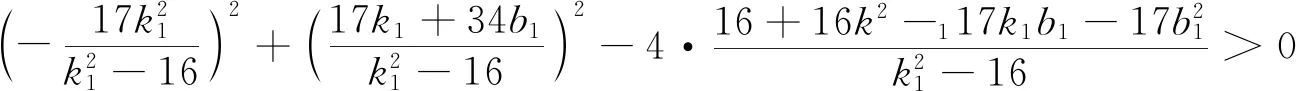
点评对运算情境内涵的深刻挖掘促使我们综合运用所学数学知识、思想方法，将问题迁移到不同情境中去．此种做法巧用平面几何知识，将弦长问题巧妙转化，回归解析几何的本质．

3 反思与启示

3.1 夯实基本知识与技能，做到心中有“型”

纵观历年全国高考数学卷解析几何主观题，重视对基本概念、基本方法、基本技能的考查．高中数学课程标准突出“四基”可能要比突出“数学核心素养”更容易操作一些，更有利于指导高中教学．因此，高中数学解析几何教学不能仅是简单的刷题，应加强对基本概念的理解，如本题第(1)问，抓住双曲线的定义则能迅速求解；同时，通过有针对性的技能训练帮助学生熟练掌握基本方法、常见数学模型，如第(2)题，利用弦长公式、结合韦达定理解决线段长问题就是解析几何中的基本方法与模型．

3.2 提升学生数学思维力，做到手中有“术”

解析几何试题命制注重数学的本质与通性通法，入口较宽，容易找到解题思路．如本题的思路1，是绝大多数学生能想到的基本做法，若能对常规运算程序做多次之想，如思路1的三种不同处理，则可大幅提升运算速度及正确率．这就要求教学时，不能局限于找到解题思路，还应花大力气帮助学生对算法程序进行比较、分析，促进学生运算素养的发展．在有了一种基本解题思路后，我们还应当引导学生对几何问题(图形)进行深度挖掘、多角度审视，以探究出其他不同解法，如这里的思路2和思路3．这样既能让每位学生找到最适合的、最擅长的解题方法，又能帮助学生看清问题本质，进而提升学生的数学思维能力，真正做到手中有“术”．