一种球面地形重力位的计算方法

朱化强

(贵州师范大学物理与电子科学学院，贵州 贵阳 550025)

在月球和类地行星表面地形重力异常的估算中，早期研究采用低阶次近似，常常导致较大的误差[1].在直角坐标系中采用高阶近似，可以得到较好的精度[2]，被广泛地应用于重力异常的正反演问题[3-5].这种高阶近似算法，主要依据快速傅里叶变换，通过地形频谱即可以迅速求解相应的重力异常，再经过傅里叶逆变换即可求得研究区域表面地形引起的重力异常.这种方法不但能保持快速计算，还便于重力异常信息的滤波处理，具有较大的实用价值，在地球物理研究中被广泛地应用[3-5].随着月球探测数据的增加，发现诸如月球这类小天体，其曲率产生误差将不能被忽略[6-7].文献[2]的模型对月球和火星这类小天体重力异常的正反演，会产生不可剔除的模型误差，导致结果解释不合理等现象[6-7].近年来，随着火星和月球探测活动的开展，相关重力数据越来越丰富[8-9]，有必要构建适用于这类小天体的球坐标重力正反演模型.为此，本文提出一种球面地形重力位的估算方法，以期为小天体重力正反演提供一定的参考.

1 直角坐标平面模型的重力位

参考文献[2]，假设直角坐标系下平面模型的重力位为Δg，产生该重力位的地形高程为h(r)，对两者进行傅里叶展开，可得重力位的傅里叶变换F[Δg]与n阶ρ地形傅里叶变换F[hn(r)]的关系为

其中，r表示坐标原点至地形参考点的位置矢量，n表示傅里叶展开的阶数，z0表示参考平面的位置高阶，k表示波矢量，G表示万有引力常量，ρ表示地形密度.上式对于大天体而言，界面地形的重力位因界面弧度的影响较小，但对小天体而言，地形界面因弧度对重力位的贡献必须考虑进去.

2 球面地形的重力位

如图1所示，假定天体的球心为O，平均参考半径为R，相对该参考球面距离为h(θ,φ)的地形点B(半径为r).对于半径为r0的参考球面(r0>R)的点A，点B对点A的重力位为(如图1虚线所示)

(1)

其中，ρ(r,θ,φ)表示天体表面地形的密度函数，G为万有引力常量，dV表示天体表面地形的体积微元；r0和r分别表示点A和点B的径向矢量，两矢量的夹角为γ，两矢量差的模为|r-r0|.

图1 界面地形重力位估算示意图

假定表面地形的密度为常数，即ρ(r,θ,φ)=ρ0，并考虑到勒让德多项式母函数的关系[10-11]，以及积分与求和进行互换，对式(1)在径向进行积分得

UA(r0,θ0,φ0)=

Rn+3]Pn(cosγ)sinθdθdφ

(2)

上式中，Pn(cosγ)表示n阶勒让德多项式.利用二项式公式，可以将式(2)进一步化简成

UA(r0,θ0,φ0)=

(3)

(4)

为了进一步化简式(3)，参考文献[10]，将n阶勒让德多项式Pn(cosγ)表示成n阶m次正则化球谐函数Yinm的关系，即

(5)

其中

(6)

上式中，Pnm(cosθ)表示正则化的n阶m次连带勒让德函数，cosmφ和sinmφ表示余弦和正弦函数，θ和φ分别表示余纬度和经度.参考文献[12]，正则化的球谐函数Yinm满足如下正交性原则

(7)

上式中狄拉克函数δnl和δmk满足如下关系

(8)

如图1所示，参考文献[3-5，10]可将地形高程h(θ,φ)展开l阶p次成球谐函数的形式，假定地形高程球谐展开系数为hilp，即

(9)

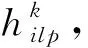
(10)

(11)

将式(11)代入式(3)，顾及式(5)—(8)，可得

(12)

(13)

其中，M表示天体在参考半径R内，平均密度为ρ0的总质量，而且必须满足r0>r.

3 讨论与应用

有关地形引起的重力位，其位系数式(13)涉及求和运算，而且随着阶次n的增加，计算量不断增大，但这实际上没必要考虑太多高阶项.式(13)来源于式(4)，其中h/R表示表面地形高程与天体平均半径的比值，此项的值一般较小，特别是对于高阶项.以火星表面最高的奥林匹斯山(Olympus)为例，其高程接近22 km[12-14]，而火星的平均半径为3389.5 km[15]，h/R的高阶项趋近于零，一般计算时不超过7阶.图2表示求和项式(4)中每一项的值随k和n的分布，由图可知，当k超过5时，式(4)的高阶项几乎没有变化.图3表示式(4)中所有项之和，由图可知，对于同一个球谐阶数n，k取k=3和k=7时并没有太大的区别，因此，实际应用中，式(4)的求和项数最多取前7项即可满足精度要求.

图2 重力位求和式(4)中每一项随k和n变化图

图3 重力位求和式(4)随k和n变化的总和分布

为了应用本文算法，参考文献[16，17]，取火星行星壳密度ρc=2900 kg·m-3，取火星重力位参考球面半径r0=3396 km[17]，地形数据取自文献[16].在计算过程中取式(13)最大求和项数为5项，火星表面地形产生的重力位分布如图4所示，其投影中心坐标为(-90°W，0°E)，左边是火星表面著名的奥林匹斯山脉(如图4白色区域所示).图4表明火星北半球的重力位明显低于其南半径，这主要是由于北半球因低洼的盆地产生负的重力位，而南半球因高原产生正重力位所致，这与火星表面如文献[16]给出的地形特征一致，表明本文构建的算法具有一定的合理性.

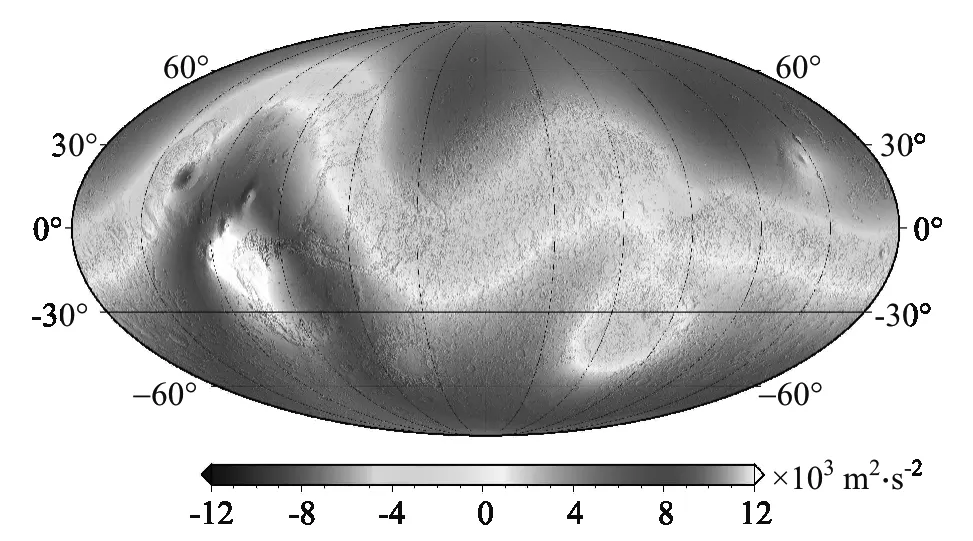
图4 火星表面地形取火星壳密度2900 kg·m-3时的重力位分布

为了比较直角坐标模型与本文球谐模型的差异，图5给出了本文算法的重力位UA与直角坐标平面模型重力位Δg的差值UA-Δg.火星南半球为高地，北半球为平原，赤道附近聚积了较多火山.图5表明两种算法对两极，以及赤道附近火山区域重力位的计算存在一定的偏差.文献[18]的研究表明，火星扁率对其重力位的影响较大.图5也显示两种算法的重力位在两极存在一定的差异，表明火星表面曲率对重力位的影响不能忽略.因此，本文基于球坐标系推导的球谐模型更适合于球状天体表面地形重力位的估算.

图5 直角坐标模型与本文球谐模型求解的重力位偏差图(火星壳密度取2900 kg·m-3)

4 结论

由于月球和火星此类小天体曲率特征的影响，目前地学界常用的直角坐标模型不适合于这类小天体的重力位估算.特别是近年来火星和月球探测数据越来越丰富，有必要构建适用于这类小天体的球坐标重力正反演模型.本文基于牛顿引力位理论，应用球谐变换对重力位进行展开，通过特定的数值推理，发现表面地形引起的重力位可以用地形的高阶展开系数直接计算，进而简化了传统数值积分复杂的求积过程.同时，研究发现高阶地形产生的影响不超过7阶，在实际应用过程中取5阶以内的高阶地形就能满足精度要求.