基于图像复原技术与约束最小二乘方滤波器的绝缘子表面电荷反演算法

2021-09-16潘子君郝留成王亚祥

电工技术学报 2021年17期

潘子君潘成唐炬郝留成王亚祥

（1. 武汉大学电气与自动化学院武汉 430072 2. 平高集团有限公司平顶山 467001）

0 引言

近年来，高压直流输电技术以其输送容量大，可靠性高，环境兼容性好等优势在远距离电能传输、新能源接入以及大规模电网互联等方面备受关注[1-3]。但随着电压等级的提升与运行范围的扩大，以直流气体绝缘组合电器（Gas Insulated Switchgear, GIS）和气体绝缘输电线路（Gas Insulated transmission Line, GIL）为主的气体绝缘设备的大范围应用与推广仍存在一定的障碍与技术瓶颈[4-5]。主要原因在于，长期单极性直流电场作用将促使固体绝缘的表面传导和体传导以及气体侧的微放电等来源途径产生的大量自由电荷沿直流电场方向，不断地积聚在绝缘子表面[6-8]，进而导致气-固界面局部电场畸变而引发绝缘子沿面闪络。这将大大降低设备的绝缘等级，从而影响其运行的安全性与稳定性。因此，准确地测量绝缘子表面电荷分布特性，进而研究其聚散机理与调控策略对高压直流气体绝缘设备的科学设计与安全运行具有重要意义[9]。

目前被广泛采用的有源静电探头[10-11]虽然能有效检测表面电位分布大小，但无法直接定量表征表面电荷密度分布[12]。因此，在全面掌握绝缘材料表面电位分布的基础上，研究者们通过建立电位测量值与电荷密度分布之间的关系，即电位-电荷转换矩阵，来开展表面电荷反演计算，进而获取绝缘子实际表面电荷密度分布[13]。

早期，D. K. Davis等认为电位分布与电荷密度分布之间呈线性关系，进而提出了基于线性标度的表面电荷反演算法[10]。该方法未考虑整个材料表面积聚电荷的综合影响，且假设静电探头测量系统的等效电路中各电容值保持不变[12]。而T. Takuma等的研究表明，该方法仅适用于厚度小于5mm的薄层试样，在针对厚度较大材料的表面电荷检测过程中，会因等效电容值变化以及整体积聚电荷的相互影响而引入较大误差[14]。近年来研究者们利用有限元思想，将待测试样表面剖分为若干区域，利用电场数值计算来考虑绝缘子表面积聚所有电荷对每个剖分区域电位分布的影响。基于此，涌现了多种表面电荷反演算法，包括视在电荷法[15]、λ函数法[16]、φ函数法[17]等。但这些方法在计算过程中均需要进行电位-电荷转换矩阵的求逆运算，而大型矩阵的求逆往往存在不适定问题，即使转换矩阵或电位分布矩阵中存在很小的扰动，也会在计算结果中引入较大的误差[18]。针对这类问题，研究者们通过借鉴维纳滤波中的最小方均误差估计准则对计算过程进行优化[18-20]。该方法基于Tikhonov正则化原理，以系统输出与期望之间的均方误差最小为计算准则[21]，求解表面电荷密度分布的估计解。这种方法有效改善了因电位-电荷转换矩阵维数过大而存在的矩阵求逆不适定问题，大大提升了计算精度与算法稳定性，对盆形或锥形绝缘子这类平移改变系统中的表面电荷反演有着良好的计算效果。

而针对几何模型为平板的这类平移不变系统的表面电荷反演，上述算法还存在一定局限性。因为当测量点数为N时，一般需要进行N×N次电场数值计算以求取电位-电荷转换矩阵。而盆形或锥形绝缘子的几何形状为旋转对称结构，其电位-电荷转换矩阵为分块循环矩阵，这大大减少了转换矩阵求取过程中的电场数值计算次数。但平移不变系统的电位-电荷转换矩阵为实对称矩阵，必须进行N×N次数值计算才可获取转换矩阵的所有信息[22]。这导致计算量十分庞大，在测量点数较多的高空间分辨率测试环境中难以应用。针对这类问题，研究者们基于图像处理技术提出了针对平移不变系统的表面电荷反演算法[23-24]，该方法采用二维傅里叶变换将空间域中向量的卷积运算转换为频域中的乘积运算，在规避了多次电场数值计算的同时省去了大型矩阵的求逆过程，并利用维纳滤波器以抑制噪声干扰，进而获取表面电荷密度分布的估计解。目前这种算法存在的问题是，维纳滤波器的滤波系数需要通过获取噪声功率谱与未退化图像功率谱的比值来确定，但实际功率谱往往很难获取。实际操作中大多采用某一特定的常数K作为滤波系数的替代值，通过人为调整K值，以获取一个较好的反演结果。但人为选择滤波系数会引入较多主观因素，且存在选择效率较低，选择方式不统一等问题。因此，后续有必要对频域中的滤波器构建过程进行优化，研究滤波系数的自适应选择手段，提升算法的精度与可靠性。

综上所述，本文提出了一种针对“平移不变系统[20,23]”的表面电荷反演算法，借鉴图像复原技术的处理思路，在结合二维傅里叶变换的基础上利用约束最小二乘方滤波器（Constrained Least Square filter, CLS-fliter）抑制噪声干扰，通过迭代手段来自适应地获取滤波系数的最优解，最终实现表面电荷密度分布的反演。本文详细介绍了该算法的设计思路与实现流程，并在讨论算法精度的基础上将其与维纳滤波反演和模拟电荷反演算法进行了对比，最后通过实验验证了算法的有效性。

1 表面电荷反演理论

1.1 图像复原技术

在图像复原领域，把原始图像经传递函数作用与外界噪声干扰后得到输出图像的过程称作图像的退化，而利用输出图像反推至原始图像的过程称作图像的复原[25]。其中，传递函数即是上述过程中的退化模型。图1显示了图像退化与复原的过程。

图1 图像退化与复原过程Fig.1 Process of image deterioration and restoration

因此，空间域中图像的退化过程可表示为[25]

式中，*表示空间卷积；g(x,y)为退化后的图像；h(x,y)为退化模型H在空间域中的函数表示；f(x,y)为原始图像；n(x,y)为噪声函数。

当给定关于H和n(x,y)的相关知识后，图像复原的目的即为利用g(x,y)获取原始图像f(x,y)的估计解，因此图像复原过程可表示为[25]

式中，C为复原函数的空间域表示。

1.2 表面电位-电荷转换关系的建立

将待测绝缘子表面分为N个区域，则表面电位ϕ与表面电荷密度σ之间满足矩阵关系[26]为

式中，电位-电荷转换矩阵H中的元素hij为待测绝缘表面上第j个测量区域内单位电荷密度对第i个测量区域内表面静电位的贡献值。

针对“平移不变系统”而言，其响应与激励施加于系统的位置无关[27]，即待测试样表面沉积的电荷引起的电位分布与该电荷所处的材料表面位置无关，则利用平移不变性质可将式（3）改写为[20]

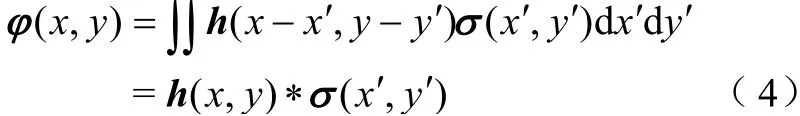
式中，σ(x′,y′)为坐标(x′,y′)处的表面电荷密度；h为卷积核；h(x−x′,y−y′)表示(x′,y′)位置的单位电荷在测量点(x,y)处产生的感应电位。

由卷积定理可知，空间域中的卷积可等价为频域中的乘积运算[25]。对式（4）进行二维傅里叶变换为

式中，U(u,v)、H(u,v)、Q(u,v)分别为ϕ(x,y)、h(x,y)、σ(x,y)在频域中的傅里叶变换表达式。则频域中的表面电荷密度分布为

对式（6）进行二维傅里叶逆变换即可获取空间域中的表面电荷密度分布的估计解。但实际测量中会不可避免地引入噪声干扰，直接采用式（6）计算将无法排除噪声信号对目标图像的干扰，影响最终图像复原精度。因此，有必要针对测量结果进行滤波处理以抑制噪声干扰。

2 CLS-Filter表面电荷反演算法实现

2.1 约束最小二乘方滤波器

本文通过在频域中构建约束最小二乘方滤波器（CLS-filter）抑制噪声干扰，进而实现表面电荷密度分布的反演。

在测量平移不变系统的表面电荷过程中，可将式（1）可改写为向量-矩阵形式为

式中，ϕ、H、σ、n分别为ϕ(x,y)、h(x,y)、σ(x,y)、n(x,y)的向量-矩阵形式。

此时约束最小二乘方滤波的约束准则可定义[25]为

由上述准则可推得约束最小二乘方滤波器的频域表达式为[25]

式中，H∗(u,v)为H(u,v)的共轭矩阵；β为滤波系数；P(u,v)为拉普拉斯算子的傅里叶变换[25]。

综上所述，经约束最小二乘方滤波器处理后的表面电荷密度分布图像复原的估计解为

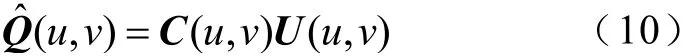
2.2 滤波系数的自适应求解

与维纳滤波器类似，本研究所述约束最小二乘方滤波器也可通过手动调参来交互式的选取滤波系数，以获取一个视觉上可接受的图像复原结果。但手动选取参数往往不能获取图像复原的最优解，且计算效率较低。在已知干扰噪声参数的条件下，可采用迭代算法实现对滤波系数取值的筛选，以进一步提升图像复原精度。

根据式（8）所述约束准则，定义误差向量为

则式（8）可改写为

式（13）中，α取值越小，迭代结果的精确度越高。当精确度因子为零时，迭代结果严格满足式（12）。在指定滤波系数初值的基础上计算误差向量r的欧式范数r2，并结合式（13）迭代调整滤波系数大小，直到满足迭代约束条件。

为完成上述迭代过程，需要对r2与n2值进行求解，即求解r(x,y)与n(x,y)。对r2而言，式（11）在频域中的表达式为

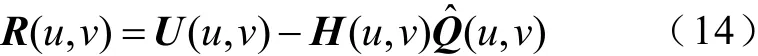
因此，可通过计算R(u,v)的值，并对其进行傅里叶反变换来获取迭代过程中的r(x,y)，而对噪声信号n(x,y)向量的欧式范数而言，只需获取该噪声信号的均值与方差即可求解[25]。

2.3 算法流程与实现

综合2.1节与2.2节所述，图2给出了基于滤波系数迭代的CLS-filter反演算法流程。本文将表面电荷的反演过程分为滤波器函数的建立与滤波系数的求解两步。具体地，本节以平板绝缘试样为例详细介绍该算法的计算过程，圆柱或圆管试样等平移不变模型本方法同样适用。

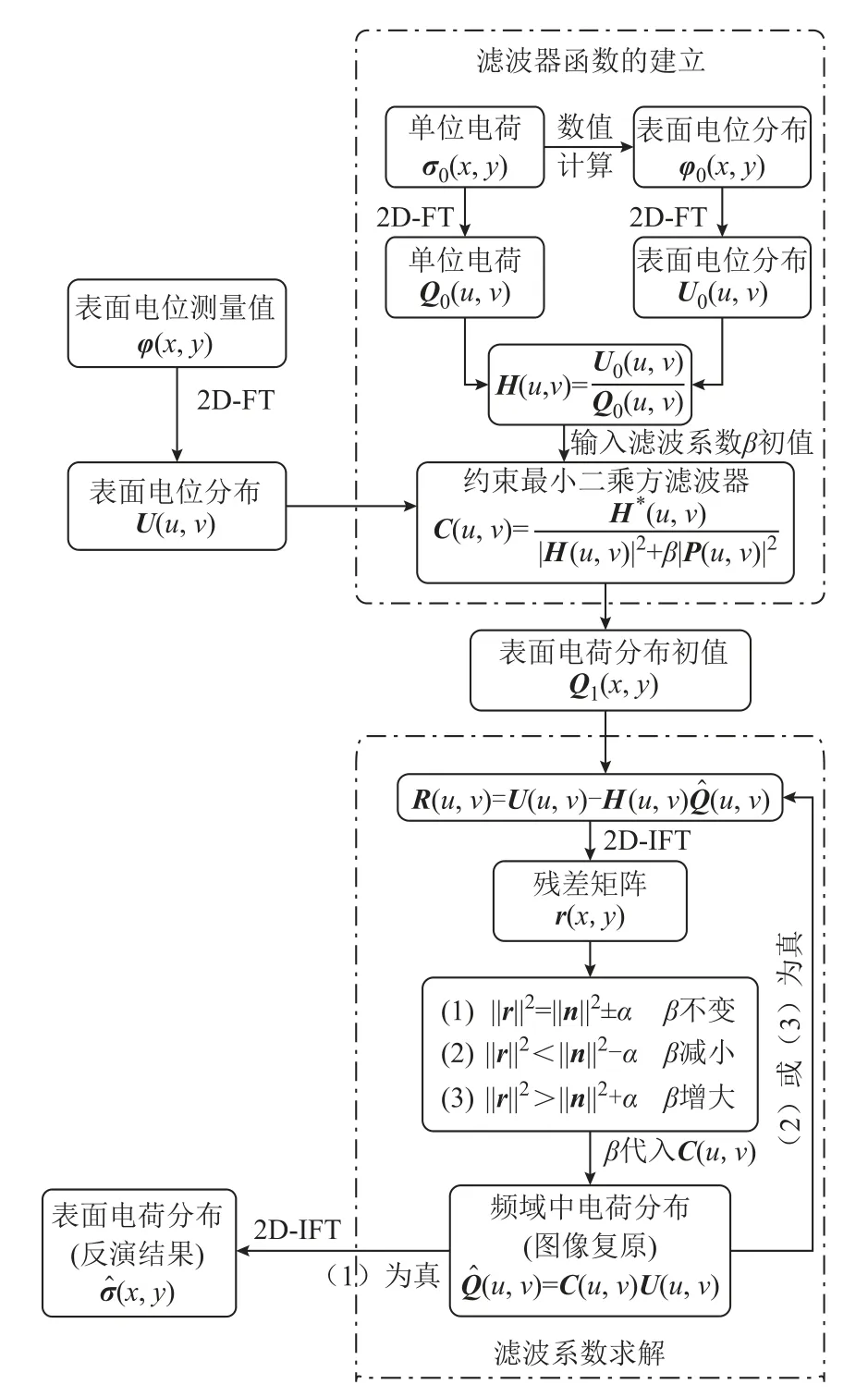
图2 CLS-filter反演算法流程Fig.2 Flowchart of inversion algorithm based on constrained least square filter

首先，通过在待测试样中心处设置单位电荷密度来模拟系统的冲击响应，进而获取传递函数在频域中的表达式。假设待测试样为一厚度3mm的环氧树脂板，测量区域面积为45mm × 45mm。这里设置每个测量点间距1mm。在COMSOL Multiphysics中按实际试样大小建模，在位于试样表面几何中心测量点处设置单位电荷密度σ0(x,y)为1C/m2，并计算此时试样的表面电位分布ϕ0(x,y)，如图3所示。对σ0(x,y)、ϕ0(x,y)进行二维傅里叶变换（2D-FT），代入式（6）求得传递函数H(u,v)与系统逆滤波器1/H(u,v)的表达式，基于此作出了二者在频域中的二维幅频特性分布图。

图3 单位电荷设置条件下的表面电荷与电位分布Fig.3 Surface potential and charge distribution caused by a unit charge

系统函数在频域中的二维分布如图4所示，系统传递函数的幅频响应随频率增大逐渐减小，到高频区域收敛至一较小值。因此，系统逆滤波器的幅频响应将在高频区域展现为一较大值。而系统逆滤波器的幅频特性分布则表现为从低频到高频逐渐增大，在高频区域呈现发散状态，且分布图谱的幅频响应在高频区域达到了10-7量级，而低频区域仅为10-9~10-8。若直接采用逆滤波反演将使高频噪声被放大近100倍，甚至淹没测量信号。因此，所构建CLSfilter需为一低通滤波器以实现对高频噪声的抑制。

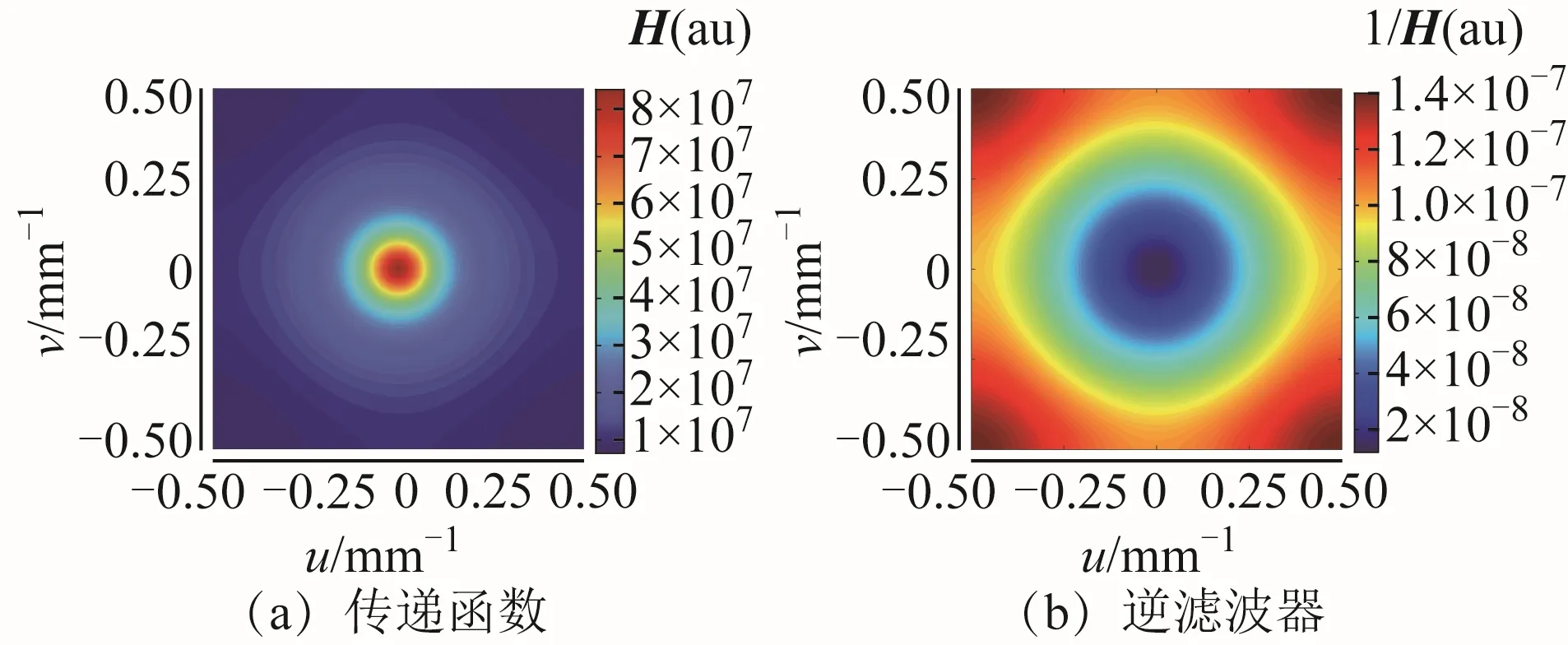
图4 系统函数在频域中的二维分布Fig.4 Two-dimensional distribution of system function in frequency domain

为研究该算法的计算精度，本文利用仿真算例来模拟实际测量中的计算过程。具体地，在COMSOL Multiphysics 中设置待测试样表面电荷分布，并叠加一定干扰信号来模拟实际测量中引入的噪声干扰。设置“WHU”形状电荷分布，每个字母电荷密度大小依次为：1C/m2，0.5C/m2，1C/m2，并计算此时试样表面电位分布，如图5所示。另外，通过在表面电位分布图谱上叠加高斯噪声来模拟实际测量引入的噪声信号。高斯噪声均值为零，标准差设为表面电位最大值的0.5%。本文令精确度因子α=0.01对上述算例开展反演计算。

图5 模拟设置的表面电荷与电位分布Fig.5 Simulated surface charge and potential distribution

图6 所示为迭代所得CLS-filter传递函数C(u,v)的幅频特性分布图，可见其增益幅度随频率上升呈现先增大后减小的趋势，在高频段增益幅度被明显抑制, 此时约束最小二乘方滤波器为一低通滤波器。将迭代所得C(u,v)函数代入式（10）并进行二维傅里叶反变换，即可获得反演后的表面电荷密度分布。

图6 约束最小二乘方滤波器在频域中的二维分布Fig.6 Two-dimensional distribution of CLS-filter in frequency domain

图7 a和图7b分别为直接采用逆滤波器反演与采用约束最小二乘方滤波反演的计算结果。可见直接采用逆滤波计算的结果虽然可见清晰的电荷分布轮廓，但背景噪声残留较多。过多的噪声残留可能在实际应用中覆盖部分有效信号，从而影响对测量结果的判断。而采用约束最小二乘方滤波的反演结果与实际表面电荷密度分布基本一致，且背景噪声被有效抑制，视野内无显著噪点。相比实际表面电荷密度分布，反演图像仅在电荷密度值突变的字母边缘处稍显模糊。其原因在于，此时CLS-filter为一低通滤波器，高频分量在计算过程中会被衰减，而实际电荷分布测量结果往往是渐变的，很少出现图5a所显示的电荷密度分布突变的极端情况[16,18]。

图7 表面电荷反演结果Fig.7 Inversion result of surface charge distribution based on different method

2.4 精度分析

本文在2.3节算例的基础上叠加不同大小的高斯噪声来测试不同噪声等级下CLS-filter算法的反演效果，并采用信噪比（SNR）与峰值方均误差（PMSE）的二次方根来评估算法的反演精度。其计算方法为[11]

图8 所示为不同噪声叠加下的表面电荷反演结果，可见复原图像均能与实际表面电荷密度分布良好吻合，且外加噪声等级在0.5%以下时背景噪声抑制效果优异，视野内几乎观察不到显著噪点。根据上述算例评估本算法的反演精度，不同噪声下反演电荷的信噪比与峰值方均误差见表1。当噪声等级为0.1%时，反演算法的信噪比可达42.3 dB，其峰值方均误差PMSE的平方根仅为0.78%。随噪声等级的提升，反演精度下降，但在2%噪声干扰下其SNR仍有25.3dB。可以预见，若原始表面电荷分布不发生本文所设置的突变效果，则算法的精度会更高，因此在实际测量中本算法将对表面电荷分布图谱有更好的复原效果。

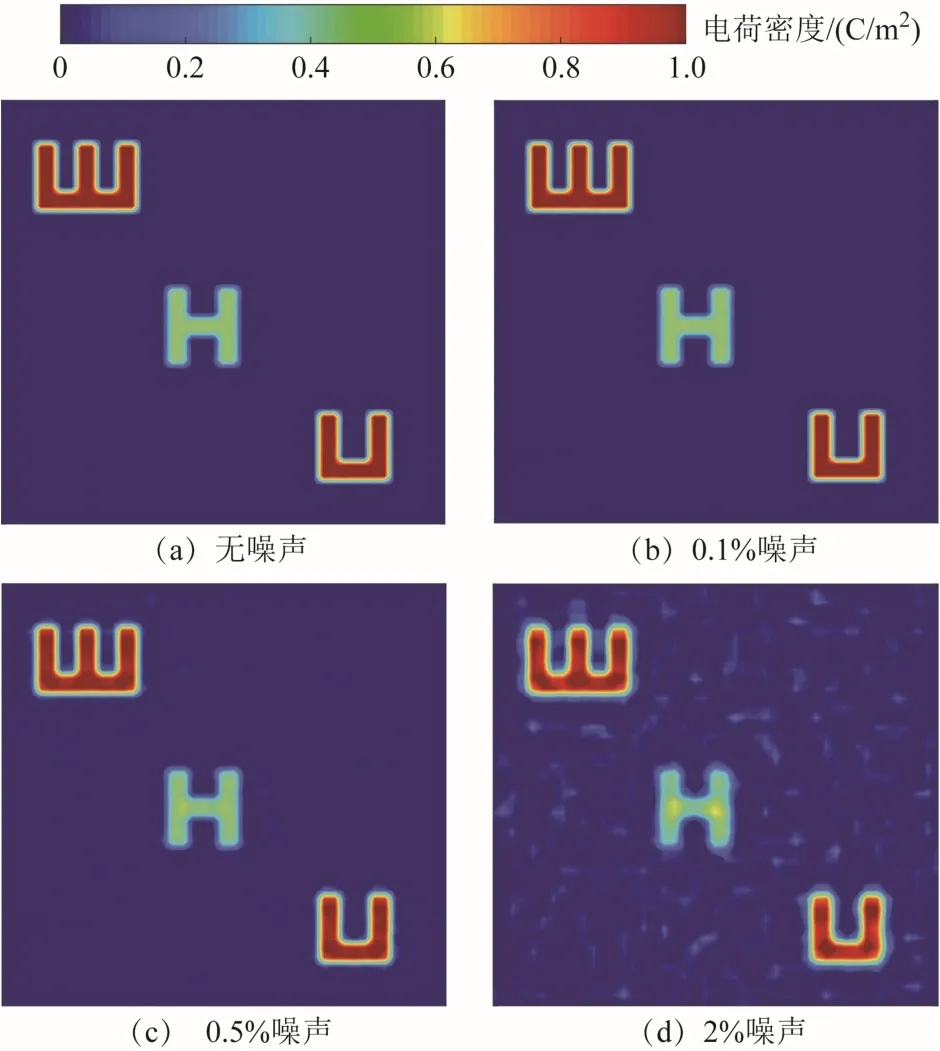
图8 不同噪声叠加下的CLS-filter反演结果Fig.8 Inversion results of different Gaussian noise superimposition based on CLS-filter

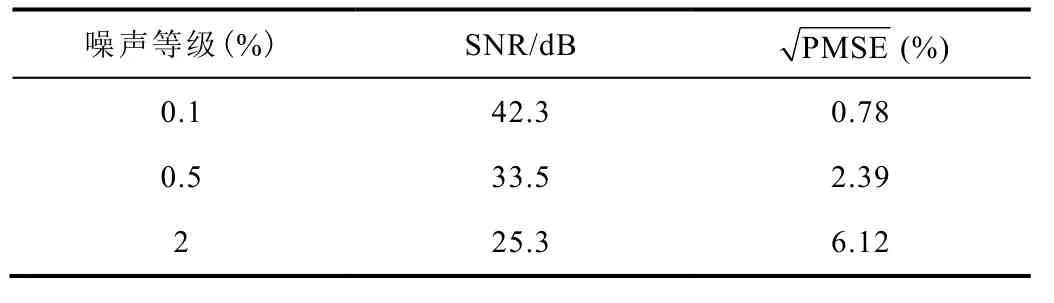
表1 不同噪声下反演电荷的信噪比与峰值均方误差Tab.1 SNR and PMSE for the inversed charge distribution with different noise level

3 各反演算法对比

根据反演计算中是否需要通过多次电场数值计算来求解电位-电荷转换矩阵及其逆矩阵，本节将电荷反演算法分为两类。A类：不需要求取；B类：需要求取。并分别选择这两类算法中的一种为代表来与本文所述CLS-Filter算法进行对比。

3.1 A类算法：维纳滤波法

维纳滤波法作为同样是利用频率域滤波实现表面电荷反演的算法，近年来广受关注。维纳滤波器的频域表达式[25]为

式中，Sn(u,v)为噪声功率谱；Sf(u,v)为未退化图像的功率谱。

在基于维纳滤波的反演计算过程中，为获取最佳的图像复原结果，需要求取系统的噪声功率谱与未退化图像的功率谱，但这两个量在实际中很难获取，通常令Sn(u,v)/Sf(u,v)为一固定常数K，在计算过程中交互式地调整K值的大小，来获取视觉上较好的图像复原效果。但功率谱比值的常数估计并不总是一个适合的解决方案，这将给计算结果引入较多主观因素，在实际操作中难以控制反演精度且手工调试滤波系数将大大降低计算效率。相对而言，本文所述约束最小二乘方滤波器的滤波系数求取仅需噪声方差与均值的知识，这些参数往往可以通过给定的退化图像计算出来[25]。因此，在计算效率与运算精度的把控方面，CLS-filter要优于维纳滤波器。

图9 和表2所示为不同等级噪声叠加下的维纳滤波反演结果与精度计算。对比相同仿真算例下维纳滤波法与CLS-filter法两种反演算法的结果可知：对于低噪声的情况，两种算法都能较好地复原电荷分布图谱。在噪声等级小于0.5%范围内，信噪比均大于30dB，峰值方均误差的平方根小于3%。而对于高噪声的情况，基于CLS-filter的反演算法所得结果则优于维纳滤波法，具体表现为CLS-filter法在视觉上具备更好的背景噪点抑制效果，且其计算结果具备更高的信噪比与更小的峰值方均误差。

图9 不同噪声叠加下的维纳滤波反演结果Fig.9 Inversion result of different Gaussian noise superimposition based on Wiener filter

表2 不同噪声下维纳滤波法反演电荷的信噪比与峰值方均误差Tab.2 SNR and PMSE for the inversed charge distribution with different noise level based on Wiener filter

3.2 B类算法：模拟电荷法

模拟电荷法作为一种常规的反演算法，其适用范围包括平移不变系统与平移改变系统。该方法的实现需要经过两个过程[29-30]：①N×N次电场数值计算求取转换矩阵H；②求H的逆矩阵并代入式（3）求解电荷密度分布。

本次模拟所用计算机CPU：i7-8700，内存64G，静电场计算在COMSOL中完成，建模所用几何尺寸与测量网格同2.3节所述完全一致。考虑到该算法的计算精度受网格剖分影响较大，本节控制其网格密集度与A类算法的矩阵维度保持一致。具体地，如图10a和图10b所示，试样表面每一行剖分为45个区域，一共45行。每次计算时，令其中一个区域表面电荷密度为1C/m2，其余区域电荷密度为零。依次进行2 025次(45×45)循环计算来获取系统转换矩阵。单次计算耗时约8s，求取该网格下的转换矩阵共计耗时约4 h 30 min。相比只需通过系统冲击响应来获取转换矩阵频域表达式的A类算法而言，模拟电荷法在绝缘子形状非旋转对称的情形中计算量过大，尤其是在网格剖分密集时的计算效率较低。

图10 模拟电荷法计算模型Fig.10 Calculation result of simulated charge method

针对相同算例，图11与表3所示为不同等级噪声叠加下的模拟电荷法反演结果与精度计算。可见模拟电荷法对干扰噪声的抑制作用弱于维纳滤波法与CLS-Filter法，宏观表现为反演所得电荷分布图谱的背景噪点较多。在噪声等级为0.1%的低干扰条件下信噪比仅为36.9dB，但从整体结果来看，仍能较好地复原实际电荷分布。而当噪声等级上升至2%时，视野中残留背景噪点显著增多，有淹没目标电荷密度分布的趋势，且伴有明显的电荷分布图谱的形状畸变。因此，该算法抗噪声干扰能力弱，在外加干扰噪声下的计算精度较低。且对于绝缘形状非旋转对称的试样而言，在网格密集的计算条件下会大大增加计算量，降低计算效率。

图11 不同噪声叠加下的模拟电荷法反演结果Fig.11 Inversion result of different Gaussian noise superimposition based on simulated charge method

表3 不同噪声下维纳滤波法反演电荷的信噪比与峰值方均误差Tab.3 SNR and PMSE for the inversed charge distribution with different noise level based on Wiener filter

3.3 偏差度分析

为进一步研究各算法对图像中目标信号的复原能力，本节提取了上述三种算法所得结果中的数据点，来评估反演结果与原始“WHU”字母处电荷密度值之间的偏差，进而在电荷量级上分析不同等级噪声干扰下各算法的图像复原效果。

这里引入偏差系数ξ定义为

式中，δ为“WHU”各字母处原始表面电荷密度分布；ˆδ为反演所得各字母处表面电荷密度平均值。

不同噪声叠加下的各算法反演结果的偏差度如图12所示，在噪声等级为0.1%的低干扰条件下各算法所得结果与实际电荷密度相比偏差度较小。其中，本文所述CLS-filter算法偏差度最低，平均偏差系数不足1%。随着干扰等级的提升，各算法所得结果的偏差度均有一定程度的上升，在不超过0.5%的噪声条件下，CLS-filter法的计算结果略优于维纳滤波法，二者平均偏差系数分别为2.732%与3.065%。相对而言，模拟电荷法的计算偏差显著升高，最大偏差系数上升至6.842%。随着噪声等级进一步上升至2%，各算法偏差度显著提升，但CLF-filter法仍保持着三者中最小偏差系数。需要注意的是，外部过高的噪声干扰可能会淹没目标信号，因此频率域滤波算法在复原图像轮廓的过程中将不可避免地滤除部分目标信号，进而导致复原图谱中的电荷密度低于实际电荷密度，这也是高噪声条件下反演偏差系数显著提升的主要原因。

图12 不同噪声叠加下的各算法反演结果的偏差度Fig.12 Deviation level of inversion results under different Gaussian noise superimposition

4 实验验证

为验证本算法的有效性，本文搭建了基于针-板电极结构的测量平台，通过电晕放电对绝缘子表面进行充电并开展实验验证，基于针-板电极的绝缘子表面电荷测量平台如图13所示。

图13 基于针-板电极的绝缘子表面电荷测量平台Fig.13 Measuring platform of surface charge distribution based on needle-plate electrode

所用试样为3mm厚的圆形环氧树脂板，设置针尖间距试样表面3mm，静电探头距试样表面2mm。利用直流-8kV加压2min后测量其表面电位分布，详细测量过程参见前文的研究[31]，测量条件与2.3节中的仿真算例保持一致，即：探头扫描区域大小为45mm×45mm，每个测量点间隔1mm。在获取表面电位分布的基础上，利用不同反演算法求取试样表面电荷密度分布，进一步采用粉尘图法检验反演结果与实际电荷分布图谱的吻合度。

粉尘图法实验过程示意图如图14所示，粉尘图法采用球形黑色碳粉，平均粒径10μm，粉尘容器的封口处为孔径800目的筛网。当静电探头测量完毕后，从试样上方喷洒粉尘，粉尘容器中孔径大于800目的杂质颗粒被筛网有效隔绝。由于粉尘颗粒细，质量轻，将在试样周围的空间中呈现近似悬浮状态。进而在一段时间后，受绝缘子表面电荷自建电场作用，自由附着于绝缘子表面，形成表面电荷分布轮廓。通过让粉尘悬浮于周围空气中并自由吸附至绝缘子表面可在一定程度上减小粉尘喷洒过程对原有电荷分布的影响，从而尽可能地提升粉尘图像准确度[32]。

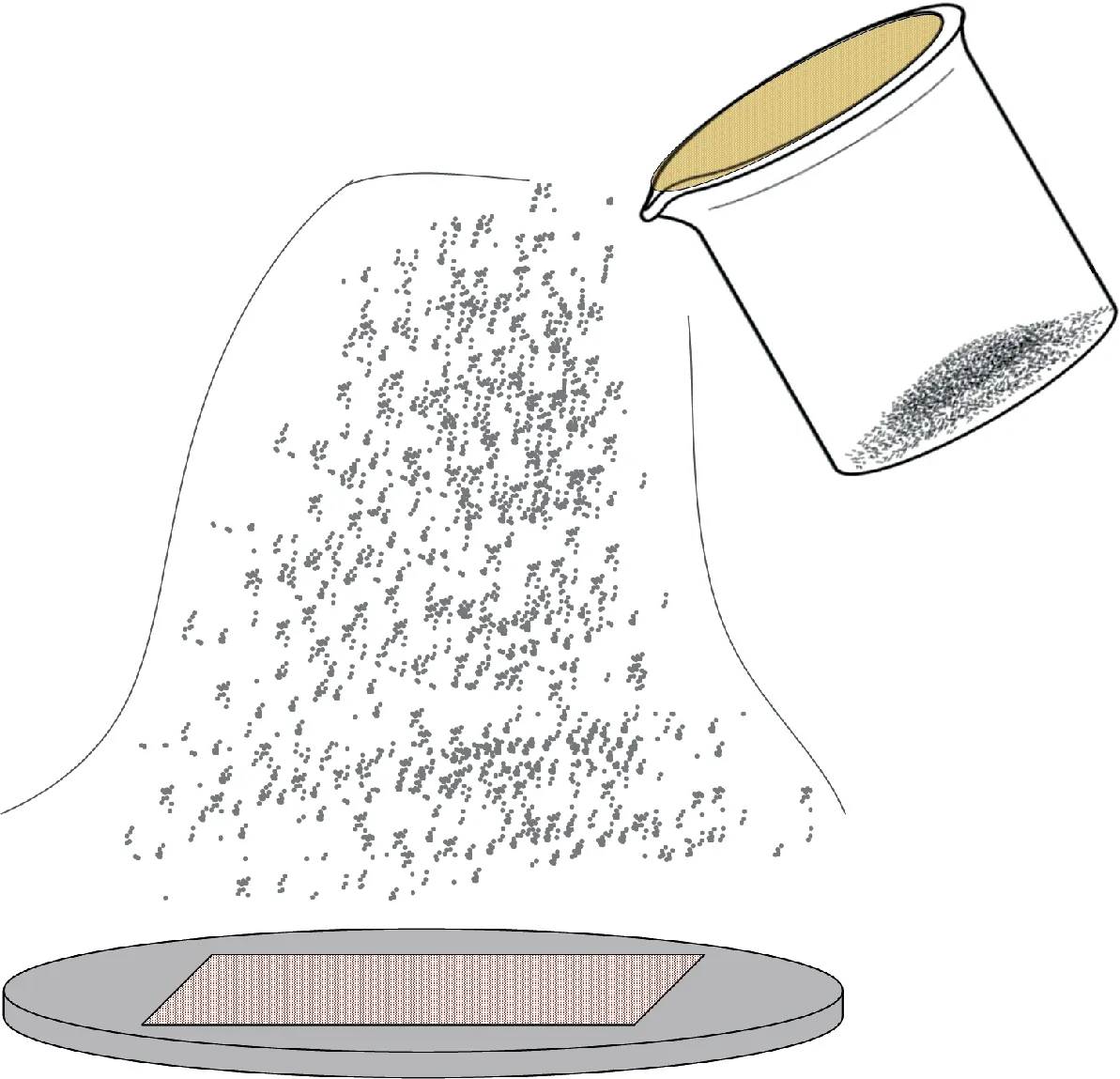
图14 粉尘图法实验过程示意图Fig.14 Schematic diagram of dust figure method

表面电位测量值如图15所示，在针-板电极结构下绝缘子表面电位分布主要积聚在试样中央，近似呈椭圆形分布。相比粉尘图的结果而言，表面电位分布图谱边缘存在轻微的锯齿状斑纹，这意味着表面电位分布与电荷密度分布图谱存在一定差异性。因此在实际工程中，不可直接采用电位分布来代替电荷密度分布。

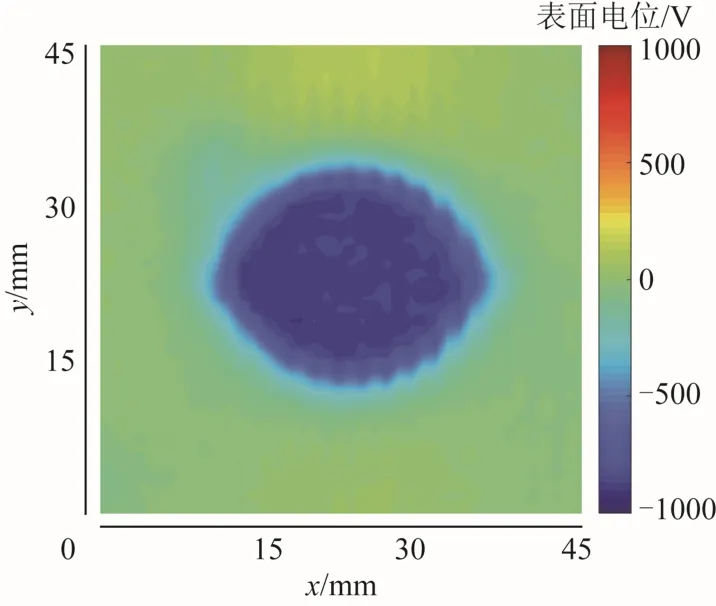
图15 表面电位测量值Fig.15 Calculated results of surface charge distribution under different inversion algorithm

图16 所示为分别采用模拟电荷法、维纳滤波法、约束最小二乘方滤波法、粉尘图法所得表面电荷分布。可见，模拟电荷法所得结果与粉尘图所示相差较大，电荷斑边缘处有显著的波动，且图像背景噪点较多。而维纳滤波法与约束最小二乘方滤波法则有更好的背景噪声抑制效果，且从图像复原效果来看，本文所述约束最小二乘方滤波法所得结果与粉尘图所示电荷分布图谱更为吻合。

图16 不同方法所得表面电荷分布Fig.16 Surface charge distribution based on different method

进一步地，本文提取了图16中各算法所得反演结果，针对其电荷密度进行定量对比。图17所示为不同算法所得结果沿测量区域中心线的表面电荷密度分布。可见三种算法均能复原出针-板电极加压下的典型“火山口”状电荷分布[33-35]，但模拟电荷法下的沿线电荷分布波动显著高于CLS-filter法与维纳滤波法。进一步印证了其抗干扰能力较弱的缺点，所得反演结果因背景噪声的存在而产生较大波动。相对而言，另外两种算法的沿线电荷分布曲线则相对平滑，相较模拟电荷法有着更好的噪声抑制效果。

图17 沿测量区域中线的表面电荷密度分布Fig.17 Surface charge distribution along the center line of measuring area

图18 所示为三种反演结果所得表面电荷密度的最大值与平均值。其中，模拟电荷法所得结果最大值与平均值分别为14.98pC/mm2与6.34pC/mm2，结合图17分析可知，该方法由于抗干扰能力较弱，在反演结果中将残留较多干扰信号，该信号与同符号的原始信号叠加是导致其计算所得电荷密度值高于其余两种算法的主要原因。而CLS-filter法与维纳滤波法所得电荷密度值相近，但维纳滤波法的结果更小，分别为：最大12.67pC/mm2，平均5.42pC/mm2。结合本文第3节的分析可知，维纳滤波法虽能有效抑制噪声干扰，但其理论计算精度相比CLS-filter法更低。另外，在图像处理领域已经被证明，维纳滤波器对噪声的抑制能力弱于约束最小二乘方滤波器，且利用维纳滤波器的图像复原过程是建立在最小化统计准则的基础之上，因此其计算结果在平均意义上是最优的；而约束最小二乘方滤波器则对其作用的每幅图像都能产生最优结果[25]。在相同干扰条件下，为了在视觉上获取同级别的背景噪点抑制效果，必须进一步增大维纳滤波系数以增强其去噪能力，这将不可避免地衰减目标信号大小，使反演所得电荷密度值（目标信号）偏小。综上所述，本文所述CLS-filter算法相比前两者具备更好的准确性与抗干扰能力，图像复原精度更高。