面向元动作的机械传动系统可靠性分配方法

陈一凡 张根保,3 冉 琰 李宇龙 庾 辉

1.重庆大学机械工程学院，重庆，400044 2.重庆大学机械传动国家重点实验室，重庆，400044 3.重庆文理学院机械工程学院，重庆，402160

0 引言

可靠性分配是产品早期设计和开发阶段的关键步骤之一,其目的是将产品整机的可靠性指标分配给每个基本单元，以确保组成整机的各基本单元的可靠性满足可靠性设计要求[1-3]。目前，传统的可靠性分配方法主要侧重于两个方面：一是基于模糊理论的可靠性分配[4-5]；二是基于优化算法的可靠性优化设计[6-8]。虽然这些可靠性分配技术得到了广泛的应用，但是，前者方法主要依赖专家评分，主观性较强，而后者方法忽略了机械系统的结构特性，此外，它们有一个共性问题，即它们都沿袭了电子产品的可靠性分配模式，因此，为了提高机械系统的可靠性，研究一种适用于机械系统的可靠性分配方法迫在眉睫。

近几年来，国内外学者对机械系统的可靠性分配工作进行了相关研究。张强等[9]考虑机械系统分配中的多层影响因素，建立了两层因素的可靠性分配模型。王昊等[10]提出一种考虑子系统故障相关性的多因素可靠性分配方法。张义民等[11]通过引入模糊数学理论，提出了一种基于用户反馈的数控机床故障信息的可靠性模糊分配方法。张根保等[12]引入“任务”概念，提出了一种基于“任务”的数控机床模糊可靠性分配方法。YU等[13]提出了一种考虑失效影响和可靠性成本的综合模糊分配方法，随后，他们在目标可行性(feasibility-of-objectives，FOO)方法的基础上，提出了一种考虑依赖因子的分配方法[14]。CHENG等[15]将模糊分配与最大熵有序加权平均(ME-OWA)方法相结合并将其应用于数控机床的子系统，提高了分配的灵活性。ZHANG等[16]提出了一种综合考虑运动机构的组成和三类失效模式的可靠性分配方法，并成功将其应用于飞机齿轮门锁机构。LIU等[6]为了找到全局最优的可靠性指标，提出了一种基于多学科设计优化的可靠性分配建模求解方法。

然而，现阶段机械系统的可靠性分配研究还存在以下关键问题需要进一步解决：①现有的可靠性分配仍然按照“系统-部件-零件”的路径分解，而实际的机械系统为由运动单元组成的传动链，传统的自顶向下的分解会导致分配任务越来越繁琐，分配效率较低[14,17]；②运动单元的可靠性决定了整机系统的可靠性，在不确定性条件下，各运动单元对系统可靠性的影响存在一定的差异，这一点在传统的可靠性分配中并未体现。

针对以上问题，本文提出了一种基于元动作及其灵敏度的机械传动系统可靠性分配方法。从运动和传动的角度，将机械系统分解为最基本的运动单元(即元动作)，并将其作为可靠性分配的最小粒度，然后，考虑到处于传动系统结构不同位置的元动作对整个系统可靠性的影响存在很大的差异，本文引入灵敏度指标对其进行不确定性量化。该方法能够将难以定量评估的问题进行量化，以灵敏度指标作为可靠性分配的有力依据，从而为可靠性分配工作提供新的思路。

1 可靠性分配模型的建立

针对传统的机械传动系统可靠性分配的不足，本文提出一种基于元动作及其灵敏度的机械传动系统可靠性分配方法，其分配框架如图1所示。首先，采用“功能-运动-动作(function-motion-action，FMA)”的分解方法[17-19]对机械系统进行分解得到元动作集合，并将其作为分配的最小粒度;然后，利用拉丁超立方体抽样(Latin hypercube sampling，LHS)方法计算低阶逼近(low-rank approximations，LRA)元模型的系数，并通过后处理LRA的系数求解各元动作在传动链中的灵敏度；最后，基于获得的元动作灵敏度计算结果识别出系统的关键元动作，并将传动系统的整机可靠性指标分配到各元动作。虽然基于LRA的Sobol’方法在其他领域已有相关研究[20]，但是将其应用于可靠性分配领域还未见相关报道。

图1 可靠性分配框架Fig.1 The reliability allocation framework

1.1 基于FMA方法的机械系统分解

注：不带箭头的实线连接表示组成关系；带有箭头的实线连接表示映射关系；带有箭头的虚线连接表示传动关系图2 FMA分解示意图Fig.2 Diagram of FMA decomposition

功能分解是将产品功能分解为相应的子系统或部件的运动。传统的功能分解方法[21-22]的最后节点处是针对零件而言的，如果分解对象为复杂的大型机电产品，则不利于产品的性能分析。FMA方法是从运动的角度将产品功能分解到最基本的运动单元，即元动作,FMA分解过程如图2所示。从图2中可以看出，元动作层实际上是由一条传动链组成的，只要确保各元动作能够正常运行，那么就能实现产品所需的功能，这与可靠性分配的目的是一致的。因此，功能分解的目的是明确各元动作的详细可靠性输入值，以进一步合理设计各元动作。

由于数控机床是一个串联结构，各功能的正常输出取决于所有元动作的正常工作，因此，可以将它们视为一个串联系统。根据可靠性理论，元动作的可靠性与系统的可靠性关系表示为

(1)

式中，Ri为元动作Ai的可靠度；RS为传动系统的可靠度；n为元动作数目。

随着时间的推移，系统可靠性呈单调递减趋势，这可以理解为系统中某个或多个元动作出现退化，而在这个退化过程中存在不确定性因素，如应力、磨损和员工的操作方式等，这些不确定性因素造成元动作的性能处于一个区间范围，因此，每个元动作可以看成是系统的一个随机变量，则式(1)可以等效为

Y=f(X1,X2,…,Xn)

(2)

将式(1)转换成式(2)的目的是为了后续分析每个随机变量Xi(i=1,2,…,n)对函数Y的灵敏度，即元动作对系统可靠性的影响程度。

1.2 基于LRA的全局灵敏度分析方法

1.2.1全局灵敏度分析

全局灵敏度分析(global sensitivity analysis，GSA)定义为响应模型中输入变量的不确定性对模型输出响应的不确定性的贡献程度。Sobol’方法[23]是工程实际应用中最广泛的GSA方法之一，它可以分析单一输入变量作用或多个输入变量之间相互作用对系统输出的影响。

为不失一般性，设函数f(X)在单位超立方体Ω(n)中，且输入为n维，则Ω(n)可以表示为

Ω(n)={X|0≤Xi≤1;i=1,2,…,n}

(3)

Sobol’法的关键步骤是将函数f(X)进行分解,即

(4)

其中，f0为常数，fi是Xi的函数，fij是Xi和Xj的函数，其余各项对其所包含的每一个因素的积分为0，即

(5)

1≤k≤s

由于函数分解中的所有项之间都为正交，且式(4)的分解存在唯一性，那么所有展开式的和都可以通过积分以递归的方式计算得到，即

(6)

式中,fi表示Xi单独变化对Y的影响(称为Xi的主效应)；fij表示除了i、j各自变化的影响之外，Xi和Xj同时变化对Y的影响；E(·)为期望算子。

对于f2(X)可积函数，可以对函数分解进行平方和积分，进而得到f(X)的总方差，即

(7)

式(7)等式左边为Y的方差，右边为方差项。根据Xi的集合分解式，方差表达式的分解表示为

(8)

(9)

式中，X～i为去除Xi之外的所有变量的集合，即X～i={X1,…,Xi-1,Xi+1,…,Xn}。

因此，一阶Sobol’指标(first-order Sobol’indices，FSI)和总Sobol’指标(total Sobol’indices，TSI)分别表示为

(10)

(11)

FSI反映了单一输入变量Xi的不确定性对输出变量的影响，Si越大，说明该输入变量对系统输出的影响越显著。

TSI用于评估单一输入变量及其与其他输入变量的相互作用对系统输出的共同影响。如果输入变量间相互独立，则FSI值总是小于TSI值；若两者相差较大，则说明输入变量间的相互作用对系统输出的影响更显著。

通常，计算Sobol’法指标的常用方法有两种，即基于蒙特卡罗(Monte Carlo，MC)方法和基于元模型方法。相对来说，元模型(即替代模型)比MC方法计算效率更高，因为它是用统计上的等价模型来代替复杂模型的。常用的元模型有多项式混沌展开(polynomial chaos expansion，PCE)和LRA，鉴于LRA比PCE的计算结果误差更小[24]，本文提出一种基于LRA的灵敏度后处理方法，该方法具有计算效率高、耗时短等优势。

1.2.2基于LRA的全局灵敏度指标计算方法

LRA是元模型中处理高维模型的一种有效方法，其目的是用少量的秩一张量的和来逼近模型的输出响应值，并利用多元基的张量积形式减少未知系数的数目。因此，Sobol’灵敏度指标可以通过后处理LRA的系数来计算得到[20]，多项式基的LRA元模型可以表示为

(12)

因此，基于LRA的Sobol’方法的计算分别取决于以下FSI和TSI的表达式：

(13)

(14)

由于式(13)、式(14)都涉及均值和方差，因此，将模型Y代入LRA元模型中，然后基于LRA系数计算出这些值，则模型输出的均值和方差分别近似为

(15)

(16)

Si表达式中的E[E(Y|Xi)2]可以近似为

(17)

STi表达式中的E[E(Y|X～i)2]可以近似表示为

(18)

对于更高阶指标的表达式也可以根据LRA系数获得。通过利用多项式基的张量积形式可以将未知系数的数量减少一个数量级，进而使用相对较少的秩数以足够的精度逼近响应值。因此，基于LRA的Sobol’方法能够快速计算出灵敏度指标。

1.3 元动作与传动系统的可靠性映射关系分析

为了使整个传动系统可靠性保持相对稳定，应该降低元动作对系统可靠性的灵敏度。以灵敏度指标作为分配权重，将具有较高灵敏度的元动作分配以更高的可靠性。因此，元动作与传动系统可靠性的映射关系表示为

(19)

式中，S′i为元动作的相对权重，记为ωi。

然后，将ωi取反(即1-ωi)，且对其进行归一化处理，从而得到元动作的最终分配权重ω′为

(20)

最后，各元动作分配得到的可靠度为

(21)

2 案例分析

数控机床作为复杂机电产品的经典类型之一，在制造业加工领域扮演着重要的角色，例如汽车、航空工业和船舶工业等。特别是早期的产品设计，将整机或系统的可靠性目标值合理地分配给各运动单元是非常关键的，合理的可靠性分配能提高产品的质量，并进一步提高产品的生产效率。鉴于数控转台是加工中心的一个关键功能部件[17,25]，本文将其作为实际应用案例来验证提出方法的可行性和有效性，数控转台的结构示意图请扫描本文首页二维码查看。根据产品可靠性要求，数控转台的分度回转运动可靠度RS=0.89。

根据数控转台运动特性，利用FMA分解方法将数控转台的分度运动分解为6个元动作[26]，共组成4条传动链，如图3所示。

图3 数控转台FMA分解Fig.3 FMA decomposition of CNC turntable

运用Sobol’法计算全局灵敏度时，需要先给定参数的变化区间及概率分布函数。数控机床常见的可靠性指标主要有可靠度、失效率和平均故障间隔时间(mean time between failure，MTBF)，它们之间往往是同一概念的不同表达形式。为了便于分析，这里使用MTBF作为统计的指标。分析现有少量的数控转台元动作的故障数据发现，大多数元动作的分布类型服从均匀分布。由文献[27]可知，在不确定性因素条件下，如果随机变量的分布不是特别明确，使用均匀分布计算得到的灵敏度结果不会发生显著性影响。此外，均匀分布能够避免工程实际工程中数据量少、无法确定分布的问题，只需要确定各元动作MTBF的最小值和最大值便可进行灵敏度分析。因此，本文选择均匀分布作为元动作的假设分布类型。具体取值情况如表1所示。

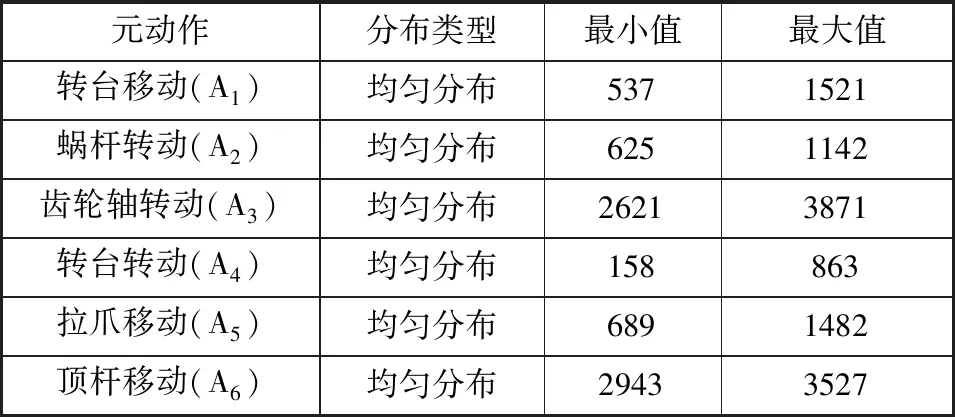
表1 数控转台的元动作分布和取值情况Tab.1 Distribution and value of the meta-actions of the CNC turntable

本文利用UQLab软件[28]建立了基于LRA的Sobol’法的元动作灵敏度模型，其概率输入模型由6个独立的随机变量组成。利用LHS方法对元模型进行随机抽样，并基于200个样本的实验设计创建数控转台可靠性模型的LRA元模型。通过LRA系数快速求解元动作的FSI值和TSI值，并计算出总灵敏度贡献率(TSR)。各元动作对系统可靠性的灵敏度结果如表2所示。

表2 元动作对数控转台可靠性灵敏度结果Tab.2 Reliability sensitivity results of meta-actions to the CNC turntable

由表2可知，灵敏度大小排序依次为SA4、SA1、SA5、SA2、SA3、SA6，其中A4对数控转台的可靠性影响起决定性作用，即是数控转台可靠性的薄弱环节。其原因可解释为：由图3可知，数控转台由4条传动链组成，其中M342是最长的传动链，即由三级元动作组成，从而增大了不确定性因素的影响，这正是在复杂机电产品设计中缩短传动链的主要原因之一。另外，A4位于传动链M342的末端，则上游元动作的性能稳定性输出会对下游造成某种程度的影响[18]，而A4的性能稳定性又直接决定M342是否能够完成指定的运动。因此，为了提高数控转台的可靠性，将A4分配更高的可靠性是有必要的。A1、A4、A5的灵敏度指标为正，且TSR明显比较大，这表明它们的影响很大程度上会降低数控转台的可靠性，在设计环节必须采取适当措施提高其可靠性。另外，可以观察到各个元动作的TSI值与FSI值的差值小于0.1，这说明元动作之间存在较弱的相互作用。为了简化计算过程，这里不考虑相互作用。

根据式(19)～式(21)计算出各元动作的可靠度，如表3所示。

表3 元动作可靠性映射结果Tab.3 Result of reliability mapping of meta-actions

此外，以MC方法模拟计算结果作为基准检验LRA元模型计算结果的准确性和收敛性。图4给出了3个元动作的FSI值和TSI值随MC方法采样次数增加的收敛过程，可以发现采样规模N=100 000时MC方法的计算结果具有较高的准确性。

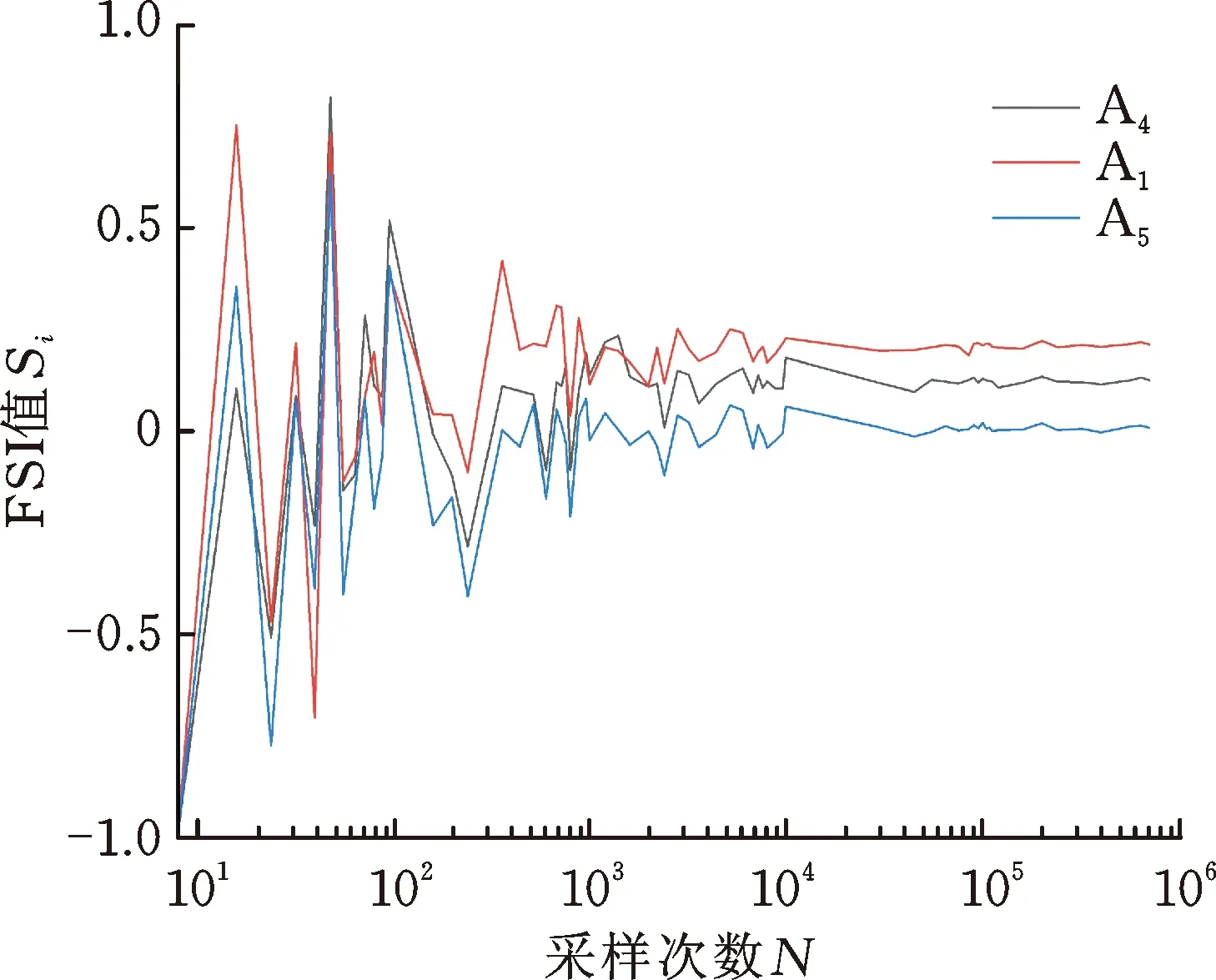
(a)FSI收敛过程

在上述实例基础上，本文将提出的方法与MC方法和PCE方法作对比分析，仿真结果如图5所示。由仿真结果可知，基于LRA的Sobol’法的灵敏度结果与其他两种方法的结果基本是一致的，这说明抽样规模取200时满足收敛条件。由图5可知，基于MC的Sobol’方法的样本规模为100 000，而本文提出的方法在较少的抽样规模(N=200)条件下保证了计算结果的精度，且计算效率更高。

(a)FSI计算结果

由上述分析结果可知，A4、A1和A5是数控转台的关键元动作，根据“木桶效应”，为了提高数控转台的可靠性，应尽可能使灵敏度较大的元动作的可靠性不发生显著变化。因此，提高它们的MTBF，即A4的平均故障间隔时间tMTBFA4=[658,1363]、tMTBFA1=[837,1821]和tMTBFA5=[889,1682]，然后再次对它们的可靠性灵敏度进行分析，其结果如图6所示。

图6 优化前后元动作的灵敏度结果Fig.6 Sensitivity results of meta-actions before and after optimization

由图6可以看出，优化后A4的灵敏度明显比优化前下降了，A1和A5优化前后的灵敏度差异不大。此外，为了检验优化效果，以灵敏度标准差作为波动程度的评价标准，通过计算得到优化前后的标准差分别为0.160和0.096，这就说明优化后的整体灵敏度对系统的影响要小于优化前整体灵敏度对系统的影响。

3 结语

本文利用Sobol’方法分析了元动作对整个传动系统可靠性的影响程度，利用“功能-运动-动作”(FMA)分解得到的元动作作为机械传动系统可靠性分配的最小粒度，这有利于减小可靠性分配的工作量，提高分配效率。同时，以元动作对系统的输出影响作为分配的依据，避免了影响较小的单元分配较高的可靠性设计值，从而使得系统可靠性达到最优。基于低阶逼近(LRA)的Sobol’方法在较少样本条件下能够准确得到元动作对系统可靠性的不确定性输出响应。在此基础上，为提高数控转台的运行稳定性，对关键元动作的可靠性进行了优化，从而为可靠性设计工作提供了指导。

本文从元动作的角度建立了可靠性分配模型，在今后的研究中，为了获取组成机械系统所有零件的可靠性设计值，组成元动作的其他零件(如支撑件、紧固件和传动件等)的可靠性设计值也有待进一步研究。