基于光纤光栅传感器的机床主轴轴承热诱导预紧力研究

2021-09-16卢团良董艳方张亚涛

中国机械工程 2021年17期

卢团良邱明,2 董艳方张亚涛杜辉

1.河南科技大学机电工程学院，洛阳，4710002.机械装备先进制造河南省协同创新中心，洛阳，471000

0 引言

作为数控机床的关键零部件，机床主轴单元，特别是主轴轴承的性能直接影响着机床的加工性能[1]。轴承热诱导预紧力由主轴单元的热膨胀与轴承内部负荷反馈产生，会改变轴承负荷分布，直接决定轴承的运行状态[2]，因此实时监测主轴轴承预紧力，对提高主轴单元服役性能和机床加工精度具有重要意义。

主轴单元产热和传热机理对主轴单元热分析建模至关重要，对此，相关学者开展了大量研究[3-5]，但有关主轴轴承预紧力在线测量系统构建的研究却相对较少。李新宁等[6]构建了预紧力测试电路，利用石英谐振式力敏传感器将力信号以频率的形式输出，经采集卡及相应软件处理，实现轴承预紧力的测量，并通过温度补偿电路补偿石英晶体传感器灵敏度随温度的变化。李荣等[7]构建了弹性预紧轴承组件预紧力测试试验台，利用精密力传感器、位移传感器的监测结果绘制轴承加载刚度曲线，根据曲线的拐点来近似确定弹性预紧轴承组件预紧力。何博侠等[8]发明了一种轴向预紧力传感器，通过主轴左右端盖将轴向预紧力施加到弹性敏感元件，弹性敏感元件因受轴向力而产生应变，利用电阻应变效应测出轴向力的大小。邓四二等[9]在确定的轴承系统中，通过测试拟合预紧力-固有频率-支承跨距关系式，以系统固有频率来判断轴承预紧力大小。吴文武等[10]开发了一种采用小型压电测力传感器进行预紧力实时测量的轴系性能实验平台。王立平等[11]构建了机械主轴系统热分析综合测试实验装置，通过在前后轴套内表面沿轴向粘贴应变片，测量轴套轴向应变情况，间接得出轴承预紧力。胡高峰等[12]利用压电作动器组件作为主轴预紧力的加载装置，通过可滑动套桶设计，结合电作动器、力传感器和位移传感器，建立了在线监测、控制主轴-轴承系统预紧力和预紧位移的高速精密主轴系统。

目前，针对主轴轴承温度场的测量研究，国内外学者还局限于传统的接触式测量或红外线测量方法[13]，轴承预紧力的监测大多是通过电类传感器在试验状态下完成的，不能实现机床加工状态下的测试，难以在线监测轴承热诱导预紧力以反映轴承的真实服役信息。笔者利用光纤光栅(fiber Bragg grating,FBG)“一线多点，无源多场”、体积小、耐腐蚀等测量优势[14]，搭建了主轴轴承预紧力在线测试系统，分析了转速对主轴轴承热诱导预紧力的影响规律，以期为主轴轴承服役状态在线监测及轴承热特性研究提供参考。

1 主轴单元结构

图1为本研究采用的主轴单元结构简图，主要由主轴、角接触球轴承、隔圈、联轴器、轴向加载体以及端盖箱体组成。主轴单元通过联轴器与电主轴相连，通过液压系统加载预紧力，前后端串联安装成对的角接触球轴承SKF7010AC进行支承，且前后端整体呈面对面配置方式，采用定位预紧。轴承结构参数见表1。

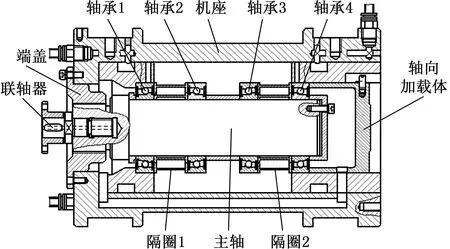
图1 主轴单元结构简图Fig.1 Schematic diagram of the spindle unit structure

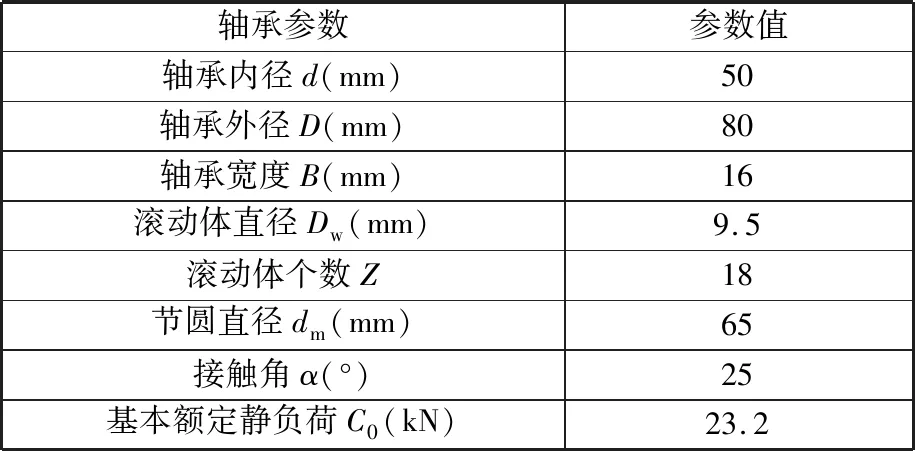
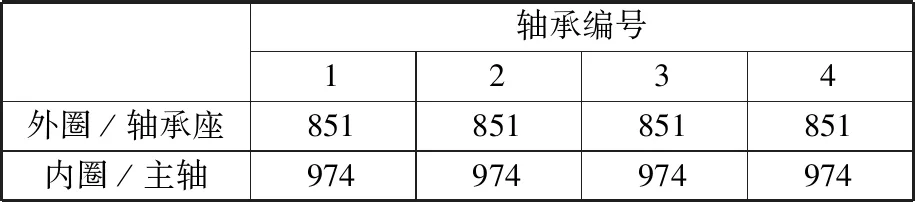
表1 SKF7010AC轴承参数Tab.1 SKF7010AC bearing parameters

2 主轴热源与边界条件

2.1 轴承生热计算

在运行过程中，主轴单元热源主要包括电机发热和轴承摩擦生热。由于本文所测主轴单元与驱动电主轴之间通过联轴器连接，只有极少热量通过联轴器传递至主轴单元，故轴承功率损耗是主轴单元的主要热源。轴承功率损耗可由下式计算[15]：

H=1.047×10-4nM

(1)

式中，H为轴承功率损耗，W；n为主轴转速，r/min；M为轴承总摩擦力矩，N·mm。

轴承总摩擦力矩M由以下三部分组成。

(1)载荷引起的摩擦力矩

M1=f1p1dm

(2)

其中，f1为与轴承类型和载荷有关的系数，对于单列角接触球轴承，f1=0.0013(p0/C0)0.33；p0为轴承当量静载荷，p0=XsFa+YsFr，Fa为轴承所受轴向力，Fr为轴承所受径向力，表2给出了不同接触角单列角接触球轴承的Xs和Ys值；p1为轴承摩擦力矩的计算载荷，p1=Fa-0.1Fr,N。

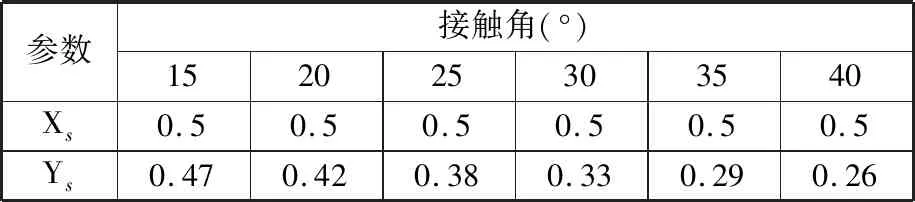
表2 单列角接触球轴承的Xs和Ys值Tab.2 Xs and Ys values of angular contact ball bearings

(2)润滑剂产生的黏滞摩擦力矩

(3)

式中，f0为与轴承类型和润滑方式有关的因数，对于单列脂润滑轴承，f0=2；ν为工作温度下润滑剂的运动黏度，mm2/s，润滑油基础油运动黏度与温度的关系见表3。

表3 润滑脂基础油的运动黏度与温度的关系Tab.3 Viscosity-temperature relationship of grease base oil

(3)单个滚动体自旋滑动引起的摩擦力矩

(4)

式中，μ为接触区各点滑动摩擦因数；Q(k)为滚动体与内外圈的接触载荷(k=i代表内圈，k=o代表外圈)，N；a(k)为滚动体与内外圈接触的椭圆长半轴，mm；Σ(k)为滚动体与内外圈接触椭圆的第二类完全椭圆积分。

轴承内部接触区域滚动体自旋滑动引起的总摩擦力矩

Ms=Z(Ms(i)+Ms(o))

(5)

根据式(1)～式(5)，计算出初始预紧力为350 N时轴承功率损耗与转速之间的关系，见图2。

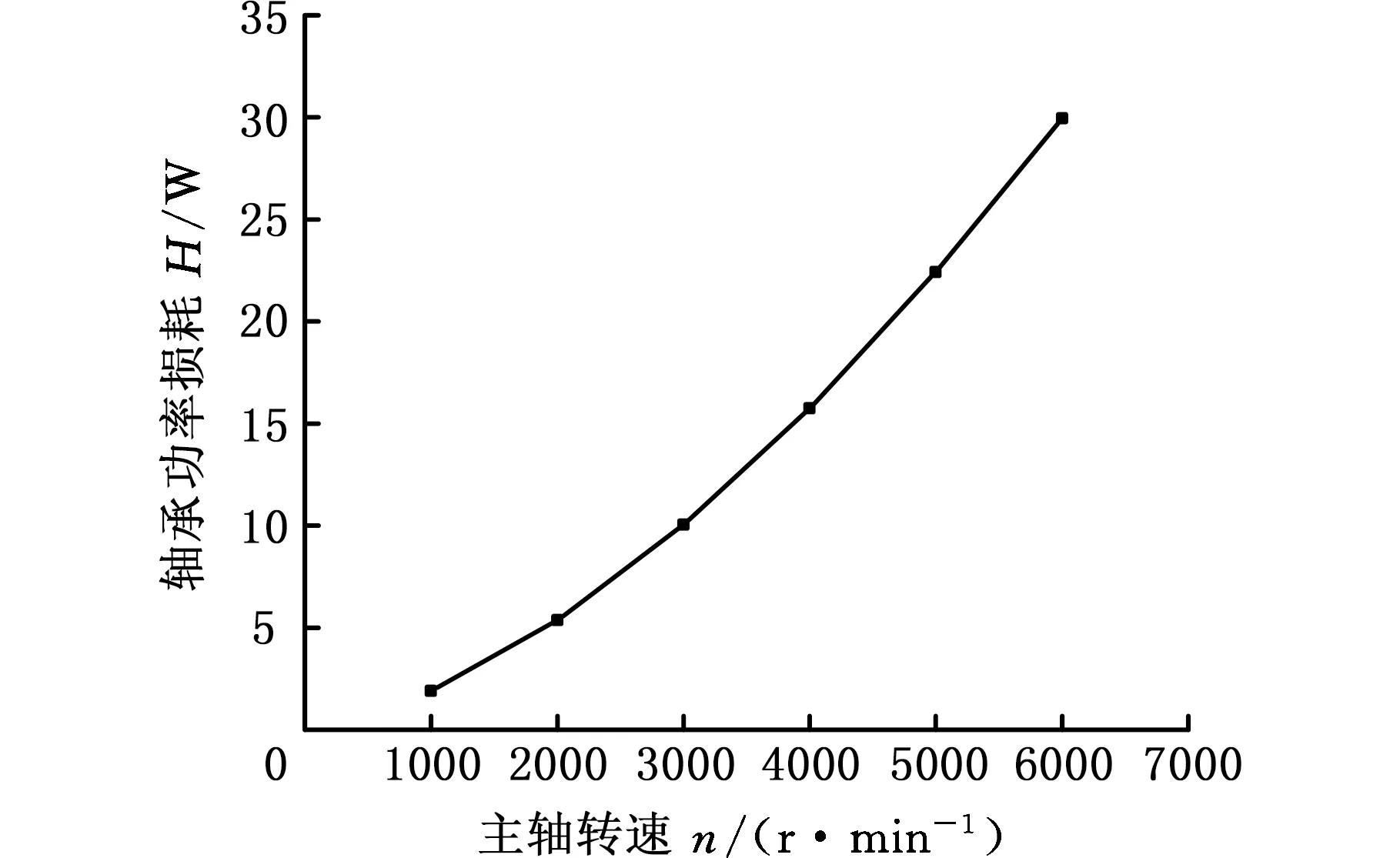
图2 轴承功率损耗与主轴转速关系曲线Fig.2 Relationship between total bearing power loss and spindle speed

2.2 主轴单元边界条件确定

主轴单元各部分传热有热传导、热对流和热辐射三种方式。主轴单元通过热辐射散失的热量较小，在分析时忽略不计，本文主要分析主轴箱内各组件表面的对流传热和轴承内外圈与主轴以及轴承座之间的接触热阻。

2.2.1对流传热系数的计算

在主轴单元内，轴箱等静止零件的表面与空气之间的对流为自然对流，主轴及旋转部件与周围空气间则发生强迫对流。对流传热系数由下式计算：

(6)

式中，Nu为努赛尔数；λair为空气热导率，W/(m·K)。

(1)自然对流。自然对流下努赛尔数为

Nu=C(GrPr)m

(7)

(8)

式中，Gr为格拉晓夫数；Pr为普朗特数，25 ℃干燥空气取0.705；C、m为常数，表4给出了不同流态下的取值；αV为体膨胀系数，K-1；g为重力加速度，m/s2；l为特征尺寸，mm；νair为空气运动黏度，m2/s；ΔT为空气与壁面温差，K。

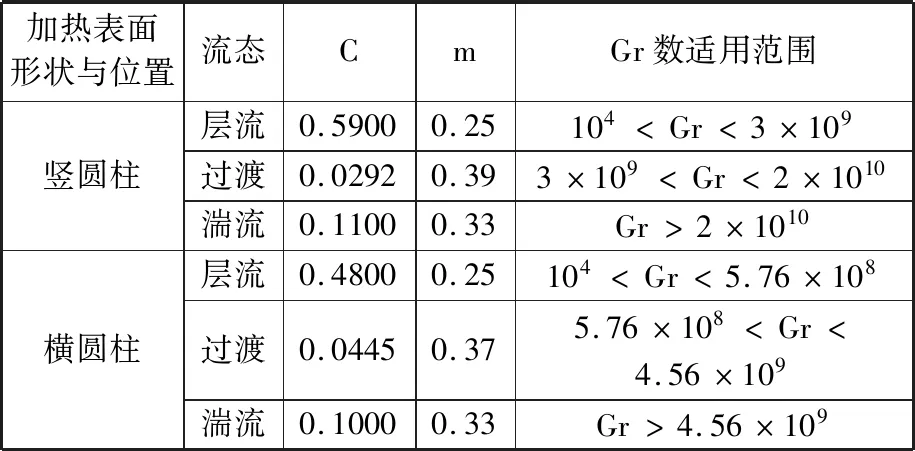
表4 C、m的取值Tab.4 Values of C and m

(2)强迫对流。强迫对流下努赛尔数为

Nu=0.133(Re)2/3(Pr)1/3

(8)

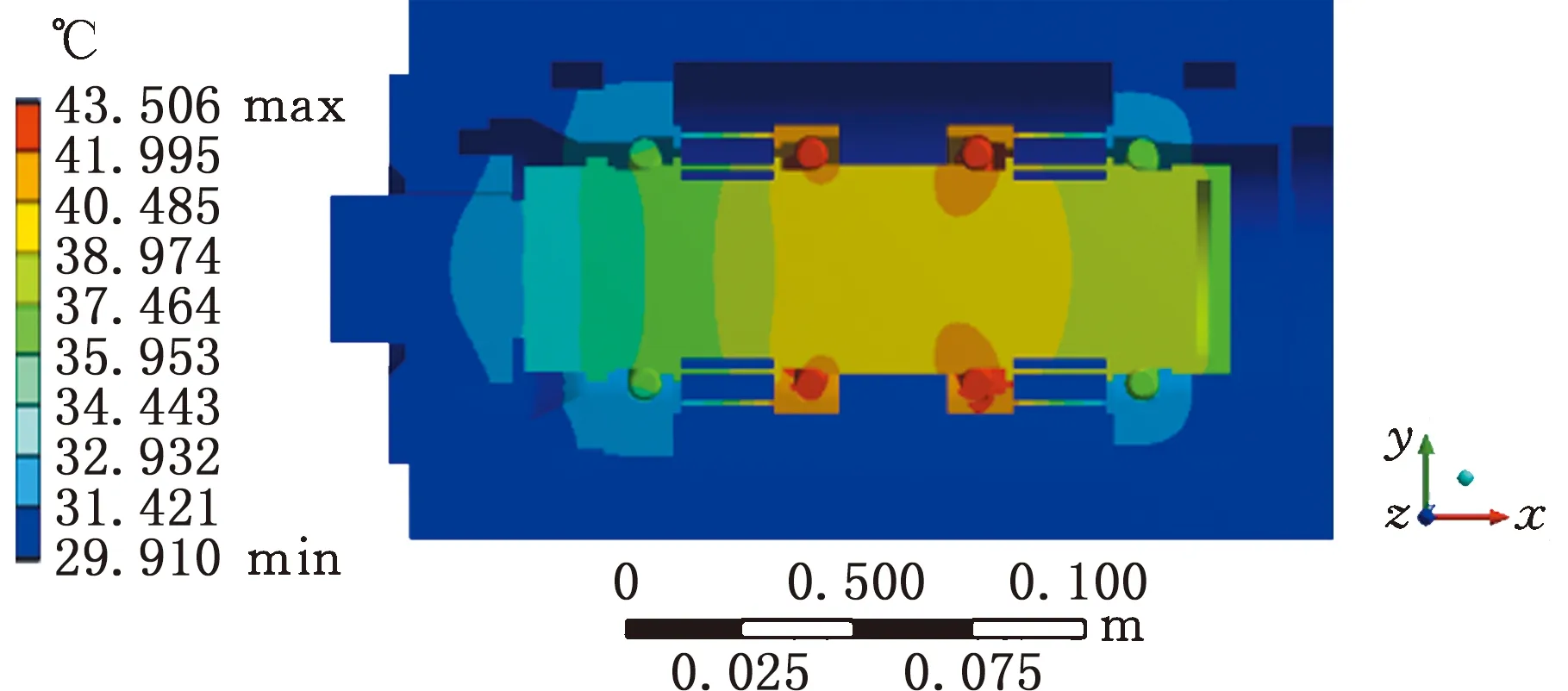
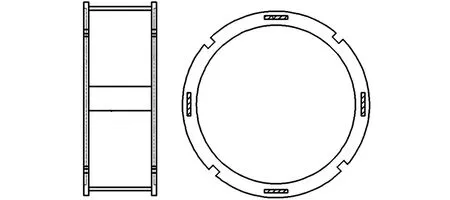
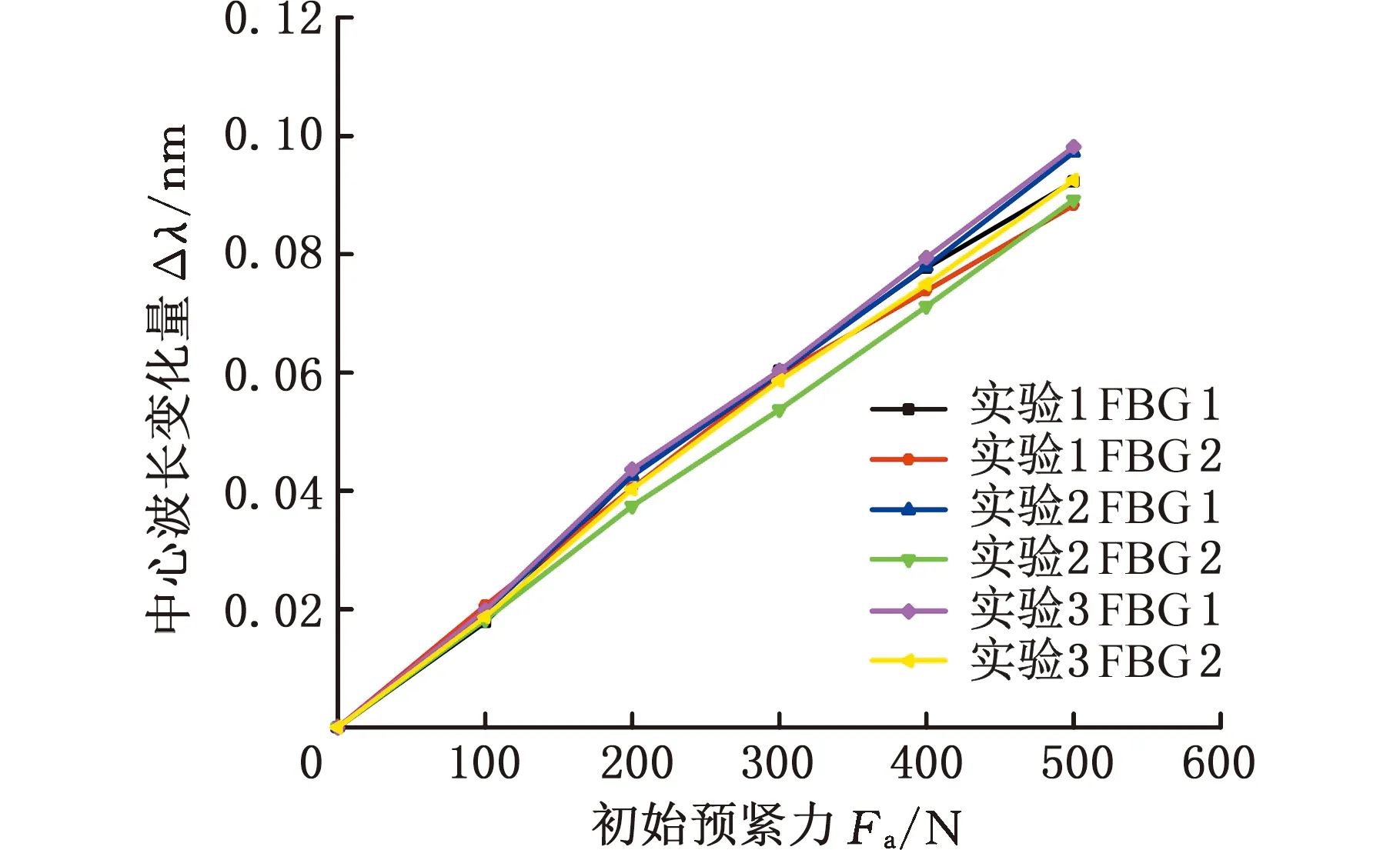
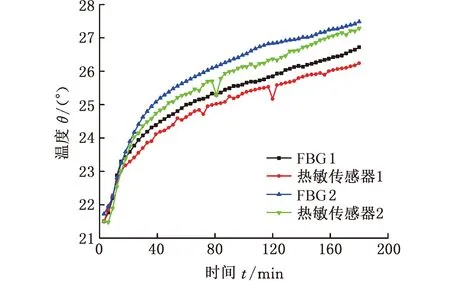
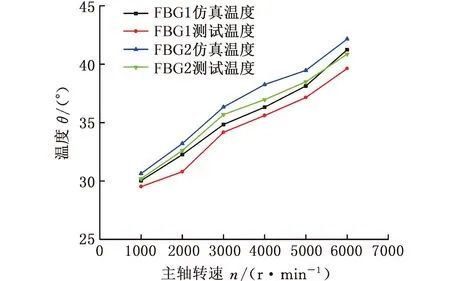
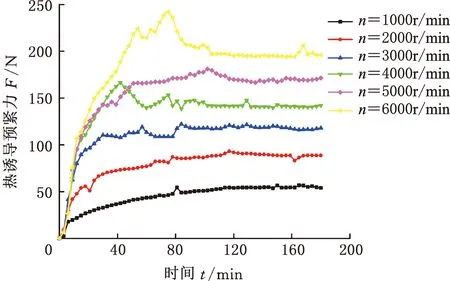
Re<4.3×1050.7

根据式(6)～式(8)计算出强迫对流传热系数与主轴转速和轴径的关系，见图3。周围空气与主轴外壳等固定表面之间的自然对流传热系数为12.3 W/(m2·K)。

图3 主轴表面强迫对流传热系数Fig.3 Forced convection heat transfer coefficient on the main shaft surface

2.2.2接触热阻

轴承内圈与主轴以及轴承外圈与轴承座之间并非完全接触，实际接触仅仅发生在一些离散的面积元上。假设不同工况下，各接触区域接触压力均匀分布，接触热阻可用下式表示[16]：

(9)

式中，λc为接触热导率，W/(m·K)；A为接触区域的名义接触面积，m2。

(1)轴承座与轴承外圈接触热导率λco可表示为

(10)

式中，hr为轴承套圈的厚度，mm；hgap为初始间隙，mm；Tr、Th分别为轴承外圈和轴承座的温度，K；T0为轴座和轴承外圈的初始温度，K；；αr、αh分别为轴承外圈和轴承座的线膨胀系数；rp为轴承座半径，mm；λr为轴承外圈热导率，W/(m·K)。

(2)主轴与轴承内圈接触热导率为

小鸡朝周泽赡跑来，周泽赡亲昵地将小鸡抱上桌子，右手做着圈的动作，小鸡高兴地钻了进去，过一会儿，周泽赡无论如何要让小鸡出来，小鸡恋恋不舍地离开，周泽赡手心沁出的汗，沾湿了羽毛。

(11)

式中，δg为接触表面的间隙，取接触表面粗糙度，mm；A1为实际接触面积，取名义接触面积的0.1%；A2为接触间隙面积，m2；λz为主轴的热导率，W/(m·K)。

根据式(9)～式(11)，计算出主轴单元关键组件接触热导率，如表5所示。

表5 主轴关键组件接触热导率Tab.5 Thermal conductivity of key spindle components W/(m·K)

3 主轴单元热特性仿真分析

3.1 有限元模型

采用SoildWorks进行主轴单元建模，为了方便分析，对模型进行适当简化。将简化模型导入ANSYS中，采用Hex Dominant划分网格，并将轴承、隔圈等关键组件网格细化。主轴单元材料属性见表6。根据试验条件设置仿真温度为25 ℃。

表6 主轴单元材料属性Tab.6 Spindle unit material properties

3.2 主轴单元温度场分析

在轴向力700 N、转速6000 r/min工况下对主轴单元模型进行稳态热分析，得到图4所示的主轴单元稳态温度分布。由图4可以看出，主轴单元内部温度相差较大，中间两套轴承滚动体温度最高达43.5 ℃，两端轴承温度较低，内圈温度略高于外圈温度。这是因为主轴采用脂润滑轴承，滚动体热量散失少；中间两套轴承外圈静止，相较于加载体直接接触的轴承,散热性能差。主轴温度明显高于轴承座，且温度由中部向两端逐渐降低，这是因为轴承外圈与轴承座之间的接触热阻较高。由于后端为轴向力加载端，与前端剧烈强迫对流的工况相比，热量散失少，故前端轴承温度略低于后端轴承温度。

图4 主轴单元温度分布云图Fig.4 Cloud diagram of temperature distribution of the spindle unit

4 基于FBG的主轴轴承预紧力测试系统

4.1 FBG传感器测量原理

光纤光栅的高灵敏性和强适应性，以及易于实现分布测量的特点，为机械系统的多参数分布动态检测提供了新的技术路线。

当外界温度发生变化时，光纤光栅的中心波长变化量[17]可以表示为

ΔλB=KTΔTeλB

KT=αf+ζ

式中，ΔTe为环境温度变化，K；KT为光纤的温度敏感系数，K-1；λB为光纤光栅的中心波长；αf为光纤材料的热膨胀系数，K-1；ζ为光纤材料的热光系数，K-1。

基体材料具有热膨胀效应，其膨胀量完全转移至光纤时，反射波长变化量[17]可以表示为

ΔλB=(1-Pe)ΔελB

式中，Pe为光纤的弹光系数,mm-1；Δε为光纤结构应变，mm。

4.2 预紧力测试系统组成

图5所示为主轴轴承预紧力测试系统装置的布置方案。在前后端串联轴承之间安装如图6a所示的轴承隔圈，在施加轴向力(此处即初始预紧力)Fa之后，主轴前端轴承预紧，主轴向后移动，进而预紧后端轴承。光纤光栅在轴向预紧力和温升作用下波长发生改变，从而可通过解调仪和电脑实时在线监测轴承承受轴向预紧力的变化量，实现轴承热诱导预紧力测试。

图5 预紧力测试系统示意图Fig.5 Schematic diagram of preload test system

4.3 粘贴式FBG温度补偿方法

由于光纤光栅对温度、应变同时敏感，故在测量初始预紧力及单元组件热膨胀引起的轴向应变时需排除环境温度变化带来的影响。

采用图6b所示粘贴方式进行环境温度补偿。轴向粘贴光纤光栅FBG1，在初始预紧力和主轴单元组件热膨胀产生的热诱导预紧力作用下，悬臂梁产生轴向应变，加上环境温度变化的影响，导致中心波长发生变化，中心波长变化量

(12)

式中，λB1为FBG1中心波长；E为隔圈材料弹性模量；wb为悬臂梁宽度;hb为悬臂梁厚度。

(a)隔圈结构示意图

垂直方向粘贴光纤光栅FBG2，在悬臂梁轴向受压缩的同时垂直轴向方向也产生应变，加上环境温度变化，FBG2中心波长变化量ΔλB2可以表示为

(13)

式中，λB2为FBG2中心波长；μc为隔圈材料泊松比。

FBG1与FBG2紧邻，故认为环境温度相同，利用式(12)和式(13)可消除环境温度变化ΔTe对光纤中心波长的影响，即通过FBG2的采集信号补偿环境温度对FBG1的影响。

4.4 传感器标定

考虑到传感器基体对光纤光栅灵敏度的影响，在静止状态下，对主轴单元施加轴向力进行传感器标定。实验分三组进行，实验结果如图7所示。从图7中可以看出，布设的光纤光栅与预紧力变化之间有良好的线性关系，在预紧力为300 N时，测试最大偏差为12.4 N，相对误差4.13%，满足轴承预紧力测量精度的要求。

图7 光纤光栅传感器标定结果Fig.7 Calibration results of FBG sensors

5 主轴轴承热诱导预紧力分析

5.1 热诱导预紧力测量实验系统

图8所示为主轴轴承预紧力测量实验装置，主要包括驱动装置、联轴器、主轴箱、主轴、测试轴承、径向加载装置、轴向加载装置、FBG传感器、热敏传感器、FBG解调仪和数据采集装置等。

图8 轴承热特性实验装置Fig.8 Bearing thermal characteristics experimental device

5.2 与接触式热敏传感器对比实验

在轴承初始预紧力为350 N工况下，主轴以5000 r/min转速运转，通过FBG传感器和接触式热敏传感器测得机床主轴轴承温度特性曲线如图9所示。FBG1测得温度与接触式热敏传感器1测得温度非常吻合，FBG2和热敏传感器2的测定结果亦如此，但FBG传感器的温度曲线比热敏传感器的温度曲线更平滑，这表明FBG传感器的可靠性和抗干扰性更高。热敏传感器1测得的温度略低于热敏传感器2测得的温度，这主要是受基体热膨胀的影响。该实验表明，FBG传感器可以很好地在线测量机床轴承性能参数。

图9 FBG传感器与热敏传感器温度曲线Fig.9 Temperature curve of FBG sensor and thermal sensor

5.3 与仿真结果对比

轴向力为700 N工况下，前后端轴承稳态温度与转速的关系如图10所示。可以看出，轴承温度随着主轴转速的增大而升高，转速对温度的影响基本呈线性。主轴转速升高，滚动体与轴承内外圈摩擦加剧，导致摩擦热迅速增加，进而直接影响轴承的温度。虽然主轴转速升高也引起主轴单元部件的对流换热能力增强，但它对轴承温度的影响远远小于摩擦热对轴承温度的影响，最终导致轴承温度随转速升高而增大。在转速由2000 r/min增大到3000 r/min时，轴承温度变化最大。这是由于转速低时，由载荷引起的摩擦力矩是影响轴承产热的主要因素；随转速升高，润滑剂黏性引起的摩擦力矩和滚动体自旋滑动对轴承产热影响变大，成为主要产热因素。由于驱动端比加载端的散热面积大，故隔圈1的温度略低于隔圈2的温度。

图10 不同转速下轴承稳态温度曲线Fig.10 Steady-state temperature curve of the bearing at different speeds

对比仿真结果与实验结果可知，仿真温度与测试温度最大偏差不超过1.5 ℃，主轴单元仿真稳态温度与实验结果基本吻合，相对误差控制在5%以内，证明了机床主轴单元热仿真模型的准确性。

5.4 预紧力测量结果分析

图11所示为FBG传感器实验中不同转速下前后端轴承热诱导预紧力随时间变化曲线，可以看出，轴承热诱导预紧力在初期迅速增大，随着时间的推移，预紧力上增大度减小，最后趋于稳定。特别是在转速大于4000 r/min后，轴承瞬态热诱导预紧力远大于稳定时的预紧力，这是由于随着主轴转速的升高，轴承产热量大幅增加。主轴启动前期，轴承处热能未能及时传递出去，温度迅速上升，轴承内外圈沟道以及隔圈在轴向产生热膨胀引起预紧力急剧增大。之后随着热传导和对流的进行，主轴和轴承座温升速度减缓，轴承热诱导预紧力也有所减小，最后达到稳定状态。随着转速增大，主轴产热的增加，主轴单元热变形程度增加，最终表现为轴承热诱导预紧力的增大。