基于改进3D-R树的流固耦合模拟网格插值研究
2021-09-16王昭顺董玲玉吴明宇胡长军
苗 雪,王昭顺,朱 迎,董玲玉,吴明宇,杨 文,胡长军
(1.北京科技大学 计算机与通信工程学院,北京 100083;2.中国原子能科学研究院,北京 102413)
反应堆流固耦合(FSI)过程复杂,涉及多学科、受多方因素影响,其重要特征是研究两相介质间的交互作用,即固体在流体载荷作用下会发生形变或运动,而固体的形变或运动会改变流体载荷的分布和大小[1]。流固耦合模拟计算中,一般采用不同的求解器分别对流体域(FD)和固体域(SD)进行求解计算,所以两者离散后的两套网格在耦合界面上是不匹配的,因此需要采用网格插值技术对两套网格的单元和节点建立对应关系以进行耦合界面上信息的传递[2]。
网格插值整体分为局部和全局插值两类,局部插值是根据一定的匹配准则选取另一套网格在待插值节点附近的一些单元或节点上的载荷进行插值计算,求出待插值节点对应的载荷值;全局插值是在另一套网格所有节点载荷的基础上构造一个整体的载荷与坐标的插值函数,根据此插值函数可直接求得待插值节点对应的载荷值[2-3]。局部插值需对网格进行预先搜索以确定待插值节点附近的网格单元或节点,分为基于节点和基于单元两类插值方式。基于节点的插值有最邻近点插值法(NNI)[4-5]和反距离加权平均法(DWA)[6-8],广泛应用的单元插值有六面体Lagrange、四面体体积插值法和等参元逆变换插值法[5,9]等。全局插值主要有无限平板样条插值(IPS)[10]、有限表面插值(FPS)[11]、薄板样条插值(TPS)[12]和径向基函数插值(RBF)[13],全局插值可避免网格单元或节点间的搜索过程。
局部插值要预先对网格进行搜索以确定与待插值节点匹配的网格单元或节点。传统网格搜索采用直接搜索方式,即不采用或采用简单的数据结构索引并搜索网格,如Naranjo等[14]采用的简单分层映射方式。高精细流固耦合模拟中流体域网格和固体域网格数量巨大,且每次迭代都涉及大规模的网格搜索计算,所以网格搜索占据整个耦合计算过程的大部分时间。采用的网格搜索技术会直接影响流固耦合计算效率,所以直接的搜索方式会大幅降低耦合计算效率。另一种是采用合适的数据结构组织大规模网格,广泛应用的3D空间索引有网格索引[15]、八叉树[16]、3D-R树[17]和一些简单混合树[18],其中3D-R树具有自动平衡、适用于外存存储、空间利用率高和查询效率高等优点。
中国数值堆项目CVR1.0的热工水力软件PACA对流体域进行求解计算后会输出孤立的网格节点,通过这些节点不能直接还原出流体域网格的拓扑结构。因此,采用基于节点插值中的DWA方法[6-8]为结构力学软件HARSA的固体域网格节点(待插值节点)进行插值计算,得到其承受的压力。本研究采用改进3D-R树索引大规模流体域网格节点,并利用高效搜索算法提高固体域网格节点的插值计算效率。进一步利用HARSA对插值结果进行固体流致振动计算并用Archard模型对固体振动进行磨损评估。
1 软件介绍
反应堆流固耦合指热工水力和结构力学间的耦合,热工水力部分使用中国数值堆项目CVR1.0研发的计算流体力学软件PACA,结构力学部分使用CVR1.0研发的结构力学软件HARSA。PACA和HARSA的耦合中,前者计算关注的是燃料棒周围流体域的变化,而后者计算关注的是作用在燃料棒上的压力及压力对燃料棒造成的影响。
1.1 热工水力模拟软件PACA
单相精细化计算流体力学热工水力模拟软件PACA采用精确大涡模拟模型的高精度谱元方法,可对反应堆堆芯进行精确的数学物理建模,能精确求解反应堆容器内部的压力场、流场和温度场。PACA的计算过程、网格模型和输出数据结构示于图1。由图1a可见,PACA的求解计算过程包括预处理、计算求解、后处理3部分。
预处理部分的“网格分区”将流体域离散化为四面体网格,且每个四面体网格又被细化为4个六面体网格,部分流体域的六面体网格示于图1b。预处理结束后,每个节点都有1个位置坐标(x,y,z)。之后将流体域的六面体网格传递给计算求解部分进行求解计算,计算结束后每个节点都有1个速度U、压力p和温度T。
后处理部分会输出求解计算生成的流体域网格文件,即.fld文件。如图1c所示,.fld文件由head和body两部分构成。在head部分,num为总网格单元数,inf为body中记录的信息类型。body的每一行记录1个节点的信息:(x,y,z)为节点的位置坐标,Ux、Uy、Uz为节点对应的矢量速度U分别在x、y、z轴方向的分量,p和T为节点上的压力和温度。

图1 PACA的计算过程、网格模型和输出数据结构Fig.1 Calculation process, mesh model and output data structure of PACA
1.2 结构力学模拟软件HARSA
反应堆结构力学高保真有限元模拟软件HARSA可对堆芯组件在高温、辐照、流体等因素作用下的力学行为进行模拟。HARSA的计算过程、网格模型和输出数据结构示于图2。由图2a可见,HARSA的计算流程大致分为预处理、计算求解和后处理3部分。
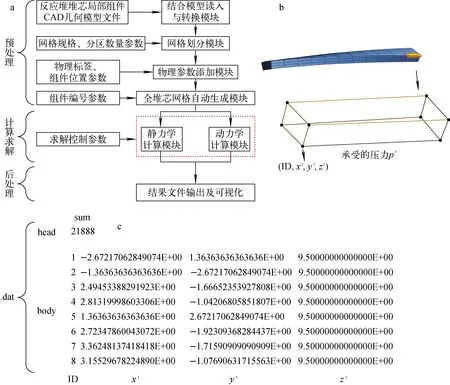
图2 HARSA的计算过程、网格模型和输出数据结构Fig.2 Calculation process, mesh model and output data structure of HARSA
预处理部分的“网格划分模块”将燃料棒离散化为六面体网格,部分燃料棒的六面体网格示于图2b,每个网格节点都具有1个位置坐标(x′,y′,z′)。HARSA使用1个.dat文件存储燃料棒上需要进行插值计算的网格节点,即待插值节点,文件结构如图2c所示。其中,head部分记录待插值节点总数sum,body的每一行记录1个待插值节点的位置信息。插值算法需根据待插值节点附近的流体域网格节点及各节点的压力p,为每个待插值节点计算其承受的压力p′。
1.3 插值过程
HARSA和PACA预处理计算后的燃料棒和流体域网格的密度和大小均不匹配,使得两套网格不能在耦合界面上直接进行信息交换。因此,需借助网格插值技术将流体域网格上的压力信息进行转换并传递到燃料棒的网格上。PACA输出的流体域网格节点数目非常大,传统插值方式非常耗时。因此,研究利用3D-R树索引大规模流体域网格节点,以加快对燃料棒上待插值节点压力的求解计算,从而提高整体流固耦合效率。网格插值过程如图3所示,整个插值过程包括2个阶段,即索引构建阶段和查询处理阶段。
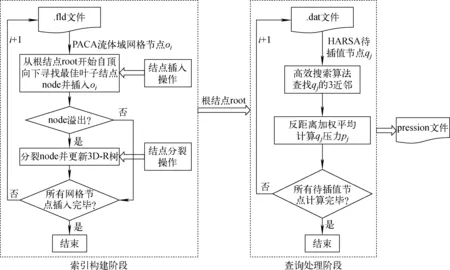
图3 网格插值过程Fig.3 Mesh interpolation process
1) 索引构建阶段
将所有流体域网格节点采用逐一插入的方式构建3D-R树,任意网格节点oi由位置坐标及其对应的速度、压力、温度描述。oi的插入过程为:从根结点root开始自顶向下查找最佳叶子结点并将oi插入其中,之后判断此叶子结点是否溢出,溢出则执行结点分裂操作并更新树,否则继续插入新的网格节点直至构成完整3D-R树。最佳叶子结点指插入oi后周长增加最小的叶子结点。
2) 查询处理阶段
对于每个待插值节点qj,依据高效搜索算法查找距离它最近的3个流体域网格节点,之后利用式(1)计算qj对应的压力pj,直至为所有待插值节点计算出对应的压力。
2 基于改进3D-R树的网格插值
根据PACA输出的流体域网格节点无法直接还原网格拓扑结构,本研究采用基于节点插值中的反距离加权平均法DWA[6-8]为燃料棒上的待插值节点计算对应的压力。DWA首先为待插值节点查找距离它最近的几个流体域网格节点,之后分别以这些流体域网格节点到该待插值节点的距离为权重,计算待插值节点对应的压力。燃料棒-流体域网格模型的可视化示意图如图4所示,左侧为1组燃料棒-流体域离散后的网格模型,右侧为其局部放大。图4中qi为燃料棒上某待插值节点,对流体域网格节点搜索获得距离qi最近的3个节点,分别为os、om、on,根据式(1)计算qi的压力pi。

图4 燃料棒-流体域网格模型的可视化示意图Fig.4 Visualization schematic diagram of mesh model in fuel rod-fluid domain
(1)
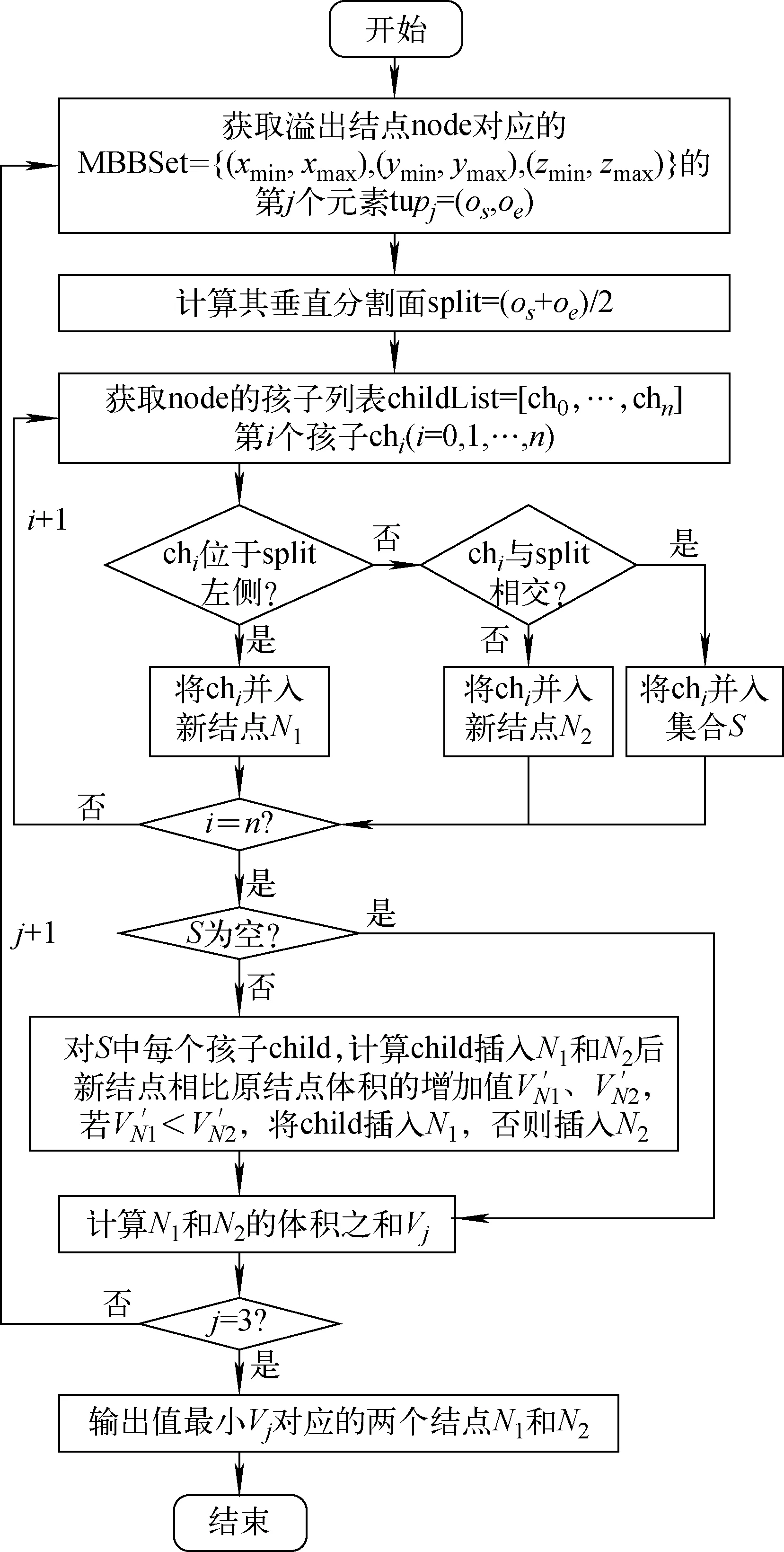
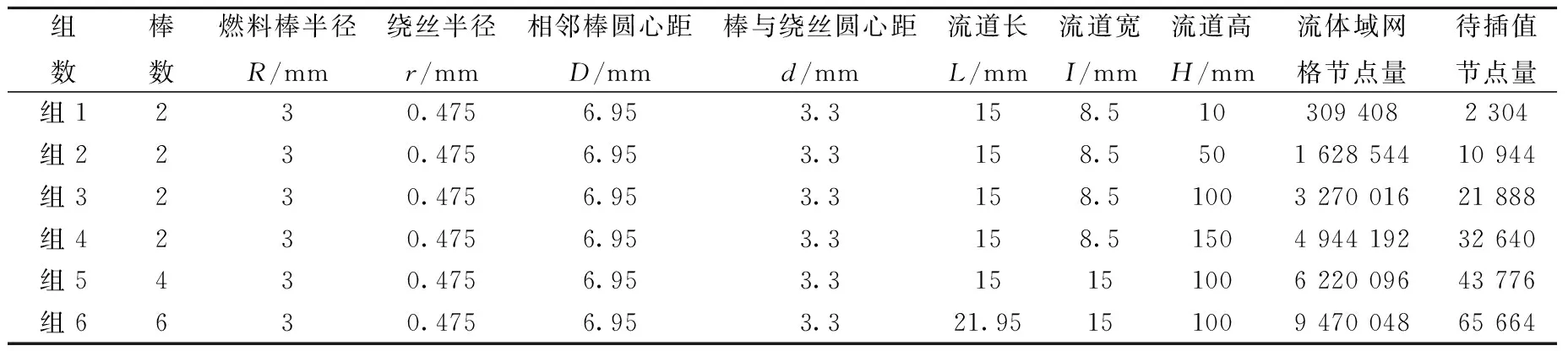
式中:j=s,m,n;ps、pm、pn分别为os、om、on的压力;ds、dm、dn分别为os、om、on与qi的距离,且dm 本研究利用3D-R树索引堆芯空间中的大规模流体域网格节点,1棵3D-R树在2D空间中的投影示意图如图5所示。3D-R树是一棵高度平衡树,除根结点外任意结点的孩子结点数不得大于预设扇出值M,若结点孩子数大于M,则结点溢出,需执行结点分裂操作保证树平衡。树中结点使用最小包围盒(MBB)描述,MBB由1个6元组(xmin,xmax,ymin,ymax,zmin,zmax)表示,MBB为恰好包围空间点的最小盒。3D-R树将位置靠近的空间点聚集构成叶子结点,它们对应于空间中最小的包围盒,如图5a中的实线矩形;继续将空间中较小的包围盒聚集构成上层较大的包围盒,即中间结点,如图5a中虚线矩形;如此逐层聚集最终得到1个包含所有空间点的最大包围盒,即根结点。 a——3D-R树的2D平面投影;b——对应树型结构图5 3D-R树在2D空间投影结构示意图Fig.5 Schematic diagram of 3D-R tree projection in 2D space 3D-R树允许结点间存在重叠,这会使访问空间点分布不均匀的区域时出现大量重复路径,影响查询效率。传统3D-R树通过大量复杂比较计算,将分裂得到的两个新结点包围盒周长之和最小作为评判依据进行结点分裂,以此寻求较小的重叠区域。但PACA的流体域网格节点数目巨大、密度大且分布相对均匀,建树时会执行大量的结点分裂操作,所以传统分裂策略会严重影响建树效率。为此,基于流体域网格节点密度大且分布相对均匀的特点,设计了一种体积均分结点分裂方式,其通过简单计算即可得到包围盒体积之和较小的两个新结点,有效降低了索引构建时间。 体积均分结点分裂过程如图6所示,node为1个溢出结点,其包围盒(xmin,xmax,ymin,ymax,zmin,zmax)由平行于坐标轴的3类边构成,它们的范围分别为xmin→xmax、ymin→ymax、zmin→zmax,构成集合MBBSet={(xmin,xmax),(ymin,ymax),(zmin,zmax)}。对于MBBSet中的第j个元素tupj=(os,oe),首先计算其垂直分割面split,之后遍历node的每个孩子chi,若chi位于split左侧,将chi并入新结点N1;若位于split右侧,将chi并入N2;若与split相交,将其暂存入集合S。处理完node的所有孩子后,判断S是否为空,为空则计算N1和N2体积和Vj,否则将S中的每个孩子插入N1或N2并计算N1和N2体积和Vj。处理完MBBSet中所有元素后输出Vj最小的N1和N2,它们是分裂得到的两个新结点。 图6 新树结点分裂策略流程图Fig.6 Flow chart of new splitting strategy for tree node 传统插值采用直接搜索方式为每个待插值节点查找距离它最近的3个流体域网格节点,时间复杂度为O(3mn),其中n为流体域网格节点数,m为待插值节点数。由于流体域网格节点数巨大,直接搜索方式非常耗时。为此,使用基于(改进)3D-R树的快速搜索方式。 基于(改进)3D-R树的网格搜索流程示于图7,使用优先队列PrioQue来加速搜索。PrioQue中存储树结点及其到待插值节点qi的最短距离,距离越小优先级越高。初始时,PrioQue中存储根结点root及其到qi的距离。首先从PrioQue中弹出优先级最高的元素node,若node为结点类型,则遍历node的所有孩子,对每个孩子chi,计算chi到qi的距离dist(chi,qi)并入队。若node为非结点类型,则它是一个最近邻,将node存入集合R。判断近邻数R(集合R中的元素个数)是否为3,为3则计算待插值节点qi的压力pi,否则继续从PrioQue中弹出优先级最高的元素并重复上述过程。 图7 基于(改进)3D-R树的网格搜索流程图Fig.7 Mesh search flow chart based on (improved) 3D-R tree 利用表1所列6组数据进行实验,测试了燃料棒上待插值节点的插值计算效率。进一步利用HARSA计算燃料棒在流体压力作用下的流致振动变化,并利用Archard模型评估棒束流致振动变化下的磨损程度。PACA预处理计算后的流体域网格模型及参数示于图8。 图8 流体域网格模型展示Fig.8 Visualization of fluid domain mesh model 表1 实验用到的数据Table 1 Data used in experiment 本研究测试了基于直接搜索、3D-R树和改进3D-R树3种插值方式(分别用BaseLine、RTree和ImRTree表示)在不同条件下的性能。 燃料棒长变化时,构建3D-R树和改进3D-R树执行的总结点分裂次数示于图9a。棒长增大时,RTree和ImRTree执行的结点分裂次数均增大;棒长相同时,两者执行的总结点分裂次数相近。燃料棒长变化时,RTree和ImRTree执行结点分裂消耗的总时间示于图9b。可见,为PACA输出的流体域网格节点构建索引时,改进结点分裂效率远高于传统结点分裂效率。 图9 燃料棒长变化时结点分裂次数和结点分裂时间Fig.9 node splitting times and time vs fuel rod length 燃料棒数变化时,3种网格插值消耗的时间示于图10a。可见,BaseLine消耗时间最多,ImRTree消耗时间最少,RTree消耗时间位于两者之间。由于流体域网格节点数量和密度均较大,建树时要进行大量复杂的结点分裂计算,因此RTree消耗的时间较多。ImRTree采用简单的体积均分结点分裂方式,所以消耗的时间最少。燃料棒长变化时,3种网格插值消耗的时间示于图10b。棒长增大时,BaseLine的时间消耗最大,ImRTree的时间消耗仍最少,而RTree的时间消耗仍位于前两者之间。由图10可见,ImRTree和RTree在高精细插值计算中更具优势。 图10 燃料棒数或长度变化时的插值时间Fig.10 Interpolation time vs fuel rod number or length 当树中结点孩子数大于预设扇出值M时,会执行结点分裂操作及树的更新操作。当M设置不合适时,可能会执行频繁的分裂及更新操作影响建树效率,从而影响插值计算效率。本文选取表1中组4和组6两组数据并选取M为25、50、75,测试基于RTree和ImRTree的插值效率。M变化时插值消耗的时间如图11所示。由于ImRTree的结点分裂消耗时间较少,M变化时ImRTree的插值效率仍明显高于RTree的插值效率。当M=25时,由于RTree和ImRTree执行的分裂及更新操作均最少,所以两者插值效率均最高。当M≥50时基于ImRTree的插值效率趋于平稳,而M增大时基于RTree的插值效率降低明显(图11b)。 图11 M变化时插值消耗的时间Fig.11 Time consumed by interpolation vs M 燃料棒受到周围流体域施加的交替相间的压力后会产生往复运动,燃料棒的这种振动会伴随着棒束间的磨损。本文选取表1中组3的模型,利用上述网格插值方式将0~3 s流体域网格节点的压力转换为燃料棒上待插值节点对应的压力,并将插值结果传递给HARSA进行结构力学计算,得到0~3 s燃料棒上待插值节点的位移、速度、加速度变化。进一步利用Archard模型对棒束振动造成的磨损程度进行评估。Archard模型是工程中广泛应用的磨损模型之一,其形式为: V=SFL/3H (2) 式中:V为磨损体积;S为磨损系数;F为与接触面垂直的接触力;L为总的滑动距离;H为材料硬度;3为适用于半球形磨粒的形状因子。 燃料棒束在0~3 s的位移变化示于图12。0~1 s,棒束位移变化明显,最大位移出现在左侧燃料棒顶端,为27.83 mm,最小位移发生在棒束底端,为6.854×10-22mm。如图12b、c、d所示,1~3 s棒束的最大位移未发生变化,1~2 s棒束的最小位移降至6.411×10-22mm,2~3 s棒束的最小位移增至7.967×10-22mm。由于1~3 s各时刻棒束对应位置压力相差过小,图12b、c、d棒束上位移分布相似。 图12 燃料棒束在不同时刻的位移响应Fig.12 Displacement response of fuel bundle at different time 燃料棒束在0~3 s的速度和加速度变化分别示于图13、14。由图13a、b和图14a、b可看出,初始0~1 s,棒束在周围流体域的压力作用下速度(加速度)变化明显,最大速度(加速度)出现在棒束顶端,为56.2 mm/s(113.5 mm/s2);最小速度(加速度)出现在棒束底端,为1.384×10-21mm/s(2.794×10-21mm/s2)。可见,0~1 s时棒束顶端承受的压力最大,底端承受的压力最小,且在流体域的压力作用下棒束开始发生振动。 由图13b、c、d可知,1~2 s最小速度增至3.405×10-21mm/s,2~3 s最小速度降至2.387×10-21mm/s。1~3 s棒束最小速度呈先增后降的趋势,这是由于棒束不同位置受到的流体域压力不同导致的。由图14b、c、d可知,1~2 s最大加速度增至338.3 mm/s2,最小加速度增至1.086×10-20mm/s2;2~3 s最大加速度增至563.1 mm/s2,最小加速度增至3.131×10-20mm/s2。1~3 s棒束的最大和最小加速度均呈增大趋势,可见棒束顶端和底端的受力是一直增大的。 图13 燃料棒束在不同时刻的速度响应Fig.13 Velocity response of fuel bundle at different time 图14 燃料棒束在不同时刻的加速度响应Fig.14 Acceleration response of fuel bundle at different time 可见,在周围流体域压力作用下燃料棒束的不同位置受力程度不同,这导致棒束不同位置上的速度和加速度响应不同,从而导致棒束不同位置上的位移响应不同。燃料棒束在这种不同程度的交替压力作用下会产生往复运动,即发生流致振动。 根据燃料棒束0~3 s的振动变化,进一步对表1中组3的两根燃料棒进行磨损评估。提取燃料棒绕丝与相邻燃料棒包壳管间的接触力为980.523 N,滑移距离分别为11.009 51 mm和11.009 37 mm,材料硬度取20,磨损系数取2×10-9mm3/J。根据式(2)所示磨损评估公式,计算得到组3棒束中左侧燃料棒的磨损体积为3.598 36×10-7mm3,磨损深度为2.451 31×10-8mm;组3棒束中右侧燃料棒的磨损体积为3.598 31×10-7mm3,磨损深度为2.451 31×10-8mm。 本研究使用3D-R树索引PACA计算输出的大规模流体域网格节点,实现了对燃料棒上待插值节点的高效插值计算。通过分析PACA流体域网格特点和3D-R树中的结点分裂方式,设计了一种简单的体积均分结点分裂策略。实验表明,基于此改进3D-R树的插值效率明显高于基于3D-R树和传统插值的效率。利用HARSA根据插值结果进行了燃料棒的流致振动计算,并用Archard模型计算了燃料棒的磨损程度。本研究对堆芯安全设计、延寿等具有重要意义。后续工作将深入研究燃料棒的振动对流体域产生的影响以设计高效的流体域网格更新策略。2.1 改进的3D-R树

2.2 网格搜索

3 实验验证及分析

3.1 网格插值效率验证
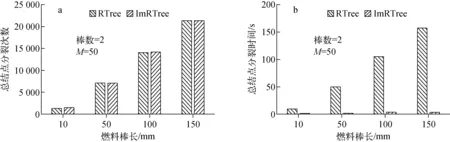


3.2 流致振动磨损评估
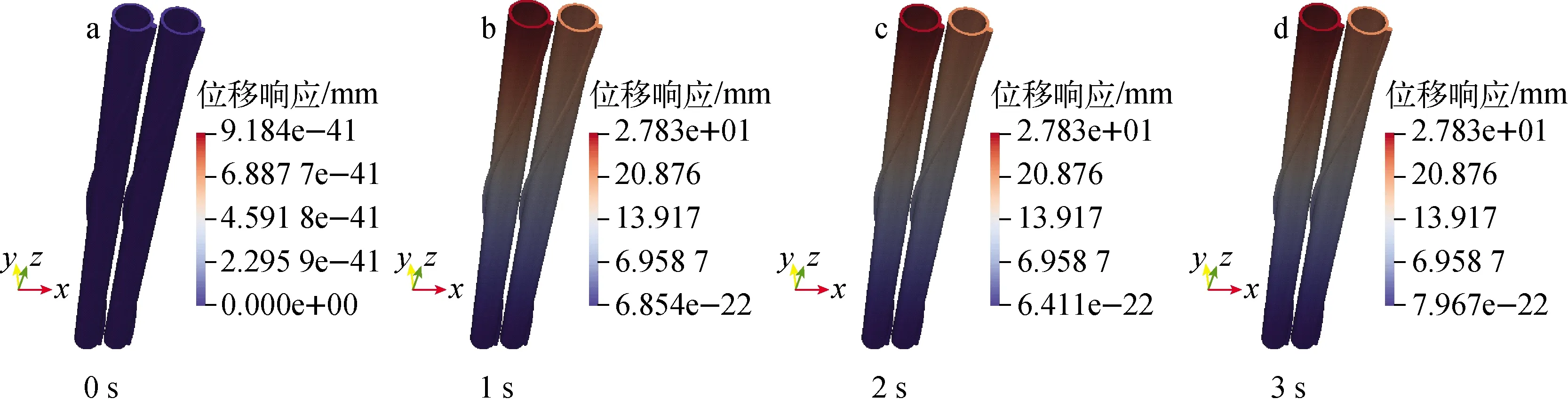
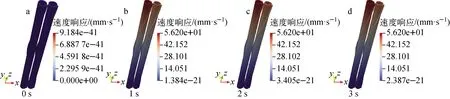
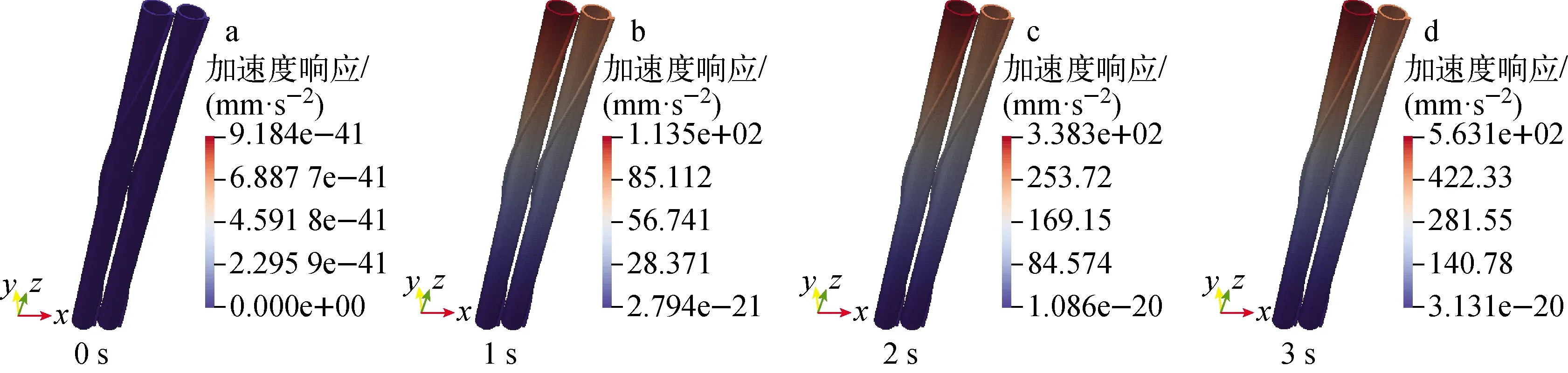
4 总结
