秸秆-薯渣混合物料应力松弛分数阶模型的建立及参数分析

郭文斌，王志鹏，候智博，胡 凡，王春光，齐文静

秸秆-薯渣混合物料应力松弛分数阶模型的建立及参数分析

郭文斌，王志鹏，候智博，胡 凡，王春光※，齐文静

（内蒙古农业大学机电工程学院，呼和浩特 010018）

为更加精确地解析农业松散物料压缩时表现出的应力松弛行为及松弛后的成型效果，简化应力松弛模型并获得更加直观的应力松弛特征参数，该研究将Riemann-Liouville分数阶微积分理论引入农业松散物料流变学特性研究中，以农业生产后残留的玉米秸秆与马铃薯废渣为研究对象，推导建立了用于描述秸秆-薯渣混合物料应力松弛特征的分数阶模型，并以松弛比与松弛时间比率为试验指标，完成了混合物料在不同压缩密度下的应力松弛试验，利用所建立分数阶模型对应力松弛试验曲线进行了拟合回归分析，并与广义Maxwell模型的拟合结果进行了对比与参数相关分析。结果表明：1）分数阶模型可准确描述秸秆与薯渣混合物料的应力松弛过程，其对松弛曲线的拟合精度高于五元件广义Maxwell模型，决定系数2介于0.996 4～0.999 5之间。2）分数阶模型仅有两个模型参数，分数阶阶数与粘弹性系数，其中与应力松弛后残留弹性的占比、松弛比均极显著负相关，可直接用于表征物料松弛后的永久变形程度，预测其成型效果；与弹性模量及粘性系数、松弛时间比率均极显著正相关，可用于表征混合物料的粘弹性特征及其应力松弛快慢程度。该研究成果推动了分数阶微积分理论在农业松散物料流变学特性研究领域的应用，通过分数阶模型建立了秸秆-薯渣混合物料的应力松弛特性与成型效果的联系，可为进一步改进农业松散物料成型方法、获取最佳成型条件提供依据。

应力松弛；模型；粘弹性；秸秆；薯渣；分数阶计算

0 引 言

玉米秸秆与马铃薯废渣是农产品收获与生产加工后剩余的典型农业废弃物料，由于具有容积密度小、群体松散、可压缩性好等特点[1-3]，再利用时常需要进行压缩处理，制成饲料、燃料、复合材料等各类生物质产品。对此类群体呈松散态的农业物料进行压缩时，为减少能耗、提升成型效果，常借助流变学试验方法研究物料的应力松弛与蠕变特性[4-6]，进而优化其压缩工艺及设备[7-9]。在分析农业松散物料的应力松弛特性时，已有研究多以弹性元件（spring）与粘性元件（dashpot）串联而成的Maxwell模型为基础建立应力松弛模型[10]，例如广义Maxwell模型[11-13]、Zener模型[14-15]、Poynting Thomson模型[16-17]。上述模型的组成元件越多，应力-时间试验曲线的拟合精度也越高[18]，因此针对农业物料建立的此类应力松弛模型的元件数量常在3个以上，回归拟合后所得的模型参数也相应较多。为简化模型参数，更加准确、直观地描述农业松散物料压缩过程中的应力松弛行为，基于分数阶微积分理论建立的流变学模型开始被应用于描述和分析农业物料受压时表现出的粘弹特性[14,19]。

分数阶微积分理论将整数阶微积分推广到了任意阶次，经过多年发展与完善，根据该理论计算得出的分数阶模型逐渐被应用于各相关领域研究。随着研究的深入，分数阶模型全局相关性好、物理意义明确的优点逐渐显现，其可以用较少的模型参数准确反映试验结果，比较适合于描述材料的非线性力学行为，因此Blair和Caffyn早在1949年就将分数阶计算应用在了材料流变学行为的分析上[20]，而Koeller等在几十年后又进一步将其引入了粘弹性特征分析的研究领域，结合传统流变学理论建立了分数阶模型[21-23]。近年来，基于分数阶微积分理论构建流变学模型并进行参数分析的研究，主要集中于岩土材料[24-25]、聚合物[26]、食品凝胶[27]等材料的流变学特性研究领域，而对于群体具有粘弹性特征的松散农业废弃物料，利用分数阶微积分理论构建其应力松弛模型、分析应力松弛特性的研究甚少。

为推进分数阶微积分理论在松散农业废弃物料应力松弛特性研究领域的应用，通过构建应力松弛分数阶模型，更加直观、精确地解析物料的应力松弛行为及松弛后的成型效果，本研究结合秸秆碎料与马铃薯废渣的物性特点，以秸秆-薯渣混合物料为研究对象，进行应力松弛特性分析及分数阶模型研究，拟获取用于表征混合物料压缩成型品质的关键模型参数。

1 材料与方法

1.1 试验材料

试验用玉米秸秆选取内蒙古呼和浩特地区秋冬季收获后自然干燥的整株秸秆，经粉碎机粉碎后含水率为（4±0.1）%，利用冲孔分样筛将碎料筛分至小于3 mm粒度并进行称重。试验用马铃薯废渣取自内蒙古呼和浩特市淀粉加工企业，经前处理后含水率为（65±1）%，为防止物料腐败变质、减少水分散失，试验前将薯渣分装后在2～4 ℃环境下冷藏保存，一周内完成相关试验。

1.2 试验设备与方法

试验设备为DDL200型微机控制电液伺服万能试验机配以自制的可卸料式压缩装置（图1），其中压缩筒底部开有导流孔以便排出气体与水分。参考相关力学试验研究[28]，试验时将分样筛筛分后的秸秆碎料与薯渣以质量配比1∶3进行混合，并通过搅拌机搅拌均匀后，喂入压缩装置，由EDC数字控制器根据计算机程序控制活塞式压头完成轴向加载与保压，加载速率为10 mm/min，保压时间设定900 s，试验结束后抽动抽板，混合物料块通过出料孔完成落料。

为分析分数阶模型参数与物料应力松弛特性及成型效果的联系，选择压缩密度作为试验影响因素，将秸秆与薯渣混合物料加载至不同压缩密度进行松弛，同一密度下重复试验3次，在室温下完成。确定压缩密度水平时参考秸秆与薯渣混合物料的应力-应变试验曲线，计算得出割线模量E与切线模量E[10]，按照E与E比值（模量比）的大小，将应力-应变曲线划分为松散阶段、过渡阶段、压紧阶段[3, 29-30]。为保证成型效果、降低能耗，最终确定应力松弛试验压缩密度水平为进入压紧阶段后的700、800、900、1 000、1 100 kg/mm3。

1.3 试验指标

为分析应力松弛特性参数与物料块成型效果的联系，将松弛比作为试验指标之一，其值为应力松弛试验保压时物料压缩密度与出模5 h后物料块松弛密度[31]的比值，计算如公式（1），松弛比越小压缩密度与松弛密度越接近，物料的成型效果越好。

式中S为松弛比；为压缩密度，kg/m3；为松弛密度，kg/m3。

为衡量混合物料应力松弛快慢，分析其与应力松弛分数阶模型参数的联系，以应力松弛时间比率作为另一试验指标，其为松弛过程中初始应力与应力松弛时间的比值，即初始应力在单位松弛时间内衰减的量[16]，计算如公式（2），松弛时间比率越大，物料应力松弛越快。

式中S为应力松弛时间比率，MPa/s；为初始应力，MPa；为应力松弛时间，s。

1.4 分数阶应力松弛模型的建立

由于秸秆、薯渣等农业松散物料压缩过程中兼有弹性变形与粘性流动的特征，且无明显的屈服点，其永久变形主要来源于物料的粘性流动[16]。因此，依据胡克定律与牛顿定律可得：

近几年，水稻连年增产、种植面积不断扩大，水稻产业得到了大力的发展，也取得了显著的成效。但是栽培的品种单一，病虫害发生加重等问题，难以确保水稻的稳定发展，为此，我们对省内近期育成的水稻品种进行对比试验研究，进一步客观、科学的鉴定品种的特性特征及综合表现，筛选出其中的优良品种，提高粮食综合生产力，推动农场经济的快速发展。

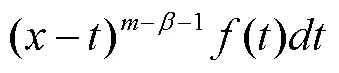
归纳式（3）～（6）得到应力与应变的分数阶模型为

根据式（5）所表达的阶导数的定义，联合式（5）与式（7）推导得出：

式中为虚拟变量（Dummy variable），考虑到应力松弛过程中物料的应变为恒定值[10,16]，故可将应变()替换为常值应变0，进而推导出描述随变化的分数阶模型为

式中()为任意时刻弹性模量，MPa。

1.5 广义Maxwell模型的建立

为分析和验证分数阶模型描述秸秆-薯渣混合物料应力松弛行为的准确性，获取其模型参数与物料松弛过程中粘弹性变化之间的联系。除分数阶模型外，建立被广泛用于描述农业物料应力松弛特性的典型五元件广义Maxwell模型[10,16]如式（11），进行拟合回归分析后，将获取的弹性模量、粘性系数等参数与分数阶模型所得参数进行对比，以解析分数阶模型参数、的含义。

式中1为第一衰变弹性模量，MPa；2为第二衰变弹性模量，MPa；E为平衡弹性模量，MPa；1、2分别为衰变弹性模量对应的粘性系数，MPa·s。由上述模型参数可得应力松弛的初始弹性模量[10]为0=1+2+E。

2 结果与分析

2.1 应力松弛试验曲线

2.2 应力松弛模型参数分析

2.2.1 模型参数对比分析

从模型分析结果可以看出，不同试验条件下分数阶模型和广义Maxwell模型对秸秆-薯渣混合物料应力松弛试验曲线的拟合精度均较高，决定系数2>0.99，其中分数阶模型拟合所得决定系数2（0.996 4～0.999 5），整体高于五元件广义Maxwell模型拟合所得决定系数2（0.995 1～0.995 9），故分数阶模型参数对混合物料应力松弛特性的描述也更为精确。相关研究表明，广义Maxwell模型可以通过增加Maxwell 单元数量进一步提高拟合精度[18]，但单元数量的增加不仅会增加模型参数，

而且会使模型变得更加复杂，对物料应力松弛特性及成型效果的描述更加不直观。因此，与广义Maxwell模型相比，本文推导得出的应力松弛分数阶模型参数较少，仅有、，在对应力松弛特性进行描述时也较为简便，充分体现出了将分数阶微积分理论应用于农业松散物料应力松弛特性分析的优点。

表1 应力松弛模型非线性回归分析结果

2.2.2 参数间相关性分析

相关性分析是研究参数间关系密切程度的统计分析方法，可计算出用于表示参数间相关程度的相关系数，并通过对其进行显著性检验、求得显著性概率来做出统计学推断。本研究分别将不同压缩密度条件下应力松弛试验所得分数阶模型参数与广义Maxwell模型参数联系起来进行相关性分析，结果如表2所示，、与弹性模量及粘性系数均有显著的相关关系，其中1、2、0、1、2与呈极显著正相关，再次体现出与物料粘弹性特征之间的联系，表明其可用于描述秸秆-薯渣混合物料应力松弛过程中表现出的粘弹性。此外，由于平衡弹性模量E表征了应力松弛过程中应力衰减至趋于平衡时物料的残留弹性[10]，故平衡弹性模量与初始弹性模量的比值E/0反映了应力松弛后物料残留弹性占应力松弛前物料初始弹性的比例；因此根据相关性分析结果（表2），分数阶阶数与E/0呈极显著负相关，说明了越小，应力松弛趋于平衡时混合物料残留的弹性占比越大，松弛过程中衰减掉的弹性占比越小，产生永久变形的程度也越小。上述分析结果揭示了分数阶模型参数、所蕴含的物理意义，为利用松弛特性参数预测混合物料成型效果、优化成型工艺提供了思路。

表2 分数阶模型和广义Maxwell模型参数相关性分析

注：**和*分别表示极显著相关（<0.01）与显著相关（<0.05）。

Note: ** and * indicate that the correlation are extremely significant (<0.01) and significant (<0.05), respectively.

2.3 分数阶模型参数与松弛试验指标的联系

为进一步解析分数阶模型参数、与混合物料成型效果、应力松弛快慢等试验指标的联系，验证参数、所表达的物理意义，图5列出了700～1 100 kg/m3压缩密度条件下的松弛比S与松弛时间比率S，可以看出压缩密度不同时，混合物料应力松弛试验所得S与S虽各不相同，但遵循一定规律。其中压缩密度越大，应力松弛试验保压结束后混合物料块的松弛比S越小，成型效果越好，这是因为压缩密度的增加使得物料压缩过程所需加载力增大、能耗增大[1,12]，对物料的成型起到了积极的作用。而压缩密度越大，混合物料开始松弛时的初始应力0越大，其单位时间内松弛的量也越大，松弛现象越明显，故试验所得松弛比率S越大，混合物料保压后的应力松弛越快。

不同压缩密度条件下应力松弛分数阶模型参数、的大小及变化规律如表1。从总体趋势来看，在其他试验条件相同时压缩密度越大，保压后所得混合物料应力松弛分数阶模型参数、也越大。其中粘弹性系数的变化规律与松弛比率S的变化规律较为相似，且二者极显著正相关（表3），即越大松弛比率S越大，可见粘弹性系数的大小能够反映出以不同压缩密度保压时混合物料应力松弛的快慢。上述结果与弹性模量、粘性系数大小对应力松弛快慢的影响是一致的[32]，因此也再次证明了与弹性模量、粘性系数之间的相关关系。

此外，分数阶模型参数与松弛试验指标的相关性分析结果（表3）显示，、均与松弛比S呈显著负相关，其中分数阶阶数与S为极显著负相关，结合表1、图5也可以看出压缩密度越大，、也越大，松弛比S越小，混合物料变形恢复越小、成型效果越好。因此的大小能够反映出秸秆-薯渣混合物料压至不同压缩密度进行应力松弛后，混合物料的成型效果；该结果进一步印证了与混合物料永久变形程度的联系。

表3 分数阶模型参数与松弛试验指标的相关性分析结果

3 结 论

1）建立了秸秆-薯渣混合物料的应力松弛分数阶模型和广义Maxwell模型。分数阶模型拟合松弛试验曲线所得决定系数2介于0.996 4～0.999 5，高于五元件广义Maxwell模型拟合所得2（0.995 1～0.995 9），因此其拟合效果更好，对混合物料应力松弛过程的描述更为精确。

2）分数阶模型仅有分数阶阶数与粘弹性系数两个参数，与广义Maxwell模型参数的相关性分析表明，与弹性模量、粘性系数呈极显著正相关，可用于描述混合物料松弛过程中的粘弹性特征；与平衡弹性模量占比E/0呈极显著负相关，越小物料应力松弛后残留弹性占比越大，松弛过程衰减掉的弹性占比越小，产生不可恢复变形也越小，因此可用于描述混合物料的永久变形程度。

3）将松弛比S、松弛比率S分别与分数阶模型参数、进行相关性分析，得出与表示混合物料成型效果的S呈极显著负相关（0.01）；与表示应力松弛快慢的S呈极显著正相关（0.01）。印证了模型参数相关分析所得结果，进一步明确了成型效果、松弛快慢与分数阶模型参数的联系。

综上，本文基于分数阶理论建立的应力松弛模型，能更精确、直观地描述秸秆-薯渣混合物料应力松弛时的粘弹性变形过程，所得参数可用于表达和预测物料应力松弛快慢及松弛后成型效果，为加工混合物料时选择合理压缩方式、压缩频率等提供参考，以促进低成本混配成型技术的发展。

[1] 范林，王春光，王洪波，等. 揉碎玉米秸秆可压缩性研究[J].农业机械学报，2008，39(11)：76-80.

Fan Lin, Wang Chunguang, Wang Hongbo, et al. Study on compressibility of crushed corn straw[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(11): 76-80. (in Chinese with English abstract)

[2] 李伟. 揉碎玉米秸秆开式压缩蠕变试验研究[D]. 呼和浩特：内蒙古农业大学，2011.

Li Wei. Study on Creep Properties of Maize Straw Rubbed during Open Compression[D]. Hohhot: Inner Mongolia Agricultural University, 2011. (in Chinese with English abstract)

[3] 高晶晶，郭文斌，郁志宏. 马铃薯渣可压缩性研究[J]. 食品与机械，2018，34(2)：50-53.

Gao Jingjing, Guo Wenbin, Yu Zhihong. Study on the compressibility of potato residue[J]. Food and machinery, 2018, 34(2): 50-53. (in Chinese with English abstract)

[4] 赵桂芝. 苜蓿压缩蠕变特性的试验研究与仿真[D]. 呼和浩特：内蒙古农业大学，2009.

Zhao Guizhi. Study and Simulation on Creep Behavior of Alfalfa[D]. Hohhot: Inner Mongolia Agricultural University, 2009. (in Chinese with English abstract)

[5] 闫翠珍，武国峰，王效华，等. 稻秸高密度压缩过程中应力松弛的试验研究[J]. 农机化研究，2015，37(11)：181-187.

Yan Cuizhen, Wu Guofeng, Wang Xiaohua, et al. The study of rice straw’s stress-relaxation in high density compression[J]. Journal of Agricultural Mechanization Research, 2015, 37(11): 181-187. (in Chinese with English abstract)

[6] 周国栋，杜健民，佘文龙，等. 牧草压缩过程应力松弛试验研究及压缩活塞的力学分析[J]. 农机化研究，2017，39(4)：197-201.

Zhou Guodong, Du Jianmin, She Wenlong, et al. Experimental study on stress relaxation of forage in compression process and mechanics research of compression piston[J]. Journal of Agricultural Mechanization Research, 2017, 39(4): 197-201. (in Chinese with English abstract)

[7] 王春光. 牧草应力松弛时间及其应用[J]. 农业机械学报，2007，38(1)：65-67.

Wang Chunguang. Stress relaxation time of hay and its application[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(1): 65-67. (in Chinese with English abstract)

[8] 王春光，杨明韶，高焕文，等. 牧草在高密度压捆时的应力松弛研究[J]. 农业工程学报，1997，13(3)：48-52.

Wang Chunguang, Yang Mingshao, Gao Huanwen, et al. Study on stress relaxation of hay during baling under high density[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1997, 13(3): 48-52. (in Chinese with English abstract)

[9] 李汝莘，耿爱军，赵何，等. 碎玉米秸秆卷压过程的流变行为试验[J]. 农业工程学报，2012，28(18)：30-35.

Li Ruxin, Geng Aijun, Zhao He, et al. Rheological behavior of chopped corn stalks during rotary compression[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(18): 30-35. (in Chinese with English abstract)

[10] 周祖锷. 农业物料学[M]. 北京：中国农业出版社，1994.

[11] 马彦华，宣传忠，武佩，等. 玉米秸秆振动压缩过程的应力松弛试验[J]. 农业工程学报，2016，32(19)：88-94.

Ma Yanhua, Xuan Chuanzhong, Wu Pei, et al.Experiment on stress relaxation of corn stover during compression with assisted vibration[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(19): 88-94. (in Chinese with English abstract)

[12] Du X X, Wang C G, Guo W B, et al. Stress relaxation characteristics and influencing factors of sweet sorghum: experimental study[J]. Bioresources, 2018, 13(4): 87618774.

[13] Kelly P A. A viscoelastic model for the compaction of fibrous materials[J]. Journal of the Textile Institute Proceedings & Abstracts, 2011, 102(8): 689-699.

[14] Chen L J, Liao N, Xing L, et al. Description of wheat straw relaxation behavior based on a fractional-order constitutive model[J]. Agronomy Journal, 2013, 105(1): 134-142.

[15] Yin Y L, Yang Z H, Shi M L. Complex plane analysis of fractional derivative model and its use for parameter determination of viscoelastic material[C]//Proceedings of 2019 2nd International Conference on Manufacturing Technology, Materials and Chemical Engineering (MTMCE 2019), 2019: 87-94.

[16] 杨明韶. 农业物料流变学[M]. 北京：中国农业出版社，2010：20-36.

[17] 周彦男，陈运平，陈佼佼. 分数阶Poynting-Thomson流变模型研究[J]. 西南科技大学学报，2013，28(1)：31-35.

Zhou Yannan, Chen Yunping, Chen Jiaojiao. Study of fractional Poynting-Thomson rheological model[J]. Journal of Southwest University of Science and Technology, 2013, 28(1): 31-35. (in Chinese with English abstract)

[18] Sajn D, Gersak J, Flajs R. Prediction of stress relaxation of fabrics with increased elasticity[J]. Textile Research Journal, 2006, 76(10): 742-750.

[19] Xu Z, Chen W. A fractional-order model on new experiments of linear viscoelastic creep of Hami Melon[J]. Computers and Mathematics with Applications, 2013, 66(5): 677-681.

[20] Blair G W, Caffyn J E. An application of the theory of quasi-properties to the treatment of anomalous strain-stress relations[J]. The London Edinburgh and Dublin Philosophical Magazine and Journal of Science, 1949, 40(300): 80-94.

[21] Koeller R C. Applications of fractional calculus to the theory of viscoelasticity[J]. Journal of Applied Mechanics, 1984, 51(2): 299-307.

[22] Stiassnie M. On the application of fractional calculus for the formulation of viscoelastic models[J]. Applied Mathematical Modelling, 1979, 3(4): 300-302.

[23] Nonnenmacher T F, Glockle W G. A fractional model for mechanical stress relaxation[J]. Philosophical Magazine Letters, 1991, 64(2): 89-93.

[24] 陈亮，陈寿根，张恒，等. 基于分数阶微积分的非线性黏弹塑性蠕变模型[J]. 四川大学学报：工程科学版，2013，45(3)：7-11.

Chen Liang, Chen Shougen, Zhang Heng, et al. A nonlinear viscoelastic-plastic creep model based on fractional calculus[J]. Journal of Sichuan University: Engineering Science Edition, 2013, 45(3): 7-11. (in Chinese with English abstract)

[25] Kang J, Zhou F, Liu C, et al. A fractional nonlinear creep model for coal considering damage effect and experimental validation[J]. International Journal of Non-Linear Mechanics, 2015, 76: 20-28.

[26] 李明明. 聚合物应力松弛和分数Maxwell模型研究[D]. 兰州：西北师范大学，2008.

Li Mingming. Study on Stress Relaxation of Polymer and Fractional Maxwell Model [D]. Lanzhou:Northwest Normal University, 2008. (in Chinese with English abstract)

[27] Simpson R，Jaques A，Nuñez H, et al. Fractional calculus as a mathematical tool to improve the modeling of mass transfer phenomena in food processing[J]. Food Engineering Reviews, 2013, 5(1): 45-55.

[28] 齐文静. 秸秆与薯渣混合物料应力松弛特性试验研究[D]. 呼和浩特：内蒙古农业大学，2020.

Qi Wenjing. Experimental Study on Stress Relaxation Characteristics of Mixture of Cornstalk and Potato Pulp[D]. Hohhot: Inner Mongolia Agricultural University, 2020. (in Chinese with English abstract)

[29] 吕江南，龙超海，何宏彬，等. 红麻料片的压缩特性及压力与压缩密度的数学模型[J]. 农业机械学报，1998(2)：84-87.

Lv Jiangnan, Long Chaohai, He Hongbin, et al. Compression characteristics of the Kenaf chips and mathematical models of pressure-compression density[J]. Transactions of the Chinese Society for Agricultural Machinery, 1998(2): 84-87. (in Chinese with English abstract)

[30] 李震，闫莉，高雨航，等. 生物质压缩成型过程模型研究现状[J]. 科学技术与工程，2019，19(12)：1-7.

Li Zhen, Yan Li, Gao Yuhang, et al. Research status on biomass compression molding process model[J]. Science Technology and Engineering, 2019, 19(12): 1-7. (in Chinese with English abstract)

[31] 邢献军，李涛，马培勇，等. 生物质固体成型燃料热压成型实验研究[J]. 太阳能学报，2016，37(10)：2660-2667.

Xing Xianjun, Li Tao, Ma Peiyong, et al. Experimental study of hot moldling of densified biofuel[J]. Acta Energiae Solaris Sinica, 2016, 37(10): 2660-2667. (in Chinese with English abstract)

[32] 杜晓雪. 青贮甜高粱秸秆压缩及应力松弛特性试验研究[D]. 呼和浩特：内蒙古农业大学，2019.

Du Xiaoxue. Experimental Study on Compressive and Stress Relaxation Characteristics of Solid Sweet Sorghum Straw[D]. Hohhot: Inner Mongolia Agricultural University, 2019. (in Chinese with English abstract)

中国农业工程学会会员：郭文斌（E041201179S）

Parameter analysis and development of fractional calculus model for stress relaxation of cornstalk and potato residues

Guo Wenbin, Wang Zhipeng, Hou Zhibo, Hu Fan, Wang Chunguang※, Qi Wenjing

(,,010018,)

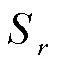
stress relaxation; models; viscoelasticity; cornstalk; potato residue; fractional calculus

10.11975/j.issn.1002-6819.2021.13.032

S216.2

A

1002-6819(2021)-13-0284-07

郭文斌，王志鹏，候智博，等. 秸秆-薯渣混合物料应力松弛分数阶模型的建立及参数分析[J]. 农业工程学报，2021，37(13)：284-290.

10.11975/j.issn.1002-6819.2021.13.032 http://www.tcsae.org

Guo Wenbin, Wang Zhipeng, Hou Zhibo, et al. Parameter analysis and development of fractional calculus model for stress relaxation of cornstalk and potato residues[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(13): 284-290. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.13.032 http://www.tcsae.org

2021-01-17

2021-06-30

国家自然科学基金资助项目（31960365；51766016）；国家重点研发计划项目（2016YFD0701704）；内蒙古自治区高等学校研究项目（NJZY20045）

郭文斌，博士，副教授，硕士生导师，研究方向为农业物料力学特性。Email：wenbingwb2000@sina.com

王春光，博士，教授，博士生导师，研究方向为农牧业机械智能化。Email：nndjdwcg@126.com