受降雨影响的浅水泥沙颗粒起动规律

肖 克，杨奉广，聂锐华，黄 尔，王协康，刘兴年，彭清娥

受降雨影响的浅水泥沙颗粒起动规律

肖 克，杨奉广※，聂锐华，黄 尔，王协康，刘兴年，彭清娥

（四川大学水力学与山区河流开发保护国家重点实验室，成都 610065）

山区浅层水流深度极浅且移动缓慢，降雨条件下其泥沙输移现象尚不明确。为探明受到降雨影响下的浅水河流均匀沙起动问题，该研究假设雨滴落入河道后会影响到整个水流区，形成雨滴群与水流混合的流体，从孔隙介质流理论入手，假设当降雨存在时床面泥沙颗粒增加了向上的附加力，进一步分析泥沙颗粒的受力情况，推导出层流水流泥沙颗粒起动关系表达式。从含沙水流流速分布规律得到启发，雨滴落入层流水流的状态类似于含沙水流，当降雨存在时层流水流流速分布仍然满足线性关系。利用无降雨泥沙起动经典试验数据，确定了拖曳力系数以及上举力系数，发现两者都是沙粒雷诺数的函数。利用已有研究的降雨实测数据，求出了8种降雨强度（0.254～152.4 mm/h）下的雨滴直径分布概率密度表达式（2=0.998），进而求出雨滴的平均直径表达式，并给出受降雨影响的层流水流泥沙颗粒起动切应力计算模型。该研究模型表明降雨的存在使得泥沙起动所需的临界摩阻流速减小。通过与已有研究进行对比分析，该研究建立的受降雨影响的浅水泥沙颗粒起动计算公式具有最高的精度，平均误差仅为14.8%，能够为山区水沙灾害防治提供理论支撑。

降雨；切应力；泥沙颗粒；摩阻流速；相对暴露度

0 引 言

中国西南山区处于地震多发区，通常震后地表富集大规模松散堆积体，受降雨影响，堆积坡面会形成浅层水流，产生大量泥沙进入河道，容易造成大量的泥沙输移[1]。当泥沙被带入浅水河道后，由于水深一般很小，降雨会引起水流运动特性的变化，进而影响河道中泥沙颗粒的运动[2]。这些进入河道的泥沙经水流输移，会淤积附近的建筑物和道路、桥梁等，严重时甚至会阻塞河道，造成洪水溢流。因此研究降雨条件下山区浅层水流的泥沙起动问题，能够为山区河流泥沙灾害防治以及河道修复提供理论支持。

当水流加强到一定程度以后，河道中的泥沙就开始移动，此时的水流和泥沙条件即泥沙起动条件[3-5]。泥沙起动的水力学变量表现主要有起动切应力和起动流速两种。泥沙起动规律往往从泥沙颗粒临界状态的受力分析入手，结合试验推导出起动时所需的无因次切应力，其中较具代表性的是希尔兹曲线[5-6]。希尔兹曲线的优点是物理机制明确，推导简单，国内众多学者都对其进行了理论推导和试验研究。褚君达[7]对国内外25种典型的泥沙起动条件进行理论分析，将其转化为无因次起动切应力的形式，得出无黏性均匀沙无因次起动切应力变化范围为0.023～0.072。杨奉广等[6]推导建立了希尔兹曲线统一表达式，计算公式与试验数据吻合度高，并将其应用于实际的河道冲刷防治中，但是由于其使用的变量是水流摩阻流速，不利于直接应用于工程。为了方便工程应用，以泥沙颗粒受力平衡为基础，结合水流流速分布规律，科研工作者导出了以断面流速表示的起动流速表达式[3,8]。就天然均匀沙而言，在起动流速研究方面，聂锐华等[9]将国内外现有的不同泥沙起动条件进行转换，得出统一的均匀沙起动流速公式，其研究表明泥沙颗粒起动流速与泥沙粒径的1/3次方成正比，与水深的1/6次方成正比。

以上研究都是集中在无降雨条件下，而降雨条件下浅层水流泥沙起动规律的研究较少。Li等[10]探索了降雨对于层流水流条件下泥沙颗粒起动情况的影响，结果表明，在雨滴的影响下，河道底部的泥沙更容易起动。韩浩等[11]从“雨滴落到地面上会增加一个雨滴侵蚀力”的概念出发，假设水深较小时，雨滴侵蚀力仍然存在，导出了紊流条件下的均匀沙起动流速表达式。该研究表明，降雨能减小浅水泥沙起动流速，使泥沙更易起动，但紊流条件下河水比较深，此时再考虑雨滴侵蚀力不太妥当。赵春红等[12]将降雨对坡面薄层水流中泥沙起动的影响归结为雨滴撞击力最大值，结合受力分析，推导出降雨条件下非粘性均匀沙泥沙起动流速公式，发现降雨能够降低坡面泥沙起动流速，促进泥沙起动，但对于坡面流流速分布规律仍采用明渠均匀流流速分布公式，没有考虑到降雨的影响。

鉴于山区浅层水流的特点，本研究概化出受降雨影响下的山区浅水河道泥沙颗粒受力图景，结合受力平衡揭示泥沙起动的物理机制，构建泥沙颗粒起动条件表达式，并用已有研究中的试验数据对本文公式进行对比验证，以期为山区河流保护和山区水沙灾害防治提供理论支撑。

1 理论推导

图1a显示了雨滴落入山区浅水河道的情形，河道的平均流速为（m/s），降雨强度为（mm/h）。由于山区浅层水流深度极浅且移动缓慢，常常以层流的方式流动[13]。基于此，本文假设雨滴落入河道后会影响到整个水流区，形成如图1a所示的雨滴群与水流混合的流体。该过程类似于群体泥沙颗粒的沉降，可看成悬浮雨滴群以v的速度向床面沉降。由于河道水流中的雨滴群与河道水流在竖直方向上有了相对速度v，如果把这个雨滴群看做是静止的孔隙介质，则可以概化为如图1b所示的向上入渗的孔隙介质渗流。

由于雨滴的影响，河床泥沙颗粒会受到一个附加力，但是在已有研究中其缺少具体的物理意义[10-12]。为进一步探究降雨对泥沙颗粒的作用机理，本文借助图1的物理图景，结合孔隙介质理论，将受降雨影响的河道中泥沙颗粒受到的附加力表示成渗流力的形式[14-15]，如图2所示。其表达式为

式中I为降雨附加力，N；I为渗流水力坡度[14,16]，可以理解为由于降雨额外产生的水力坡度；1-为图1a所示的河流水体（单位河长）中雨滴颗粒总体积与水体总体积的比值，属于无量纲变量；I为水流中雨滴颗粒的粒径，m；为水的密度，kg/m3；为重力加速度，取9.81 m/s2。

处于水流中的泥沙颗粒除了受到向上的额外附加力外，还受水流的拖曳力D（N）、上举力L（N）以及颗粒本身的重力（N）[3-5,17]，如图2所示。它们的表达式分别为

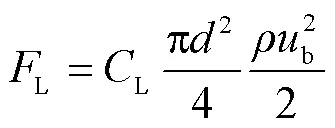
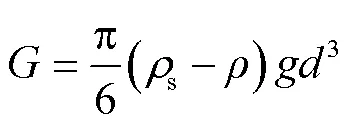
式中为泥沙颗粒粒径，m；D为拖曳力系数；L为上举力系数；b为瞬时近底流速，m/s；s为泥沙颗粒的密度，kg/m3。从图2还可以看出，与紊流水流中泥沙颗粒受力不同，层流中泥沙颗粒所受的上举力是向下的，这一点已经被试验[13]证实。

底部泥沙颗粒所受拖曳力的作用位置尚未有定论，总体而言，其变化范围在距离泥沙颗粒顶端0.3～0.5之间[3]，本文采用杨奉广等[18]的研究结果，取作用点为/3，如图2所示。

注：I为附加渗流力，N；D为拖曳力，N；L为上举力，N；为泥沙颗粒自重，N；L、L为受力力臂，m；为暴露度。

Note:Iis the additional seepage force, N;Dis the drag force, N;Lis the uplift force of flow, N;is the dead-weight of sediment particles, N; LandLare the arm of force, m;is the exposure.

图2 泥沙颗粒受力示意图

Fig.2 Sketch map of forces exerted on the sediment particles

对泥沙颗粒的滚动起到正向效应的是水流拖曳力F和降雨附加力I，而水流上举力L和泥沙颗粒自重阻碍了泥沙颗粒的滚动。当泥沙颗粒处于临界状态时，由滚动的力矩平衡方程可以得到起动概率公式[18]

式中为泥沙颗粒起动概率；L、L为受力力臂，m，分别由图2几何关系可以得到其表达式为

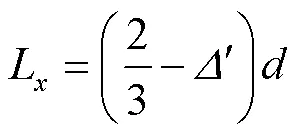
结合式（8），式（5）可以表示为

式中

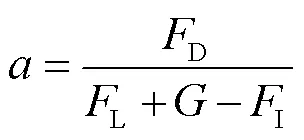
泥沙颗粒处于临界状态时起动概率的取值暂无统一标准，不同的研究者采用不同的起动概率值，总体而言，其变化范围为：0.000 008～0.159[3]。当泥沙颗粒处于临界状态时，无论起动概率如何取值，从式（9）～式（11）可以看出，中间量均为常数，因此结合式（1）～式（4）可以得到

上式中为一常数，可以通过试验数据求得。

层流流速分布满足线性公式[19]，可以表示为

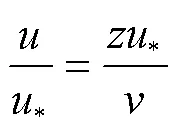
式中为距床面处的水流流速，m/s；*为摩阻流速，m/s；为运动黏滞系数，m/s2。

当有雨滴影响时，公式（13）需加入降雨因素进行修正，这种流速分布规律迄今没有试验来验证，但可以从泥沙运动力学中的含沙水流流速分布规律得到启发。利用Coleman[20]的经典高含沙水流试验数据，绘制了不同泥沙含量下流速分布的变化规律，见图3。从图中可以看出，水流由于挟带泥沙会消耗大量的能量，随着含沙量的增大，流速呈现减小的趋势（该状态下*为定值），在对数坐标系中不同含沙量下的流速数据点总体上为一条直线，说明在泥沙颗粒影响下水流流速分布仍然符合对数分布，因此可以证明含沙水流中水流的流速分布规律在紊流条件下仍然符合对数分布规律。

雨滴落入河流后，会形成雨滴与水流的混合体，其物理图景与含沙水流类似。对雨滴而言，其在落入水流过程中，自身具有一部分能量，进入水流后此部分能量会传递给水流流体，因此，水流的流速也会增大。基于以上分析，假设当有降雨存在时，层流水流流速分布仍然满足线性关系

式中1、2为系数；为降雨强度，mm/h。当降雨量为0时，上式为普通的层流水流流速分布关系式。

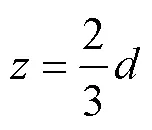
由此可以得到作用力作用点处流速为

式中Re*=*/，表示沙粒雷诺数。

将式（1）～式（4）以及（16）代入式（12），可推导得到

式中表示无因次切应力，定义式为

公式（17）中含有作用力系数D、L，降雨参数S、D、，以及系数1、2，确定这些未知量之后，就可以利用式（17）求解降雨影响下的层流水流泥沙颗粒起动问题。

2 公式参数确定

2.1 作用力系数CD、CL以及常数A的确定

当不受降雨影响时，水流的流速分布规律符合普通的层流水流流速分布关系式，即式（13），此时I以及I都为0，则公式（17）可转换为

从式（19）可以看出，在使用该公式计算降雨影响下的泥沙颗粒起动问题时，不必逐一求解各个变量，只需要求出组合变量D/-L的值即可。拖曳力和上举力系数并不是一个固定值，而是沙粒雷诺数Re*的函数[3,5]，因此组合变量D/L同样是沙粒雷诺数的函数。为了求出组合函数具体的表达式，本研究采用了Shields[21]整理的经典泥沙颗粒起动数据，将其绘制于图4。从图4可以看出，在双对数坐标系中所有数据点大致呈一条直线，这说明组合变量与沙粒雷诺数相关性比较大，二者呈指数关系，可以利用式（20）进行拟合，通过图4中的实测数据与拟合曲线对比，可以看出本文拟合的计算曲线式（20）具有较高的计算精度（2=0.996）。

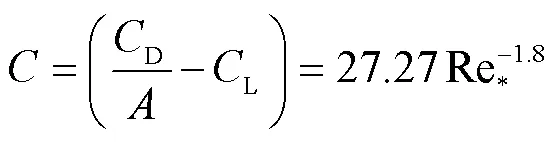
2.2 雨滴粒径DI的确定

雨滴粒径随着降雨强度的变化而变化，但是针对某一降雨强度，其对应的雨滴粒径并不是均匀的[22]。为了确定降雨粒径I，本研究整理了Laws等的经典试验数据[22]，本试验数据共计224组，降雨强度变化范围0.254～152.4 mm/h，基本覆盖了天然降雨的范围[23]。图5显示了雨滴概率密度随雨滴粒径以及降雨强度的变化情况，从图中可以看出，针对某一降雨强度，雨滴粒径D变化范围非常大，其概率密度可以利用如下公式拟合：

图5也绘制了式（21）的计算曲线，其计算结果能够较好地拟合实测数据，表明拟合公式计算精度较高（2=0.998）。

注：该图数据来源为Laws等[22]的经典降雨试验数据。

Note: The data source of this figure is the classical rainfall test data of Laws, et al.

图5 雨滴直径I的概率密度函数

Fig.5 Probability density function of raindrop diameterI

为探讨降雨的作用机理，本研究取降雨强度对应的雨滴平均粒径，其计算公式为

式中为不均匀分布雨滴粒径，m。

将式（21）代入式（22）中，可以得到雨滴的平均粒径表达式

式（23）可以用来计算某一降雨强度对应的雨滴直径，从公式中可以看出雨滴直径随着降雨强度的增大而增大，这一点与天然降雨特征相符。

2.3 其他参数的确定

式（17）中还含有未知参数1、2、I、。其中1、2反映了降雨对于水流结构的影响，可以通过实测数据获得。而I、1-则反映了降雨对于泥沙颗粒作用力的影响，为了便于确定这些变量，将I、1-组合成一个混合变量，其表达式如下：

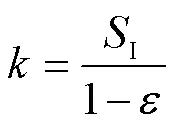
由于I、为由于降雨额外产生的变量，衡量指标为降雨强度，因此，两者的组合变量同样也是降雨强度的函数。为了确定这些变量，本研究采用了Li[10]的降雨影响下层流水流泥沙颗粒起动试验数据。该试验采用水槽13.6 m×0.4 m试验，水槽坡度为2°，床面铺设一层中值粒径为0.74 mm的均匀沙，降雨强度变化范围为0～162 mm/h。经测算，绝大部分雨滴都到达终速，且雨滴均匀分布，接近自然降雨[24-25]。试验中浅层水流的雷诺数Re=39～60，小于明渠及天然河道的下临界雷诺数500，属于层流范畴。在泥沙起动条件方面，为了尽量减小起动水深的测量误差，Li[10]通过求解输沙率为零时的临界水流功率，再除以临界平均流速计算出临界水深，由此得到的泥沙颗粒起动数据更具有可靠性。通过实测数据对比，可以得到：1=0.002，2=0.06。图6点绘了实测的随降雨强度的变化曲线，从图中可以看出，随着降雨强度的增大，系数呈现缓慢增大的趋势，根据其变化规律利用指数及幂函数公式进行拟合，如式（25）所示，决定系数为0.628（图6），公式计算精度比较高。

注：该图数据来源为Li[10]的受降雨影响的泥沙颗粒起动数据。

Note: The data source of this figure is Li's sediment particle incipient data affected by rainfall.

图6 组合变量随降雨强度变化曲线

Fig.6 Variation curve of combined variablewith rainfall intensity

3 受降雨影响的浅水泥沙颗粒起动公式的验证

确定了计算公式的未知参数后，将这些参数式（20）、式（23）、式（25）代入式（17），可以得到

由于式（26）以Re*为变量，根据式（16）和式（18），公式两边都含有待求变量*，需要迭代才能求解，计算起来很不方便。为得出更直接的计算模型，引入无因次泥沙颗粒粒径*，其表达式[26]如下：

式（27）不但将粒径无量纲化，更好地对泥沙颗粒粒径进行量化，使得计算更适用于一般性，更重要的是，它连接了无因次切应力和沙粒雷诺数Re*，能够将式（26）转化成-*类型，不需要迭代即可计算无因次起动切应力值。将式（27）代入到式（26）中可以得到

为了进一步检验本论文建立公式的计算精度，引入误差公式

式中error为相对误差，%；m与s分别表示的测量值和计算值。

图8和表1显示了本文计算公式的误差波动情况，为了进一步比较计算结果，同时将Li[10]和赵春红等[12]的计算结果也绘入了其中。结果显示，本文计算模型拥有最高的计算精度，绝大部分计算结果都落在了10%误差线以内。此外，本文公式的误差波动最小，最小误差为3.9%，最大误差为52.5%，平均误差为14.8%。Li[10]公式计算虽然精度稍差，但是预测效果良好，大部分计算结果控制在20%误差范围以内，其最小误差为6.9%，最大误差为57.4%，平均误差20.5%。计算精度较低的是赵春红等[12]公式，其最小误差为76.1%，最大误差为85.2%，平均已经增大到误差66.6%，这说明赵春红等[12]公式不适用于降雨影响下的层流水流泥沙颗粒起动规律。分析原因，发现赵春红等[12]公式是基于紊流流态下泥沙颗粒受力平衡关系推求得出，其只适用于紊流水流，由于层流与紊流水流作用机制不同[27]，造成赵春红等[12]公式在层流状态下计算精度大大降低。

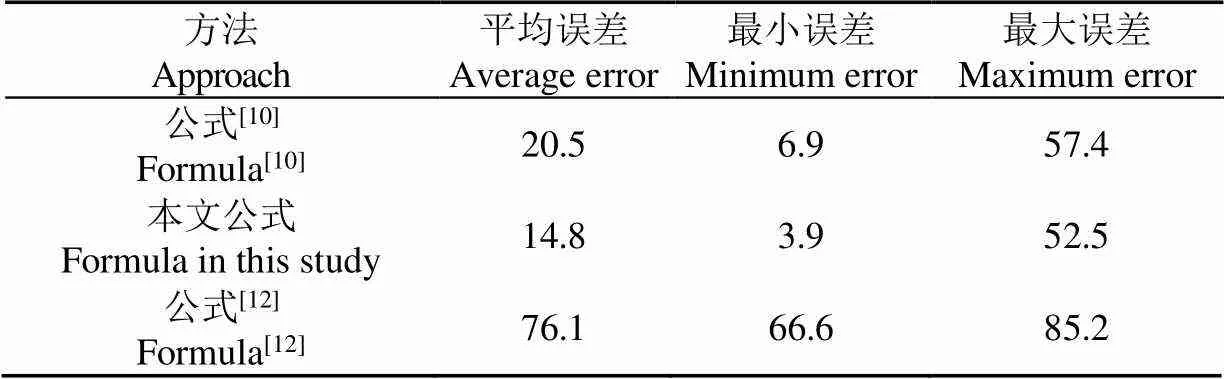
表1 各公式计算θ的误差分析

浅层水流受降雨扰动较大，水流阻力比通常明渠流大，同时雨滴的入射角度会产生更加重要的作用[28-30]。本文先对雨滴影响下的浅层水流泥沙起动做一个初步研究，暂时没有考虑雨滴入射角度的因素，也没有分析对于水流阻力的影响。本研究集中在雨滴垂直落入水流的情形、水流雷诺数Re=/<500的层流状态，工程上使用本公式时也要考虑这些条件的限制。雨滴不同落入角度的影响以及整个水流区的泥沙起动关系式有待于进一步的试验验证和理论研究。

4 结 论

本文假设雨滴落入山区浅水河道后会影响到整个水流区，形成雨滴群与水流混合的流体，类似于孔隙介质的结构，使得泥沙颗粒增加了一个降雨附加力。基于此对受降雨影响下的浅水泥沙颗粒起动规律进行了分析研究，得出了以下结论：

1）结合泥沙颗粒的受力情况，利用泥沙颗粒受力力臂平衡关系式建立了受降雨影响下的层流水流泥沙颗粒起动关系表达式。经过分析发现，由于降雨的影响，会使泥沙颗粒起动时所需的临界切应力变小。

2）将上举力系数、拖曳力系数拟合成组合变量，通过Shields经典泥沙起动数据，发现组合变量与颗粒雷诺数的负1.8次方呈现线性关系，决定系数达0.996，说明得出的受力系数组合变量表达式拟合效果极佳。

3）通过分析降雨试验数据，求出了不同降雨强度下的雨滴直径分布概率密度表达式（决定系数大于0.998），进而推导出雨滴的平均直径表达式，从公式中可以看出雨滴直径随着降雨强度的增大而增大，这一点与天然降雨相符。

4）利用已有研究的试验数据，确定了本文计算公式中的其他待求参数，并引入无因次粒径对公式进行变形整理，将其表示成含无因次粒径的起动切应力公式，使工程应用更加方便。将本文建立的受降雨影响下的层流泥沙起动计算公式与已有研究进行对比，经验证发现：本文的计算模型对有降雨影响的层流水流泥沙颗粒起动切应力的计算精度较高，平均误差为14.8%，最小误差仅为3.9%。

[1] 聂锐华，黄尔，刘兴年，等. 震后崩塌体与滑坡体泥沙起动条件研究[J]. 工程科学与技术，2010，42(5)：180-184.

Nie Ruihua, Huang Er, Liu Xingnian, et al. Study on the sediment incipient motion condition of rock avalanche bodies and landslide bodies after earthquake[J]. Advanced Engineering Sciences, 2010, 42(5): 180-184. (in Chinese with English abstract)

[2] 陈国祥，姚文艺. 降雨对浅层水流阻力的影响[J]. 水科学进展，1996(1)：42-46.

Chen Guoxiang, Yao Wenyi. Effect of rainfall on hydraulic resistance of shallow flow[J]. Advances in Water Science, 1996(1): 42-46. (in Chinese with English abstract)

[3] 钱宁，万兆惠. 泥沙运动力学[M]. 北京：科学出版社，1983.

[4] Vanoni V A. Sedimentation Engineering[M]//ASCE Manuals and Reports on Engineering Practice. Reston: ASCE Press, 2006: 54-61.

[5] Marcelo H G. Sedimentation Engineering Processes, Measurements, Modeling and Practice[M]. Reston: ASCE Press, 2007.

[6] 杨奉广，刘兴年，曹叔尤，等. 希尔兹曲线统一表达式及其在唐家山堰塞湖下游河道冲刷防治中的应用[J]. 四川大学学报：工程科学版，2010，42(5)：175-179.

Yang Fengguang, Liu Xingnian, Cao Shuyou, et al. An uniform formulation of the Shields diagram and its application in the scouring prevention of Tandjiashan barrier lake downstream channel[J]. Journal of Sichuan University: Engineering Science Edition, 2010, 42(5): 175-179. (in Chinese with English abstract)

[7] 褚君达. 无粘性泥沙的起动条件[J]. 水科学进展，1993(1)：37-43.

Chu Junda. Conditions of incipient motion of non-cohesive sediments[J]. Advances in Water Science, 1993(1): 37-43. (in Chinese with English abstract)

[8] 张瑞瑾. 河流泥沙动力学[M]. 北京：中国水利水电出版社，1998.

[9] 聂锐华，刘兴年，曹叔尤，等. 无粘性泥沙起动条件对比研究[J]. 水科学进展，2004(5)：584-587.

Nie Ruihua, Liu Xingnian, Cao Shuyou, et al. Comparison study on incipient motion conditions for cohesionless sediment[J]. Advances in Water Science, 2004(5): 584-587. (in Chinese with English abstract)

[10] Li G. Sediment Transport Capacity of Laminar Overland Flow[D]. Buffalo: State University of New York at Buffalo, 1997: 80.

[11] 韩浩，高建恩，梁改革，等. 降雨条件下坡面径流泥沙起动流速研究[J]. 人民长江，2010，41(12)：49-54.

Han Hao, Gao Jian’en, Liang Gaige, et al. Study on sediment| incipient velocity of slope runoff under rainfall condition[J]. Yangtze River, 2010, 41(12): 49-54. (in Chinese with English abstract)

[12] 赵春红，高建恩，王宏杰，等. 降雨对坡面薄层水流泥沙起动的影响[J]. 应用基础与工程科学学报，2013，21(6)：1057-1069.

Zhao Chunhong, Gao Jianen, Wang Hongjie, et al. Effect of rainfall on sediment incipient motion of overland flow[J]. Journal of Basic Science and Engineering, 2013, 21(6): 1057-1069. (in Chinese with English abstract)

[13] Yang F G, Liu X N, Cao S Y, et al. Study on bed load transport for uniform sediment in laminar flow[J]. Science China Technological Sciences, 2010, 53(9): 2414-2422.

[14] Bear J. Dynamics of Fluids in Porous Media[M]. New York:Dover Publications, 1972.

[15] Cheng N S, Qiao C K, Chen X W, et al. Application of pseudo-fluid approximation to evaluation of flow velocity through gravel beds[J]. Power Technology, 2014, 260: 15-21.

[16] 薛禹群. 地下水动力学[M]. 北京：地质出版社，1997.

[17] Yalin M S. Mechanics of Sediment Transport[M]. Oxford: Pergamon Press, 1972.

[18] 杨奉广，刘兴年，黄尔，等. 唐家山堰塞湖下游河床泥沙起动流速研究[J]. 四川大学学报：工程科学版，2009，41(3)：84-89.

Yang Fengguang, Liu Xingnian, Huang Er, et al. Study on the Incipient Velocity of Tangjiashan Barrier Lake Downstream Area Sediment[J]. Journal of Sichuan University: Engineering Science Edition, 2009, 41(3): 84-89. (in Chinese with English abstract)

[19] Nakagawa H, Nezu I. Turbulence in Open-Channel Flows[J]. Journal of Hydraulic Engineering, 1993, 120(10): 1235-1237.

[20] Coleman N L. Effects of suspended sediment on the open channel velocity distribution[J]. Water Resources Research, 1986, 22(10): 1377-1384.

[21] Shields A F. Anwendung der Aehnlichkeitsmechanik undder Turbulenzforschung auf die Geschiebebewegung[R]. Berlin: Preussische Versuchsanstalt fur Wasserbauund Schiffbau: 1936.

[22] Laws J, Parsons D. The relationship of raindrop size to intensity[J]. Transactions American Geophysical Union, 1943, 24(2): 452-460.

[23] 张晶玲，周丽丽，马仁明，等. 天然降雨条件下横垄与顺垄坡面产流产沙过程[J]. 水土保持学报，2017，31(5)：114-119.

Zhang Jingling, Zhou Lili, Ma Renming, et al. Runoff and sediment yield process on longitudinal and cross ridge slopes under natural rainfall[J]. Journal of Soil and Water Conservation, 2017, 31(5): 114-119. (in Chinese with English abstract)

[24] 柯奇画，张科利. 人工降雨模拟试验的相似性和应用性探究[J]. 水土保持学报，2018，32(3)：16-20.

Ke Qihua, Zhang Keli. An exploration on t he similarity and applicability of simulated rainfall experiments[J]. Journal of Soil and Water Conservation, 2018, 32(3): 16-20. (in Chinese with English abstract)

[25] 范荣生，李占斌. 用于降雨侵蚀的人工模拟降雨装置实验研究[J]. 水土保持学报，1991(2)：38-45.

Fan Rongsheng, Li Zhanbin. Artifical rainfall device for soil erosion study[J]. Journal of Soil and Water Conservation, 1991(2): 38-45. (in Chinese with English abstract)

[26] 马志伟，杨奉广，刘兴年，等. 对Vanoni希尔兹曲线辅助线方法的研究[J]. 工程科学与技术，2017，49(增刊2)：62-66.

Ma Zhiwei, Yang Fengguang, Liu Xingnian, et al. Revised Vanoni auxiliary line method for Shields diagram[J]. Advanced Engineering Sciences, 2017, 49(S2): 62-66. (in Chinese with English abstract)

[27] 李寿千，陆永军，左利钦，等. 单向流边界层泥沙起动规律[J]. 水科学进展，2013，24(6)：821-829.

Li Shouqian, Lu Yongjun, Zuo Liqin, et al. Incipient sediment motion in steady boundary layers[J]. Advances in Water Science, 2013, 24(6): 821-829. (in Chinese with English abstract)

[28] 姚文艺. 坡面流阻力规律试验研究[J]. 泥沙研究，1996(1)：74-82.

Yao Wenyi. Experiment study on hydraulic resistance laws of overland sheet flow[J]. Journal of Sediment Research, 1996(1): 74-82. (in Chinese with English abstract)

[29] 王俊杰，张宽地，杨苗，等. 雨强和糙度对坡面薄层流水动力学特性的影响[J]. 农业工程学报，2017，33(9)：147-154.

Wang Junjie, Zhang Kuandi, Yang Miao, et al. Influence of rainfall and roughness on hydrodynamics characteristics of overland flow[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(9): 147-154. (in Chinese with English abstract)

[30] 杨坪坪，王云琦，张会兰，等. 降雨强度和单宽流量与地表粗糙度交互作用下坡面流阻力特征[J]. 农业工程学报，2018，34(6)：145-151.

Yang Pingping, Wang Yunqi, Zhang Huilan, et al. Characteristics of overland flow resistance under interaction of rainfall intensity and unit discharge and surface roughness[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(6): 145-151. (in Chinese with English abstract)

Incipient law of sediment particles in shallow water affected by rainfall

Xiao Ke, Yang Fengguang※, Nie Ruihua, Huang Er, Wang Xiekang, Liu Xingnian, Peng Qing’e

(,,610065,)

Sediment transport is a key link to the river flow in mountainous areas under rainfall conditions. Mountain river flow is usually considered to be laminar, because of the shallow depth and large slope. This study aims to investigate the influence of rainfall on the incipient motion of uniform sediment in laminar open channel flows. A mathematical model was also established for the incipient shear stress of sediment particles under the rainfall when the rainfall fell into the main flows with terminal velocity. Assuming that the rainfall remained the unchanged shapes in a short period, a scenario was developed, particularly when the rainfall drop particles settled in stationary water. As such, the water was assumed as the transport in the porous media with relative velocity. Both scenarios were considered equivalent, in terms of grain size, porosity, and drag forces. A critical shear stress model was derived using the conception of flow transportation in the porous media, where the forces were analyzed when acting on the uniform sediment particles. The analysis results showed that there was little influence of rainfall on the velocity, where the linear velocity profile was still applied. The coefficients of lift and drag forces were determined with the measured incipient shear stress data without disturbance of the rainfall. It was found that both of them were a function of shear Reynolds number. The combined variables were fitted using two force coefficients, thereby obtaining a linear relationship with shear Reynolds number and the power of -1.8(2=0.996). 8 different rainfall intensities varying from 0.254 to 152.4 mm/h were selected, when fitting to the 224 original measured data, to finally develop the probability density function of raindrop diameters for given rainfall intensity (2=0.998). Therefore, the average diameter value used in the present study was obtained by integration. The remaining parameters of the model were obtained to compare the present model with Garry Li experimental data. It was found that the critical shear velocity was reduced for the presence of the rainfall. The experiments were performed on a flume with a test section of 3.6 m long and 0.4 m wide. The flume bed was covered with sediments using the median diameters of 0.74 mm, and the inclined angle at slopes of 2.0°. The simulated rainfall was provided by three nozzles located 3.6 m above the center of the flume connected to the water mains, and the rainfall intensity varied from 0 to 162 mm/h. Reynolds number of shallow flow in the experiment was 39-60, smaller than the lower critical Reynolds number of the natural river channels. Comparison with Garry Li measured data, the computation model could more accurately predict the critical shear stress for the laminar flow with rainfall disturbance. To verify the accuracy of the model, the obtained values were compared with the predictions of Li formula and Zhao et al. formula. Specifically, the accuracy of the model was the highest, where the average error was 14.8% and the minimum error was only 3.9%. A mathematical model of incipient shear stress can be used for the sediment particles, where the influence of rainfall can provide theoretical support to the prevention and control of water and sediment disasters in mountainous areas.

rainfall; shear stress; sediment particle; friction velocity; relative exposure

肖克，杨奉广，聂锐华，等. 受降雨影响的浅水泥沙颗粒起动规律[J]. 农业工程学报，2021，37(13)：121-127.

10.11975/j.issn.1002-6819.2021.13.014 http://www.tcsae.org

Xiao Ke, Yang Fengguang, Nie Ruihua, et al. Incipient law of sediment particles in shallow water affected by rainfall[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(13): 121-127. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.13.014 http://www.tcsae.org

2021-04-23

2021-06-09

国家自然科学基金资助项目（51979180，U20A20319）

肖克，研究方向为水力学及河流动力学。Email：18856332202@163.com

杨奉广，博士，副研究员，研究方向为水力学及河流动力学。Email：yangfengguang@scu.edu.cn

10.11975/j.issn.1002-6819.2021.13.014

TV142.1

A

1002-6819(2021)-13-0121-07