干旱区引水灌区灌溉退水计算方法

介飞龙，费良军，李 山，朱红艳，郝 琨，刘利华

干旱区引水灌区灌溉退水计算方法

介飞龙，费良军※，李 山，朱红艳，郝 琨，刘利华

（西安理工大学西北旱区生态水利国家重点实验室，西安 710048）

准确计算干旱地区灌区退（回归）水，对水资源高效利用具有重要意义。针对中国西北干旱地区大量引水灌区的特点，该研究结合退水单位线和“水桶模型”（根系层的水均衡模型）建立了灌溉退水计算模型，并将该模型应用于甘肃省景电灌区（黄河流域部分）的退水计算，结果表明：灌区退水量计算值与监测值拟合良好，模型率定期和验证期决定系数分别为0.82和0.71，模型可靠。2000年至2019年深层渗漏量和退水量的分析结果表明：年深层渗漏量与净灌溉和有效降雨的总量呈显著正相关，相关系数=0.718（<0.01）；月深层渗漏量受灌区作物生长期的影响显著，69.6%的深层渗漏在冬灌（10－11月）期间产生；年深层渗漏系数与年深层渗漏量呈显著正相关（=0.944，<0.01）；月深层渗漏系数在作物主要生长期（4－9月）小于0.4，非生长期（11月至次年2月）大于0.8；年退水量与年深层渗漏量呈显著正相关（=0.716，<0.01）；月退水量与月深层渗漏量相关性较差，原因是灌溉退水存在明显的滞后性；研究区退水单位线表明灌溉退水滞后峰值在2个月左右，但深层渗漏对退水的影响可达24个月左右。退水单位线的参数具有明确的物理意义且易于确定，针对灌溉退水具有明显滞后性的干旱地区，该方法能够有效计算灌区灌溉退水量，可为灌区水资源管理和决策提供科学支撑。

地下水；入渗；灌溉；引水；退水单位线；干旱区

0 引 言

干旱地区大规模的引水灌溉显著地影响区域地表及地下的水文过程[1-2]，随着农业用水需求的增加，灌区面临着日益严重的缺水问题。灌溉退水可以被定义为未被作物利用的引水或降水返回到其源头或其他地表水体的水量[3]，其重复利用可有效提高灌溉水利用效率[4]，因此准确计算灌区灌溉退水对灌区水资源管理具有重要意义[5]。

针对干旱区引水灌区的特点，本文所研究的灌溉退水指降雨或引水通过深层渗漏和地下径流的方式进入排水渠或河流的水量。目前，统计和经验方法被广泛用于计算灌区灌溉退水。Dewandel等[6]利用水动力学模型建立了井灌区退水系数计算方法，并分别计算了灌区中不同作物种植区的退水系数。Mohan等[3]建立了灌溉退水量与有效降水、灌水量、作物耗水量和渗漏损失间的回归树模型。Li等[7]采用支持向量机法计算干旱地区灌溉退水量，并实现了灌区水土资源的优化。由于干旱地区包气带厚度较大，退水存在显著的滞后性[8]，采用统计和经验方法计算退水量可能会产生显著的误差。因此，在干旱地区退水研究中考虑滞后性非常重要[9-10]。除统计和经验方法外，SWAP[11]、SWAT[12]、HYDRUS[13-14]等模型也被用于灌区退水计算。虽然水文模型能够考虑土壤水渗流和地下水之间的相互作用，并在一定程度上考虑灌溉退水的滞后性，但目前大多数水文模型侧重于产汇流机制的研究，在地下水与地表水之间的水量交换以及非饱和带土壤水与地下水之间的转换方面进行了较多的简化处理[15]。此外，水文模型所需要的资料和数据较多且精度要求高，参数的确定较复杂，同时还存在异参同效的问题[16]，这些瓶颈一定程度上限制了水文模型在资料短缺的干旱地区的灌溉退水计算。为了实现干旱地区农业水资源的高效利用，亟需一种简单高效的方法计算干旱区引水灌区的灌溉退水量。

单位线法基于倍比和叠加原理，计算由净雨汇流形成的流域断面出口流量，在洪水预报中应用较广。Nash[17]将地面汇流过程视为一系列串联水库的调蓄过程，并基于线性系统理论得到瞬时单位线方程。单位线实质上是净雨的滞后分配曲线，对于干旱区引水灌区而言，灌溉退水过程可视为包气带和含水层对深层渗漏水的调蓄过程，因此Nash线性水库理论同样适用灌溉退水计算。

为研究干旱区引水灌区的退水变化规律及影响因素，本研究提出了退水单位线的概念，并基于Nash线性水库理论得到退水单位线方程。利用水均衡模型计算灌区深层渗漏量，结合退水单位线和倍比叠加原理构建干旱区引水灌区的灌溉退水计算模型。以甘肃省景电灌区（黄河流域部分）为例，在验证退水单位线模型可靠性的基础上，从年尺度和月尺度上分析研究区深层渗漏量和灌溉退水量之间的联系及其影响因素，揭示灌区退水变化规律，以期为干旱地区引水灌区提供了一种简单有效的灌溉退水计算方法，并为灌区水资源管理与高效利用提供科学指导。

1 研究内容与研究方法

1.1 灌溉退水计算模型

由于干旱地区的地下水埋深较深，灌溉退水往往存在滞后性。图1是干旱地区引水灌区灌溉退水过程示意图，本文将灌溉退水过程简化为“渗漏”和“回归”两个阶段。在“渗漏”阶段，降雨和灌溉水入渗至作物根系层，一部分水以蒸发蒸腾的方式消耗，一部分储存于根系层的包气带中，当根系层包气带水到达最大持水能力后，根系层底部便产生深层渗漏；在“退水”阶段，深层渗漏水经过包气带入渗至含水层补给地下水，再通过地下径流形成河道退水。

深层渗漏量可利用“水桶模型[18]”计算，该模型将根系层看作可蓄水的“水桶”，当根系层的总水量超过了最大容水量时则产生深层渗漏，模型可表示为

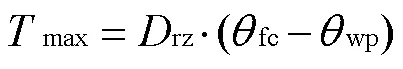
式中DP()表示第天的深层渗漏量，mm；max表示根系层最大容水量，mm；rz表示根系层平均深度，mm；fc和wp分别表示根系层田间持水量和凋萎含水率，cm3/cm3；()表示第天根系层的总水量，mm；计算()需要考虑不同情况，当第-1天产生的深层渗漏大于0和等于0时，分别根据式（3）和式（4）计算()：

式中I()表示第天的净灌溉水量，mm，可根据引水量和渠系利用系数计算，即N=∙；e()表示第天的有效降水量，mm；ETc()表示第天的作物需水量，mm。e和ETc可分别采用有效降雨量的经验公式和单作物系数法[19]计算：

式中a()表示第天的实际降雨量，mm；c为作物系数；ET0表示参考作物需水量，mm，可根据FAO 56推荐的Penman-Monteith公式[20]计算：

式中n为作物表面净辐射量，MJ/(m2∙d)；为土壤热通量，MJ/(m2∙d)；为2 m高处的平均气温，℃；2为2 m高处的风速，m/s；s为饱和水气压，kPa；a为实际水气压，kPa；为饱和水气压与温度曲线的斜率，kPa/℃；为干湿表常数，kPa/℃。

在“回归”阶段，深层渗漏水转化为退水存在滞后性，可通过退水单位线（Unit Return-Flow-Graph，URFG）描述退水滞后现象。单位线法计算地面汇流遵循的基本假设是：不同强度净雨所形成的断面出口流量过程线的形状相同，实际上就是将不同强度净雨的汇流问题视为一个线性可叠加过程[21]。对于干旱区引水灌区，退水过程与地面汇流过程具有相似性，深层渗漏可视作单位线中的“净雨”，包气带和含水层的调蓄过程可视为“地面汇流过程”，因此将灌溉退水过程视为线性可叠加系统，遵循倍比和叠加假设。

据此，本文将退水单位线定义为：单位时段内给定流域上、时空分布均匀的深层渗漏水所形成的退水权重曲线。单位时段可依据滞后时间尺度确定，干旱地区灌区退水滞后时长一般以月计算，故本文取月作为单位时段，并在计算时将相关的日尺度计算结果转化为月尺度。与单位线法相同，退水单位线同样遵循3个假设：1）单位时段内深层渗漏量不同，但所形成的退水过程线的总历时不变；2）单位时段内倍单位深层渗漏量所形成的退水量为退水单位线的倍；3）各单位时段深层渗漏量所产生的退水过程不相干扰，总退水量等于各单位时段深层渗漏量所形成的退水量之和。根据倍比和叠加原理，多时段深层渗漏量产生的总退水过程可表示为

式中RF()表示第时段的总灌溉退水量，m3；DP()表示第时段产生的深层渗漏量，m3；−表示灌溉退水相对于深层渗漏的滞后时段数；(−)表示退水单位线的权重系数，即第时段深层渗漏量在第时段产生的灌溉退水所占比重。式（8）中的DP可由式（1）计算得到，因此，只需要确定退水单位线即可计算出退水时间序列。

1.2 退水单位线原理

Nash[17]假设任何流域都可被视为一系列具有调蓄作用的串联线性水库，并通过线性系统理论得到瞬时单位线方程。包气带和含水层同样具有调蓄作用，可视为串联线性水库。参照Nash瞬时单位线理论，本文引入瞬时退水单位线的概念，即流域上均匀分布、历时趋于0、强度无限大、总量为1的单位深层渗漏量所形成的退水过程。图2为Nash线性水库模型，假设第个水库的蓄水量W（m3/d）与出流量Q（m3/d）之间为线性关系，则有

式中表示第个水库的蓄泄系数。

注：0为第1个水库的入流量，m3·d-1；Q为第个水库的出流量，m3·d-1；为时间，d；q为第个水库的单位线的流量，m3·d-1。

Note:0is inflow of the first reservoir, m3·d-1;Qis outflow of thethreservoir, m3·d-1;is time, d;qis hydrograph of thethreservoir, m3·d-1.

图2 Nash线性水库模型[17]

Fig.2 Nash’s linear reservoir model

第个水库的水量平衡方程可表示为

联立式（9）和式（10）求解得第个水库的出流量与第－1个水库出流量之间的关系：

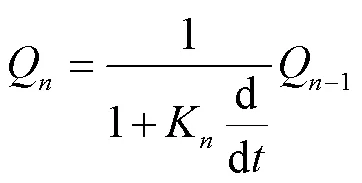
假设个线性水库的调蓄作用是相同的，蓄泄系数1=2=3=…=K，则根据式（11）可得到第个水库的出流量为

式中0为第1个水库的入流量，根据瞬时退水单位线的定义，当0为瞬时单位脉时，即0=()，则出流过程Q即表示瞬时退水单位线。利用Laplace积分变换求解式（12）即可得到瞬时退水单位线方程为

式中()表示的Gamma函数。0()是瞬时退水单位线在时刻的出流量。式（13）实质上是Nash瞬时单位线方程在瞬时退水单位线中的应用，尽管两者的数学方程相同，但物理意义不同。

由于瞬时退水单位线是一个脉冲函数的响应过程，在计算退水时无法使用倍比和叠加原理。因此，需通过S曲线将瞬时退水单位线转化为退水单位线。S曲线可以看作是强度为1的连续深层渗漏形成的退水过程，即瞬时退水单位线的积分曲线，其数学方程为

式中表示下不完全Gamma函数，可表示为

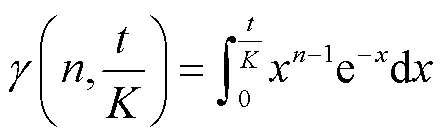
S曲线是一条单调递增曲线，值域在0到1之间。将()曲线向右平移1个时段，得到一条延迟的曲线(−1)。在各个时段上，S曲线与S(−1)曲线之间的面积就是退水单位线的值。使用积分方法求取各时段的面积，则退水单位线可表示为

应当注意(−1)曲线的定义域是∈[1,+∞)，因此当<1时，式（16）中的(−1)=0。将式（15）带入式（16）得到退水单位线的积分表达式

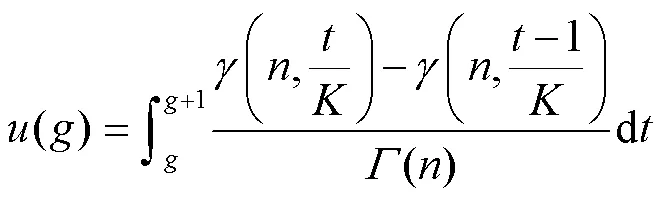
式（17）是一个复杂函数的积分，可采用差分方法求解近似面积，从而得到其近似解为

式（18）中的Gamma函数和下不完全Gamma函数可查Gamma函数表或通过MATLAB R2017软件计算得到。

联立式（8）和式（18）得到退水计算模型

式（19）中的DP可通过式（1）计算，因此只需确定参数和就可以计算退水时间序列。

1.3 退水单位线参数确定方法

参数和可用试算法得到。根据最小二乘法原理，RF观测值与计算值的残差函数可表示为

式中n和K是最小二乘法计算过程中参数和的序号，即n为第个，K为第个；RFobs和RFcal分别表示第时段灌溉退水的观测值和计算值，m3；表示计算时段总数。最小二乘法确定最优参数是通过最小化残差函数进行的，当和满足下式时就是给定观测数据条件下的最优参数：

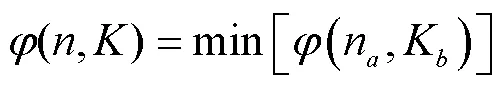
2 案例分析

2.1 研究区概况

景电灌区位于甘肃省中部的景泰县和古浪县（图3），属于典型的干旱区农业引水灌区，灌溉方式为电力灌溉，水源全部来自于黄河引水，区内多年平均降水量为186 mm，多年平均水面蒸发强度2 123 mm，水资源极其匮乏。研究区为景电灌区东部隶属于黄河流域的部分，总面积为351.3 km2，其中灌溉面积为235.4 km2。区内地表径流和地下水源都很匮乏，除降雨外，区内的地表水资源全部来自黄河引水，地下水资源可利用量仅0.42亿m3。研究区地下水由西向东径流，地下水埋深1.2～54.6 m，地下水主要补给来源为灌溉和降雨产生的深层渗漏水，排泄方式为沟道退水。由于地下水补给条件不充沛，所以地下水量较少，埋藏较深，且水质较差。研究区根系层的土壤质地以砂壤土为主，包气带和含水层以粉土、粉壤土、砂壤土、砂和砾石为主。

2.2 数据来源

计算参考作物需水量所需要的气象资料来自于景泰县国家气象站和中国气象局，数据包括2000－2019年的日降水量（mm），平均气温（℃）、风速（m/s）、相对湿度（%）和日照时数（h）。计算作物需水量所需要的数据由景电管理局提供，包括2000－2019年的作物种植面积、类型、种植结构。2000－2019年的灌区引水量数据来自景电管理局，灌区多年平均渠系利用系数为0.724。灌溉退水监测数据由研究区6组量水堰监测得到。灌区主要作物类型包括春小麦、大麦、玉米、大豆、胡麻、洋芋、瓜类、枸杞和林果，共9类。作物系数根据研究区的气候资料对FAO推荐的作物系数进行修正，采用文献[7]的研究成果（表1）。由于灌区作物种植类型复杂多样，不同生育期的根系深度也有所不同，本文取根系深度的加权平均值0.3 m。灌区土壤参数根据室内试验测定，田间持水量取0.25，凋萎含水率一般认为是压力水头在−155 m时的体积含水率[22]，通过土壤水分特征曲线确定为0.07。

图件绘制和数据处理使用ArcGIS 10.2和Microsoft 365 (Excel和VBA)软件，相关系数使用SPSS 25确定。

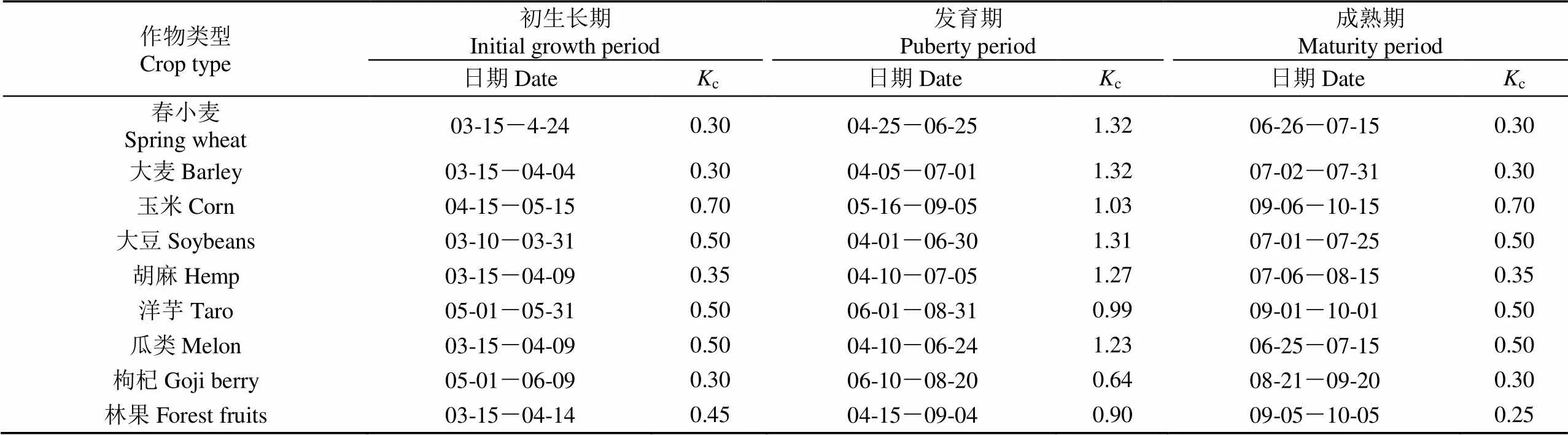
表1 研究区作物生长期及作物系数[7]

注：c为作物系数。

Note:cis crop coefficient.

2.3 作物需水量计算与分析

图4a为作物需水量的计算结果。受到气候因素的不确定性的影响，ETc在20 a间呈无规律的变化，但与ET0变化趋势基本一致。由图4b可以看出，月尺度ET0和ETc呈单峰变化，峰值分别在6月和7月。ET0在4－8月较大（>110 mm），而ETc仅5－6月较大，其原因是灌区作物的生长期集中在5－6月，在此期间耗水量较大。而4月和7－8月ETc相对较小，这是由于4月是春小麦、玉米和林果的初生长期，而7－8月是春小麦、大麦、大豆、胡麻的成熟期，此期间耗水量相对较小。

2.4 深层渗漏的计算与分析

图5a为年深层渗漏量、有效降雨量和净灌溉量的计算结果，可以看出年深层渗漏量与有效降雨和净灌溉总量（N+e）的变化趋势基本一致，二者的相关系数为0.718 （<0.01）。图5b表明月深层渗漏量在年内呈双峰变化，大小峰值出现在冬灌（10－11月）和秋灌（7－8月）期间，分别占全年总渗漏量的69.6%和21.4%。小峰值（秋灌渗漏量）是由于7－8月的净灌溉水量未完全被作物消耗，剩余水量除填充根系层的缺水量以外，均转化为深层渗漏。而大峰值（冬灌渗漏量）产生的原因是冬灌期间作物耗水量几乎为0，大量的冬灌溉水便形成深层渗漏。

由图6a可看出研究区年深层渗漏系数（深层渗漏量占净灌溉水和有效降雨总量的比例）在0.14～0.32之间，年深层渗漏量与深层渗漏系数呈线性正相关关系，相关系数为0.944（<0.01）。由图6b可以看出月深层渗漏系数在年内差异较大，11月至次年2月均大于0.8，而在4－9月均小于0.4。原因是4－9月是灌区作物的主要生长期，在此期间大部分土壤水被作物消耗，因此深层渗漏系数较小；而11月至次年2月几乎不产生作物消耗，大量的灌溉水和降水得以形成深层渗漏，因而深层渗漏系数较大。

2.5 灌溉退水计算与分析

共计38个月的退水监测数据用于退水单位线的参数率定及验证，其中2016年1－12月退水监测数据由景电管理局提供，2017年11月至2019年12月的监测数据由研究区的量水堰监测得到。图7为灌溉退水计算值与监测值的拟合结果，可以看出计算值与监测值的变化趋势一致，参数识别期和验证期2分别为0.82和0.71，拟合良好，模型可靠。根据拟合结果确定研究区退水单位线的参数和分别为1.28和5.82，退水单位线方程为

考虑到滞后时间在24个月以内的深层渗漏量对退水存在一定影响，故从2002年起计算灌溉退水量。图8a为2002－2019年的灌溉退水量的计算结果。年退水量在17.45至42.67×106m3之间变化，年退水量与年深层渗漏变化趋势基本一致，相关系数为0.716（<0.01）。图8b是月平均灌溉退水量计算结果。月退水量峰值出现在12月份，晚于深层渗漏量在11月和8月的大小峰值，表明月灌溉退水量存在明显的滞后效应。

表2为灌溉退水量与作物需水量、深层渗漏量、净灌溉量和有效降雨总量的相关系数计算结果。年退水量与年深层渗漏量和N+e的相关系数分别为0.716（<0.01）和0.636（<0.01），表明年尺度上影响灌溉退水的主要因素是深层渗漏量和N+e，作物需水量影响较小。年退水量与深层渗漏的相关系数稍大于与N+e的相关系数，原因是年深层渗漏的大小直接影响灌溉退水量，而N+e是深层渗漏水的主要影响因素，而间接影响了灌溉退水的大小。月退水量与深层渗漏量相关系数为−0.003，与作物需水量和N+e相关系数分别为−0.689（<0.05）和−0.740（<0.01）。原因是受到灌溉退水的滞后影响，月退水量与月深层渗漏的变化趋势不一致导致了两者的相关系数接近于0。而月退水量与N+e呈显著负相关的原因是，月退水量受到滞后影响退水峰值出现在12月，与N+e峰值（6月）相差半年，从而导致月退水量与N+e在年内变化趋势恰好相反，二者呈现出显著负相关关系。

从不同时间尺度来看，灌溉退水的影响因素不尽相同。年退水量受到滞后影响相对较小，与深层渗漏具有较强的相关性，灌溉退水量的大小长期将由深层渗漏量决定。而月退水量受滞后影响较大，一方面体现在深层渗漏峰值的滞后，另一方面体现在灌溉退水的波动远不及深层渗漏波动差异大，在包气带和含水层的调蓄作用下灌溉退水峰值坦化严重。从相关系数上来看，影响年退水量的直接因素是年深层渗漏量，间接因素是N+e；月退水量受滞后影响与各因素的相关关系较差或呈负相关关系。

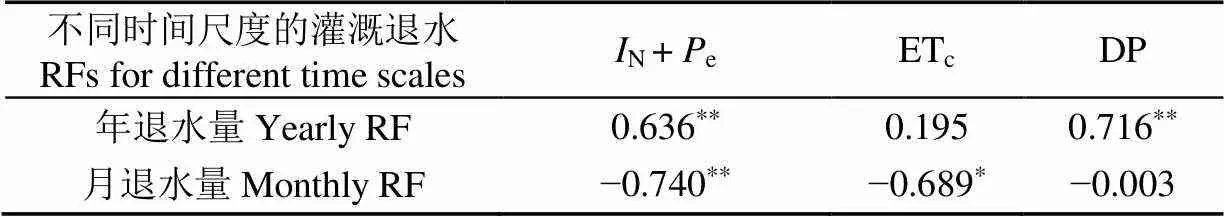
表2 灌溉退水（RF）与作物需水量（ETc）、深层渗漏量（DP）、净灌溉量和有效降雨量总量（IN+Pe）的相关系数

注：**表示在0.01水平显著相关；*表示在0.05水平显著相关。

Note:**shows a significant correlation at the 0.01 level;*shows a significant correlation at the 0.05 level.

3 讨 论

中国西北干旱地区存在许多引水灌溉工程，既保证了当地农业发展，也改善了灌区及周边生态环境[23]。景电灌区作为典型的引水灌区，灌溉退水是该地区重要的农业水资源之一，准确预测灌区灌溉退水能有效提高水资源利用效率。而强烈的人类活动改变了研究区的自然水循环过程，“引水-灌溉-回归”的水循环过程在区内发挥了主导作用[24]。基于这一水循环过程，本文建立了退水单位线模型。与传统的多元回归方法[1]相比，退水单位线能充分反应退水滞后过程，模型适用于滞后效应明显的干旱地区。此外，与SWAT等水文模型相比，退水单位线模型所需要的参数更少且易于确定，实用性相对更好。

干旱地区地下水补给（潜在退水量）的滞后性不容忽视[25]，Lu等[26]证明在地下水埋深较小的沿海平原，滞后时间一般不超过1～2 d，但在地下水埋深较大（>10 m）的地区，滞后时间将达到18～35 d。景电灌区的地下水埋深在1.2～54.6 m之间，由图7a可以看出灌区退水滞后时间峰值出现在2个月后，但深层渗漏对退水的影响可达20个月以上。对于地下水位埋藏更大的地区，滞后时间甚至可以达到几年到几十年不等[27]。Jafari等[5]认为土壤质地也是影响滞后时间的主要因素，粗粒土壤中的大孔隙能减弱灌溉退水的滞后性。景电灌区北部接壤腾格里沙漠，土壤质地多为砂性土，在一定程度上减小了退水滞后时间，但由于灌区包气带厚度较大，因此退水滞后效应依然明显。

深层渗漏是地下水（潜在退水量）的重要补给来源[4]。Fisher等[28]研究发现几乎所有深层渗漏都发生在灌溉季节，这与本文的研究结果相同。不同的是，景电灌区的深层渗漏量在年内分布极不均匀，69.6%的深层渗漏产生在非作物生长期的冬灌（10－11月）期间，这说明了作物生长期对月深层渗漏量影响较大。与深层渗漏量相比，年退水量和月退水量的变化都相对较平缓，其原因是，在包气带和含水层的调蓄作用下，相对集中的深层渗漏水被分散至不同时段形成灌溉退水。Jafari等[5]研究发现，当灌溉退水滞后时间为3个月时，年潜在退水量和年深层渗漏量的相关系数为0.99（<0.01），大于景电灌区的0.716（<0.01）。由于景电灌区退水滞后历时较长，由退水单位线可以看出深层渗漏量对退水的影响可达到24个月左右，本年度的灌溉退水在一定程度上受上年度深层渗漏的影响，因此景电灌区年退水量与年深层渗漏量的相关系数稍小，但相关性依然显著。综上所述，退水与深层渗漏之间虽联系紧密，但在干旱地区，灌溉退水过程受到明显的滞后影响。

4 结 论

1）基于水均衡模型和退水单位线建立了适用于干旱地区引水灌区的灌溉退水计算模型；案例分析的结果表明，退水单位线模型在参数率定期和验证期的决定系数2分别为0.82和0.71，模型可靠。

2）研究区年深层渗漏量的主要影响因素是净灌溉和有效降雨的总量，相关系数为0.718（<0.01）；月深层渗漏量受作物生长期的影响较大，69.6%的深层渗漏产生在非作物生长期的冬灌期间。

3）研究区年退水量的主要影响因素是年深层渗漏量，相关系数为0.716（<0.01）；月退水量与月深层渗漏量相关性较差，原因是灌溉退水存在明显的滞后性；由退水单位线可知，灌溉退水滞后峰值在2个月左右，但深层渗漏对退水的影响可达24个月左右。干旱地区灌溉退水滞后问题不容忽视。

[1] Loheide S P, Butler J J, Gorelick S M. Estimation of groundwater consumption by phreatophytes using diurnal water table fluctuations: A saturated-unsaturated flow assessment[J]. Water Resources Research, 2005, 41(7): 1-14.

[2] Leng G Y, Huang M Y, Tang Q H, et al. Modeling the effects of groundwater-fed irrigation on terrestrial hydrology over the conterminous united states[J]. Journal of Hydrometeorology, 2014, 15(3): 957-972.

[3] Mohan S, Vijayalakshmi D P. Prediction of irrigation return flows through a hierarchical modeling approach[J]. Agricultural Water Management, 2009, 96(2): 233-242.

[4] Simons G, Bastiaanssen W, Immerzeel W W. Water reuse in river basins with multiple users: A literature review[J]. Journal of Hydrology, 2015, 522: 558-571.

[5] Jafari H, Raeisi E, Zare M, et al. Time series analysis of irrigation return flow in a semi-arid agricultural region, Iran[J]. Archives of Agronomy and Soil Science, 2012, 58(6): 673-689.

[6] Dewandel B, Gandolfi J M, De Condappa D, et al. An efficient methodology for estimating irrigation return flow coefficients of irrigated crops at watershed and seasonal scale[J]. Hydrological Processes, 2010, 22(11): 1700-1712.

[7] Li J S, Fei L J, Li S, et al. The influence of optimized allocation of agricultural water and soil resources on irrigation and drainage in the Jingdian Irrigation District, China[J]. Irrigation Science, 2020, 38(1): 37-47.

[8] De Vries J J, Simmers I. Groundwater recharge: An overview of process and challenges[J]. Hydrogeology Journal, 2002, 10(1): 5-17.

[9] Turkeltaub T, Dahan O, Kurtzman D. Investigation of groundwater recharge under agricultural fields using transient deep vadose zone data[J]. Vadose Zone Journal, 2014, 13(4): 963-971.

[10] Hubbell J M, Nicholl M J, Sisson J B, et al. Application of a darcian approach to estimate liquid flux in a deep vadose zone[J]. Vadose Zone Journal, 2004, 3(2): 560-569.

[11] Anuraga T S, Ruiz L, Kumar M S M, et al. Estimating groundwater recharge using land use and soil data: A case study in South India[J]. Agricultural Water Management, 2006, 84(1/2): 65-76.

[12] Awan U K, Ismaeel A. A new technique to map groundwater recharge in irrigated areas using a SWAT model under changing climate[J]. Journal of Hydrology, 2014, 519: 1368-1382.

[13] Poch-Massegú R, Jiménez-Martínez J, Wallis K J, et al. Irrigation return flow and nitrate leaching under different crops and irrigation methods in Western Mediterranean weather conditions[J]. Agricultural Water Management, 2014, 134: 1-13.

[14] Jiménez-Martínez J, Skaggs T H, Van Genuchten M T, et al. A root zone modelling approach to estimating groundwater recharge from irrigated areas[J]. Journal of Hydrology, 2009, 367(1/2): 138-149.

[15] 贾仰文，王浩. 分布式流域水文模型原理与实践[M]. 北京：中国水利水电出版社，2005.

[16] 黄晓荣. 灌区水循环模拟研究进展[J]. 水资源与水工程学报，2010，21(2)：53-55.

Huang Xiaorong. Research prospect of water cycle simulation in irrigation district[J]. Journal of Water Resources and Water Engineering, 2010, 21(2): 53-55. (in Chinese with English Abstract)

[17] Nash J E. The form of the instantaneous unit hydrograph[J]. International Association of Scientific Hydrology Bulletin, 1957, 45(3): 114-121.

[18] Andrew J, Guswa M A, Celia I, et al. Models of soil moisture dynamics in ecohydrology: A comparative approach[J]. Water Resources Research, 2002, 38(9): 1-15.

[19] 汪志农. 灌溉排水工程学[M]. 北京：中国农业出版社，2000.

[20] Allen R G, Pereira L S, Raes D, et al. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements[Z]. Rome: Food and Agriculture Organization of the United Nations. 1998.

[21] 芮孝芳. 水文学原理[M]. 北京：中国水利水电出版社，2004.

[22] 程东娟. 土壤物理实验指导[M]. 北京：中国水利水电出版社，2012.

[23] 张刘东. 石羊河流域灌区水资源管理与决策模型研究[D]. 北京：中国农业大学，2015.

Zhang Liudong. Water Resources Management and Decision-Making Model Research for Irrigation District in Shiyang River Basin[D]. Beijing: China Agricultural University, 2015. (in Chinese with English Abstract)

[24] 王浩，王建华，秦大庸，等. 基于二元水循环模式的水资源评价理论方法[J]. 水利学报，2006，37(12)：1496-1502.

Wang Hao, Wang Jianhua, Qin Dayong, et al. Theory and methodology of water resources assessment based on dualistic water cycle model[J]. Journal of Hydraulic Engineering, 2006, 37(12): 1496-1502. (in Chinese with English Abstract)

[25] Wang W K, Zhao J H, Duan L. Simulation of irrigation-induced groundwater recharge in an arid area of China[J]. Hydrogeology Journal, 2021, 299(2): 525-540.

[26] Lu X H, Jin M G, van Genuchten M, et al. Groundwater recharge at five representative sites in the Hebei plain, China[J]. Groundwater, 2011, 49(2): 286-294.

[27] Rossman N R, Zlotnik V A, Rowe C M, et al. Vadose zone lag time and potential 21st century climate change effects on spatially distributed groundwater recharge in the semi-arid Nebraska Sand Hills[J]. Journal of Hydrology, 2014, 519: 656-669.

[28] Fisher L H , Healy R W. Water movement within the unsaturated zone in four agricultural areas of the United States[J]. Journal of Environmental Quality, 2008, 37(3): 1051-1063.

Calculation method for irrigation return flow in a water diversion irrigation district of arid areas

Jie Feilong, Fei Liangjun※, Li Shan, Zhu Hongyan, Hao Kun, Liu Lihua

(,,710048,)

Many water diversion irrigation projects were launched in the arid areas of northwest China in recent years. Intense human activities have changed the water cycle of “diversion-irrigation-return” in the irrigation areas. In this study, the “Unit Return-Flow-Graph” was defined as the curve of irrigation return flow weight formed by deep percolation with uniform temporal and spatial distribution in a given watershed within a unit period. The Unit Return-Flow-Graph was then combined with the “Bucket model” (water balance model for crop root zone), thereby establishing the calculation model for the irrigation return flow. Deep percolation was also evaluated under the water balance, and then the Unit Return-Flow-Graph was combined to calculate the irrigation return flow. The study area was set as the Jingdian Irrigation District (part of the Yellow River Basin) in Gansu Province, China. The results showed that the calculated value of irrigation return flow in the study area fitted well with the monitored. The determination coefficient2in the model calibration and validation period were 0.82 and 0.71, respectively, indicating the reliable performance of the models. The validated model was used to calculate the deep percolation in the study area from 2000 to 2019 under the irrigation return flow from 2002 to 2019. The calculation results showed that the main influencing factor of yearly deep percolation was the sum amount of net irrigation and effective rainfall. The correlation coefficient between the sum amount of net irrigation and effective rainfall was 0.718 (<0.01), indicating a significantly positive correlation. The main influencing factor of monthly deep percolation was the crop growth period in the irrigation area, where 69.6% of deep percolation occurred during winter irrigation (October to November). A large amount of irrigation water and rainfall were consumed by crops in the form of evapotranspiration during the crop non-growth period, with less deep percolation. The coefficient of yearly deep percolation was significantly positively correlated with the yearly deep percolation (=0.944,<0.01). The monthly coefficient of deep percolation was significantly dependent on the crop growth. It was less than 0.4 in the crop growing period, but greater than 0.8 in the non-growing period. The reason was that the crop consumed more water during the growing period, but less for deep percolation. Low water consumption but more deep percolation occurred in the crop non-growing period. The main influencing factor was the yearly deep percolation, where the correlation coefficient between the two was 0.716 (<0.01), showing a significant positive correlation. The monthly irrigation return flow was correlated with the monthly deep percolation. The reason was that there was a significant lag time in the process of irrigation return flow. Since the curve was fitted to the Unit Return-Flow-Graph in the study area. The lagging peak of irrigation return flow was about 2 months, but the impact of deep percolation on the irrigation return flow reached about 24 months. The parameters of Unit Return-Flow-Graph presented clear physical meanings, relatively easy to determine the parameters using measured data. The Unit Return-Flow-Graph was effectively utilized to calculate the amount of irrigation return flow in water diversion irrigation areas, particularly on the water resources management in irrigation areas. In addition, the yearly and monthly deep percolation and irrigation return flow changed significantly, which affected the irrigation effect in Jingdian Irrigation District. The findings can provide a sound potential reference for water diversion in the irrigation districts of arid areas.

groundwater; infiltration; irrigation; water diversion; Unit Return-Flow-Graph; arid areas

介飞龙，费良军，李山，等. 干旱区引水灌区灌溉退水计算方法[J]. 农业工程学报，2021，37(13)：66-73. doi：10.11975/j.issn.1002-6819.2021.13.008 http://www.tcsae.org

Jie Feilong, Fei Liangjun, Li Shan, et al. Calculation method for irrigation return flow in a water diversion irrigation district of arid areas[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(13): 66-73. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.13.008 http://www.tcsae.org

2021-05-10

2021-06-10

国家自然科学基金资助项目（52079105，51779205）；甘肃省景泰川电力提灌灌区退（回归）水监测与利用研究项目（ZKGK-2016-023）；陕西省教育厅自然科学专项（16JK1539）；陕西省自然科学基础研究计划（2017JM5107）；西安理工大学博士学位论文创新基金（310-252072019）

介飞龙，博士生，研究方向为农业水资源利用。Email：jiefl@foxmail.com

费良军，博士，教授，研究方向为节水灌溉与农业水资源利用。Email：feiliangjun2008@163.com

10.11975/j.issn.1002-6819.2021.13.008

S27

A

1002-6819(2021)-13-0066-08