钢-混叠合梁非对称独塔斜拉桥风致响应性能研究

2021-09-15赵立轩

四川建筑 2021年4期

赵立轩

【摘要】为了研究钢-混叠合梁非对称独塔斜拉桥的抗风性能，文章以某主跨200 m的斜拉桥为背景，通过节段模型风洞试验测试了断面在成桥态和施工态下的颤振临界风速和颤振导数，采用三维颤振分析方法计算了断面的颤振临界风速，最后采用CQC抖振分析方法计算了该桥的抖振位移响应。结果表明：三维颤振分析与风洞试验得出的颤振临界风速均远大于颤振检验风速，表明桥梁具有良好的颤振稳定性;断面在成桥态和施工态下的抖振响应很小，且最大抖振位移对应的峰值加速度满足舒适度要求。

【关键词】钢-混叠合梁; 独塔斜拉桥; 颤振性能; 抖振响应; 风洞试验

【中国分类号】U448.27【文献标志码】A

独塔斜拉桥在经济，受力及施工等方面有着诸多优点，在斜拉桥中占有一定的比重[1]。钢-混叠合梁具有自重轻，受力性能好等优点，被广泛应用于斜拉桥的建设中[2-3]，然而，相比于流线型箱梁，叠合梁断面的气动性能较差，容易发生颤振、涡振等风致振动，在设计中应予以重视。

目前，关于钢-混叠合梁涡振性能方面的研究较多，段青松等[4]研究了不同风攻角下边箱叠合梁的涡振性能，发现断面在正攻角下易发生涡激振动，通过封闭部分栏桿能够降低涡振振幅;张天翼等[5]通过节段模型风洞试验研究了双边箱叠合梁的涡振性能，并对比了多种气动措施的制振效果，发现采用三角形风嘴和封闭栏杆结合的方式能够有效降低涡振振幅;雷永富等[6]采用全桥气弹模型风洞试验研究了武汉青山长江大桥在成桥态和最大单悬臂状态下的抖振性能，并参考现行抗风规范对桥梁的舒适性进行了评价。在大跨度桥梁断面的颤振临界风速识别方面，李加武等[7]在最小二乘法的基础上引入加权矩阵，提出了新的迭代方法，并通过节段模型风洞试验验证了该方法的可靠性;夏飞龙等[8]基于Scanlan颤振理论提出了一种显式颤振临界风速计算方法，该方法能够获得计算风速下的位移时程曲线，可以更直观地判断断面是否处于临界状态;张新军等[9-10]考虑了静风作用及风速空间分布等因素的影响，提出了一种三维精细化分析方法，使大跨度桥梁的颤振稳定性分析更加准确。在抖振性能方面，胡旭辉等[11]采用CQC法计算了某组合梁斜拉桥最大单悬臂状态下的抖振响应，并提出通过柔性拉索连接悬臂端的减振措施;向丹等[12]通过风洞试验研究了高宽比1∶6的矩形断面抖振力特性，发现断面的抖振阻力跨向相关性与跨向间距成反比;汪磊等[13]对比了实测风谱和规范风谱下某山区悬索桥的抖振响应，结果表明该加劲梁断面的抖振响应介于C类和D类场地之间，而桥塔的抖振响应值大于D类场地计算结果。

目前，关于非对称独塔斜拉桥抗风性能方面的研究较少，本文以某主跨200 m的非对称独塔斜拉桥为研究对象，通过节段模型风洞试验，并结合相关理论，对钢-混叠合梁的抗风性能展开研究，研究成果可为同类桥梁的抗风设计提供一定的参考。

1 工程概况

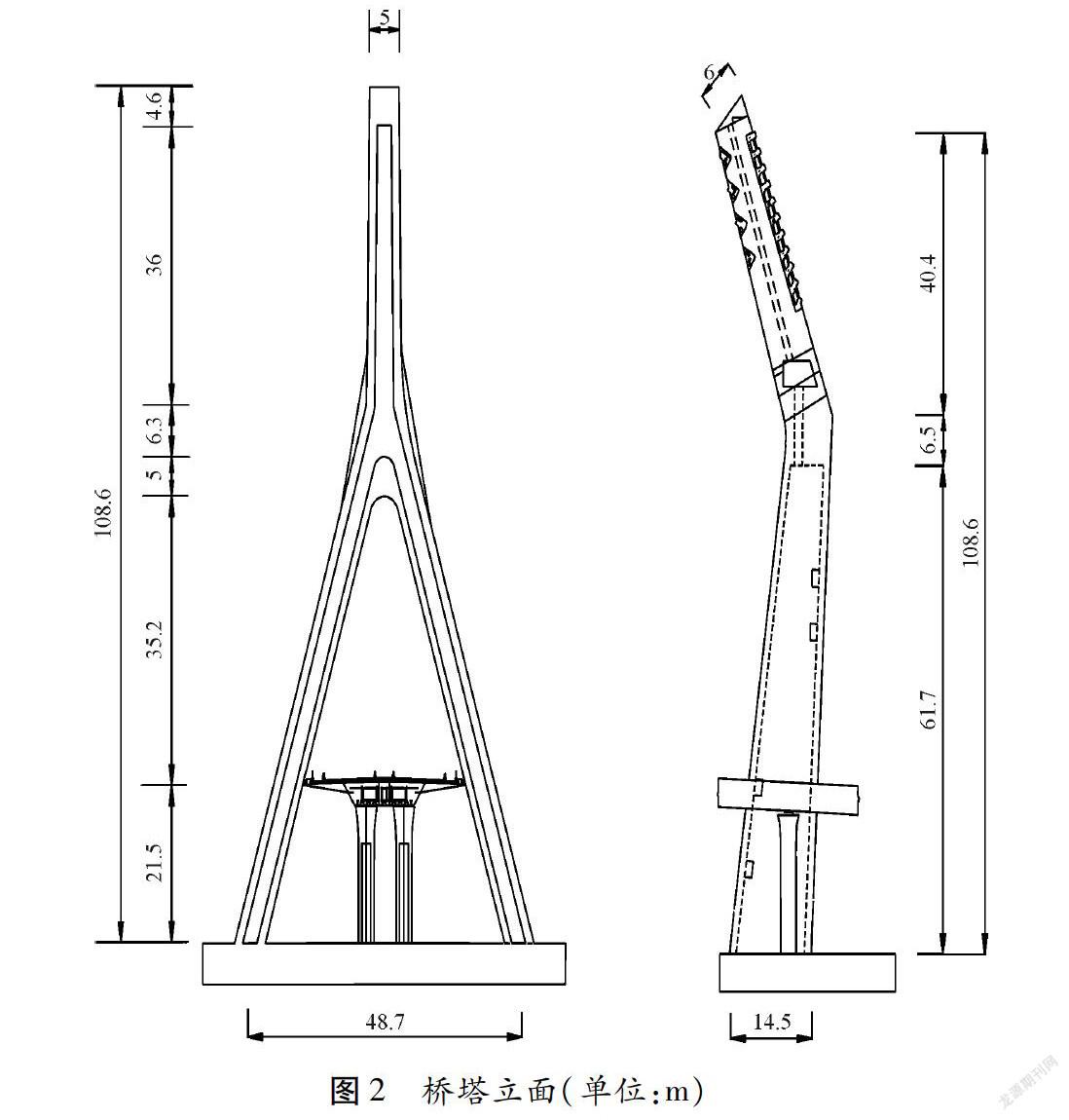
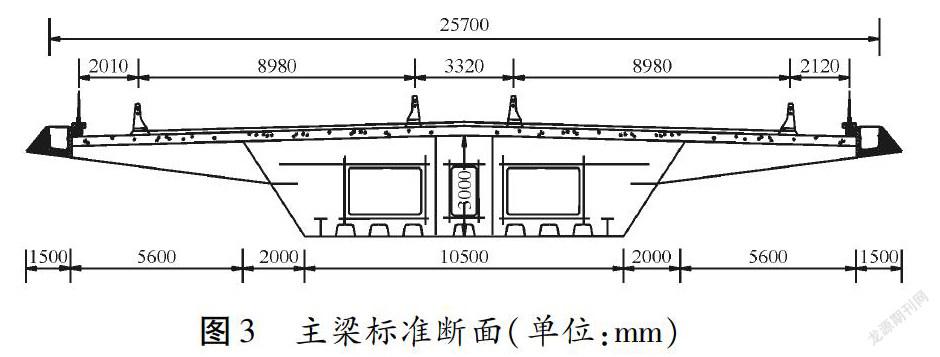
某独塔斜拉桥全长630 m，跨径布置为（24+38+53+3×65+200+2×60） m，如图1所示。其中主跨200m部分采用非对称独塔斜拉桥，主塔高108.6 m，采用人字形空间异形塔，如图2所示。主梁断面采用带挑臂的钢-混叠合梁，钢箱梁高3m，混凝土板厚0.25 m，桥面宽25.7 m，拉索采用单索面布置，如图3所示。根据当地风速资料，该桥设计风速为19 m/s，主梁颤振临界风速成桥状态为36.8 m/s，施工状态为28.7 m/s。

2 试验内容

试验在西南交通大学XNJD-1风洞第二试验段进行，该试验段长16.0 m，断面尺寸为2.4 m×2.0 m（宽×高），试验风速范围为0.5～45.0 m/s，均匀流场的紊流度<1.0 %，试验段有专门进行动力试验的装置。节段模型缩尺比取1∶50，模型的长、宽、高分别为2.095 m、0.574 m、0.065 m。主梁模型采用优质木材制成，人行道栏杆、防撞护栏和排水槽等附属构件采用工程塑料板制作，保证模型具有足够的刚度和精度。悬挂系统由8根弹簧和支架组成，能够为模型提供竖向和扭转二自由度运动，试验支架置于洞壁外，以免干扰流场。节段模型试验如图4所示。

3 主梁颤振性能

3.1 颤振临界风速

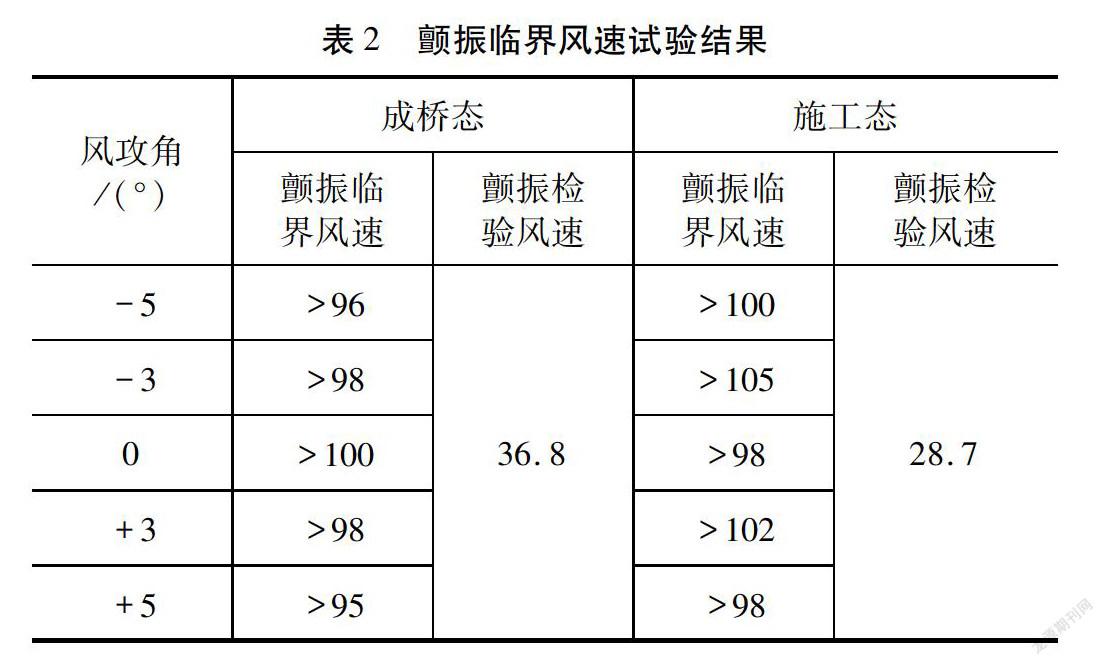
颤振稳定性试验在均匀流场中进行，其中成桥态下竖向阻尼比为0.33 %，扭转阻尼比为0.26 %，施工态（该桥采用顶推法施工，本文中的施工态均指100 %施工态）下竖向阻尼比为0.35 %，扭转阻尼比为0.27 %，节段模型的其余参数如表1所示。试验测试了成桥态和施工态下加劲梁断面的颤振临界风速，并通过风速比换算到实桥，试验结果如表2所示。

由表2可知，成桥态下断面的颤振临界风速均大于95 m/s，施工态下的颤振临界风速均大于98 m/s，远大于相应的颤振检验风速，表明该桥的颤振稳定性能较好。

3.2 主梁颤振导数

在桥梁颤振分析中，加劲梁断面运动引起的非定常气动力可以用气动导数来描述。根据Scanlan提出的气动自激力模型[14]，单位长度加劲梁断面上所受到的气动自激力的表达式如下：

式中：Lse、Mse分别为桥梁断面收到的升力和力矩;ρ为空气密度;U为来流风速;B为桥梁宽度;K=ωB/U为无量纲频率;Ai*、Hi*（i=1～4）是加劲梁断面的颤振导数;h、α分别为竖向和扭转位移。

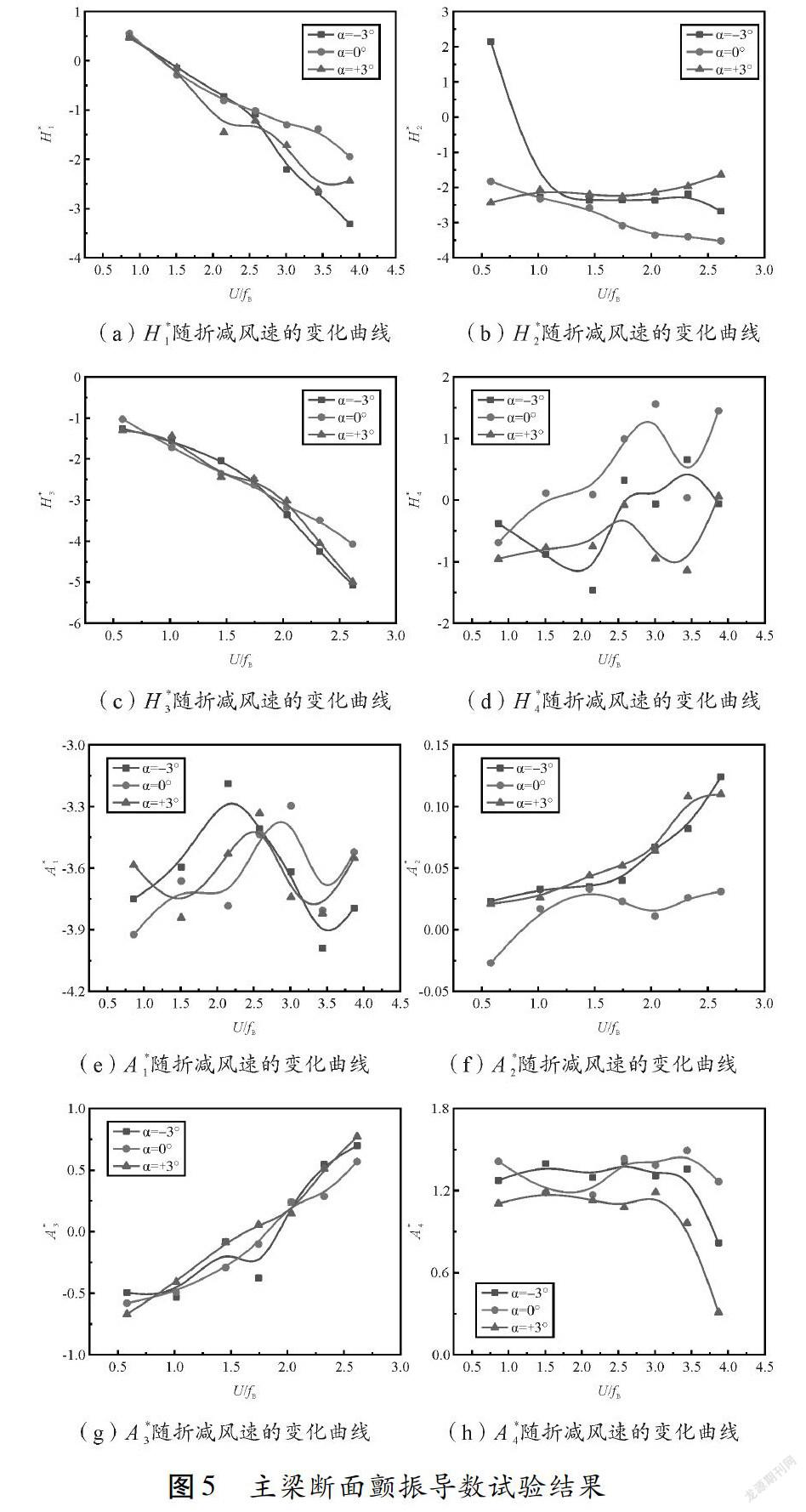
为了进一步考察加劲梁断面的颤振性能，利用风洞试验识别出了节段模型的颤振导数。图5列出了主梁断面-3 °、0 °、+3 °三个攻角下颤振导数与折算风速之间的关系曲线。

颤振导数可分为纯阻尼效应项H*1、A*2，纯刚度效应项A*3、H*4以及其余双重效应项[15]。对比不同攻角下的颤振导数发现，不同攻角下加劲梁断面的颤振导数存在差异，其中纯阻尼效应项H*1、纯刚度效应项A*3和双重效应项H*3在3个攻角下的颤振导数能够较好地吻合，而其余各项的差距较大，表明断面在各攻角下颤振临界风速的差异主要是由纯阻尼效应项A*2、纯刚度效应项H*4以及双重效应项A*1、H*2、A*4引起的。

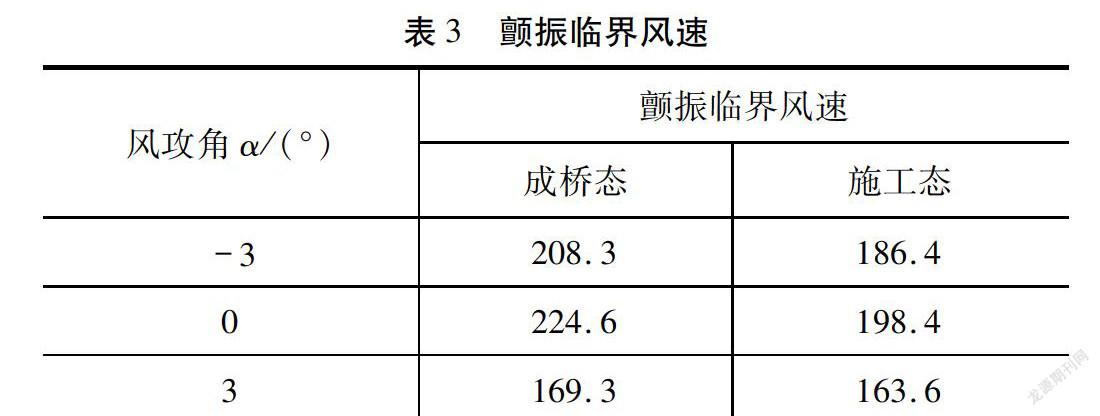
3.3 三维颤振稳定性分析

斜拉桥的振型通常是多个振型模态共同参与的结果，而节段模型试验只能模拟两个模态，为了更精确的评估桥梁的颤振性能，需要根据风洞试验得到的颤振导数，进行三维颤振分析，从而和节段模型的试验进行对比。根据三维颤振分析理论[10]，对斜拉桥进行三维颤振分析，计算结果如表3所示。从表中可以看出，三维颤振分析结果与风洞试验结果在定性上基本一致，成桥态和施工态下的颤振临界风速均远大于颤振检验风速，表明考虑了多模态后，颤振临界风速比节段模型更高。

4 抖振响应

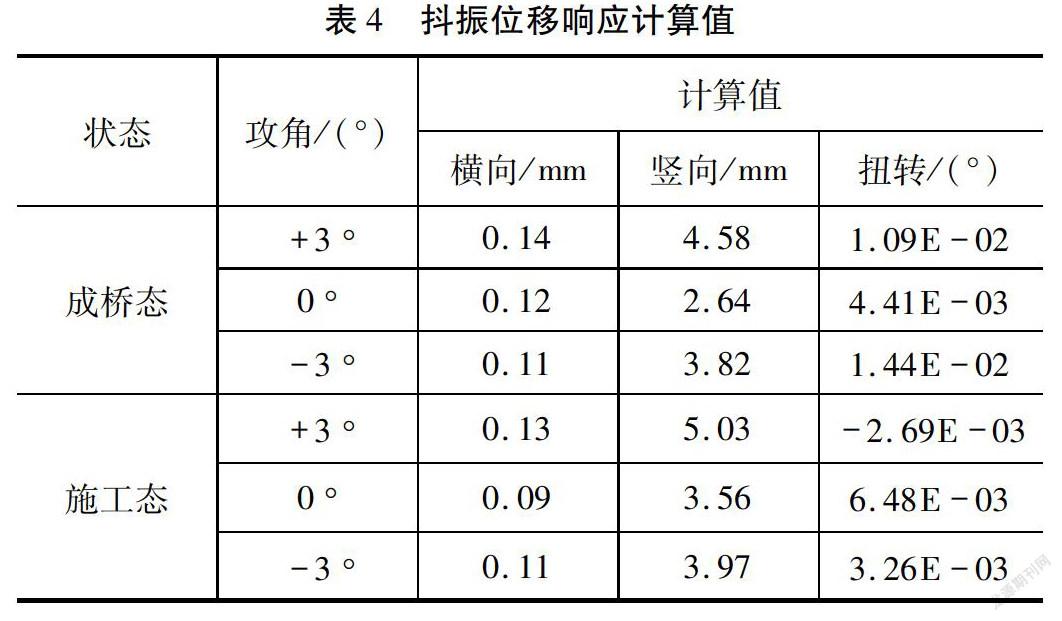
抖振是由自然风的脉动成分引起的随机振动。抖振一般不会造成桥梁的气动失稳，但其发生风速低、频率大，容易造成结构的疲劳破坏，过大的抖振位移还会影响行人和驾乘人员的舒适性。本文采用有限元CQC抖振分析方法对桥梁的抖振响应进行计算，该方法考虑了主梁断面和其他构件上的气动力，计算结果更准确。其中，对于脉动风谱的选取，纵向脉动风功率谱密度函数采用Kaimal谱，竖向脉动风速功率谱则采用Panofsky谱[16]。该桥在设计风速（19 m/s）下的抖振位移响应如表4所示。

关于风振舒适度的控制，规范[17]有如下规定，当风速不大于W1风作用水平时，有行人通行功能的桥梁抖振引起的竖向加速度峰值不宜大于1.1 m/s2，横向加速度峰值不宜大于0.5 m/s2。加速度与抖振响应之间的换算关系如式（2）所示：

ap=kpσi（x）（2πfi）2（2）

式中，kp为峰值因子，取3.5，σi（x）为桥梁x位置处第i阶振型抖振位移标准差（m），fi为第i阶振型频率（Hz）。

由表4可知，该桥横向位移和扭转位移几乎可以忽略，成桥态最大竖向仅4.58 mm，施工态最大竖向仅5.03 mm。按照式（2）计算成桥态和施工态在设计风速下对应的加速度分别为0.008 m/s2、0.010 m/s2，远小于规范限值，表明该桥的抖振性能良好。

5 结论

（1）风洞试验结果和三维颤振稳定性分析的结果显示，成桥态和施工态在不同风攻角下的颤振临界风速均远大于颤振检验风速，表明断面具有良好的颤振稳定性。

（2）成桥态断面在各攻角下颤振临界风速的差异主要是由纯阻尼效应项A2*、纯刚度效应项H4*以及部分双重效应项引起的。

（3）抖振响应的计算结果表明，该桥在成桥态和施工态下的抖振位移很小，最大抖振位移对应的加速度峰值满足规范对于舒适度的要求。

参考文献

[1] 杨征宇，宋桂峰，楼庄鸿.我国独塔斜拉桥[C]//中国公路学会桥梁和结构工程分会2006年全国桥梁学术会议.中国公路学会，2006.

[2] 董佳慧，周强，马汝为，等.边箱钢-混叠合梁颤振性能及气动措施研究[J].振动与冲击，2020，39（3）：155-160.

[3] 赵林，李珂，王昌将，等.大跨桥梁主梁风致稳定性被动气动控制措施综述[J].中国公路学报，2019，32（10）：34-48.