大跨钢桁梁悬索桥风致抖振响应时域分析
2021-09-15杨镇宇祝兵
杨镇宇 祝兵







【摘要】文章以飞龙湖乌江钢桁梁悬索桥为工程实例,基于主梁节段模型风洞试验测得静力三分力系数。按照实测风场特性,采用谱解法原理完成了脉动风谱到脉动风速时程的转换,基于小扰动假设条件下得到的准定常气动力理论求得桥梁结构时域化风荷载。采用ANSYS软件建立钢桁梁悬索桥的空间有限元模型并分析了桥梁结构的动力特性,进行了桥梁风致抖振响应时域分析。结果表明:该钢桁梁悬索桥在脉动风荷载作用下具有良好的抗风稳定性能。本研究思路及所得结果可以为该桥梁及其它类型悬索桥风致抖振分析及施工设计提供参考。
【关键词】钢桁梁悬索桥; 风洞试验; 风致抖振; 时域分析
【中国分类号】U441+.3【文献标志码】A
高速公路已经成为了我国经济社会发展的主动脉,进而出现了连接高速公路的主力军——大跨柔性桥梁。跨山区河谷地形的桥梁,由于桥位处地理条件相对比较复杂,此时,大跨悬索桥梁跨度大、重量轻、构造形式优美的优势便凸显了出来。钢桁梁主梁以其抗风性能优良以及架设安装易实现等优点,使其在大跨桥梁主梁中活跃度较高,大跨钢桁梁悬索桥受到了众多桥梁工程师的青睐[1]。但跨度大的同时也意味着桥梁柔性的增加,故其抗风性能评估也显得愈发重要。柔性桥梁在脉动风影响下易产生较大的抖振响应,影响行车安全和舒适性,长期会引发桥梁的疲劳,因而有必要对此类桥型开展抖振响应分析。桥梁抗风设计需要考虑的实际因素有很多,这些因素对悬索桥的设计计算有重要指导意义[4-6]。
本研究以飞龙湖乌江钢桁梁悬索桥为工程实例,基于ANSYS软件建立了悬索桥空间有限元模型,求解得到了钢桁梁悬索桥的结构动力特性。基于谱解法和准定常气动力理论得到作用于桥梁结构上的抖振风荷载时程,完成了大跨钢桁梁悬索桥在脉动风荷载下的抖振分析。
1 工程实例
1.1 工程概况
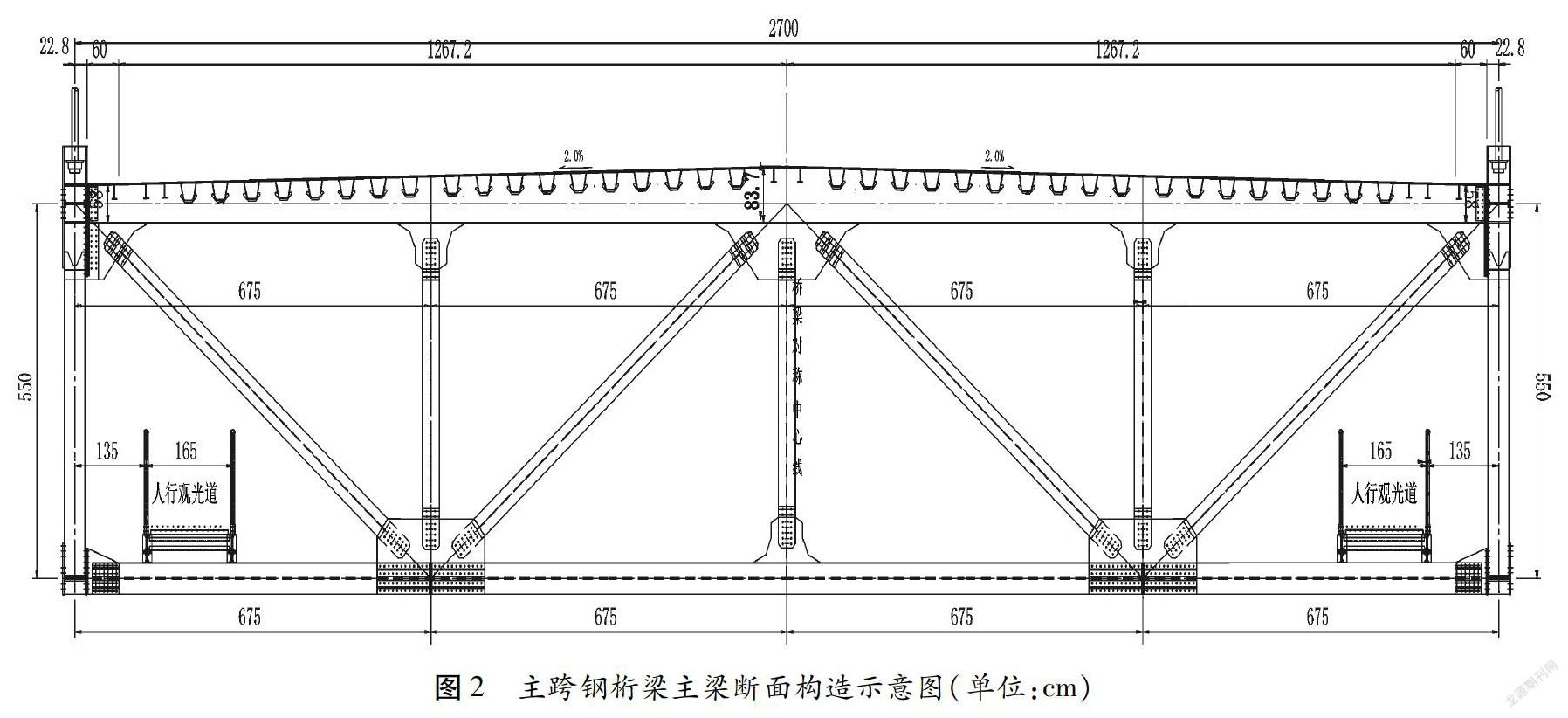
本文以飞龙湖乌江公路悬索桥为工程实例,大桥横跨乌江,孔跨布置情况为:(9×40+680+5×40) m,全长1 243.5 m,设计标准路幅宽度为24.5 m。大桥主跨主梁部分采用钢桁梁结构形式,主跨梁长为680 m,桥塔为门形框架形式。飞龙湖乌江钢桁梁悬索桥主跨布置形式如图1所示,主跨钢桁梁主梁断面构造示意图如图2所示。
根据JTG/T 3360-01-2018《公路桥梁抗风设计规范》[11],大桥所在区域为山区河谷地形,桥位处地表类别属于规范中的A类地表,地表粗糙度系数α0=0.12,桥址处地表粗糙高度z0=0.01 m,计算得出桥址处基本风速为U10=24.9 m/s,得到桥梁设计基本风速Us10=29.2 m/s。桥梁距离水面(地面)高度Z处的设计基准风速可按下式计算:
1.2 有限元模型
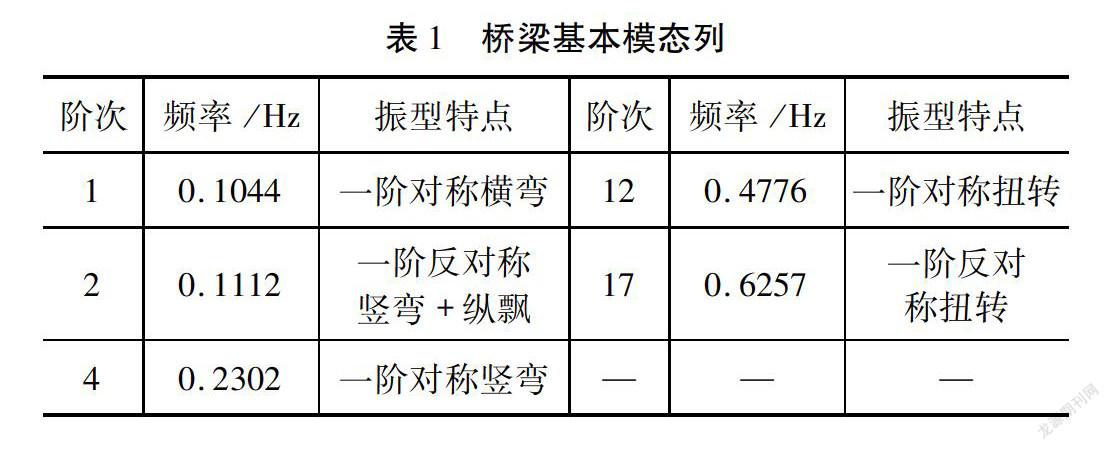
利用ANSYS软件建立了钢桁梁悬索桥整桥空间有限元模型,见图3。采用“鱼骨架”式建模方法,主梁和主塔均采用Beam44单元模拟,主缆和吊杆采用Link10单元进行模拟。对大桥成桥态进行了动力特性分析,得出桥梁基本模态如表1所示。
根据表1可以看出,主梁钢桁梁悬索桥第12阶振型出现了扭转模态,扭弯频率比为2.718。总结得出,该桥梁基频较高,且扭转模态出现的阶次较高,全桥抗风稳定性能良好。
2 桥梁风致抖振计算
2.1 主梁静力三分力试验
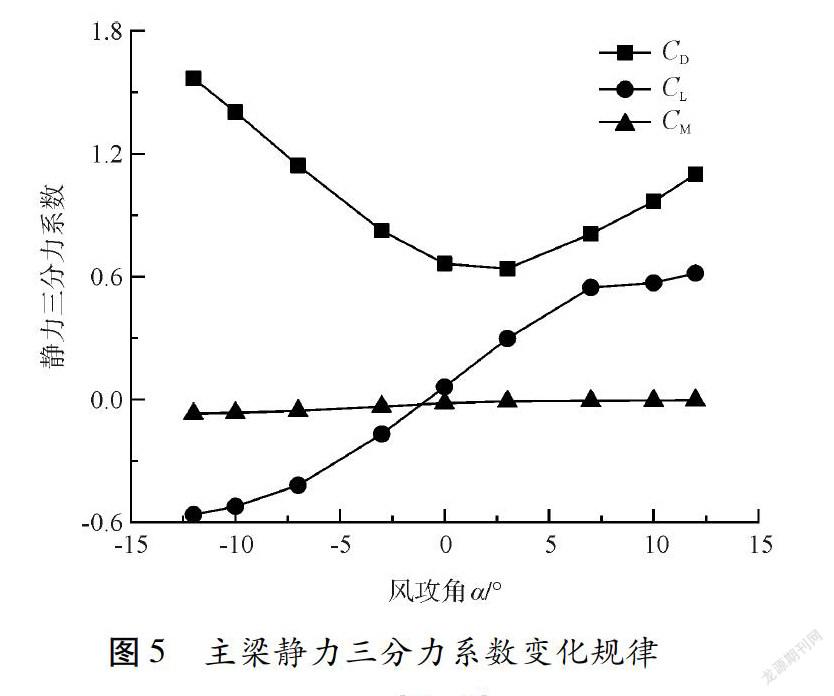
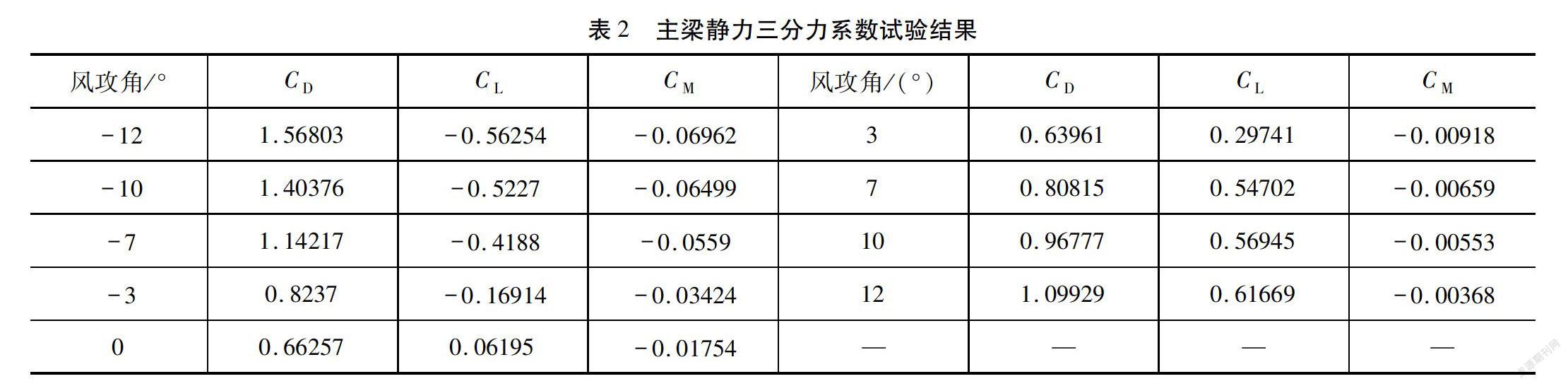
主梁节段模型风洞试验在位于西南交通大学的风洞实验室(XNJD-1)第二试验段中进行,采用成桥态主梁节段模型,几何缩尺比例为1∶41.23,实验室出风口的最大、最小来流风速分别为45 m/s、0.5 m/s。在主梁节段模型的前方放置有风速测试装置,风洞实验室内的成桥态钢桁梁主梁节段测力模型如图4所示。试验来流风攻角变化范围:α为-12~+12°,Δα=1°。试验来流分两种风速进行取为12 m/s和15 m/s,在两组数据接近的情况下,测试结果取二者的平均值。试验采集的数据结果包括体轴系和风轴系下的静力三分力。表2列出了風轴系下部分风攻角成桥态主梁静力三分力系数结果,图5为风轴系下主梁静力三分力系数随来流风攻角α变化规律图示。
2.2 脉动风速谱和力谱模拟[12-17]
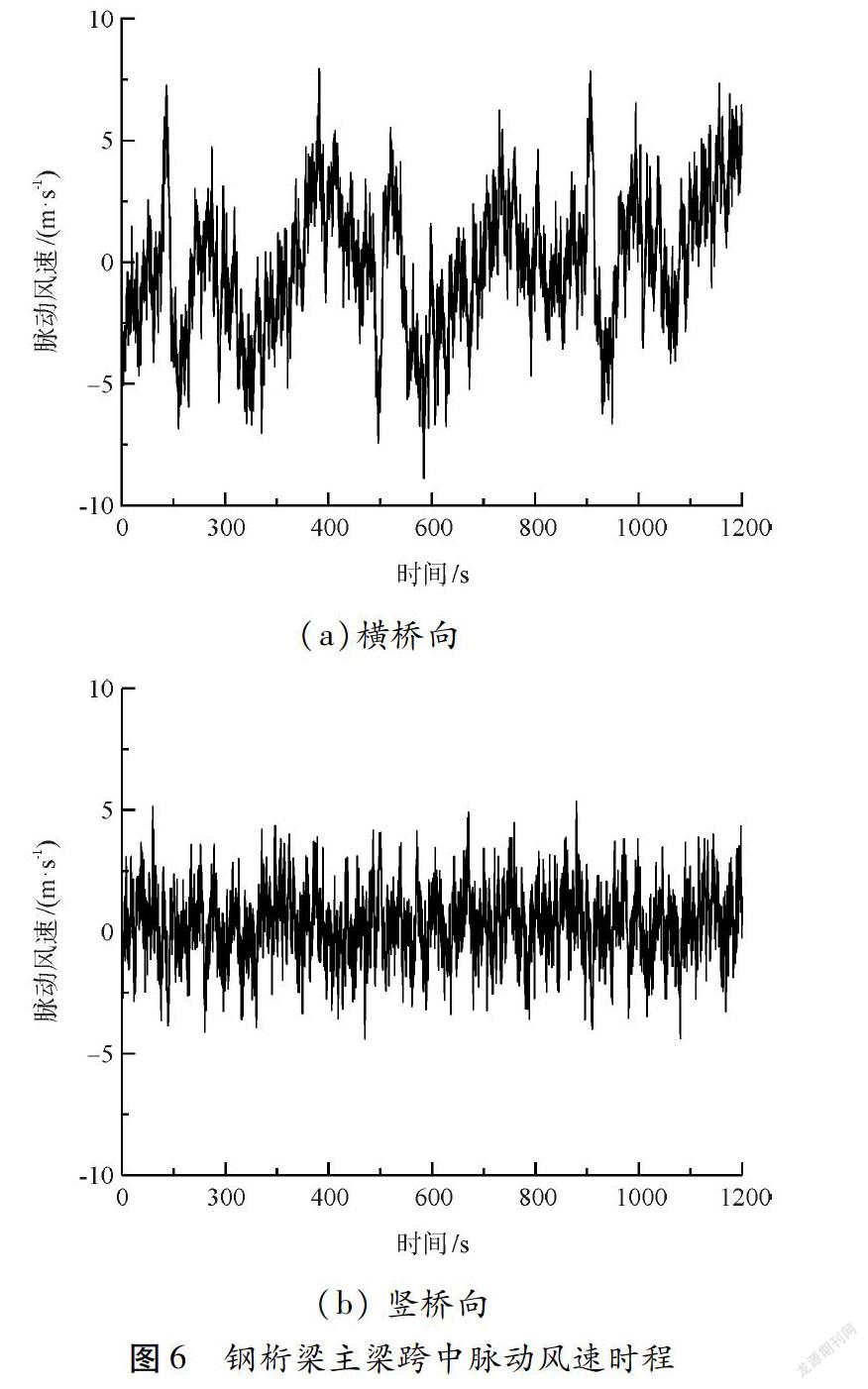
本研究采用的是新版JTG/T 3360-01-2018《公路桥梁抗风设计规范》[11]中推荐的脉动风速谱。基于谱解法采用MATLAB软件编程模拟脉动风速时程,模拟时选取主要参数包括截止频率为wu=5πrad/s,频率分割数N=1024,时间步长Δt=0.1s,采样时间点数M=4096。桥塔沿高度向的风速分布符合指数率分布。所得主梁高度处平均风速为31.0 m/s时成桥态主梁跨中横桥向、竖桥向脉动风速时程如图6所示。
本研究中气动导纳采用Sears函数考虑对全桥抖振的影响。基于小扰动状态下得到的准定常抖振力模型[18-19]实现
脉动风速时程向脉动风力时程的转换,并将所得静力风荷载和脉动风力时程施加到ANSYS中的有限元模型上,进行抖振响应时域分析[20-21]。
通常认为当来流风向与主梁桥跨正交时结构受力最为不利,本研究具体计算时主梁考虑所受的阻力、升力和力矩,而其他构件仅考虑阻力。飞龙湖乌江悬索桥典型成桥态风致抖振位移和内力计算分三部分进行考虑:一是不同风攻角下条件,包括0°和±3°;二是计算风速采用设计风速31.0 m/s;三是考虑自激力的作用。综合以上三点,乌江悬索桥抖振时程计算将分为3种工况,如表3所示。
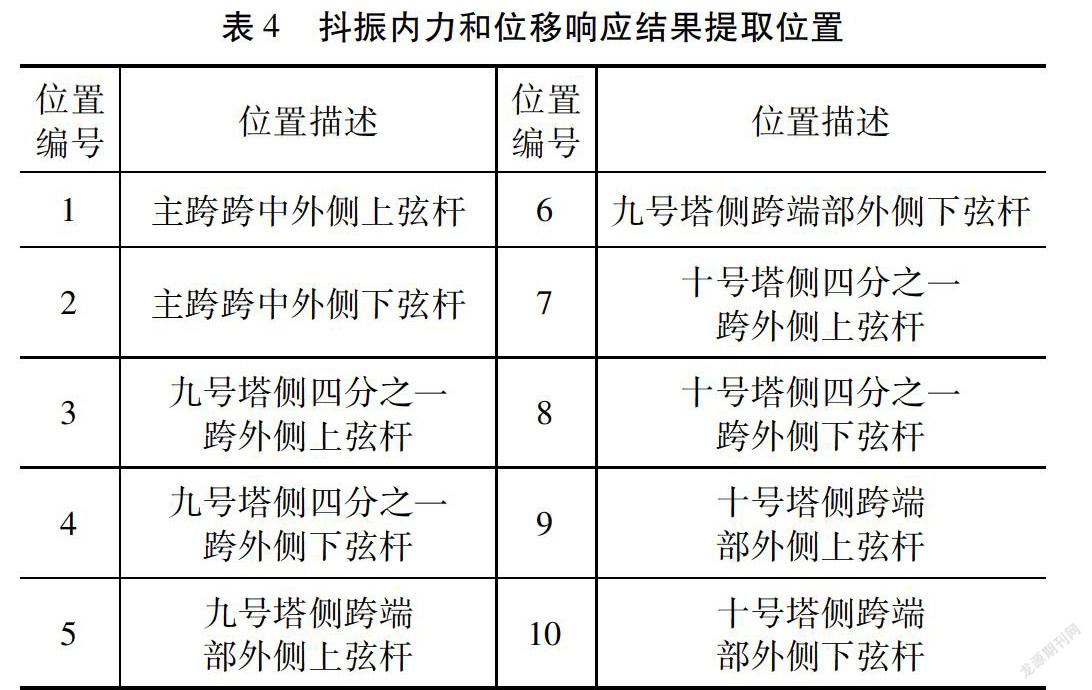
根据静风内力位移计算结果,主梁跨中风致内力和位移值最大,连接墩处风致横向弯矩最大。本算例暂不考虑主塔风阻力。不同工况下抖振内力和位移响应结果典型提取位置如表4所示,由于沿桥跨同一横断面位置处内、外两侧杆件抖振内力和位移值差异较小,表4仅以外侧杆件为例进行说明。
利用ANSYS软件计算时考虑了几何非线性、大变形及应力刚化的影响,计算总时长为600 s,时间步长取0.1 s。采用完全(Full)法收敛准则进行分析。结构阻尼通常会对振动产生较大影响,考虑到桥梁风致振动的特点,本算例采用的是瑞利(Rayleigh)阻尼输入。
3 抖振内力和位移响应结果
3.1 抖振內力响应结果
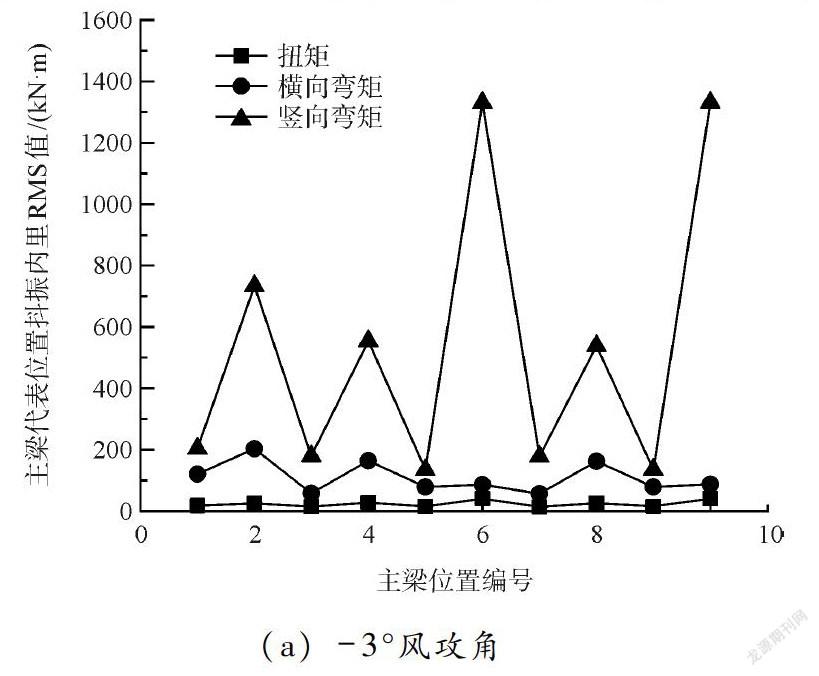
成桥态抖振内力响应计算时,取设计基准风速(31.0 m/s)作为抖振响应参考风速。成桥态部分风攻角下主梁典型位置处外侧杆件抖振内力响应结果如图7所示。
由图7可以看出,三种风攻角下主梁典型位置外侧杆件抖振内力响应RMS值及变化规律较接近。抖振内力响应以
图7 主梁典型位置处外侧杆件抖振内力响应RMS值(成桥态)-3 °风攻角时为最大,此时扭矩约为41.2 kN·m,横向弯矩约为232.9 kN·m,竖向弯矩约为1 340.8 kN·m。
3.2 抖振位移响应结果
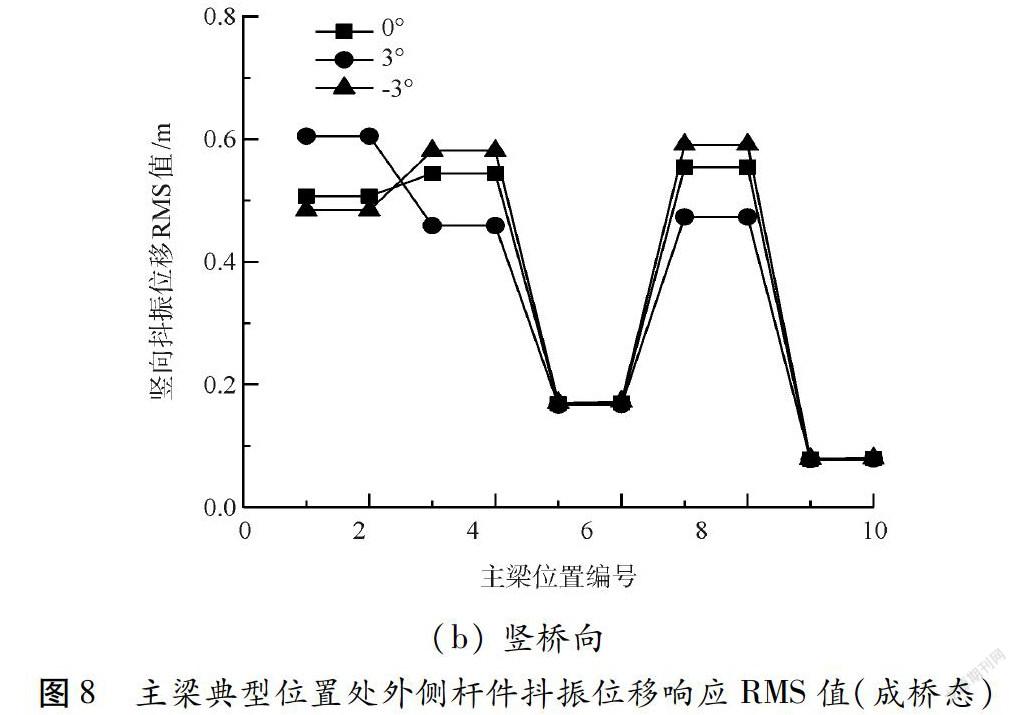
成桥态抖振位移响应计算时,取设计基准风速(31.0 m/s)作为抖振响应参考风速。三种风攻角下,成桥态主梁典型位置处外侧杆件竖向及横向抖振位移响应结果如图8所示。
由图8可以看出,三种风攻角下,主跨跨中位置处外侧上、下弦杆抖振位移响应表现为横向大于竖向,其余典型提取位置处的抖振位移响应整体上呈现出纵向略大于横向的规律。且横向和纵向位移响应均在主跨跨中位置附近达到最大值,其值略大于0.6 m。横向抖振位移最小约为0.17 m。
4 结论
通过钢桁梁主梁节段模型风洞试验及ANSYS软件中建立的空间有限元模型进行了大跨钢桁梁悬索桥风致抖振响应
时域分析,所得结论如下。
(1)总体而言,该桥基频较高,且扭转模态出现的阶次较高,抗风稳定性能良好。
(2)本算例给出了飞龙湖乌江悬索桥成桥态风致抖振内力响应值,可为相关设计提供借鉴。
(3)利用主梁节段模型风洞试验测试了静力三分力,采用MATLAB软件数值编程的方法完成了风谱向力谱的转换,最后通过ANSYS软件得出大跨钢桁梁悬索桥风致抖振内力和位移响应结果。本文采用的研究思路及所得结果可为其他大跨悬索桥风致抖振分析及施工设计提供参考。
参考文献
[1] 马存明,李丽,廖海黎,等. 特大跨钢桁梁悬索桥主梁气动参数试验研究[J]. 四川建筑科学研究,2010, 36(2):43-46.
[2] 贾巧燕,穆新盈,朱立军. 静风荷载作用下大跨度钢管混凝土拱桥位移的数值模拟[J]. 公路工程, 2019, 44(5):226-232.
[3] 黄浩. 风荷载作用下悬索桥受力分析与静风稳定性研究[J]. 公路工程,2019,44(4):98-102.
[4] 项海帆. 结构风工程研究的现状和展望[J].振动工程学报,1997,10(3):258-263.
[5] 刘高, 朱乐东, 项海帆.大跨悬索桥抖振内力响应分析[J].计算力学学报,2010,27(5):809-814.
[6] 马建, 孙守增, 杨琦,等.中国桥梁工程学术研究综述:2014[J].中国公路学报,2014,27(5):1-96.
[7] 韩兴, 黄博, 祝兵, 曾志文.基于谱分解法的自锚式悬索桥桥梁风致抖振计算分析[J].铁道标准设计, 2017, 61(9):82-86.
[8] 刘高, 林家浩, 王秀伟. 考虑全桥耦合的大跨斜拉桥抖振内力分析[J].大连理工大学学报,2003,43(4):479-483.
[9] 曹映泓, 项海帆, 周颖. 大跨度桥梁随机风场的模拟[J].土木工程学报,1998,31(3):72-79.
[10] 希埃米尔,罗伯特. 风对结构的作用[M].刘尚培, 项海帆, 谢霁明,译.2版.上海:同济大学出版社,1992.
[11] JTG/T 3360-01-2018 公路桥梁抗风设计规范[S].
[12] 苏成, 何滔. 崖门大桥施工阶段风致振动时域分析[J].桥梁建设,2003,33(1):69-73.
[13] 栗怀广. 钝体空气动力学的格子玻尔兹曼方法[D].成都:西南交通大学,2009.
[14] 李永乐, 廖海黎, 强士中.大跨度铁路斜拉桥非线性时域抖振分析[J].西南交通大学学报:自然科学版, 2004, 39(3):375-380.
[15] 李永乐, 廖海黎, 强士中.桥梁抖振时域和频域分析的一致性研究[J].工程力学, 2005,22(2):179-183.
[16] 李秋胜, 胡尚瑜, 李正农. 低矮房屋风荷载实测研究(Ⅱ)—双坡屋面风压特征分析[J].土木工程学报, 2012, 45(4):1-8.
[17] 李永乐, 周述华, 强士中. 大跨度桥梁三维脉动风场的模拟[J].土木工程学报,2003,36(10):60-65.
[18] R.H. Scanlan. The action of flexible bridge sunder wind. Ⅱ: buffeting theory. J. Sound and Vibration,1978,60(2):201-211.
[19] X.Z. Chen, M. Matsumoto, A. Kareem. Aerodynamic coupling effect son flutter and buffeting of bridges. J, Engng. Mech, 2000,126(1):17-26.
[20] Lin Y K. Motion of suspension bridge sin turbulent winds[J]. Journal of Engineering Mechanics, 1979, 105(ASCE15044).
[21] Li Y L, Liao H L, Qiang S Z. Weighting ensemble least-square method for flutter derivatives of bridge decks[J]. J. of Wind Engineering and Industrial Aerodynamics, 2003, 91(6):713-721.
