基于集成学习技术的隧道围岩智能分级方法研究
2021-09-15杜义康
杜义康






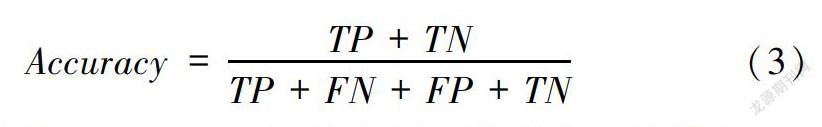

【摘要】隧道工程地质条件具有复杂多变的特点,造成围岩分级存在一定的模糊性。依托郑万高铁湖北段隧道工程,文章建立了不同级别不同岩性的随钻参数与围岩级别的数据库,研究了推进速度与其他随钻参数之间的相关性,建立了随钻参数与围岩级别的Stacking集成学习模型,增加了模型分类的稳定性,提高了模型预测准确度。该方法解决了传统隧道围岩分级方法存在评价方法单一、评价不及时、主观误差大等问题。
【关键词】隧道工程; 集成学习; 围岩分级
【中国分类号】U451+.2
【文献标志码】
A
隧道围岩级别是制定岩变我变、因岩施策的设计施工参数的主要依据。当前,研究隧道围岩分级方法主要分为间接方法和直接方法。其中,间接方法主要包括RQD方法、RMR方法、BQ方法。间接方法缺点是围岩信息采集往往需要地质人员到现场掌子面进行岩石取样与素描,存在人身安全风险。同时,现场测试岩体强度条件下需要手动输入少量指标参数代入经验公式,难以全面、准确地描述隧道围岩的性能与状态。
随着信息技术与计算机技术的进步,越来越多国内外研究者开始关注直接方法,即应用模糊数学[1-2]、高斯回归聚类[3]、相关系数[4]、人工智能[5]等技术,建立随钻参数与岩体之间的表征关系,快速评价隧道围岩质量,力求解决人为认知差异性问题。程士俊[1]研究应用专家系统实现围岩自动分级。Galende-Hernández, M [2]提出了应用模糊与机器学习结合的方法,建立了随钻参数与围岩级别的数学模型,快速评估隧道围岩质量。Navarro, J.[4]应用互相关方法,研究了随钻变量之间的相关关系,得到推进压力超前于其他随钻参数。邓洪亮[6]基于隧道监控量测数据,提出了围岩动态分级的修正公式。王琦[7]等基于能量分析法,推导了岩石单位切削能与随钻参数关系式,并依据试验结果建立了随钻参数与岩石单轴抗压强度的DP -UCS 模型。姚萌[8]研究了利用支持向量机方法建立随钻参数与围岩智能分级模型。
以上研究成果促进了隧道围岩分级进步,但是这些成果多数研究了单一随钻参数(或单一建模方法)与岩体性质映射关系,存在准确率偏低、模型泛化性能差的问题。当前,集成学习在数据建模与挖掘领域取得了非常好的效果,正逐渐成为研究的热点。结合国内外学者的研究,本文借鉴集成学习思想,提出将多个机器学习模型进行融合,通过取长补短的方式建立性能更优的集成学习模型,解决围岩级别预测准确率低、模型泛化性能差的难题。
1 项目背景
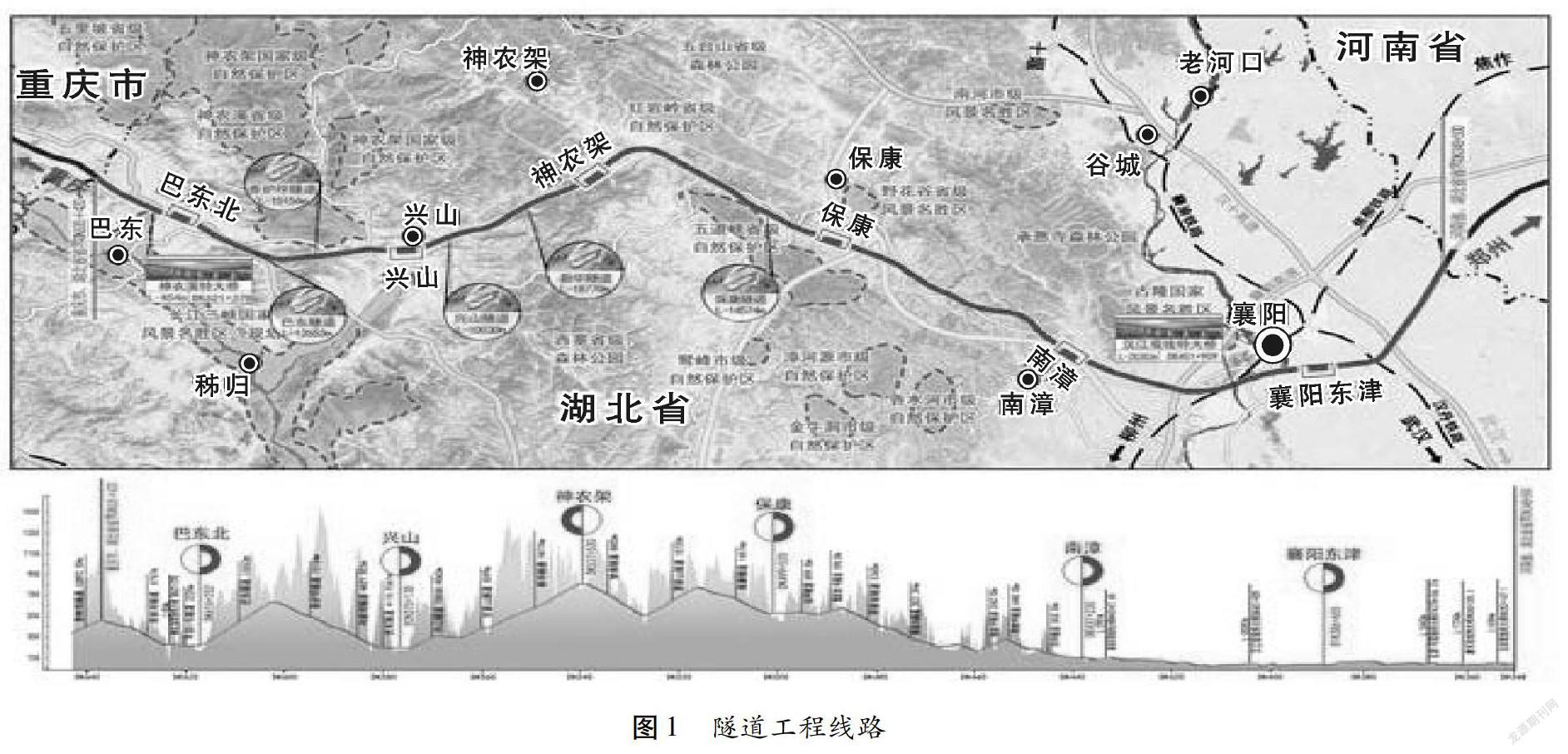
本项目主要依托郑万高铁湖北段隧道工程展开,隧道有32.5座,隧道总长167.619 km,占本段线路总长58.37 %。隧道开挖断面面积约150 m2,属于单洞双线大断面隧道,工程线路见图1所示。郑万高铁湖北段隧道II、III、IV、V级围岩主要涵盖页岩、灰岩、白云岩、砂岩、泥岩、变质砂岩、辉绿岩7种主要岩性,其中页岩、灰岩、白云岩、砂岩、泥岩5种岩性围岩地段长度占比88.8 %。目前,该隧道的多个标段均使用三臂凿岩台车进行掌子面开挖,应用凿岩台车构建的自感知系统,自动采集凿岩过程中的随钻参数,其作业现场如图2所示。
2 隧道围岩智能分级方法构建
2.1 数据样本库建立
本文建立的随钻参数与围岩级别样本库主要来自高家坪隧道、楚烽隧道、新华隧道、向家湾隧道、香炉坪隧道及安久铁路界子墩隧道等,涵盖白云岩、变质砂岩、灰岩、页岩、泥岩,主要包含III级、IV级、V级围岩,如表1所示。对于有监督机器学习分类问题,围岩级别标签正确性将影响围岩级别预测的准确性。依据JTG D70-2004《公路隧道設计规范》,本文采集了掌子面地质素描,并进行了岩石回弹、单轴饱和压缩强度、岩石波速、岩体波速等测试(图3~图5),验证现场地质工程师标注围岩级别标签的正确性,具体计算过程详见JTG D70-2004《公路隧道设计规范》。
2.2 相关性分析
凿岩机随钻参数包含推进速度、冲击压力、推进压力、回转压力、回转速度、水压力、水流量参数。其中,回转速度设置为恒定值,本文不考虑。一般情况下,推进速度一定程度上
反映了隧道围岩地质软弱。因此,应用Spearman方法分析推进速度与其他随钻参数的相关系数,获得参数之间相关性。表2表示参数相关性强弱。
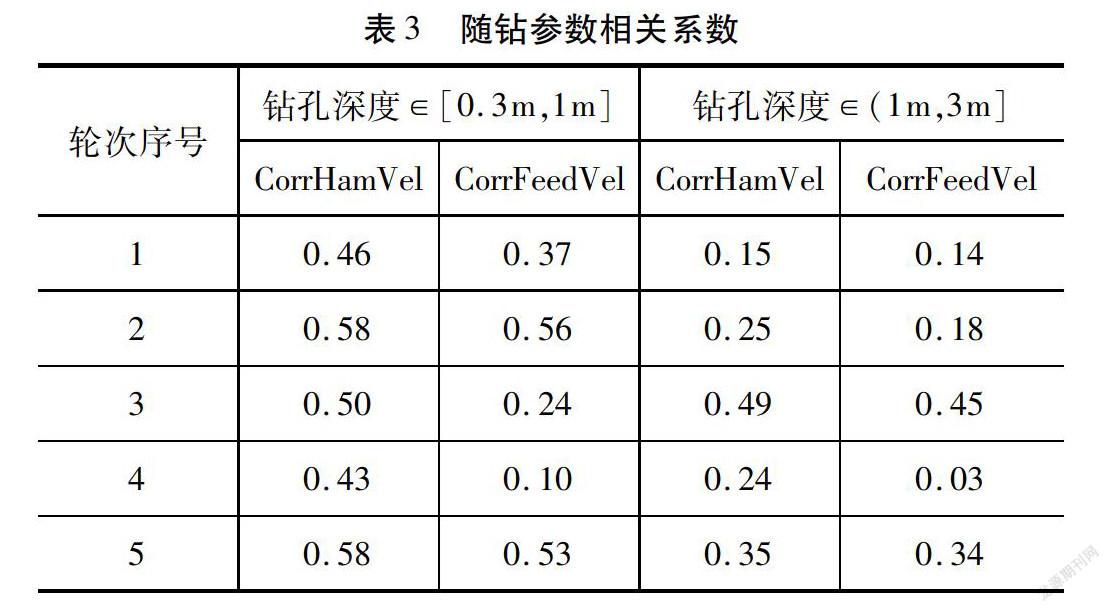
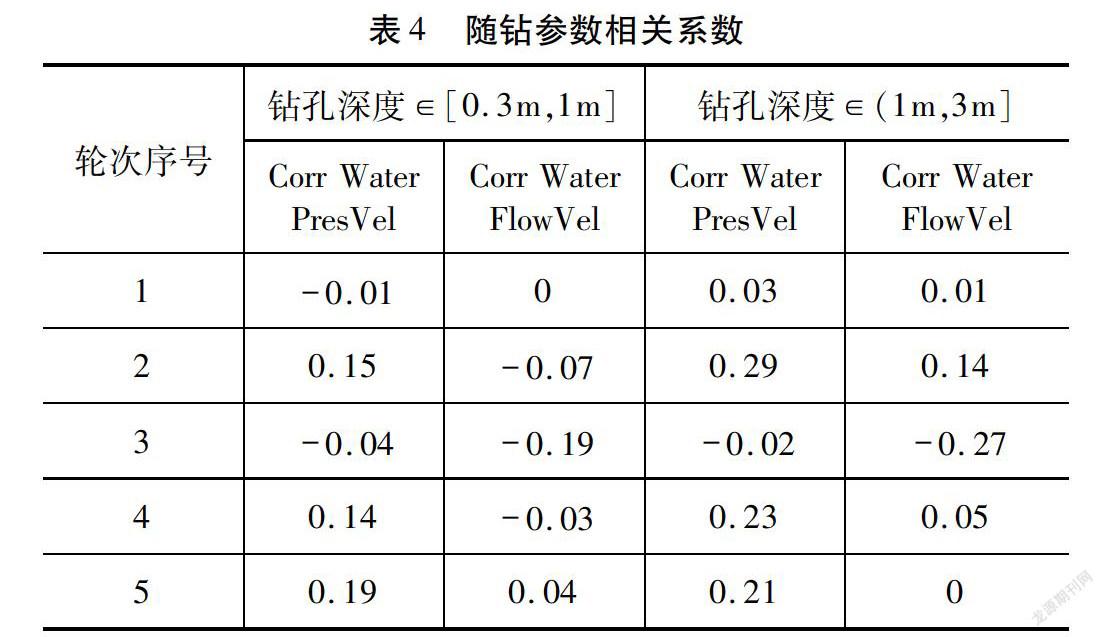
本文从随机选取多个隧道施工轮次下的随钻数据,由于篇幅限制,仅列出了5个轮次的计算结果。表3是冲击压力与推进速度、推进压力与推进速度的相关系数。从表3得到,冲击压力、推进压力均与推进速度呈现正相关,即增大冲击压力(或增大推进压力),增大推进速度。同时,发现轮次1~5的冲击压力与速度的相关系数大于推进压力与速度的相关系数。表4是水压力、水流量与推进速度的相关系数。从表4得到,水压力、水流量与钻孔速度相关系数最大值为0.29,大多数小于0.2,呈现弱相关性。因此,岩体状态参数与机电液设备参数之间存在一定相关关系。
2.3 数据预处理
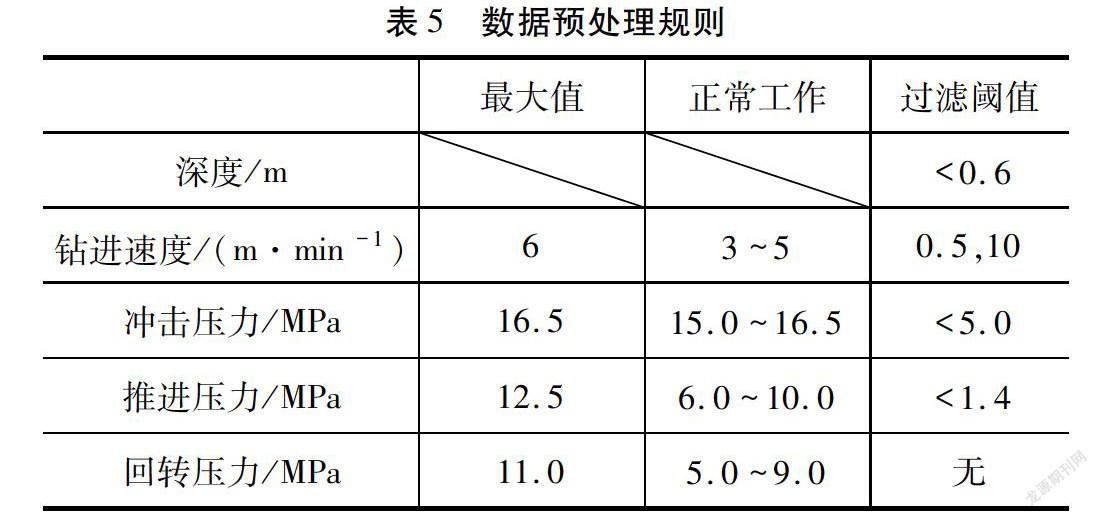
根据上文可知,深度、钻孔速度、回转压力、推进压力、冲击压力参数较重要。在此基础上,从能量转换角度,本文计算了定性判断隧道地层脆弱带特征的岩石钻进量,增大数据样本特征维度。针对凿岩机意外停机、回退等情况,本文提出了符合实际情况的数据预处理规则,如表5所示。同时,本文应用归一化方法对不同特征参数进行无量纲化处理,避免特征参数数据量级影响。
式中:de为钻进能量(J/cm3),He为打击能量(J),Ns为打击次数(bpm),le为损失系数,V为钻进速度(cm/min),Ap为孔隙剖面面积(cm2);
式中:Api为活塞受压面积,Sp为活塞行程,Hp为冲击压力。
由于不同隧道的施工进度有差异,隧道围岩级别数目不一致,存在类样本不平衡现象,导致分类器重视多数类而忽略少数类。为此,本文应用SMOTE(Synthetic Minority Oversampling Technique)方法处理不平衡数据分类方法,解决数据不平衡问题。其中,SMOTE随机过采样策略的原理与推导过程参考文献[9],本文不再赘述。
2.4 隧道围岩分级集成学习模型
机器学习方法可以有效解决统计回归模型难以处理的强非线性、高耦合性问题。支持向量机、随机森林、KNN等方法具有较强的非线性问题建模能力。然而,单一机器学习方法也存在泛化能力弱的缺点。因此,需要研究Stacking多模型融合的集成学习方法克服单个学习器泛化能力弱的缺点。
2.4.1 Stacking集成学习模型
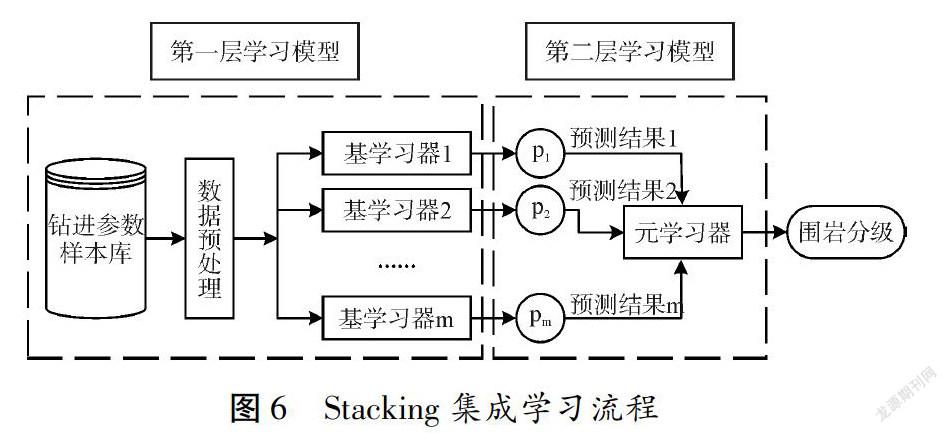
Stacking集成学习模型建立有两个步骤:一是基分类器选择与生成;二是组合策略选择。首先,预处理后的随钻数据集输入到第一层学习模型,即各个学习器,每个基学习器输出各自的预测结果;然后,将第一层输出结果作为第二层学习模型输入,对元学习器进行训练,再由元学习器输出最终预测的围岩级别,具体流程,如图6所示。本文将采用支持向量机、K近邻、随机森林算法作为基学习器以及线性回归算法作为元学习器,通过10折交叉验证方法对每个基学习器进行训练,训练完成后,对测试样本进行测试。
2.4.2 学习器基本原理
支持向量机算法是基于结构风险最小和VC维理论的传统机器学习方法,通过对训练样本构建一个最优分类超平面,达到各相对集中的训练样本与最优分类超平面的距离最远。该方法主要针对小样本数据进行学习、分类和预测,它有一个正则化项,有助于避免数据的过拟合,能够很好地处理非结构化和半结构化数据。由于类标签和特征之间的关系是非线性关系,本专题选择Gauss径向基核函数,可以将样本映射到一个更高维空间。
KNN(K-nearest neighbot)算法的核心思想是:每个数据样本都对应特征空间的1个点,如果在样本空间内1个距离当前未知类别数据样本最相邻的K个已知类别样本大多数属于某一个类别,则当前样本也属于这个类别[10]。KNN方法在类别决策时,主要依靠周围有限相邻样本,而不是依靠判别类域的方法来确定所属类别的。因此,对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
随机森林算法是使用分类回归树生成的决策树作为基分类器,在构建Bagging集成基础上,进一步在决策树的训练过程中引入了随机属性选择,依靠于决策树的投票选择来决定最后的分类结果[11]。该算法的特点能够处理具有高维特征的输入样本。
线性回归算法是应用多元线性公式解决回归问题,线性回归算法结构简单,原理易懂,同时又包含了机器学习算法的典型特征,是机器学习算法的典型代表[12]。
2.4.3 模型结果分析
2.4.3.1 分类模型评估指标
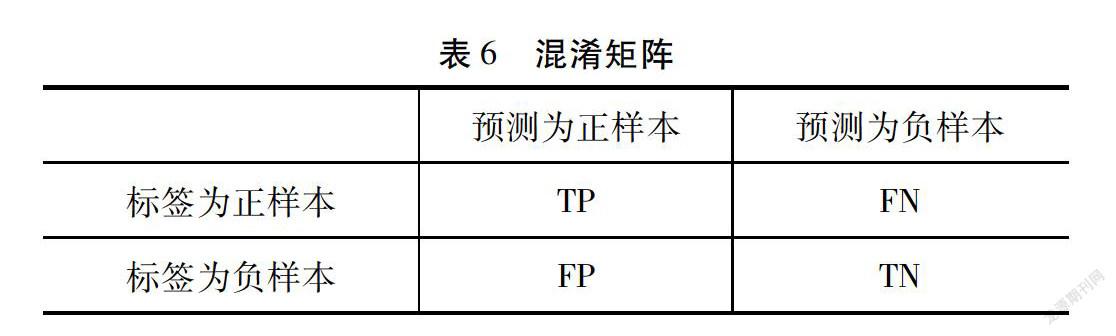
模型评估指标用于反映模型效果,需要将模型预测结果和真实标注进行比较。对于分类模型往往用混淆矩阵(表6)来进行效果评价,其中TP表示样本标签为正且模型预测结果也为正的样本数量,FP、FN和TN的含义类似,不再赘述。在混淆矩阵基础上,引申出精准率、召回率、F1-score多个评估指标,可以从不同角度来评价分类结果的优劣。为此,本文采用精准率、召回率、f1-score、准确率评估指标,全面评估KNN、SVM、RandomForest以及Stacking模型分类效果。各项评估指标定义及表达式如下所示:
(1)准确率(Accuracy):分类正确的样本占所有样本的比重,反映分类整体上正确率的评价。
(2)精确率(precision):在所有预测类别为正的样本中,模型预测正确的样本所占比重,反映分类器预测为某一个围岩级别正确率。
2.4.3.2 分类模型结果讨论
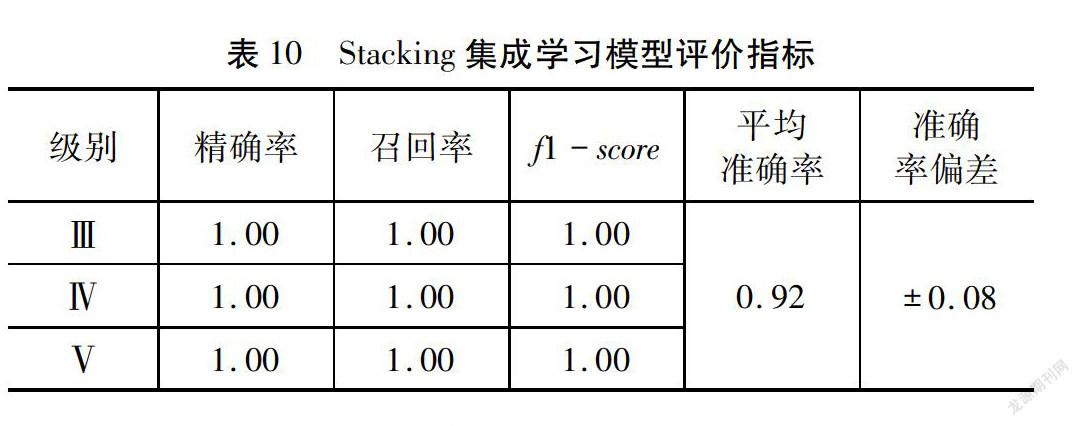
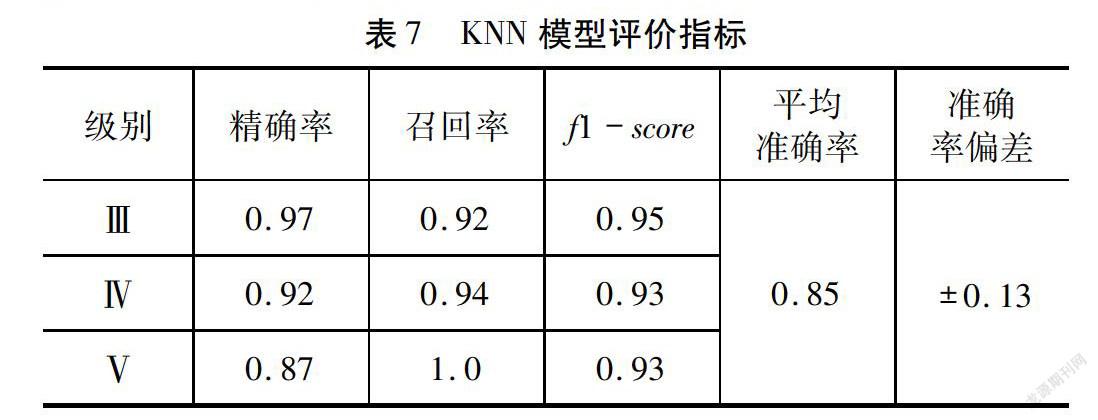
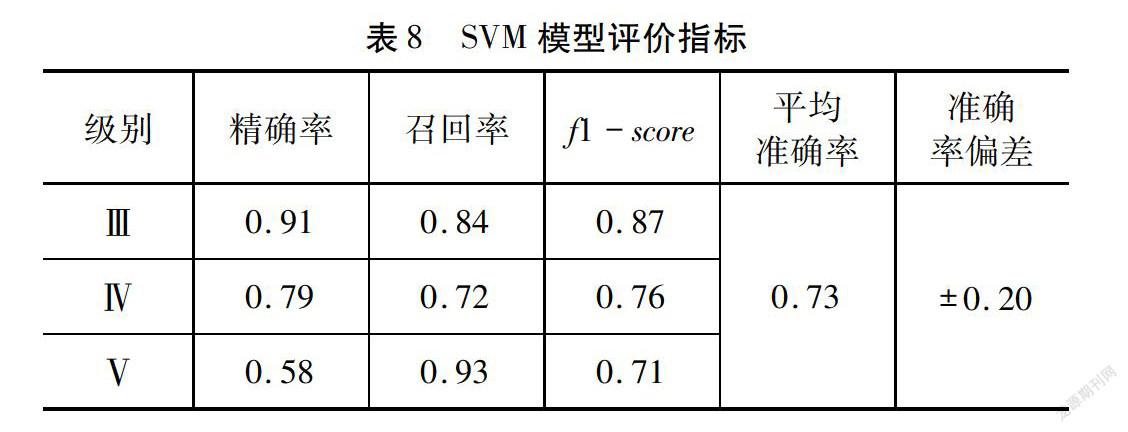
将交叉验证的测试集输入到训练好的模型,对围岩级别进行分类效果进行评估。本文采用精准率、召回率、f1-score、正确率指标全面评估单个分类器、集成分类器学习效果的优劣,计算结果如表7~表10所示。从表7~表10可知,在Ⅲ、Ⅳ、Ⅴ围岩条件下,RandomForest模型的精准率、召回率、f1-score、正确率指标均优于KNN模型以及SVM模型。Stacking集成学习模型的精准率、召回率、f1-score与RandomForest模型相当,但交叉平均准确率提高了4 %,达到了92 %,证明了本文模型准确性与有效性。
分级方法,通过分析得出以下结论:
(1)依托郑万高铁湖北段隧道工程,本文建立了III级、IV级、V级围岩条件下的随钻参数、围岩级别数据样本库,涵盖了白云岩、变质砂岩、灰岩、页岩、泥岩,为集成学习建模提供了数据基础。
(2)本文研究了定性反映地质软弱的推进速度与其他随钻参数相关性,确定了围岩分级特征参数。结合实际工况,确定了数据预处理规则以及不平衡类样本处理方法,解决数据“脏”与不平衡问题。
(3)本文建立了随钻参数与围岩级别的Stacking集成学习模型,增加了模型分类的稳定性,克服了模型预测准确度难以提高的问题,实现了预测准确率达到92 %。
后续工作:为了进一步提高隧道围岩智能分级方法的准确性,继续收集隧道施工现场随钻数据、地质数据,扩大数据样本库的围岩级别及数量。同时,由于随机误差的原因,收集的围岩级别样本中存在少数围岩级别標签不正确现象,须深入研究修正少数不正确围岩级别标签的建模方法。
致谢
本文的研究工作得到了湖南省创新型省份建设专项“超级地下工程智能成套装备关键技术研究与应用”经费资助(2019GK1010)、国铁集团科技研究开发计划“郑万高铁大断面隧道安全快速标准化修建关键技术研究”经费资助(2017G007-H),在此表示感谢!
参考文献
[1] 程士俊. 铁路隧道围岩分类专家系统[C]//第四届全国工程地质大会文集. 北京, 1992.
[2] Galende-Hernández M, Menéndez M, Fuente MJ,etal. Monitor-While-Drilling-based estimation of rock mass rating with computational intelligence: The case of tunnel excavation front[J]. Automation in Construction,2018, 93:325-38.
[3] Zhou H HP, Monteiro S T. Automatic Rock Recognition from Drilling Performance Data[C]// 2012 IEEE International Conference on IEEE.2012.
[4] Navarro J, Sanchidrian JA, Segarra P, etal. On the mutual relations of drill monitoring variables and the drill control system in tunneling operations[J]. Tunnelling & Underground Space Technology,2018, 72:294-304.
[5] Eskandarian S, Bahrami P, Kazemi P. A comprehensive data mining approach to estimate the rate of penetration: Application of neural network, rule based models and feature ranking[J]. Journal of Petroleum Science and Engineering,2017,156:605-15.
[6] 鄧洪亮, 周世生, 高文学,等. 基于监控量测的围岩分级修正方法研究[J]. 施工技术,2016,45:129-33.
[7] 王琦, 秦乾, 高松,等. 数字钻探随钻参数与岩石单轴抗压强度关系[J]. 煤炭学报,2018,43:1289-95.
[8] 姚萌. 基于钻进参数和SVM的围岩智能分级研究[J]. 四川建筑, 2020,40:149-51.
[9] Chawla NV, Bowyer KW, Hall LO, etal. SMOTE: Synthetic Minority Over-sampling Technique[J]. Journal of Artificial Intelligence Research, 2002,16:321-57.
[10] 闾城, 陈时熠, 华心果,等. 基于改进KNN算法的汽轮机通流故障诊断方法及应用[J]. 热力发电,2021,1-7.
[11] 李旭东, 方杰, 王培聪, 等. 基于随机森林的氧气-液氧掺混冷凝流型研究[J]. 武汉大学学报:工学版,2021,54:116-21.
[12] 董美娜, 刘丽平, 王泽忠,等. 基于Stacking集成学习的有源台区线损率评估方法[J]. 电测与仪表, 2021,1-7.
