以一道抛物线习题为例谈教学生成
2021-09-15谭新远
谭新远

[摘 要]在课堂教学中,教师善于抓住学生的思维闪光点,往往会有意想不到的教学生成.当学生向教师质疑问难,课堂上意想不到的事件会越来越多,这时教师一方面要顺应学生,因势利导,灵活处理;另一方面要不断反思.
[关键词]抛物线;课堂教学;教学生成
我校是一所农村学校,生源起点低,数学后进生较多,但我在课堂上尽量给予学生多点时间讨论、思考,充分发挥学生的主体性,同时也常开展小组合作学习,课堂气氛还是不错的,有时甚至可以说很热烈,并能带给我一些课堂意外的教学生成.有些教学生成令我印象深刻,特别是有一节抛物线的练习课案例.
一、课堂教学
课堂的预习学案中有这样一道题.
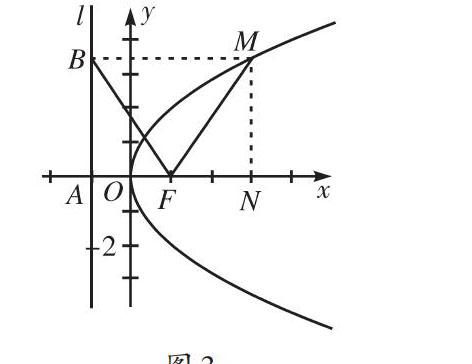
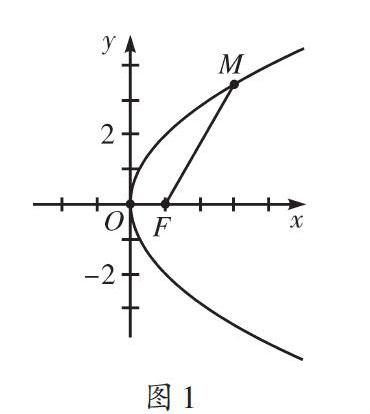
题目:如图1,M是抛物线上一点,点[F(1, 0)]是抛物线的焦点,以[Fx] 为始边、FM为终边的角[∠xFM=60°],求[FM].
备课时,我第一感觉就是求点M的坐标,可以借助直线方程与抛物线方程解方程组.教师教学用书,也是这样说明的.于是我将教学预设为解法一.
在教学过程中,我让学生练习思考3分钟后,开始提问.
教师:大家怎样解,答案是多少?
学生甲:等于4 .
我让他讲思路,他却讲了下面解法三(详见后面)的思路.
學生甲:先由点M向x轴引垂线,设垂足为N,利用已知条件,结合直角三角形MFN,可得[MF=2] [FN] ……(如图2)
教师:可以吗?
学生甲:可以的.
由于学生甲所讲的跟我的预设不一样,我还不太确定,且他答案正确,于是我叫他板书演示.
教师:还有不同的解法吗?
学生乙:可以先求直线FM的方程,求交点M的坐标.
教师:你求到了答案吗?
学生乙:求到了,等于4.
教师:也请乙同学来板书过程,其他同学可以自己思考和整理.
我在课堂巡视时又有新发现,学生丙利用焦半径求解,于是我和学生丙讨论完善.
教师:大家还有新的解法吗?
学生丙:可以把乙同学的过程简化一下,在求到[x=3]后,利用抛物线的焦半径公式[FM=d=x+p2=3+1=4].(就是后面的解法二)
教师:很好,计算更简便了.
二、教学后记
讲完这道题,时间已经过去二十分钟,我发觉远超预设时间.这就是我们经常讲的预设与生成的问题,课后想一想还是值得的.
备课中,预设是一节解法单一的习题评讲课,没想到学生反应如此热烈,小组讨论与交流也开展得有声有色,学生思维的火花得到碰撞,能力得到提高,更重要的是提高了学生学习数学的兴趣和信心,可谓一举多得.在推行素质教育的今天,强调学生自主学习,培养创新精神,鼓励独立思考,质疑问难,课堂上意想不到的事件会越来越多,怎样处理?我有以下的反思.
1.顺应学生,因势利导
所谓“智者千虑,必有一失”.尽管教师课前准备充分,但面对变化的课堂,往往会有一些意外发生.可出现意外并不是坏事,它恰恰反映了学生主动参与课堂活动的程度,至少表明部分学生的思维被充分激活.关键要看“意外”发生后教师的应变能力.
如何灵活处理“意外”事件显得尤为重要.它不仅关系着一堂课教学是否成功,而且是衡量一位教师教学机智的标志,反映出教师应变能力的水准.
在这节课中,学生的回答超出了教师的预设,导致教学要重新组织.这看起来似乎影响了教学进度,但提高了学生对于知识的灵活应用能力,这有利于培养学生的解题能力.
对于课堂“意外”,不要急于下结论,更不要急于否定,特别当教师还不能肯定对错时.应该给予学生思考的时间,因势利导,顺应学生的思维,教师再适时指导、适当提升.当学生提出不同解法或意见时,我觉得教师此时可用的一些引导语言有:你确定吗?你能具体一点写出来吗?让我们大家一起来思考一下吧;其他同学,你们认为可以吗?等等.
当然,你认为生成没有意义时,也应该及时引导学生向积极的方向思考,让其他学生来说或教师自己分析.不同情况有不同的处理方式,不能千篇一律.
课堂上很多的偶发事件是事先预料不到的,教师应该因势利导,随机应变,巧妙地把它融进自己的教学中,利用意外情况与讲授内容快速合理地结合,并借题发挥做文章.
2.不断反思,促进成长
要关注学生的成长,教师应该对教学进行反思;要促进自己的成长,教师更要对教学进行反思.反思能够发现教学中的不足,能够总结经验;反思是以往教学的总结,是后继教学的开端.
对于“意外课堂”,教师更要抓住机会反思,从而令以后的教学更有效.除了前面所提到的,笔者认为还可以反思很多内容.如:有更好的处理办法吗?下次我应怎样处理?专家可能会怎样处理?怎样教学更有效?等等.特别是要用文字记录一些课后反思,可以写在教案后面.经常反思,教师的能力一定会得到提升.
[ 参 考 文 献 ]
[1] 陶维林.从“把时间还给学生”说起[J].数学通讯,2011(14):1-4.
[2] 吴洁.对提升初中生数学课堂学习参与度的实践和思考 [J].考试周刊,2013(86):55.
[3] 严运华.提高数学课堂教学中学生的参与程度[J].教学与管理,1999(3):53-54.
[4] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2018:1-8.
[5] 钟进均.高中“说数学”案例研究 [M].广州:广东经济出版社,2017:240-260.
[6] 李祎. 数学教学生成论[M].北京:高等教育出版社,2008:12-15.
[7] 王同启. 一堂节外生枝的数学课[J].中学数学教学参考,2004(9):24-25.
(责任编辑 黄桂坚)
