单元关键课例确定与多维学习路径设计

方巧娟 汪芳

在“除数是一位数的除法”单元整体教学中，“一位数除两位数的除法笔算”是单元关键课例之一。我们针对不同学习起点，选择合适的学习材料，展开两条路径的学习，取得了较好的效果。我们发现，只要突破单元关键课例的教学，就能突破整个单元的教学。

一、单元关键课例确定

人教版数学教材三年级下册“除数是一位数的除法”单元，笔算教学序列主要从“一位数除两位数的除法”到“一位数除三位数的除法”，均包含首位能除尽和不能除尽的情况，后续补充有关0的除法。其中，“一位数除两位数的除法”的教学尤其困难，因为学生经验负迁移明显，认知扩展跨越大，主要体现在以下两点。

（一）竖式书写格式的负迁移多

从二年级的“有余数除法”笔算到“一位数除两位数的除法”笔算，时隔近一年之久，学生对笔算除法格式印象已模糊。另外，大部分学生受两位数除以一位数的口算及加法、减法、乘法竖式格式的干扰，容易将除法竖式写成加、减、乘的格式或者是“一层式”笔算格式，无法体验“两层式”笔算格式的优势。

（二）余数含义理解的认知扩展难

“除数是一位数的除法”笔算，主要解决两次及以上平均分物的过程与结果。竖式由“一层式”跨越到“多层式”，主要指向余数含义的扩展，体现在两个方面：首先，从原先的余几个一扩展到可以余几个一、几个十、几个百，余数对应的位置分别在个位、十位和百位;其次，随着余数产生的次数增多，会不断产生余数并继续分、该怎么分的问题。这个计算过程，可以看成有余数除法竖式不断循环的过程;不仅涉及除、乘、减多种运算，而且要解决余数的合并再继续除的问题，由此造成学生对余数继续分的认知具有一定的困难。

二、学情分析

（一）前测设计说明

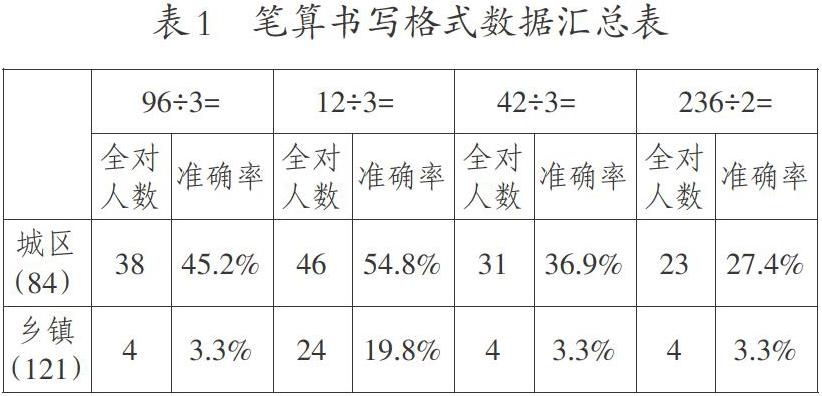
前测安排在学生学完“除数是一位数的口算除法”之后，抽样测查对象205名学生，其中城区学生84名，乡镇学生121名。前测题包括笔试、访谈两项内容。其中笔试内容为：笔算“96÷3”“12÷3”“42÷3”“236÷2”，画一画、写一写怎么计算“42÷2”和“34÷2”。访谈内容为：“42÷2”和“52÷2”是怎么算的？让学生用小棒来表示分的过程。

（二）测查数据分析

1.书写格式。

（1）原有经验对接不足。表内除法竖式遗忘较多，学生原有经验无法自主对接新知，主要错例集中如下：①加减乘笔算格式负迁移（如图1）;②了解除法竖式格式，但只写了被除数、除数和商（如图2）;③写了一层竖式（如图3）。

（2）城乡分化严重。受家庭教育和培训机构的影响，城区学生已经提前学会“除数是一位数的除法”的比例大大超过乡镇学生，学习起点差异大。

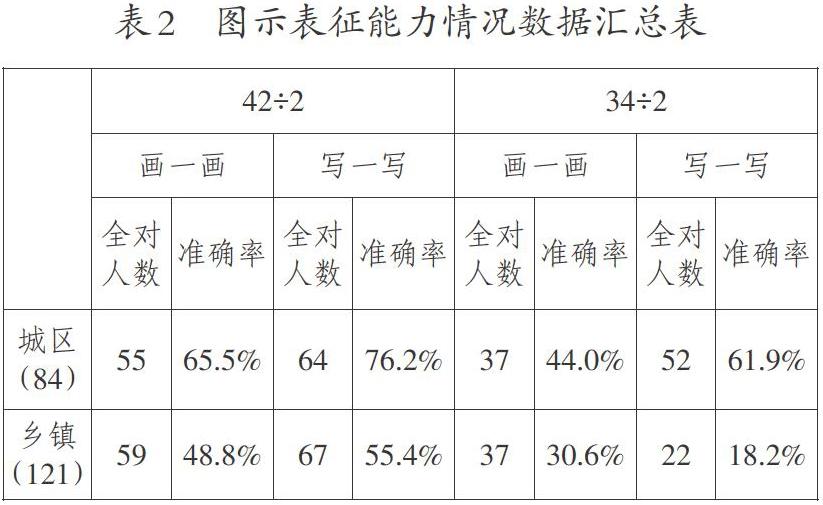
2.图示表征能力。

学生表征算式34÷2的图示表征困难更大，在课堂上教师要补充动手操作的实践活动，丰富学生的表象。

3.动作表征能力。

访谈中我们发现，给出小棒之后学生基本能完成平均分，但小棒拆分情况多样，其中42÷2分小棒过程主要指向先分整捆或者先分单根;52÷2分法则呈现“50+2”“40+10+2”“40+12”等多种分法。可见，学生分实物没有困难，但是两个算式均出现了多种分法，不利于创造与沟通笔算除法竖式。

三、路径优化与选择

由于学生的起点差异较大，我们选择合适的学习材料，确定了两条学习路径，供起点较低的学生和起点较高的学生选择。

（一）从有余数除法笔算到除数是一位数的除法笔算

课例设计特点：

分散难点，逐个突破，适合笔算格式遗忘较多、小棒拆分有困难的学生。学习路径从有余数除法笔算复习，扩展到除数是一位数的除法笔算。

目标导引：

1.通过唤醒学生原有知识技能，顺利迁移到一位数除两位数的笔算方法。

2.通过动手操作体验分后有余，需要通过拆分后继续分，凸显两次分的过程，并抽象成符号表征（包括横式表达与竖式表达）。

主要环节：

1.创设情境，复习回顾。

引出算式7÷2，借助小棒图理解有余数除法竖式7÷2的含义。

2.新课展开，探究竖式意义。

（1）引出70÷2，分小棒操作并讨论交流：第一次整捆分，第二次拆开后继续分。

（2）创造两次分的竖式，反馈学生作品进行优化与解读。

对比联系沟通：重点突破商的定位问题，两次分的竖式、横式、图示的对接以及经历十位有余拆分后继续分的过程。

3.跟进笔算72÷2和96÷3。

（1）跟进笔算72÷2，重点突破十位有余拆分和个位合并继续分。

（2）跟进笔算96÷3，迁移掌握十位除后无余的除法笔算格式。

（二）从十位除后有余到十位除后无余

课例设计特点：

聚焦难点、一次突破，适合学习起点较高的学生。学习路径从十位除后有余开始，把52÷2调整为42÷3，聚焦30+12小棒拆分与竖式的联系沟通。

目标导引：

（1）通过动手操作体验十位分后有余，和个位合并后继续分的过程，凸显两次分的过程，并完成符号表征（包括横式表达与竖式表达）。

（2）通过沟通竖式、横式和图示三者之间的联系，从而理解算理，掌握算法。

主要环节：

1.出示主例题引出42÷3。

2.小棒操作，架构算理，感悟算法。

（1）学生用小棒分一分。

（2）反馈交流。

根据学生反馈说清楚两次分小棒的过程，并理解为什么整捆开始分。

（3）结合分的过程创造两次分的竖式格式。

（4）沟通联系，结合图4理解两次分的竖式格式。

①先分了什么？（3捆）竖式中怎么体现？

②每份分到多少？（每份1捆）怎么写商？

③分掉了多少？（分了3捆）又是怎么算的？

④還剩下多少？（剩下1捆）

⑤那接下去算什么？12怎么来的？

把个位上的2落下来与十位上的1合起来，变成12继续分。

3.补充42÷2的学习。

（1）补充情境引出算式42÷2。

（2）通过迁移确定小棒的分法，明确竖式从高位算起的方法和图示联系。

（3）对比交流：比较42÷2和42÷3计算上的异同。

四、后测分析

后测选取了城区同等水平的两个班级学生，共80人，分两条路径学习，针对运算正确与算理理解跟进后测分析，情况如下。

1.运算正确：笔算格式书写规范较好，路径一掌握情况略优于路径二。

从数据看，两条路径学生的运算能力均有了大幅度提升，但路径一重难点分散，知识点循序渐进，所以学生笔算格式掌握情况要略优于路径二。其次，256÷2考查学生的迁移能力，两个班均有半数以上学生会迁移。

2.算理表征：画图表征能力提升明显，路径二拆分正确略高于路径一。

从理解算理维度的“34÷2”画图表征数据看，路径一会正确拆分的人数略低于路径二。主要原因是路径二集中了教学难点，在主例题讲解时一次性突破了十位余后拆分与个位合并的过程;而路径一主例题只讲解了分后有余拆分后继续分的过程，对拆分合并过程只是在后续尝试练习中进行了补充。

总体来看，两条学习路径都实现了优化，但路径不同，能力提升的维度也有所不同。路径一注重竖式格式规范的循序渐进，在运算正确上略胜一筹;路径二聚焦重难点让学生创造竖式，突破了竖式为什么要从高位算起，理解了十位余后拆分与个位合并继续分的过程，在算理理解上更加深刻。可见，如果学生起点较低，可以选择路径一，在运算正确上做好保底;如果学生起点较高，可以选择路径二，让学生自主创造，加深算理和算法的融通。

（作者单位：浙江省宁波市奉化区江口街道中心小学 浙江省宁波市奉化区龙津实验学校）